Bruno Gonçalves, profile picture
Uploaded byBruno Gonçalves
PDF, PPTX1,039 views

RNNs for Timeseries Analysis

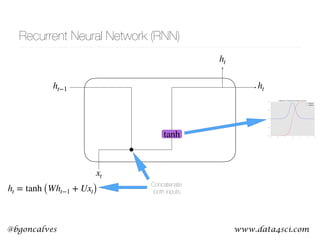
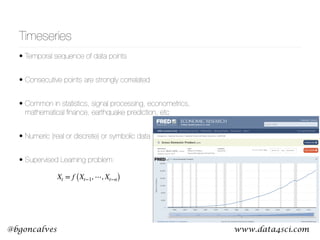
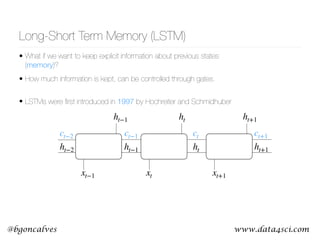
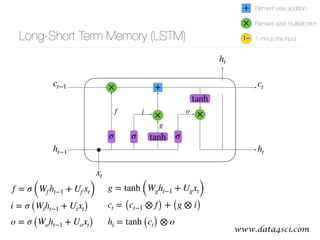
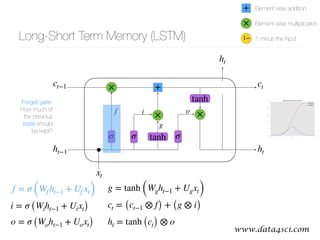
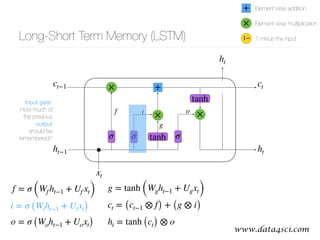
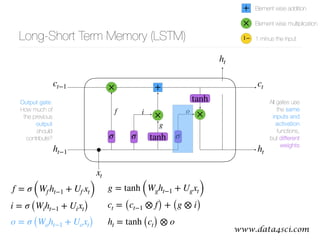
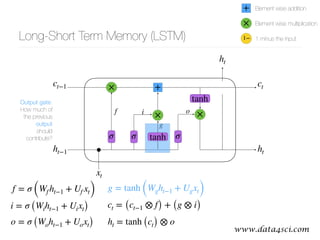
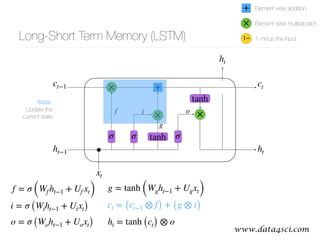
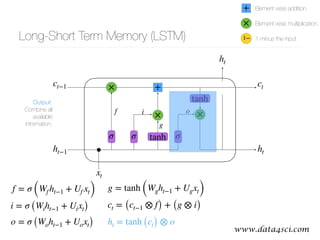
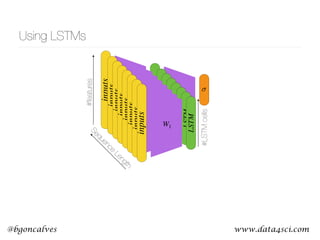
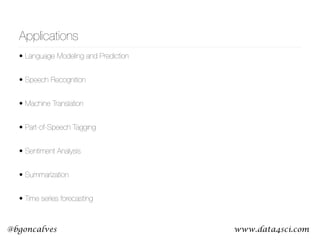
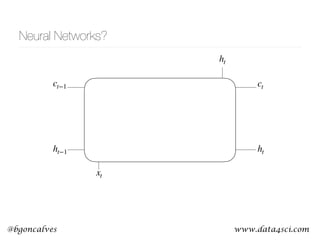
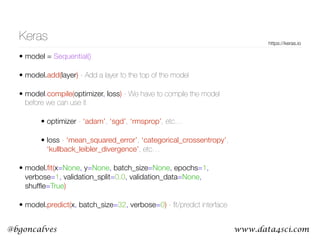
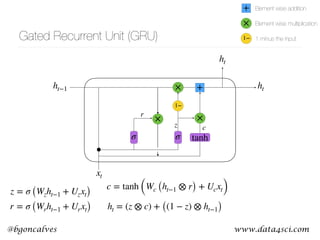
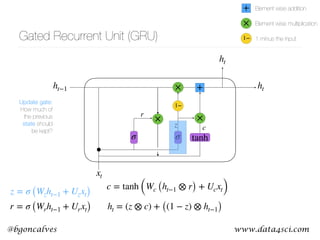
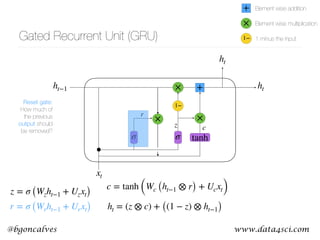
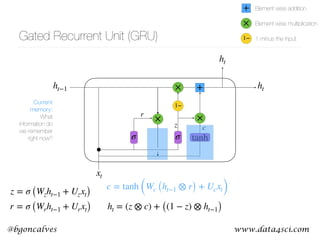
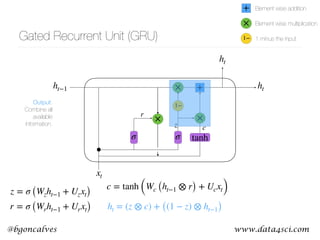
This document presents a comprehensive overview of recurrent neural networks (RNNs) and their applications in time series analysis, including fundamental concepts such as feedforward networks, backpropagation, and long short-term memory (LSTM) architectures. It discusses the optimization problems involved in machine learning, introduces gated recurrent units (GRUs) as a simplified alternative to LSTMs, and highlights the use of Keras for building neural network models. Practical applications of these techniques span various fields, including language modeling, speech recognition, and time series forecasting.

Embed presentation

Download as PDF, PPTX
RNNs for Timeseries Analysis 
 www.data4sci.com github.com/DataForScience/RNN
www.data4sci.com@bgoncalves The views and opinions expressed in this tutorial are those of the authors and do not necessarily reflect the official policy or position of my employer. The examples provided with this tutorial were chosen for their didactic value and are not mean to be representative of my day to day work. Disclaimer
www.data4sci.com@bgoncalves References
www.data4sci.com@bgoncalves How the Brain “Works” (Cartoon version)
www.data4sci.com@bgoncalves How the Brain “Works” (Cartoon version) • Each neuron receives input from other neurons • 1011 neurons, each with with 104 weights • Weights can be positive or negative • Weights adapt during the learning process • “neurons that fire together wire together” (Hebb) • Different areas perform different functions using same structure (Modularity)
www.data4sci.com@bgoncalves How the Brain “Works” (Cartoon version) Inputs Outputf(Inputs)
www.data4sci.com@bgoncalves Optimization Problem • (Machine) Learning can be thought of as an optimization problem. • Optimization Problems have 3 distinct pieces: • The constraints • The function to optimize • The optimization algorithm. Neural Network Prediction Error Gradient Descent
www.data4sci.com@bgoncalves Artificial Neuron x1 x2 x3 xN w 1j w2j w3j wN j zj wT x aj (z) w 0j 1 Inputs Weights Output Activation function Bias
www.data4sci.com@bgoncalves Activation Function - Sigmoid (z) = 1 1 + e z • Non-Linear function • Differentiable • non-decreasing • Compute new sets of features • Each layer builds up a more abstract
 representation of the data • Perhaps the most common http://github.com/bmtgoncalves/Neural-Networks
www.data4sci.com@bgoncalves Activation Function - tanh (z) = ez e z ez + e z • Non-Linear function • Differentiable • non-decreasing • Compute new sets of features • Each layer builds up a more abstract
 representation of the data http://github.com/bmtgoncalves/Neural-Networks
www.data4sci.com@bgoncalves Forward Propagation • The output of a perceptron is determined by a sequence of steps: • obtain the inputs • multiply the inputs by the respective weights • calculate output using the activation function • To create a multi-layer perceptron, you can simply use the output of one layer as the input to the next one.
 x1 x2 x3 xN w 1j w2j w3j wN j aj w 0j 1 wT x 1 w 0k w 1k w2k w3k wNk ak wT a a1 a2 aN
www.data4sci.com@bgoncalves Backward Propagation of Errors (BackProp) • BackProp operates in two phases: • Forward propagate the inputs and calculate the deltas • Update the weights • The error at the output is a weighted average difference between predicted output and the observed one. • For inner layers there is no “real output”!
www.data4sci.com@bgoncalves The Cross Entropy is complementary to sigmoid activation in the output layer and improves its stability. Loss Functions • For learning to occur, we must quantify how far off we are from the desired output. There are two common ways of doing this: • Quadratic error function: • Cross Entropy E = 1 N X n |yn an| 2 J = 1 N X n h yT n log an + (1 yn) T log (1 an) i
www.data4sci.com@bgoncalves Gradient Descent • Find the gradient for each training batch • Take a step downhill along the direction of the gradient 
 
 • where is the step size. • Repeat until “convergence”. H ✓mn ✓mn ↵ @H @✓mn @H @✓mn ↵
www.data4sci.com@bgoncalves
www.data4sci.com@bgoncalves Feed Forward Networks h t Output h t = f (xt) xt Input
www.data4sci.com@bgoncalves Feed Forward Networks h t xt Information
 Flow Input Output h t = f (xt)
www.data4sci.com@bgoncalves h t = f (xt, h t−1) Recurrent Neural Network (RNN) h t Output h t Output Previous Output Information
 Flow h t−1 h t = f (xt) xt Input
www.data4sci.com@bgoncalves Recurrent Neural Network (RNN) xt h t h t−1 h t xt+ 1 h t+ 1 h t+ 1 xt−1 h t−1 h t−2 • Each output depends (implicitly) on all previous outputs. • Input sequences generate output sequences (seq2seq)
www.data4sci.com@bgoncalves Recurrent Neural Network (RNN) h t h t h t−1 xt tanh h t = tanh (Wh t−1 + Uxt) Concatenate both inputs.
www.data4sci.com@bgoncalves Timeseries • Temporal sequence of data points • Consecutive points are strongly correlated • Common in statistics, signal processing, econometrics, mathematical finance, earthquake prediction, etc • Numeric (real or discrete) or symbolic data • Supervised Learning problem: Xt = f (Xt−1, ⋯, Xt−n )
github.com/DataForScience/RNN
www.data4sci.com@bgoncalves Long-Short Term Memory (LSTM) xt h t ct−1 ct xt+ 1 h t+ 1 ct+ 1 xt−1 h t−1 ct−2 • What if we want to keep explicit information about previous states (memory)? • How much information is kept, can be controlled through gates. h t−2 h t−1 h t h t+ 1 • LSTMs were first introduced in 1997 by Hochreiter and Schmidhuber
www.data4sci.com@bgoncalves σ σ f g × σ ×i o Long-Short Term Memory (LSTM) h t h t h t−1 xt ct−1 ct g = tanh (Wg h t−1 + Ug xt) ct = (ct−1 ⊗ f) + (g ⊗ i) h t = tanh (ct) ⊗ o +× × + 1− Element wise addition Element wise multiplication 1 minus the input tanh i = σ (Wih t−1 + Uixt) f = σ (Wf h t−1 + Uf xt) o = σ (Wo h t−1 + Uo xt) tanh
www.data4sci.com@bgoncalves σ σ f g × σ ×i o Long-Short Term Memory (LSTM) h t h t h t−1 xt ct−1 ct g = tanh (Wg h t−1 + Ug xt) ct = (ct−1 ⊗ f) + (g ⊗ i) h t = tanh (ct) ⊗ o +× × + 1− Element wise addition Element wise multiplication 1 minus the input tanh i = σ (Wih t−1 + Uixt) f = σ (Wf h t−1 + Uf xt) o = σ (Wo h t−1 + Uo xt) Forget gate:
 How much of the previous state should be kept? tanh
www.data4sci.com@bgoncalves σ σ f g × σ ×i o Long-Short Term Memory (LSTM) h t h t h t−1 xt ct−1 ct g = tanh (Wg h t−1 + Ug xt) ct = (ct−1 ⊗ f) + (g ⊗ i) h t = tanh (ct) ⊗ o +× × + 1− Element wise addition Element wise multiplication 1 minus the input tanh i = σ (Wih t−1 + Uixt) f = σ (Wf h t−1 + Uf xt) o = σ (Wo h t−1 + Uo xt) Input gate:
 How much of the previous output should be remembered? tanh
www.data4sci.com@bgoncalves σ σ f g × σ ×i o Long-Short Term Memory (LSTM) h t h t h t−1 xt ct−1 ct g = tanh (Wg h t−1 + Ug xt) ct = (ct−1 ⊗ f) + (g ⊗ i) h t = tanh (ct) ⊗ o +× × + 1− Element wise addition Element wise multiplication 1 minus the input tanh i = σ (Wih t−1 + Uixt) f = σ (Wf h t−1 + Uf xt) o = σ (Wo h t−1 + Uo xt) Output gate:
 How much of the previous output should contribute? All gates use the same inputs and activation functions, but different weights tanh
www.data4sci.com@bgoncalves σ σ f g × σ ×i o Long-Short Term Memory (LSTM) h t h t h t−1 xt ct−1 ct g = tanh (Wg h t−1 + Ug xt) ct = (ct−1 ⊗ f) + (g ⊗ i) h t = tanh (ct) ⊗ o +× × + 1− Element wise addition Element wise multiplication 1 minus the input tanh i = σ (Wih t−1 + Uixt) f = σ (Wf h t−1 + Uf xt) o = σ (Wo h t−1 + Uo xt) Output gate:
 How much of the previous output should contribute? tanh
www.data4sci.com@bgoncalves σ σ f g × σ ×i o Long-Short Term Memory (LSTM) h t h t h t−1 xt ct−1 ct g = tanh (Wg h t−1 + Ug xt) ct = (ct−1 ⊗ f) + (g ⊗ i) h t = tanh (ct) ⊗ o +× × + 1− Element wise addition Element wise multiplication 1 minus the input tanh i = σ (Wih t−1 + Uixt) f = σ (Wf h t−1 + Uf xt) o = σ (Wo h t−1 + Uo xt) State:
 Update the current state tanh
www.data4sci.com@bgoncalves σ σ f g × σ ×i o Long-Short Term Memory (LSTM) h t h t h t−1 xt ct−1 ct g = tanh (Wg h t−1 + Ug xt) ct = (ct−1 ⊗ f) + (g ⊗ i) h t = tanh (ct) ⊗ o +× × + 1− Element wise addition Element wise multiplication 1 minus the input tanh i = σ (Wih t−1 + Uixt) f = σ (Wf h t−1 + Uf xt) o = σ (Wo h t−1 + Uo xt) Output:
 Combine all available information. tanh
www.data4sci.com@bgoncalves Using LSTMs inputs W1 LSTM W2 Neuron inputs W1 LSTM inputs W1 LSTM inputs W1 LSTM inputs W1 LSTM inputs W1 LSTM inputs W1 LSTM inputs W1 LSTM Sequence Length #features #LSTMcells
github.com/DataForScience/RNN
www.data4sci.com@bgoncalves Applications • Language Modeling and Prediction • Speech Recognition • Machine Translation • Part-of-Speech Tagging • Sentiment Analysis • Summarization • Time series forecasting
www.data4sci.com@bgoncalves Neural Networks? h t h t h t−1 xt ct−1 ct
www.data4sci.com@bgoncalves Or legos? https://keras.io
www.data4sci.com@bgoncalves Keras • Open Source neural network library written in Python • TensorFlow, Microsoft Cognitive Toolkit or Theano backends • Enables fast experimentation • Created and maintained by François Chollet, a Google engineer. • Implements Layers, Objective/Loss functions, Activation functions, Optimizers, etc… https://keras.io
www.data4sci.com@bgoncalves Keras • keras.models.Sequential(layers=None, name=None)- is the workhorse. You use it to build a model layer by layer. Returns the object that we will use to build the model • keras.layers • Dense(units, activation=None, use_bias=True) - None means linear activation. Other options are, ’tanh’, ’sigmoid’, ’softmax’, ’relu’, etc. • Dropout(rate, seed=None) • Activation(activation) - Same as the activation option to Dense, can also be used to pass TensorFlow or Theano operations directly. • SimpleRNN(units, input_shape, activation='tanh', use_bias=True, dropout=0.0, return_sequences=False) • GRU(units, input_shape, activation='tanh', use_bias=True, dropout=0.0, return_sequences=False) https://keras.io
www.data4sci.com@bgoncalves Keras • model = Sequential() • model.add(layer) - Add a layer to the top of the model • model.compile(optimizer, loss) - We have to compile the model before we can use it • optimizer - ‘adam’, ‘sgd’, ‘rmsprop’, etc… • loss - ‘mean_squared_error’, ‘categorical_crossentropy’, ‘kullback_leibler_divergence’, etc… • model.fit(x=None, y=None, batch_size=None, epochs=1, verbose=1, validation_split=0.0, validation_data=None, shuffle=True) • model.predict(x, batch_size=32, verbose=0) - fit/predict interface https://keras.io
www.data4sci.com@bgoncalves Gated Recurrent Unit (GRU) • Introduced in 2014 by K. Cho • Meant to solve the Vanishing Gradient Problem • Can be considered as a simplification of LSTMs • Similar performance to LSTM in some applications, better performance for smaller datasets.
www.data4sci.com@bgoncalves σ tanh × σ × r cz Gated Recurrent Unit (GRU) h t h t h t−1 xt +× z = σ (Wzh t−1 + Uzxt) r = σ (Wrh t−1 + Urxt) c = tanh (Wc (h t−1 ⊗ r) + Ucxt) h t = (z ⊗ c) + ((1 − z) ⊗ h t−1) 1− × + 1− Element wise addition Element wise multiplication 1 minus the input
www.data4sci.com@bgoncalves σ tanh × σ × r cz Gated Recurrent Unit (GRU) h t h t h t−1 xt +× z = σ (Wzh t−1 + Uzxt) r = σ (Wrh t−1 + Urxt) c = tanh (Wc (h t−1 ⊗ r) + Ucxt) h t = (z ⊗ c) + ((1 − z) ⊗ h t−1) 1− × + 1− Element wise addition Element wise multiplication 1 minus the input Update gate:
 How much of the previous state should be kept?
www.data4sci.com@bgoncalves σ tanh × σ × r cz Gated Recurrent Unit (GRU) h t h t h t−1 xt +× z = σ (Wzh t−1 + Uzxt) r = σ (Wrh t−1 + Urxt) c = tanh (Wc (h t−1 ⊗ r) + Ucxt) h t = (z ⊗ c) + ((1 − z) ⊗ h t−1) 1− × + 1− Element wise addition Element wise multiplication 1 minus the input Reset gate:
 How much of the previous output should be removed?
www.data4sci.com@bgoncalves σ tanh × σ × r cz Gated Recurrent Unit (GRU) h t h t h t−1 xt +× z = σ (Wzh t−1 + Uzxt) r = σ (Wrh t−1 + Urxt) c = tanh (Wc (h t−1 ⊗ r) + Ucxt) h t = (z ⊗ c) + ((1 − z) ⊗ h t−1) 1− × + 1− Element wise addition Element wise multiplication 1 minus the input Current memory:
 What information do we remember right now?
www.data4sci.com@bgoncalves σ tanh × σ × r cz Gated Recurrent Unit (GRU) h t h t h t−1 xt +× z = σ (Wzh t−1 + Uzxt) r = σ (Wrh t−1 + Urxt) c = tanh (Wc (h t−1 ⊗ r) + Ucxt) h t = (z ⊗ c) + ((1 − z) ⊗ h t−1) 1− × + 1− Element wise addition Element wise multiplication 1 minus the input Output:
 Combine all available information.

More Related Content

PDF
Recommending for the World
byYves Raimond
 
PDF
Explainable AI
byDinesh V
 
PPTX
Machine Learning
byKumar P
 
PDF
LSTM
by佳蓉 倪
 
PPTX
Human Pose Estimation by Deep Learning
byWei Yang
 
PDF
An introduction to deep reinforcement learning
byBig Data Colombia
 
PPTX
Machine learning
byeonx_32
 
PDF
Recurrent Neural Networks
byRakuten Group, Inc.
 
Recommending for the World
byYves Raimond
 
Explainable AI
byDinesh V
 
Machine Learning
byKumar P
 
LSTM
by佳蓉 倪
 
Human Pose Estimation by Deep Learning
byWei Yang
 
An introduction to deep reinforcement learning
byBig Data Colombia
 
Machine learning
byeonx_32
 
Recurrent Neural Networks
byRakuten Group, Inc.
 

What's hot

PDF
Introduction to TCAV (ICML2018)
byThien Q. Tran
 
PDF
Markov decision process
byJie-Han Chen
 
PDF
Deep Reinforcement Learning and Its Applications
byBill Liu
 
PDF
Random number generator
bySyed Atif Naseem
 
PPTX
Artificial intelligence- Logic Agents
byNuruzzaman Milon
 
PPTX
Image classification using CNN
byNoura Hussein
 
DOCX
Sentiment analysis in twitter using python
byCloudTechnologies
 
PDF
Deeper Things: How Netflix Leverages Deep Learning in Recommendations and Se...
bySudeep Das, Ph.D.
 
PDF
Time, Context and Causality in Recommender Systems
byYves Raimond
 
PPTX
Recurrent Neural Network (RNN) | RNN LSTM Tutorial | Deep Learning Course | S...
bySimplilearn
 
PDF
Rishabh Mehrotra - Recommendations in a Marketplace: Personalizing Explainabl...
byMLconf
 
PPTX
Machine Learning Tutorial Part - 1 | Machine Learning Tutorial For Beginners ...
bySimplilearn
 
PDF
Deep Learning for Recommender Systems
byYves Raimond
 
PDF
GenAi LLMs Zero to Hero: Mastering GenAI
byShakeelAhmed286165
 
PDF
Real Time Systems
byDeepak John
 
PDF
Deep Learning for Computer Vision: Generative models and adversarial training...
byUniversitat Politècnica de Catalunya
 
PDF
Introduction of Deep Reinforcement Learning
byNAVER Engineering
 
PPT
CS583-supervised-learning.ppt CS583-supervised-learning
bycmpt cmpt
 
PPTX
Multilayer & Back propagation algorithm
byswapnac12
 
PDF
An introduction to reinforcement learning
byJie-Han Chen
 
Introduction to TCAV (ICML2018)
byThien Q. Tran
 
Markov decision process
byJie-Han Chen
 
Deep Reinforcement Learning and Its Applications
byBill Liu
 
Random number generator
bySyed Atif Naseem
 
Artificial intelligence- Logic Agents
byNuruzzaman Milon
 
Image classification using CNN
byNoura Hussein
 
Sentiment analysis in twitter using python
byCloudTechnologies
 
Deeper Things: How Netflix Leverages Deep Learning in Recommendations and Se...
bySudeep Das, Ph.D.
 
Time, Context and Causality in Recommender Systems
byYves Raimond
 
Recurrent Neural Network (RNN) | RNN LSTM Tutorial | Deep Learning Course | S...
bySimplilearn
 
Rishabh Mehrotra - Recommendations in a Marketplace: Personalizing Explainabl...
byMLconf
 
Machine Learning Tutorial Part - 1 | Machine Learning Tutorial For Beginners ...
bySimplilearn
 
Deep Learning for Recommender Systems
byYves Raimond
 
GenAi LLMs Zero to Hero: Mastering GenAI
byShakeelAhmed286165
 
Real Time Systems
byDeepak John
 
Deep Learning for Computer Vision: Generative models and adversarial training...
byUniversitat Politècnica de Catalunya
 
Introduction of Deep Reinforcement Learning
byNAVER Engineering
 
CS583-supervised-learning.ppt CS583-supervised-learning
bycmpt cmpt
 
Multilayer & Back propagation algorithm
byswapnac12
 
An introduction to reinforcement learning
byJie-Han Chen
 

Similar to RNNs for Timeseries Analysis

PDF
Recurrent Neural Networks
bySharath TS
 
PDF
Recurrent Neural Networks. Part 1: Theory
byAndrii Gakhov
 
PPT
14889574 dl ml RNN Deeplearning MMMm.ppt
byManiMaran230751
 
PPTX
RNN-LSTM.pptx
byssuserc755f1
 
PDF
Rnn presentation 2
byShubhangi Tandon
 
PDF
rnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
bykhushbu maurya
 
PPTX
Understanding Deep Learning Recurrent Neural Networks.pptx
byjainamulyawin
 
PDF
Recurrent Neural Networks (RNN) | RNN LSTM | Deep Learning Tutorial | Tensorf...
byEdureka!
 
PPTX
recurrent nural networks in best teaching way
byswethasetty5
 
PDF
Recurrent neural networks rnn
byKuppusamy P
 
PDF
Learning Financial Market Data with Recurrent Autoencoders and TensorFlow
byAltoros
 
PPTX
Recurrent Neural Networks (RNNs)
byAbdullah al Mamun
 
PPTX
RNN and LSTM model description and working advantages and disadvantages
byAbhijitVenkatesh1
 
PPTX
RNN-LSTM.pptx
byssuserc755f1
 
PDF
Backpropagation in RNN and LSTM
byHimanshuSingh1370
 
PPTX
Introduction to deep learning
byJunaid Bhat
 
PDF
Hardware Acceleration for Machine Learning
byCastLabKAIST
 
PDF
Machine Learning for Trading
byLarry Guo
 
PPTX
Dataworkz odsc london 2018
byOlaf de Leeuw
 
PDF
Recurrent Neural Networks, LSTM and GRU
byananth
 
Recurrent Neural Networks
bySharath TS
 
Recurrent Neural Networks. Part 1: Theory
byAndrii Gakhov
 
14889574 dl ml RNN Deeplearning MMMm.ppt
byManiMaran230751
 
RNN-LSTM.pptx
byssuserc755f1
 
Rnn presentation 2
byShubhangi Tandon
 
rnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
bykhushbu maurya
 
Understanding Deep Learning Recurrent Neural Networks.pptx
byjainamulyawin
 
Recurrent Neural Networks (RNN) | RNN LSTM | Deep Learning Tutorial | Tensorf...
byEdureka!
 
recurrent nural networks in best teaching way
byswethasetty5
 
Recurrent neural networks rnn
byKuppusamy P
 
Learning Financial Market Data with Recurrent Autoencoders and TensorFlow
byAltoros
 
Recurrent Neural Networks (RNNs)
byAbdullah al Mamun
 
RNN and LSTM model description and working advantages and disadvantages
byAbhijitVenkatesh1
 
RNN-LSTM.pptx
byssuserc755f1
 
Backpropagation in RNN and LSTM
byHimanshuSingh1370
 
Introduction to deep learning
byJunaid Bhat
 
Hardware Acceleration for Machine Learning
byCastLabKAIST
 
Machine Learning for Trading
byLarry Guo
 
Dataworkz odsc london 2018
byOlaf de Leeuw
 
Recurrent Neural Networks, LSTM and GRU
byananth
 

More from Bruno Gonçalves

PDF
Blockchain Technologies for Data Science
byBruno Gonçalves
 
PDF
Data Visualization using matplotlib
byBruno Gonçalves
 
PDF
Spatio Temporal Analysis of Language use.
byBruno Gonçalves
 
PDF
Word2vec and Friends
byBruno Gonçalves
 
PDF
Word2vec in Theory Practice with TensorFlow
byBruno Gonçalves
 
PDF
Word2vec and Friends
byBruno Gonçalves
 
PDF
Machine(s) Learning with Neural Networks
byBruno Gonçalves
 
PDF
A practical Introduction to Machine(s) Learning
byBruno Gonçalves
 
PDF
Making Sense of Data Big and Small
byBruno Gonçalves
 
PDF
Human Mobility (with Mobile Devices)
byBruno Gonçalves
 
PDF
Twitterology - The Science of Twitter
byBruno Gonçalves
 
PDF
Mining Georeferenced Data
byBruno Gonçalves
 
Blockchain Technologies for Data Science
byBruno Gonçalves
 
Data Visualization using matplotlib
byBruno Gonçalves
 
Spatio Temporal Analysis of Language use.
byBruno Gonçalves
 
Word2vec and Friends
byBruno Gonçalves
 
Word2vec in Theory Practice with TensorFlow
byBruno Gonçalves
 
Word2vec and Friends
byBruno Gonçalves
 
Machine(s) Learning with Neural Networks
byBruno Gonçalves
 
A practical Introduction to Machine(s) Learning
byBruno Gonçalves
 
Making Sense of Data Big and Small
byBruno Gonçalves
 
Human Mobility (with Mobile Devices)
byBruno Gonçalves
 
Twitterology - The Science of Twitter
byBruno Gonçalves
 
Mining Georeferenced Data
byBruno Gonçalves
 

Recently uploaded

PDF
Whitepaper / No code end-user app development (2026)
byOptymyze
 
PPTX
Toxicity symptoms in plants due to higher concentration
byranveer02yadav
 
PDF
Unlock Data Diode Cyber Threat Analytics, Predict Attacks Before They Happen_...
byWynyard Group
 
PPTX
Microsoft-Dynamics-365-Business-Central (1).pptx
byUlirRohwana
 
PPTX
7.__Developing_a_Research_Proposal[1].pptx
bynahomeshetu340
 
PPTX
Internship ppt about multiple disease prediction
byGOUTHAMTr2
 
PPTX
Query Parsing: The SEO Gatekeeper That Decides Rankings
bySemantic SEO BD
 
PDF
Content Strategy Presentation.pdfjjjjhhhhh
byCerineAmmarkhodja1
 
PDF
CodeMate_Autonomous_Engineering_Documents.pdf
byssuserc287c9
 
PDF
What is Context Engineering for Agentforce Developer and Architect
byParis Salesforce Developer Group
 
PPTX
maaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
byAshleyJane9
 
PDF
"Top Excel Tips and Tricks: Conditional Formatting, Sorting, and More - Learn...
byCA Suvidha Chaplot
 
PPTX
Quartiles_Ungrouped_Data_Grade_10-1.pptx
byxiandexter21
 
PDF
제 23회 보아즈(BOAZ) 빅데이터 컨퍼런스 - [MBOAX] : ABSA를 활용한 소비자 반응 분석 기반 운영 효율화 대시보드 설계
byBOAZ Bigdata
 
PDF
Social Media in Gurgaon: Strategies, Services & Solutions by Bala Infotech
byBala Infotech
 
PPTX
Hacking-Uncovered-How-People-Get-Hacked-and-How-to-Stay-Safe[1].pptx
bylegendgaminghari
 
PPTX
TreatmentPlan of gingival diseases and options
byMohamadSaid29
 
PDF
TOS in History.pdf ENGLISH macro.pdf mnbv
bykristinegorre7
 
PDF
Top 10 Excel Tips for Efficiency | Learn Advanced Excel Techniques CA SUVIDHA...
byCA Suvidha Chaplot
 
PDF
"Essential Excel Tips for Beginners & Professionals – 50+ Techniques to Maste...
byCA Suvidha Chaplot
 
Whitepaper / No code end-user app development (2026)
byOptymyze
 
Toxicity symptoms in plants due to higher concentration
byranveer02yadav
 
Unlock Data Diode Cyber Threat Analytics, Predict Attacks Before They Happen_...
byWynyard Group
 
Microsoft-Dynamics-365-Business-Central (1).pptx
byUlirRohwana
 
7.__Developing_a_Research_Proposal[1].pptx
bynahomeshetu340
 
Internship ppt about multiple disease prediction
byGOUTHAMTr2
 
Query Parsing: The SEO Gatekeeper That Decides Rankings
bySemantic SEO BD
 
Content Strategy Presentation.pdfjjjjhhhhh
byCerineAmmarkhodja1
 
CodeMate_Autonomous_Engineering_Documents.pdf
byssuserc287c9
 
What is Context Engineering for Agentforce Developer and Architect
byParis Salesforce Developer Group
 
maaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
byAshleyJane9
 
"Top Excel Tips and Tricks: Conditional Formatting, Sorting, and More - Learn...
byCA Suvidha Chaplot
 
Quartiles_Ungrouped_Data_Grade_10-1.pptx
byxiandexter21
 
제 23회 보아즈(BOAZ) 빅데이터 컨퍼런스 - [MBOAX] : ABSA를 활용한 소비자 반응 분석 기반 운영 효율화 대시보드 설계
byBOAZ Bigdata
 
Social Media in Gurgaon: Strategies, Services & Solutions by Bala Infotech
byBala Infotech
 
Hacking-Uncovered-How-People-Get-Hacked-and-How-to-Stay-Safe[1].pptx
bylegendgaminghari
 
TreatmentPlan of gingival diseases and options
byMohamadSaid29
 
TOS in History.pdf ENGLISH macro.pdf mnbv
bykristinegorre7
 
Top 10 Excel Tips for Efficiency | Learn Advanced Excel Techniques CA SUVIDHA...
byCA Suvidha Chaplot
 
"Essential Excel Tips for Beginners & Professionals – 50+ Techniques to Maste...
byCA Suvidha Chaplot
 

RNNs for Timeseries Analysis