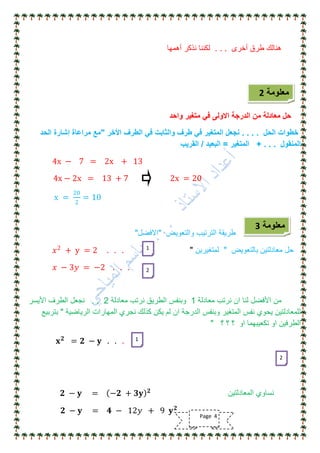
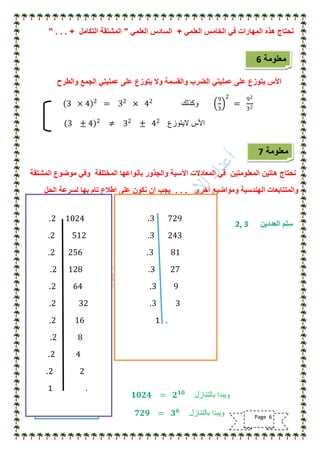
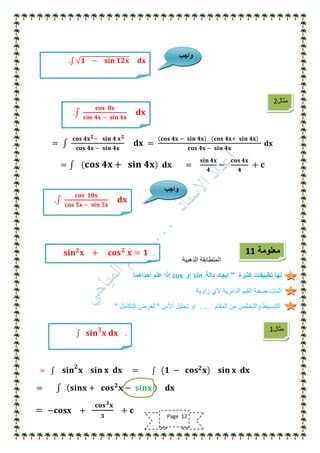
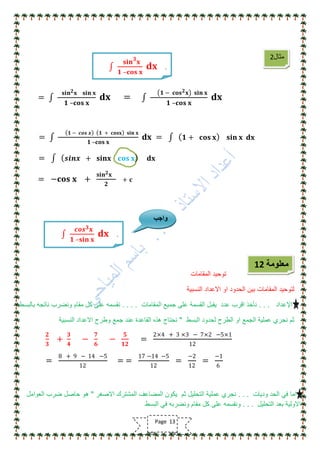
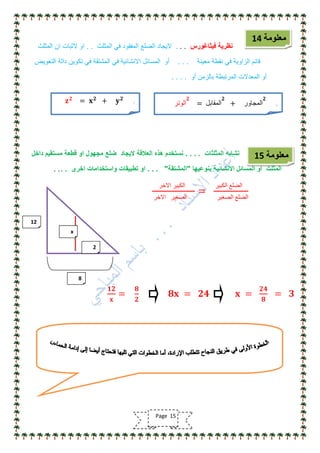
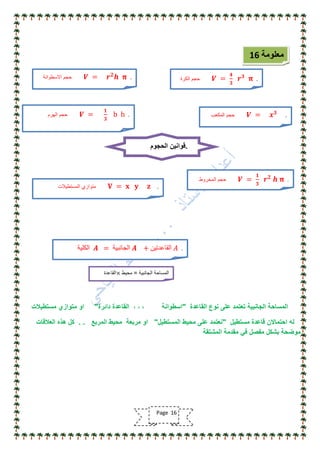
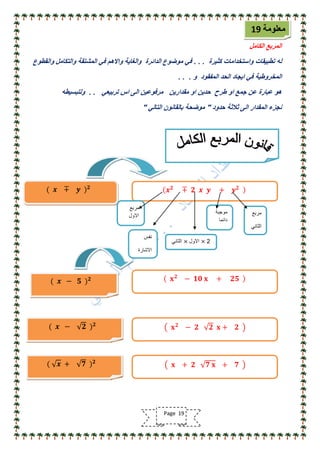
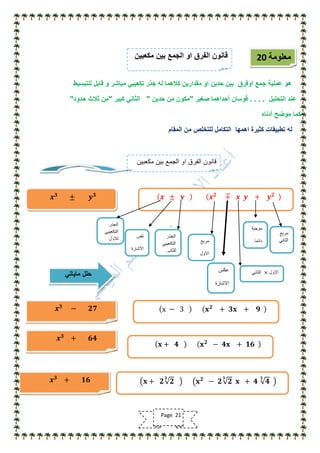
تناقش الوثيقة أهمية مادة الرياضيات وتوجيه الدراسة لتحقيق النجاح الأكاديمي، مشددة على ضرورة التركيز على الأساسيات ومهارات الحل. كما تقدم نصائح للطلاب حول كيفية التعامل مع المناهج الدراسية وتحديد أوقات المراجعة الفعالة. وتؤكد الوثيقة على الاستمرار في تطوير الطرق التعليمية والتكيف مع الأساليب المختلفة لتحسين الأداء في الرياضيات.