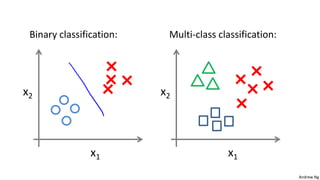
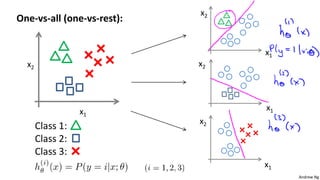
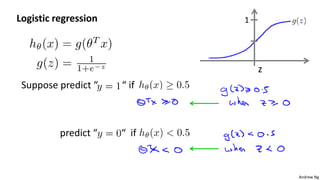
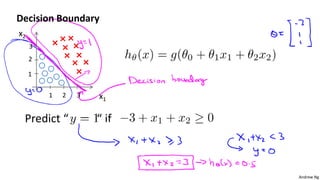
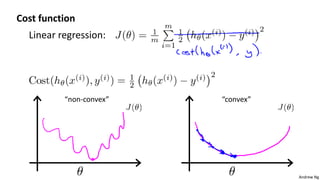
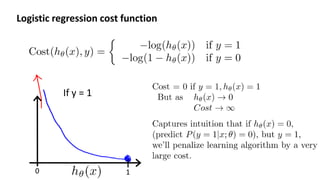
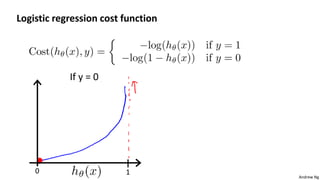
This document discusses logistic regression for classification problems. Logistic regression models the probability of an output belonging to a particular class using a logistic function. The model parameters are estimated by minimizing a cost function using gradient descent or other advanced optimization algorithms. Logistic regression can be extended to multi-class classification problems using a one-vs-all approach that trains a separate binary classifier for each class.

1. Logistic
Regression
Classification
Machine Learning

2. Andrew Ng
Classification
Email: Spam / Not Spam?
Online Transactions: Fraudulent (Yes / No)?
Tumor: Malignant / Benign ?
0: “Negative Class” (e.g., benign tumor)
1: “Positive Class” (e.g., malignant tumor)

3. Andrew Ng
Tumor Size
Threshold classifier output at 0.5:
If , predict “y = 1”
If , predict “y = 0”
Tumor Size
Malignant ?
(Yes) 1
(No) 0
0.5

4. Andrew Ng
Classification: y = 0 or 1
can be > 1 or < 0
Logistic Regression:

5. Logistic
Regression
Hypothesis
Representation
Machine Learning

6. Andrew Ng
Sigmoid function
Logistic function
Logistic Regression Model
Want
0
1
0.5

7. Andrew Ng
Interpretation of Hypothesis Output
= estimated probability that y = 1 for input x
Tell patient that 70% chance of tumor being malignant
Example: If
“probability that y = 1, given x,
parameterized by ”

8. Logistic
Regression
Decision boundary
Machine Learning

9. Andrew Ng
Logistic regression
Suppose predict “ “ if
predict “ “ if
z
1

10. Andrew Ng
x1
x2
Decision Boundary
1 2 3
1
2
3
Predict “ “ if

11. Andrew Ng
Non-linear decision boundaries
x1
x2
Predict “ “ if
x1
x2
1-1
-1
1

12. Logistic
Regression
Cost function
Machine Learning

13. Andrew Ng
Training set:
How to choose parameters ?
m examples

14. Andrew Ng
Cost function
Linear regression:
“non-convex” “convex”

15. Andrew Ng
Logistic regression cost function
If y = 1
10

16. Andrew Ng
Logistic regression cost function
If y = 0
10

17. Logistic
Regression
Simplified cost function
and gradient descent
Machine Learning

18. Andrew Ng
Logistic regression cost function

19. Andrew Ng
Output
Logistic regression cost function
To fit parameters :
To make a prediction given new :

20. Andrew Ng
Gradient Descent
Want :
Repeat
(simultaneously update all )

21. Andrew Ng
Gradient Descent
Want :
(simultaneously update all )
Repeat
Algorithm looks identical to linear regression!

22. Logistic
Regression
Advanced
optimization
Machine Learning

23. Andrew Ng
Optimization algorithm
Cost function . Want .
Given , we have code that can compute
-
- (for )
Repeat
Gradient descent:

24. Andrew Ng
Optimization algorithm
Given , we have code that can compute
-
- (for )
Optimization algorithms:
- Gradient descent
- Conjugate gradient
- BFGS
- L-BFGS
Advantages:
- No need to manually pick
- Often faster than gradient
descent.
Disadvantages:
- More complex

25. Andrew Ng
Example:
function [jVal, gradient]
= costFunction(theta)
jVal = (theta(1)-5)^2 + ...
(theta(2)-5)^2;
gradient = zeros(2,1);
gradient(1) = 2*(theta(1)-5);
gradient(2) = 2*(theta(2)-5);
options = optimset(‘GradObj’, ‘on’, ‘MaxIter’, ‘100’);
initialTheta = zeros(2,1);
[optTheta, functionVal, exitFlag] ...
= fminunc(@costFunction, initialTheta, options);

26. Andrew Ng
gradient(1) = [ ];
function [jVal, gradient] = costFunction(theta)
theta =
jVal = [ ];
gradient(2) = [ ];
gradient(n+1) = [ ];
code to compute
code to compute
code to compute
code to compute

27. Logistic
Regression
Multi-class classification:
One-vs-all
Machine Learning

28. Andrew Ng
Multiclass classification
Email foldering/tagging: Work, Friends, Family, Hobby
Medical diagrams: Not ill, Cold, Flu
Weather: Sunny, Cloudy, Rain, Snow

29. Andrew Ng
x1
x2
x1
x2
Binary classification: Multi-class classification:

30. Andrew Ng
x1
x2
One-vs-all (one-vs-rest):
Class 1:
Class 2:
Class 3:
x1
x2
x1
x2
x1
x2

31. Andrew Ng
One-vs-all
Train a logistic regression classifier for each
class to predict the probability that .
On a new input , to make a prediction, pick the
class that maximizes