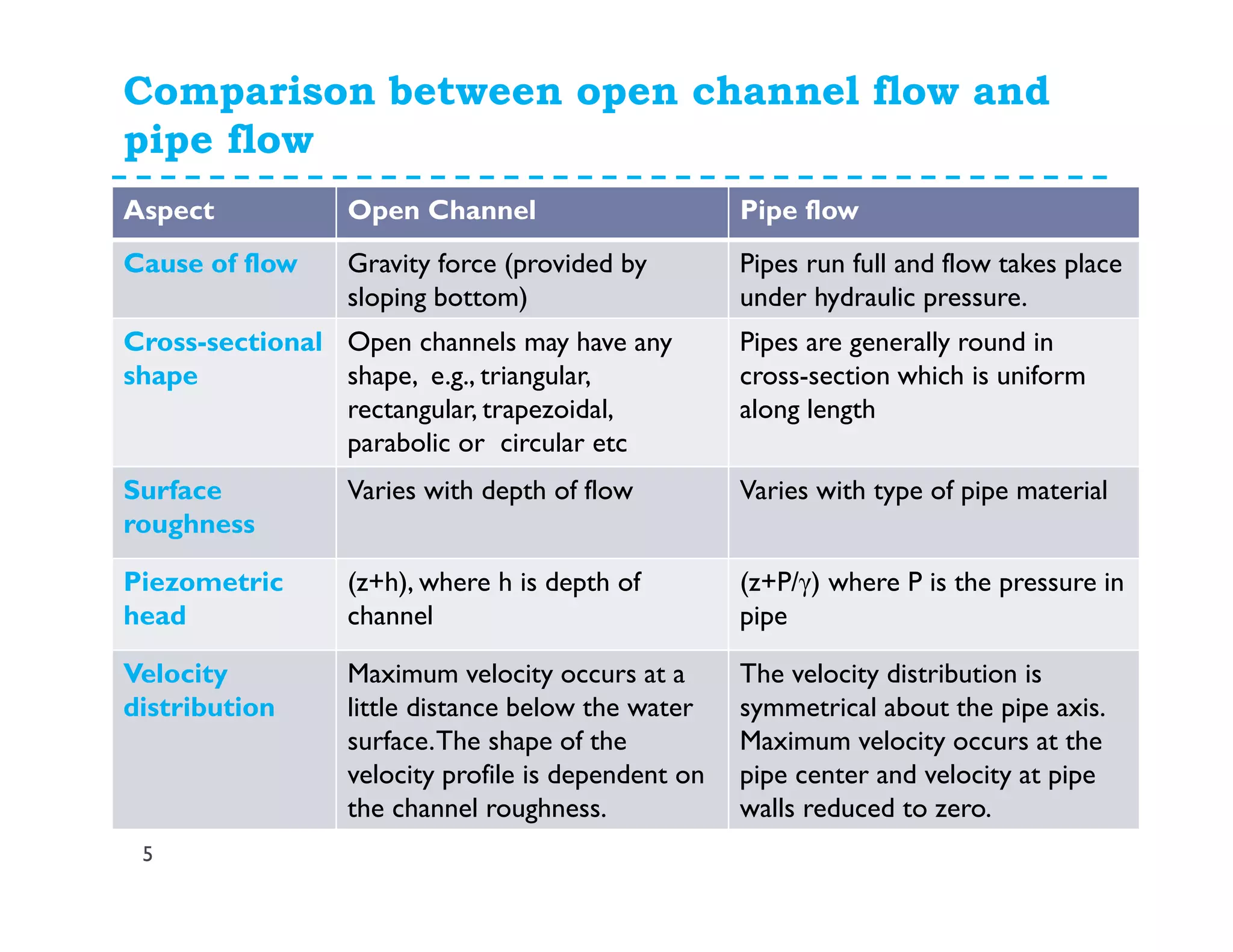
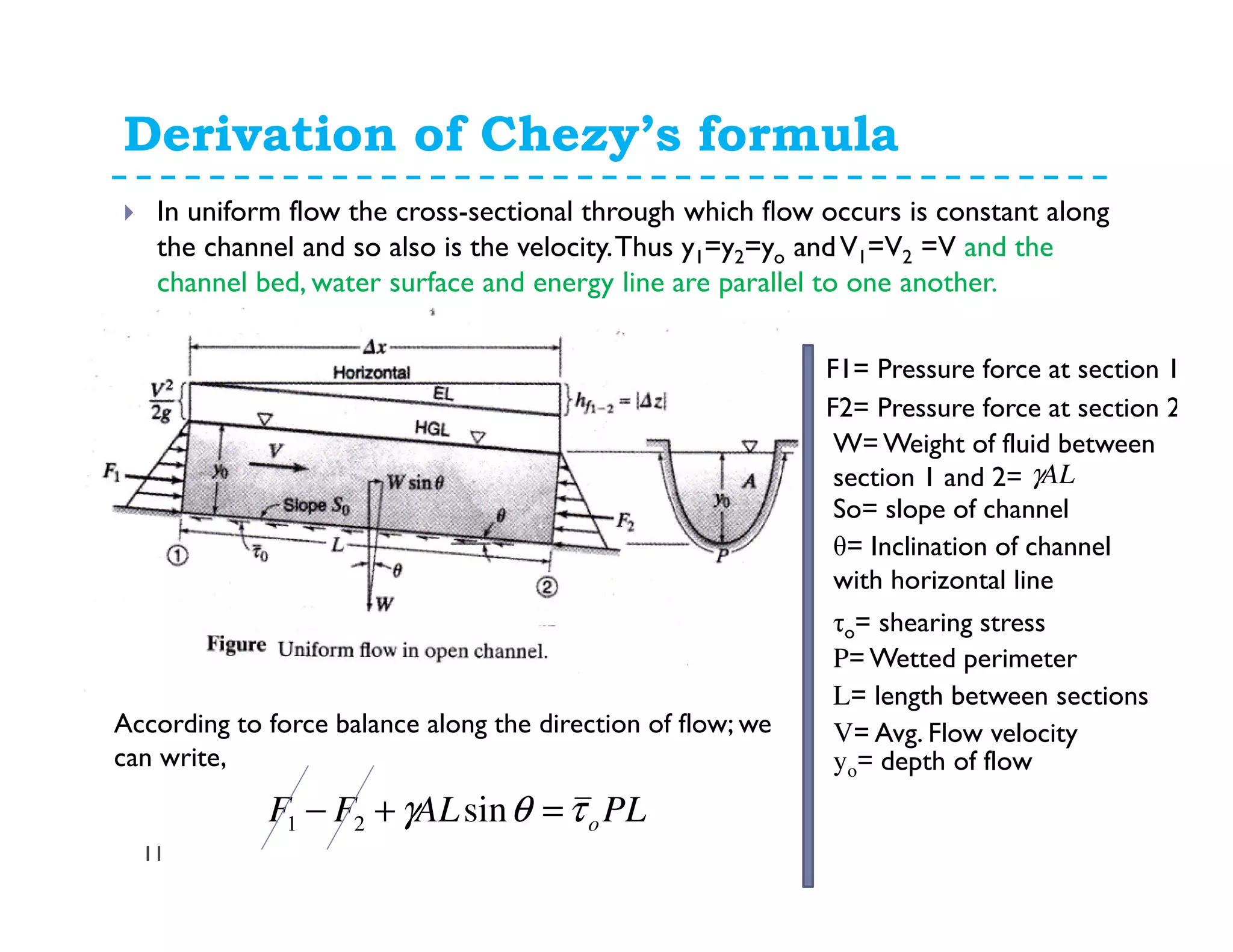
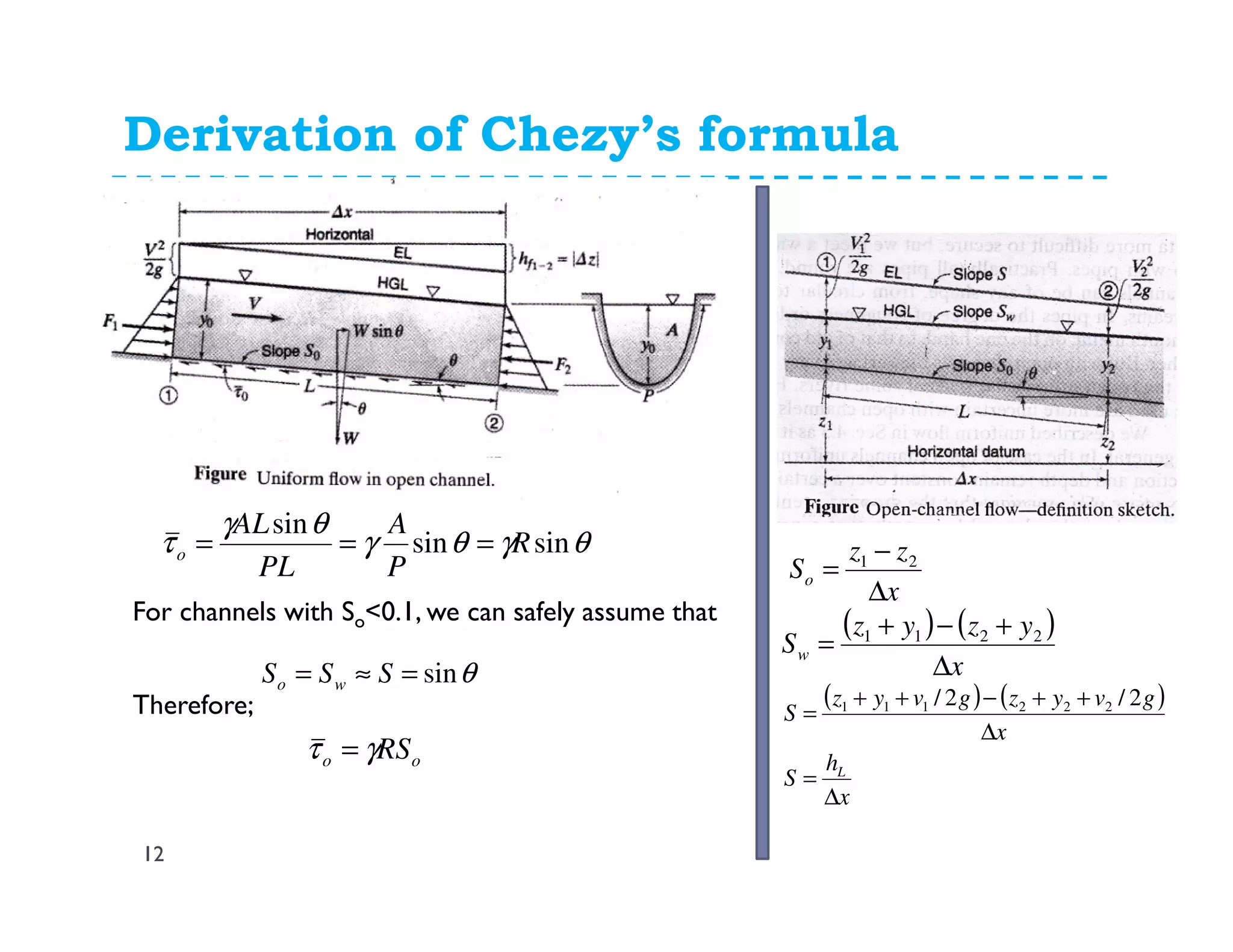
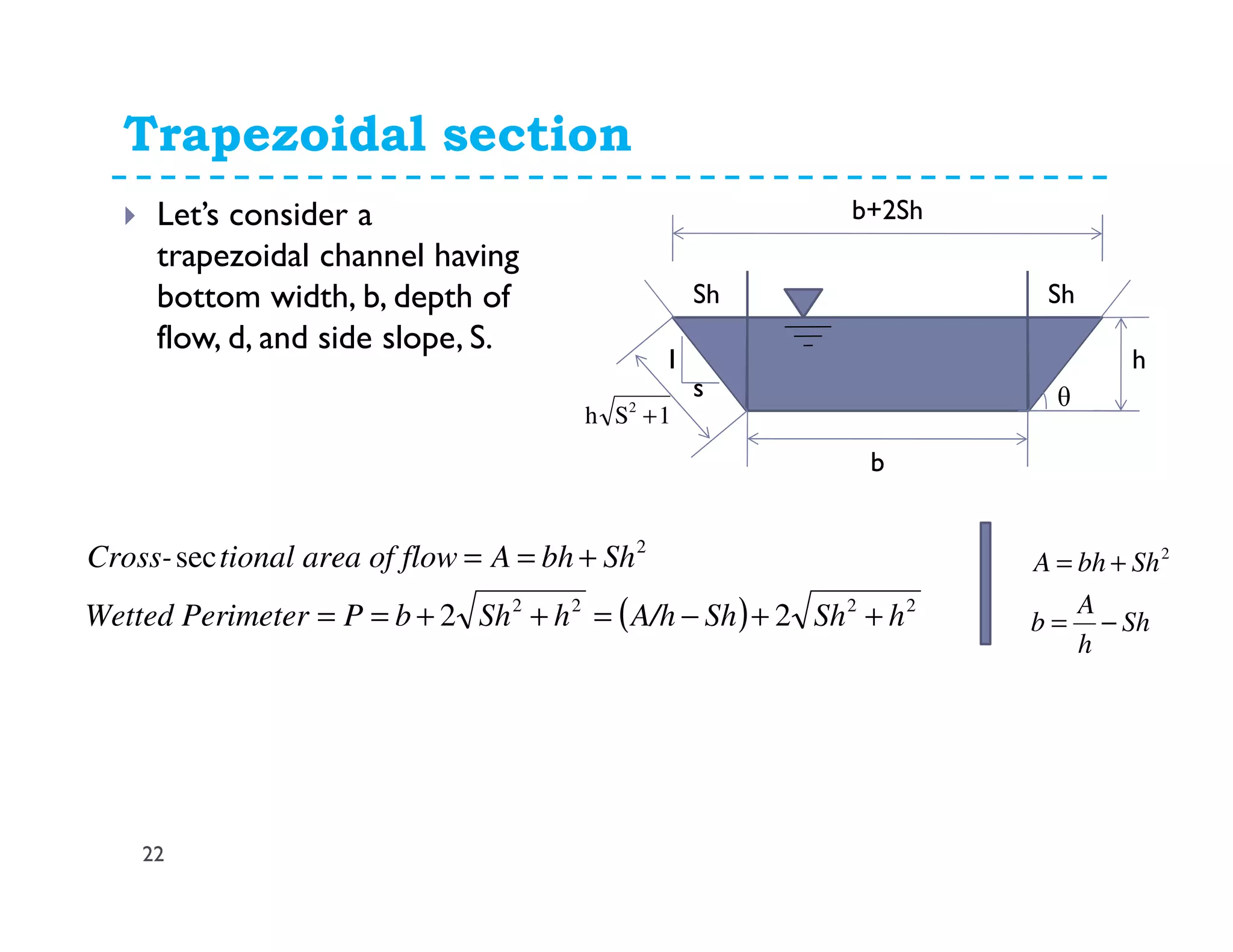
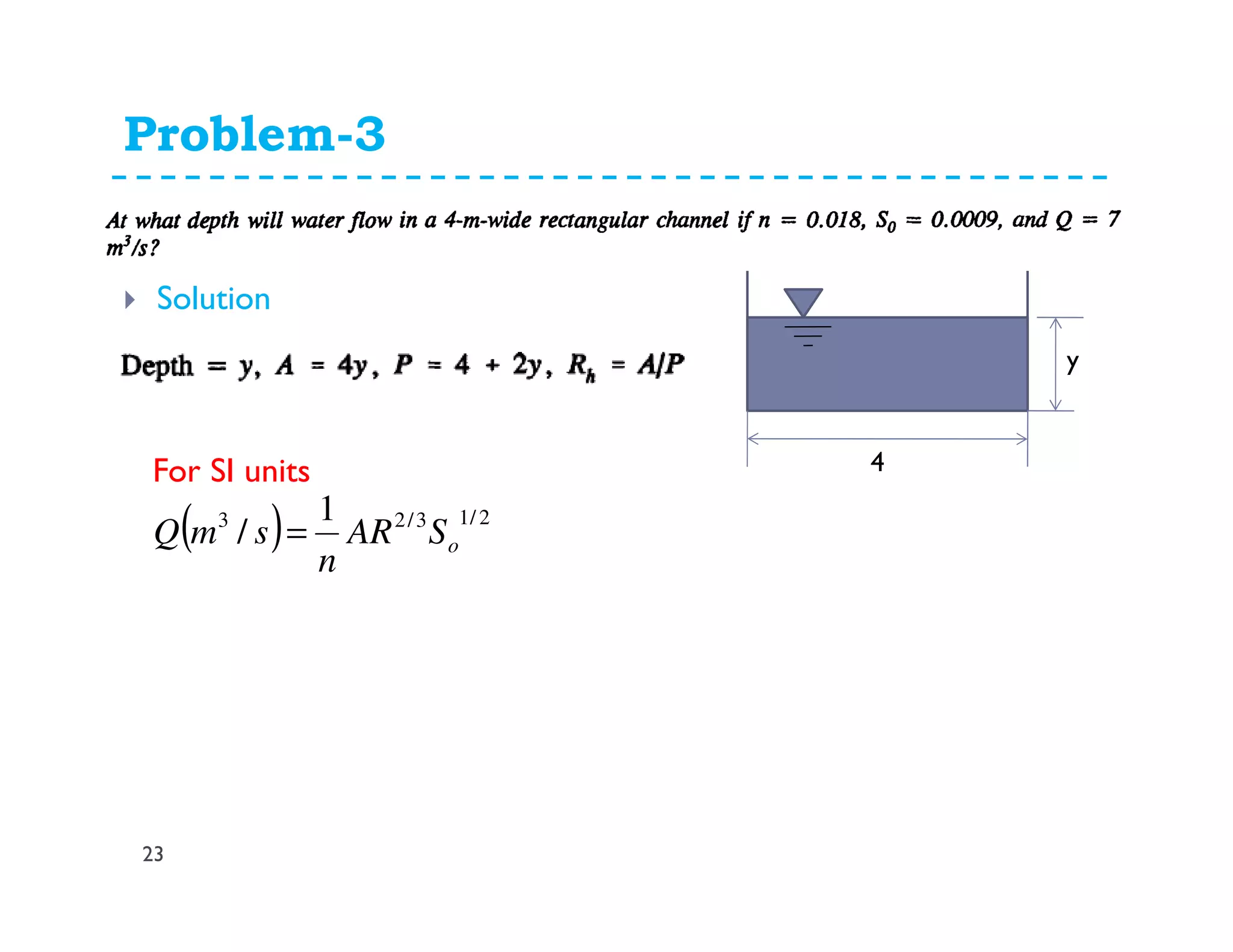
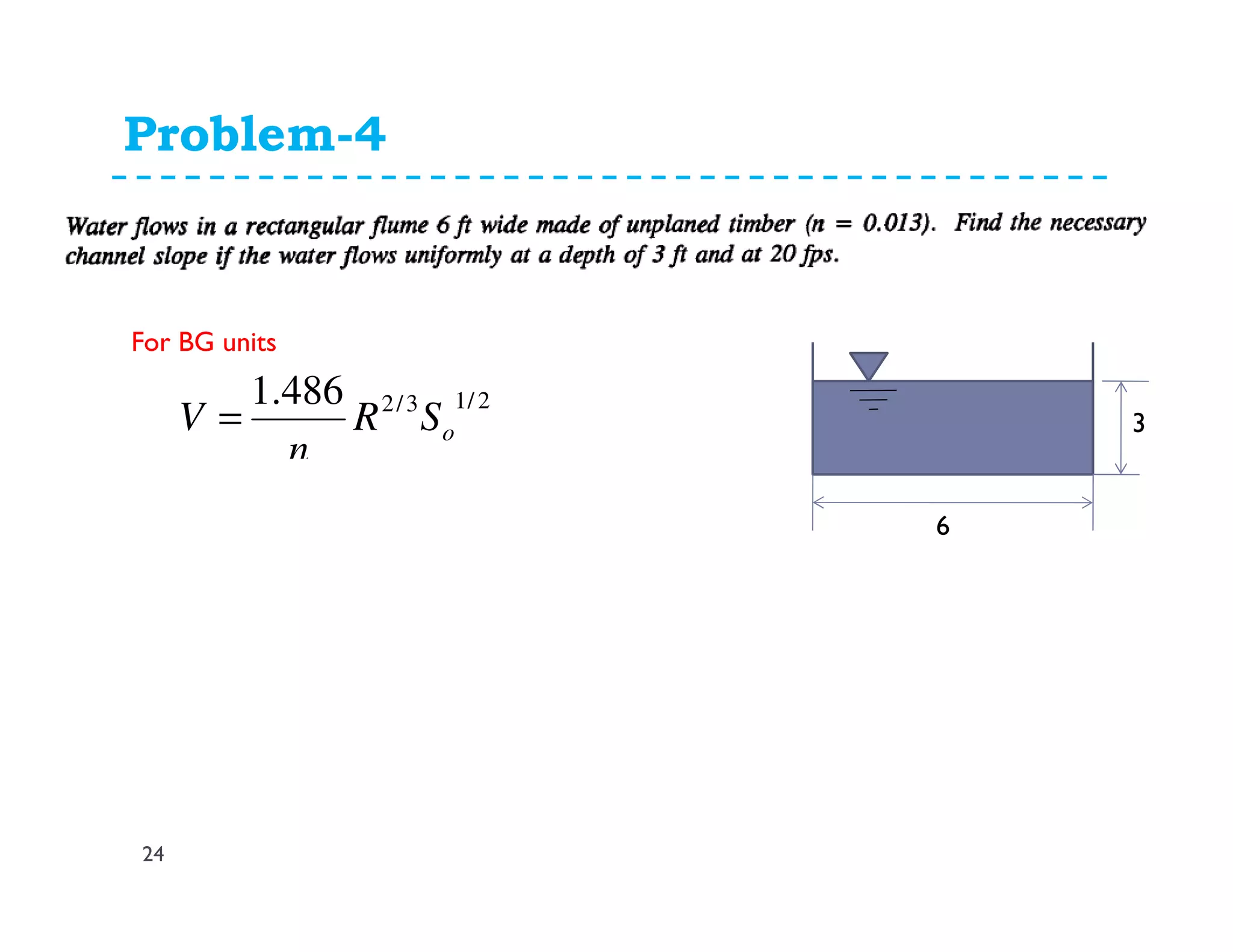
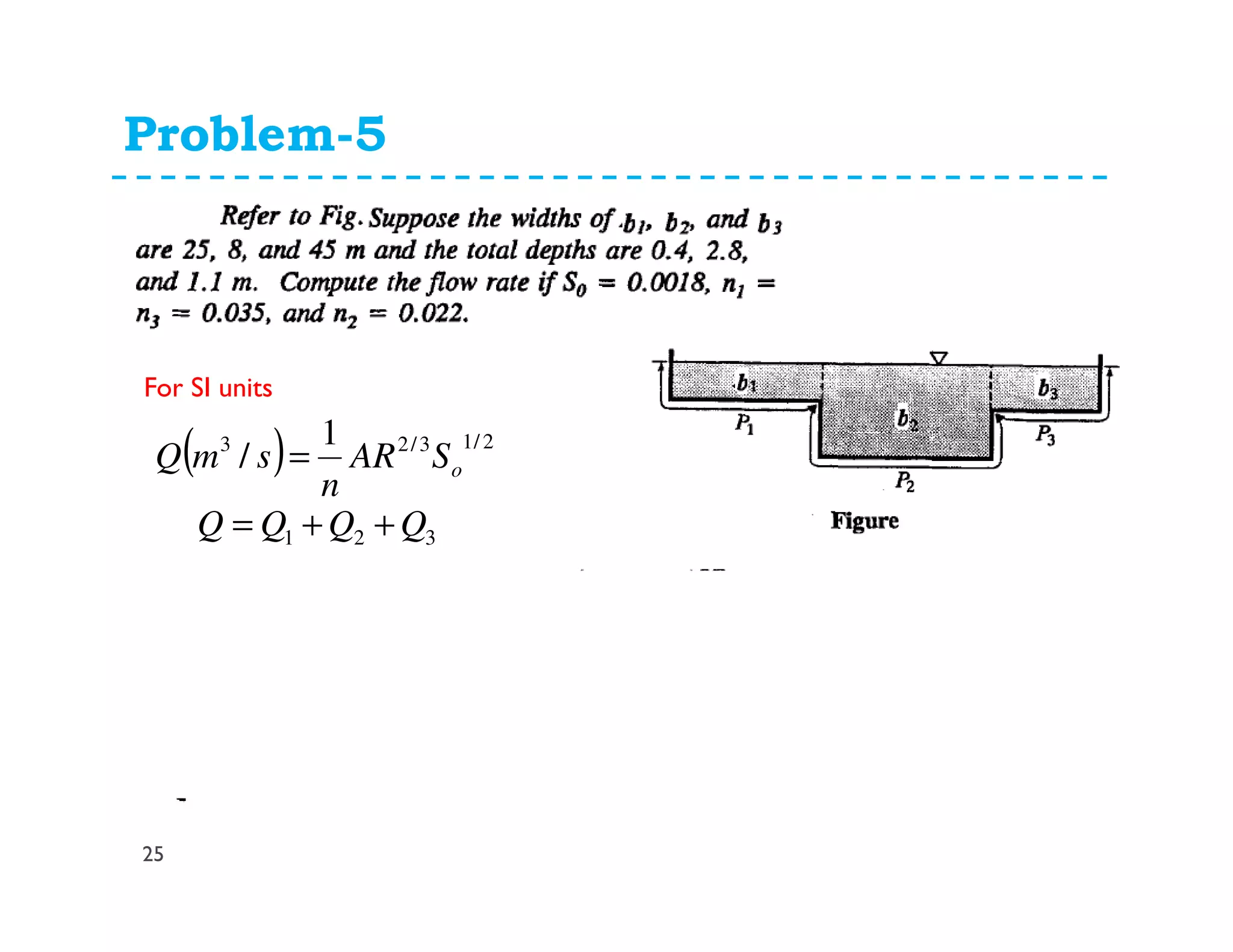
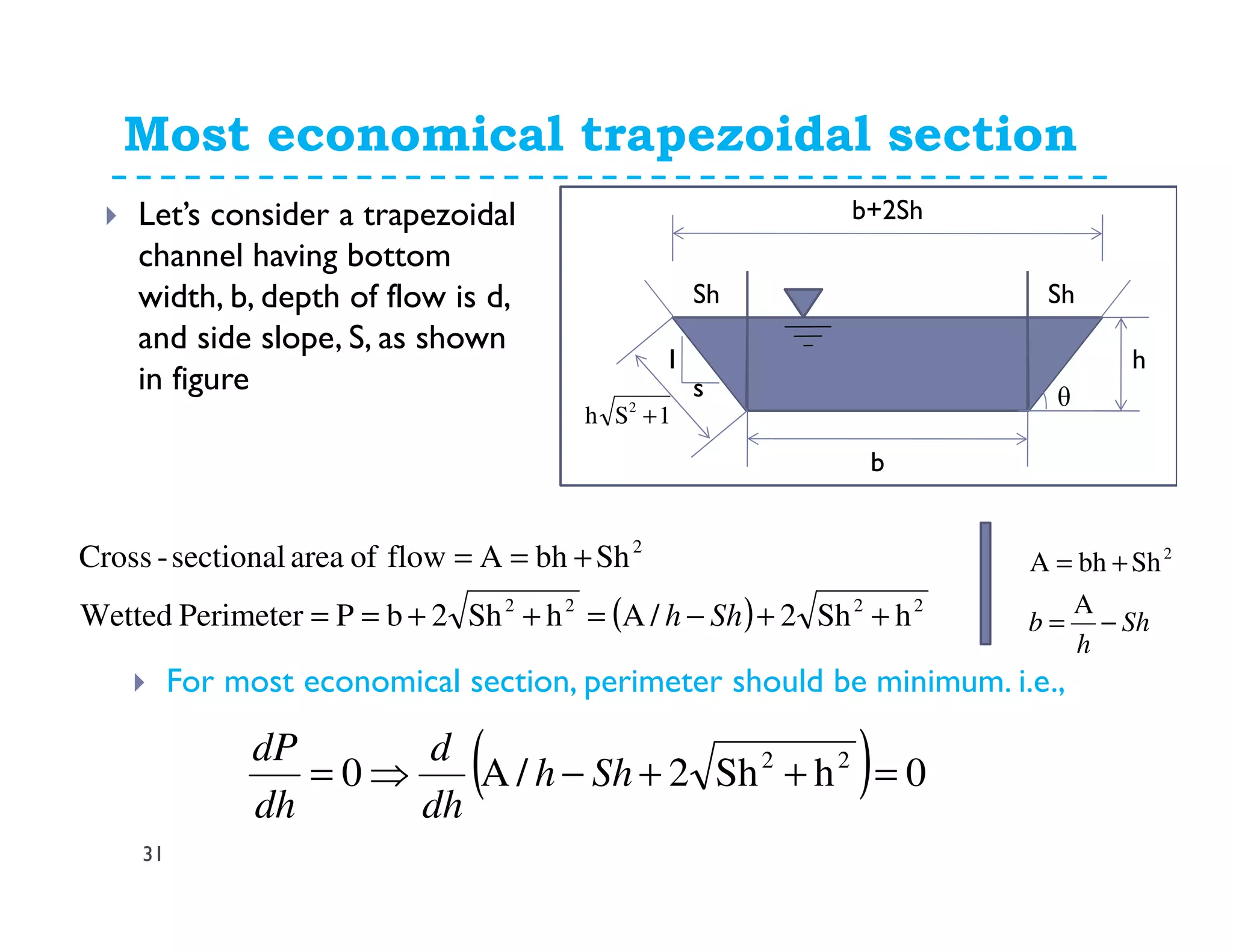
The document discusses open channel flow, providing definitions and key equations. It begins by defining an open channel as a channel with a free surface not fully enclosed by solid boundaries. Important equations for open channel flow are then presented, including Chezy's and Manning's equations for calculating velocity and discharge using variables like hydraulic radius, channel slope, and roughness coefficients. Factors influencing open channel flow like channel shape, surface roughness, and flow regime (e.g. laminar vs turbulent) are also addressed.

1. Dynamics of Fluid Flow in Open Channel
Flow: Concept of open channel, Chezy’s and
Manning’s equations for open channel and their
application.
1
Fluid Mechanics
Dr. Mohsin Siddique
Assistant Professor

2. Outcome of Today’s Lecture
2
After completing this lecture…
The students should be able to:
Understand the concepts and basic equations used in open
channel flow
Determine the velocity and discharge using Chezy’s and
Manning’s equation
Understand the concept of most economical sections

3. Open Channel Flow
3
An open channel is the one in which stream is not
complete enclosed by solid boundaries and therefore has a
free surface subjected only to atmosphere pressure.
The flow in such channels is not caused by some external
head, but rather only by gravitational component along the
slope of channel. Thus open channel flow is also referred to as
free surface flow or gravity flow.
Examples of open channel are
Rivers, canals, streams, & sewerage system etc

4. Open Channel Flow
4
Thal Canal Indus river

5. Comparison between open channel flow and
pipe flow
5
Aspect Open Channel Pipe flow
Cause of flow Gravity force (provided by
sloping bottom)
Pipes run full and flow takes place
under hydraulic pressure.
Cross-sectional
shape
Open channels may have any
shape, e.g., triangular,
rectangular, trapezoidal,
parabolic or circular etc
Pipes are generally round in
cross-section which is uniform
along length
Surface
roughness
Varies with depth of flow Varies with type of pipe material
Piezometric
head
(z+h), where h is depth of
channel
(z+P/γ) where P is the pressure in
pipe
Velocity
distribution
Maximum velocity occurs at a
little distance below the water
surface.The shape of the
velocity profile is dependent on
the channel roughness.
The velocity distribution is
symmetrical about the pipe axis.
Maximum velocity occurs at the
pipe center and velocity at pipe
walls reduced to zero.

6. Types of Channels
6
Natural Channels: It is one with irregular sections of varying shapes,
developing in natural way. .e.g., rivers, streams etc
Artificial Channels: It is the one built artificially for carrying water for
various purposes. e.g., canals,
Open Channel: A channel without any cover at the top. e.g., canals, rivers
streams etc
Covered Channels: A channel having cover at the top. e.g., partially filled
conduits carrying water
Prismatic Channels:A channel with constant bed slope and cross-section
along its length.

7. Types of flow in open channels
7
Steady and unsteady flow
Uniform and non-uniform flow
Laminar andTurbulent flow
Subcritical, critical and supercritical flow
Same definition
with pipe flows
Laminar and Turbulent flow: For open channels, it is defined with
Reynolds No. as;
ν
h
e
VR
R =
νν
h
e
VRVD
R
4
==
Remember in pipe flows
Therefore,
For laminar flow: Re <= 500
For transitional flow: 500 <Re< 1000
ForTurbulent flow: Re >= 1000
For laminar flow: Re <= 2000

8. Types of flow in open channels
8
Subcritical, Critical and Supercritical Flow.These are classified with
Froude number.
Froude No. (Fr). It is ratio of inertial force to gravitational force of
flowing fluid. Mathematically, Froude no. is
If
Fr. < 1, Flow is subcritical flow
Fr. = 1, Flow is critical flow
Fr. > 1, Flow is supercritical flow
gh
V
Fr =
Where, V is average velocity of flow, h is depth of flow and g is gravitational
acceleration

9. Definitions
9
Depth of Flow: It is the vertical distance of the lowest point of a
channel section(bed of the channel) from the free surface.
Depth of Flow Section: It is depth of flow normal to bed of the
channel.
Top Width: It is the width of channel section at the free surface.
Wetted Area: It is the cross-sectional area of the flow section of
channel.
Wetted Perimeter: It is the length of channel boundary in
contact with the flowing water at any section.
Hydraulic Radius: It is ratio of cross-sectional area of flow to
wetted perimeter.

10. Open channel formulae for uniform flow
10
For uniform flow in open channels, following formulae are widely used
oRSCV =
2/13/21
oSR
n
V =
Here,
V=Average flow velocity
R=Hydraulic radius
So=Channel bed slope
C= Chezy’s constant
n= Manning’s Roughness coefficient
1. Chezy’s Formula: Antoine de Chezy (1718-1798), a
French bridge and hydraulic expert, proposed his
formula in 1775.
2. Manning’s Formula: Rober Manning (An Irish
engineer) proposed the following relation for
Chezy’s coefficient C
( ) 6/1
/1 RnC =
According to which Chezy’s equation can be written as

11. Derivation of Chezy’s formula
11
In uniform flow the cross-sectional through which flow occurs is constant along
the channel and so also is the velocity.Thus y1=y2=yo andV1=V2 =V and the
channel bed, water surface and energy line are parallel to one another.
According to force balance along the direction of flow; we
can write,
PLALFF oτθγ =+− sin21
F1= Pressure force at section 1
F2= Pressure force at section 2
W= Weight of fluid between
section 1 and 2=
So= slope of channel
θ= Inclination of channel
with horizontal line
τo= shearing stress
P= Wetted perimeter
L= length between sections
V= Avg. Flow velocity
yo= depth of flow
ALγ

12. Derivation of Chezy’s formula
12
θγθγ
θγ
τ sinsin
sin
R
P
A
PL
AL
o ===
x
zz
So
∆
−
= 21
( ) ( )
x
yzyz
Sw
∆
+−+
= 2211
( ) ( )
x
h
S
x
gvyzgvyz
S
L
∆
=
∆
++−++
=
2/2/ 222111
θsin=≈= SSS wo
For channels with So<0.1, we can safely assume that
oo RSγτ =
Therefore;

13. Derivation of Chezy’s formula
13
τo (shearing stress) can also be expressed as (already discussed)
2
2
V
Cfo ρτ =
Comparing both equations of τo we get;
o
foo
f
of
RSCV
fCRS
f
g
RS
C
g
V
RS
V
C
=
===
=
4/
82
2
2
Q
γρ
Where C is Chezy’s Constant whose value depend upon the type of
channel surface
f
g
C
8
=Q

14. Relation b/w f and C
14
As f and C are related, the same consideration that are present for
determination of friction factor, f, for pipe flows also applies here.
4/
82
fC
f
g
C
g
C f
f
=== Q

15. Empirical Relations for Chezy’s Constant, C
15
Although Chezy’s equation is quite simple, the selection of a correct value
of C is rather difficult. Some of the important formulae developed for
Chezy’s Constant C are;
1. Bazin Formula: A French hydraulic engineer H. Bazin (1897) proposed
the following empirical formula for C
RK
C
/181
6.157
+
=
R= Hydraulic Radius
K=Bazin Constant
The value of K depends upon the type of channel surface

16. Empirical Relations for Chezy’s Constant, C
16
2. Kutter’s Formula: Two Swiss engineers Ganguillet and Kutter
proposed following formula for determination of C
R= Hydraulic Radius
n=Manning’s roughness
coefficient
3. Manning’s Formula: Rober Manning (An Irish engineer) proposed the
following relation for Chezy’s coefficient C
2/13/21
oSR
n
V =
n= Manning’s Roughness coefficient
( ) 6/1
/1 RnC =
The values of n depends upon nature of channel surface
BG units SI units

17. Empirical Relations for Chezy’s Constant, C
17

18. Relation b/w f and n
18
Since
Also
It mean n and f can also be related with each other.
Hence
4/
82
fC
f
g
C
g
C f
f
=== Q
( ) 6/1
/1 RnC =
g
f
Rn
8
486.1 6/1
=
g
f
Rn
8
6/1
= SI
BG

19. Chezy’s and Manning’s Equations in SI and BG System
19
Chezy’s Equation Manning’s Equation
2/13/21
oSR
n
V =
( ) 2/13/23 1
/ oSAR
n
smQ =
( ) 2/13/2486.1
oSAR
n
cfsQ =
SI
BG
oRSCV =
oRSCAQ =
Value of C is determine from
respective BG or SI Kutter’s
formula.
C= Chezy’s Constant
A= Cross-sectional area of flow A= Cross-sectional area of flow

20. Problem-1
20
Water is flowing in a 2-m-wide rectangular, brick channel (n=0.016) at a
depth of 120 cm.The bed slope is 0.0012. Estimate the flow rate using the
Manning’s equation.
Solution: First, calculate the hydraulic radius
Manning’s equation (for SI units) provides

21. Problem-2
21
Compute the flow rate for a depth of 2, 4, 6 and 8ft.
( ) 2/13/2486.1
oSAR
n
cfsQ =
For BG units

22. 22
Let’s consider a
trapezoidal channel having
bottom width, b, depth of
flow, d, and side slope, S.
Trapezoidal section
h
b
s
Sh Sh
1
( ) 2222
2
22
sec
hShShA/hhShbPimeterWetted Per
ShbhAa of flowtional areCross-
++−=++==
+==
Sh
h
A
b
ShbhA
−=
+= 2
b+2Sh
1Sh 2
+
θ

23. Problem-3
23
Solution
( ) 2/13/23 1
/ oSAR
n
smQ =
For SI units 4
y

24. Problem-4
24
2/13/2486.1
oSR
n
V =
For BG units
6
3

25. Problem-5
25
( ) 2/13/23 1
/ oSAR
n
smQ =
For SI units
321 QQQQ ++=

26. Problem-7
26
( ) 2/13/23 1
/ oSAR
n
smQ =
For SI units
Solution: (a)

27. Problem-7
27
(b) ( ) 2/13/23 1
/ oSAR
n
smQ =For SI units

28. Most Economical Section
28
From Manning’s formula, we can write that
For a given channel of slope, So, area of cross-section, A, and roughness, n,
we can simplify above equation as
It emphasis that discharge will be maximum, when Rh is maximum and for a
given cross-section, Rh will be maximum if perimeter is minimum.
Therefore, the most economical section (also called best section or most
efficient section) is the one which gives maximum discharge for a given area
of cross-section (say excavation for channel shape).
ohSAR
n
Q
1
∝
P
Q
P
A
QRQ h
1
∝⇒∝⇒∝

29. Most economical rectangular section
29
Let’s consider a rectangular
channel as shown in figure in
which width of channel is b and
depth of flow is h.
b
h
2h/A2hbPPerimeterWetted
bhAflowofareasectional-Cross
+=+==
==
h
For most economical section, perimeter should be minimum. i.e.,
( ) ( ) 02h/A2hbP/dh
0P/dh
=+=+=
=
h
dh
d
dh
d
d
d
2/2
2
202
2
2
2
bhorhb
hbh
hA
h
A
==
=
=⇒=+−
Hence for most economical rectangular section,
width is twice the depth of channel

30. Problem
30

31. 31
Let’s consider a trapezoidal
channel having bottom
width, b, depth of flow is d,
and side slope, S, as shown
in figure
Most economical trapezoidal section
h
b
s
Sh Sh
1
( ) 2222
2
hSh2/AhSh2bPPerimeterWetted
ShbhAflowofareasectional-Cross
++−=++==
+==
Shh
For most economical section, perimeter should be minimum. i.e.,
( ) 0hSh2/A0 22
=++−⇒= Shh
dh
d
dh
dP
Sh
h
b −=
+=
A
ShbhA 2
b+2Sh
1Sh 2
+
θ

32. Most economical trapezoidal section
32
Hence for most economical trapezoidal section, top
width is twice the length of one sloping side or half of
top width is equal to length of one sloping side
( ) 01S201S2h/A 2
2
2
=++−−⇒=++− S
h
A
Shh
dh
d
1Sh2Sh2b1Sh
2
Sh2b
1S2
Sh2b
1S2
Shb
1S2
Shb
1S2
Shbh
1S2
22
2
22
2
2
2
2
2
+=+⇒+=
+
+=
+
+=+
+
⇒+=+
+
+=+
+
⇒+=+
h
h
Sh
h
S
h
S
h
S
h
A

33. Most economical trapezoidal section
33
For given width, b, and depth, h, perimeter becomes only the
function of side slope, S,. So if we estimate value of S that provide
minimum P then we have;
( ) ( ) 01S2h/A0hhS2/A0 2222
=++−⇒=++−⇒= Shh
dS
d
Shh
dS
d
dS
dP
( ) ( )
( ) ( ) SSh
ShSh
21Sh21S
01Sh2021S
2
1
2h
22
2/1212/12
=+−⇒=+−
=++−⇒=





×++−
−−
Squaring both sides of equation, we get
3
1
3
1
41S 222
=⇒=⇒=+− SSS
If sloping sides make an angle θ with the horizontal than S=tanθ
o
S 60
3
1
tan =⇒== θθ

34. Thank you
Questions….
Feel free to contact:
34