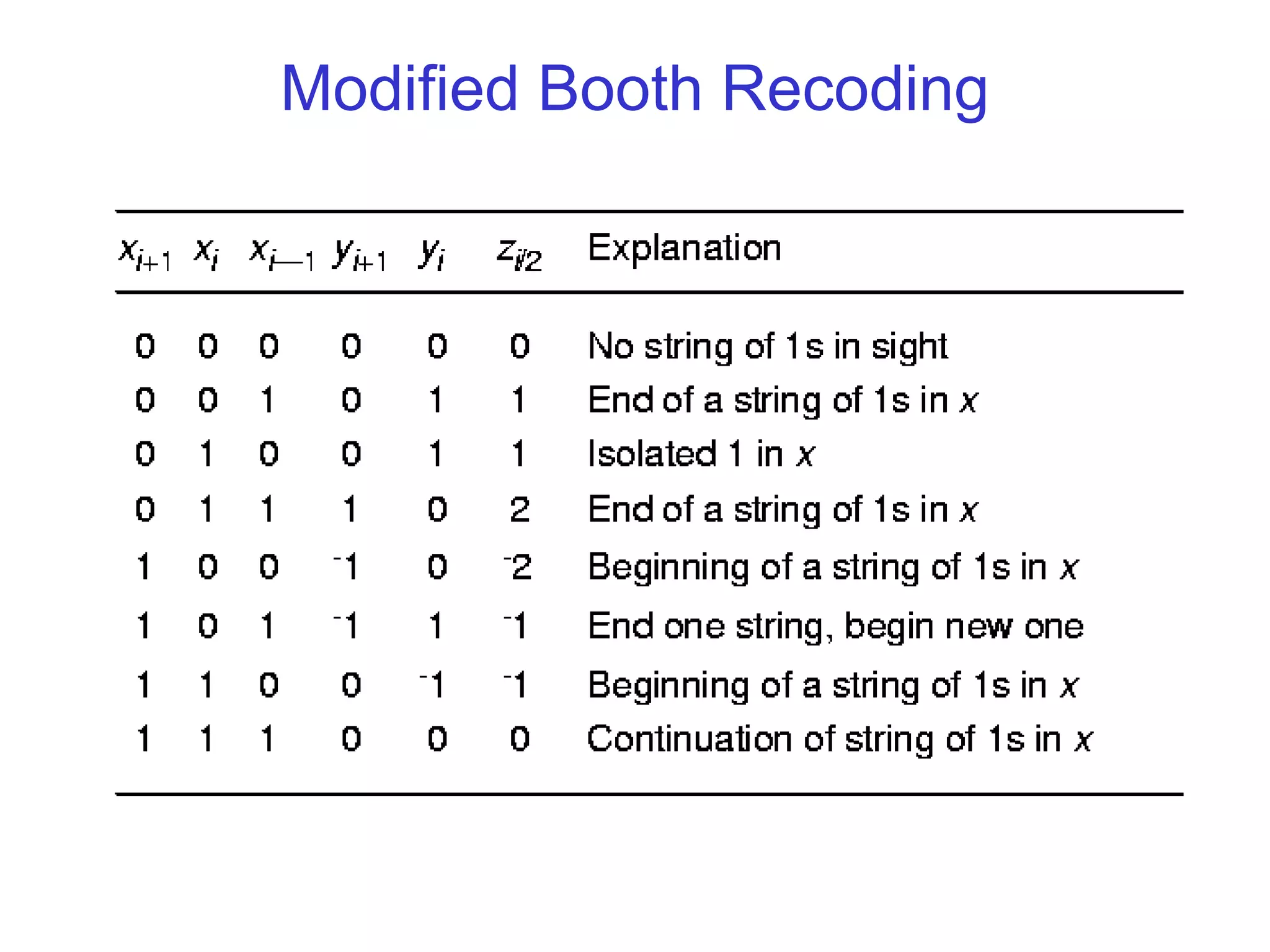
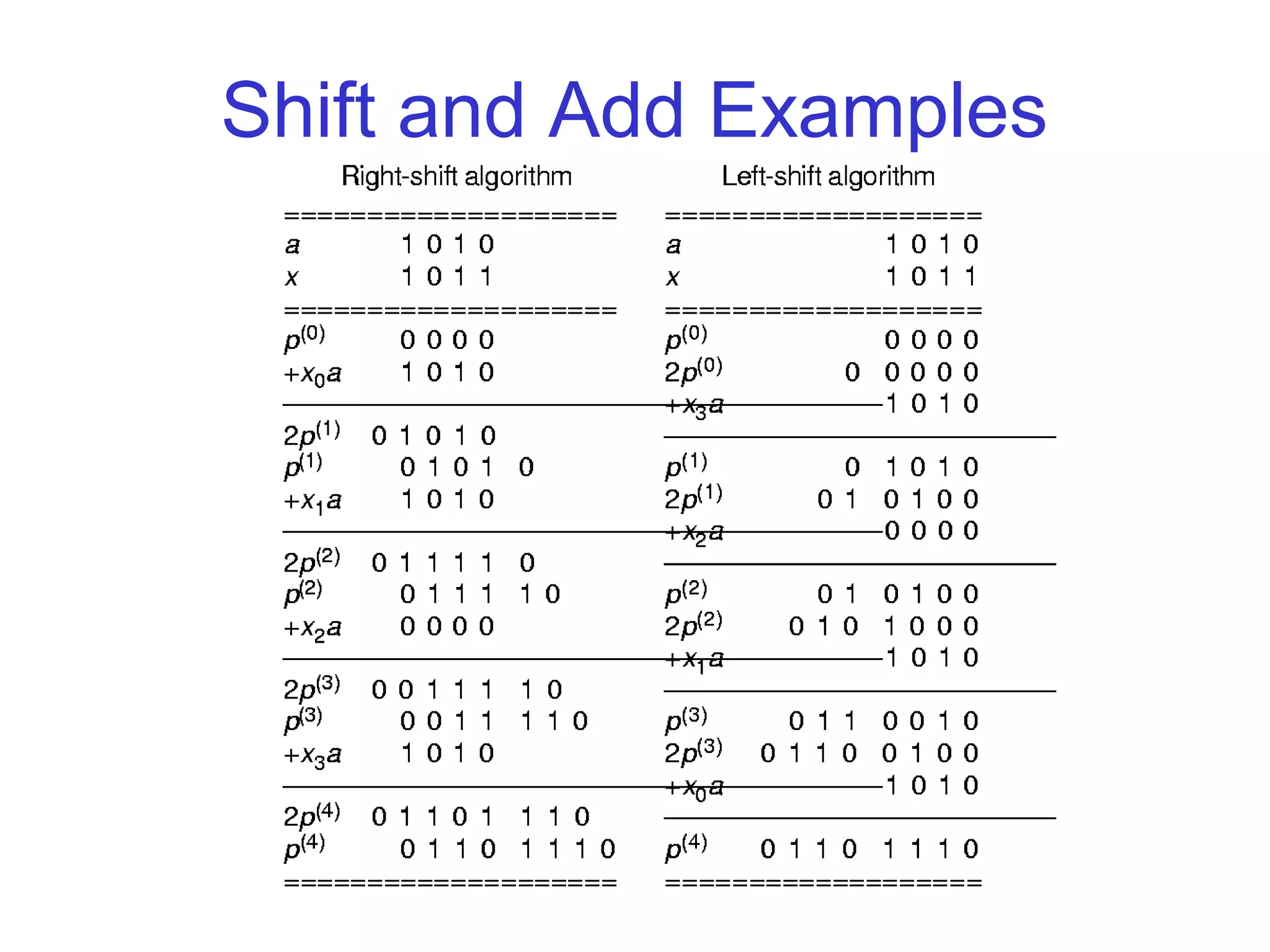
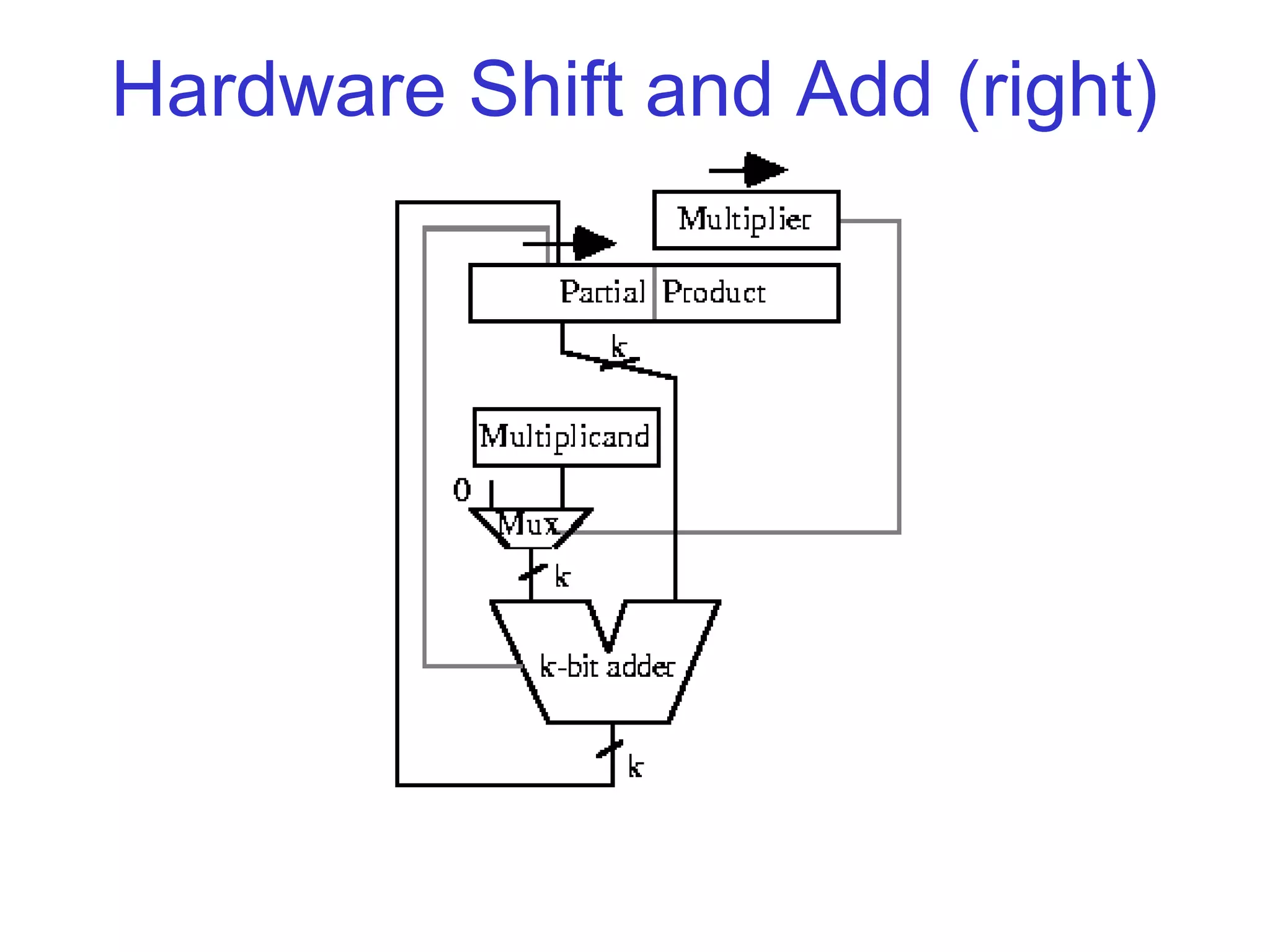
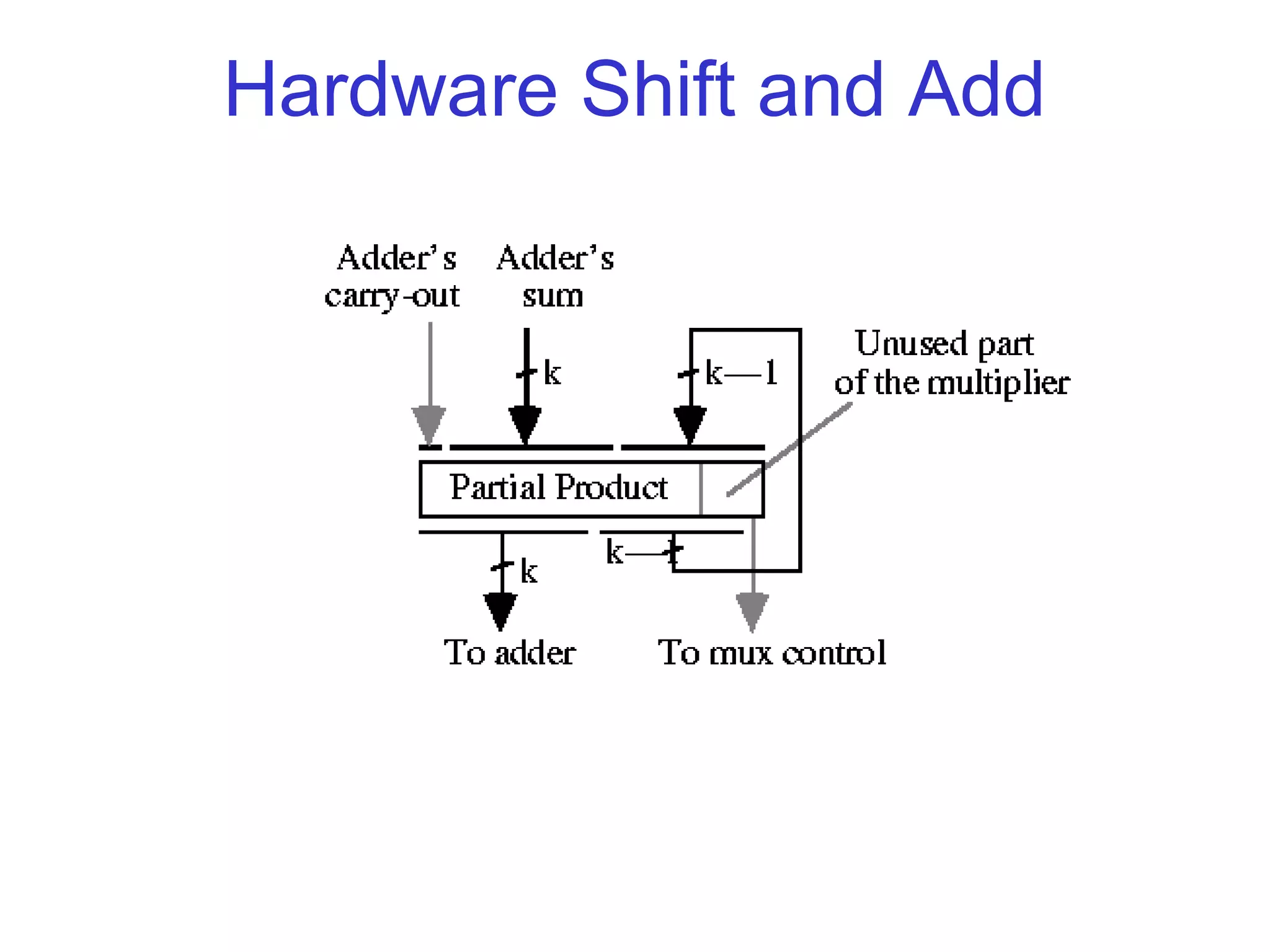
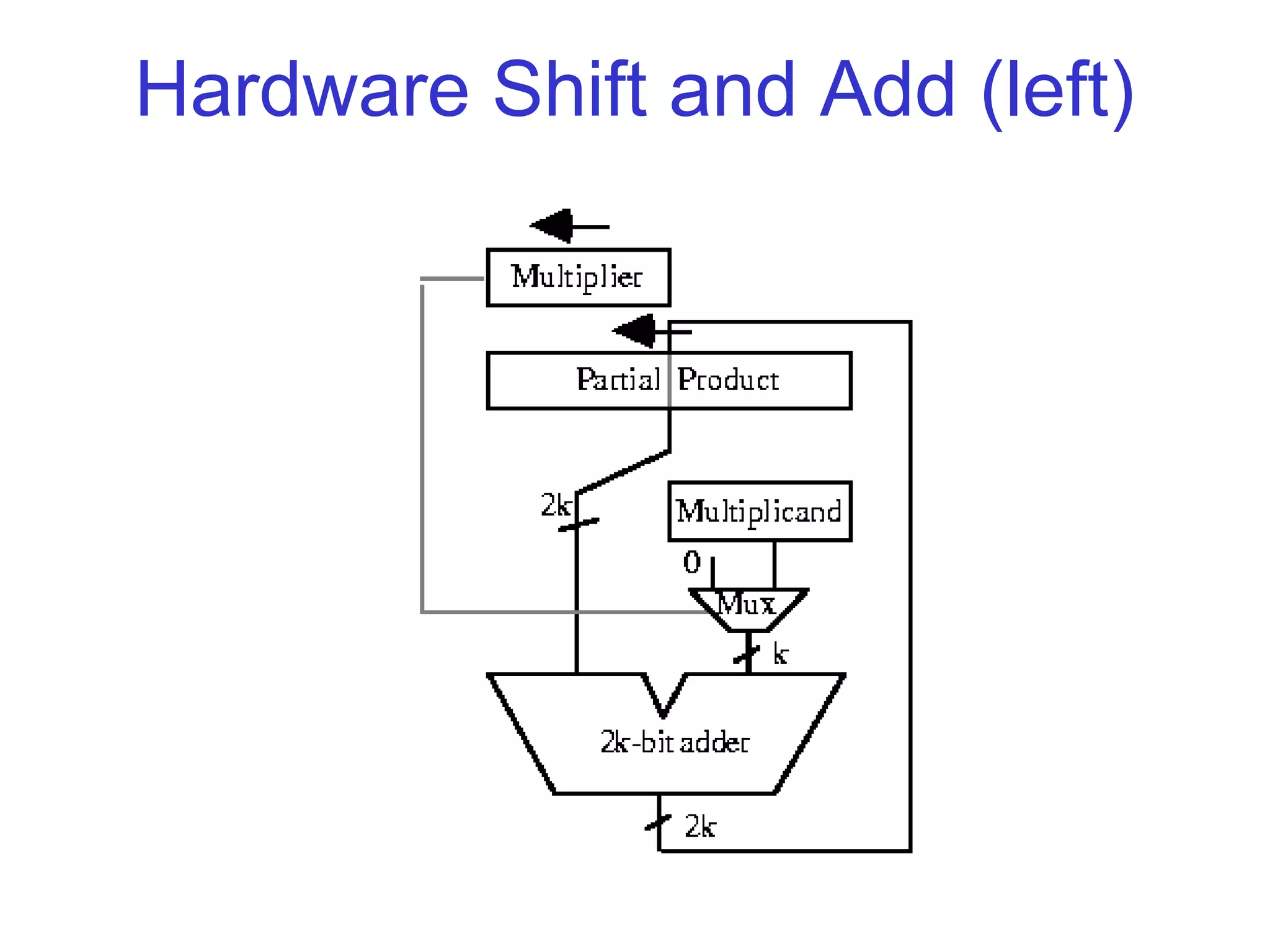
The document discusses various techniques for accelerating the multiplication process, including shift-and-add, Booth's recoding, and higher radix multipliers. Booth's recoding maps digit sets to [-1,1] to skip additions when partial products are zero. Modified Booth's recoding improves on this by considering three adjacent bits to encode multipliers into [-2,2], allowing the use of radix-4 grouping to reduce the number of partial product additions. Modern multipliers apply Modified Booth's Recoding to take advantage of its higher radix structure.

1. Multiplication

2. Multiplier Notation
Partial Products
Logical-AND

3. Shift and Add Paradigm

4. Shift and Add Examples

5. Programmed Multiplication

6. Programmed Multiplication (cont.)

7. Hardware Shift and Add (right)

8. Hardware Shift and Add

9. Hardware Shift and Add (left)

10. Signed Number Multiplication
(positive case)

11. Signed Number Multiplication
(negative case)

12. Booth’s Recoding (or encoding)
• Developed for Speeding Up Multiplication in Early Computers
• When a Partial Product of 0 Occurs, Can Skip Addition and
Just Shift
• Doesn’t Help Multipliers Where Datapaths Go Through Adder
Such as Previous Examples
• Does Help Designs for Asynchronous Implementation or
Microprogramming Since Shifting is Faster Than Addition
• Variable Delay – Depends on Number of One’s in
• Booth Observed that a String of 1’s May be Replaced as:
j −1 i +1 j +1
2 +2
j
+L+ 2 +2 =2
i
−2 i

13. Booth’s Recoding Example
xn xn-1 ... xi xi-1 ... x0 (0)
yi=xi-1 - xi
yn ... yi ... y0
xi xi-1 Operation Comments yi
0 0 shift only string of zeros 0
1 1 shift only string of ones 0
1 0 subtract shift beg. string of ones -1
0 1 addition shift end string of ones 1
EXAMPLE
0011110011(0)
0100010101

14. Booth’s Recoding
• Maps Words With Digit Set [0,1] to Those With [-1,1]

15. Sequential Multiplication
A 1011 (-510)
X 1101 (-310)
Y 0111 (recoded)
(-1) Add –A 0101
Shift 00101
(+1) Add +A 1011
11011
Shift 111011
(-1) Add –A 0101
001111
Shift 0001111 (+1510)

16. Booth Multiplier Example

17. Booth’s Recoding Drawbacks
• Number of add/sub Operations are Variable
• Some Inefficiencies
EXAMPLE
001010101(0)
011111111
• Can Use Modified Booth’s Recoding to Prevent
• Will Look at This in Later Class

18. Sign Extension
• Consider 6-bit 2’s Complement Number
s=0 Positive Value; s=1 Negative Value
• Show Sign Extension Works:
s s s s s p4 p3 p2 p1 p0
= − s ×29 + s ×28 + s ×27 + s ×26 + s ×25 + p4 ×24 + p3 ×23 + p2 ×2 2 + p1 ×21 + p0 ×20
4
= − s ×2 + s ×(2 + 2 + 2 + 2 ) + ∑ pi ×2i
9 8 7 6 5
i =0
4
= − s ×2 + s ×(2 − 2 ) + ∑ pi ×2i
9 9 5
i =0
4
= − s ×2 + ∑ pi ×2i
5
i =0
• Definition of 2’s Complement

19. Sign Extension Example
A 010110 (+2210)
X 001011 (+1110)
Y 010101 (recoding)
11111101010 (neg. A)
0000000000 (0 A)
111101010 (neg. A)
00000000 (0 A)
0010110 (neg. A)
000000 (0 A)
00011110010 (24210)

20. Sign Extension Example
• Same Trick as Before, Complement Original Sign Bit
• Add 1 to Column 5
1
001010 (neg. A)
100000 (0 A)
001010 (neg. A)
100000 (0 A)
110110 (neg. A)
100000 (0 A)
00011110010 (24210)

21. Methods for Fast Multiplication
• Reduce Number of Partial Products to be Added
– Group Multiplier Bits Together
– Higher Radix Multiplier
• Add the Partial Products Faster

22. Radix-r Shift and Add

23. Radix-4 Multiplication
• Shifter is Multi-bit
• No Longer a Simple AND of xi with a
• Need 4:1 MUX with 0, a, 2a, 3a as Inputs

24. Partial Product Selection
• 0, a and 2a are easy
• 3a=a+2a → Requies an Adder!
• Need a Way to Compute 3a Efficiently

25. Example With 3a Availability

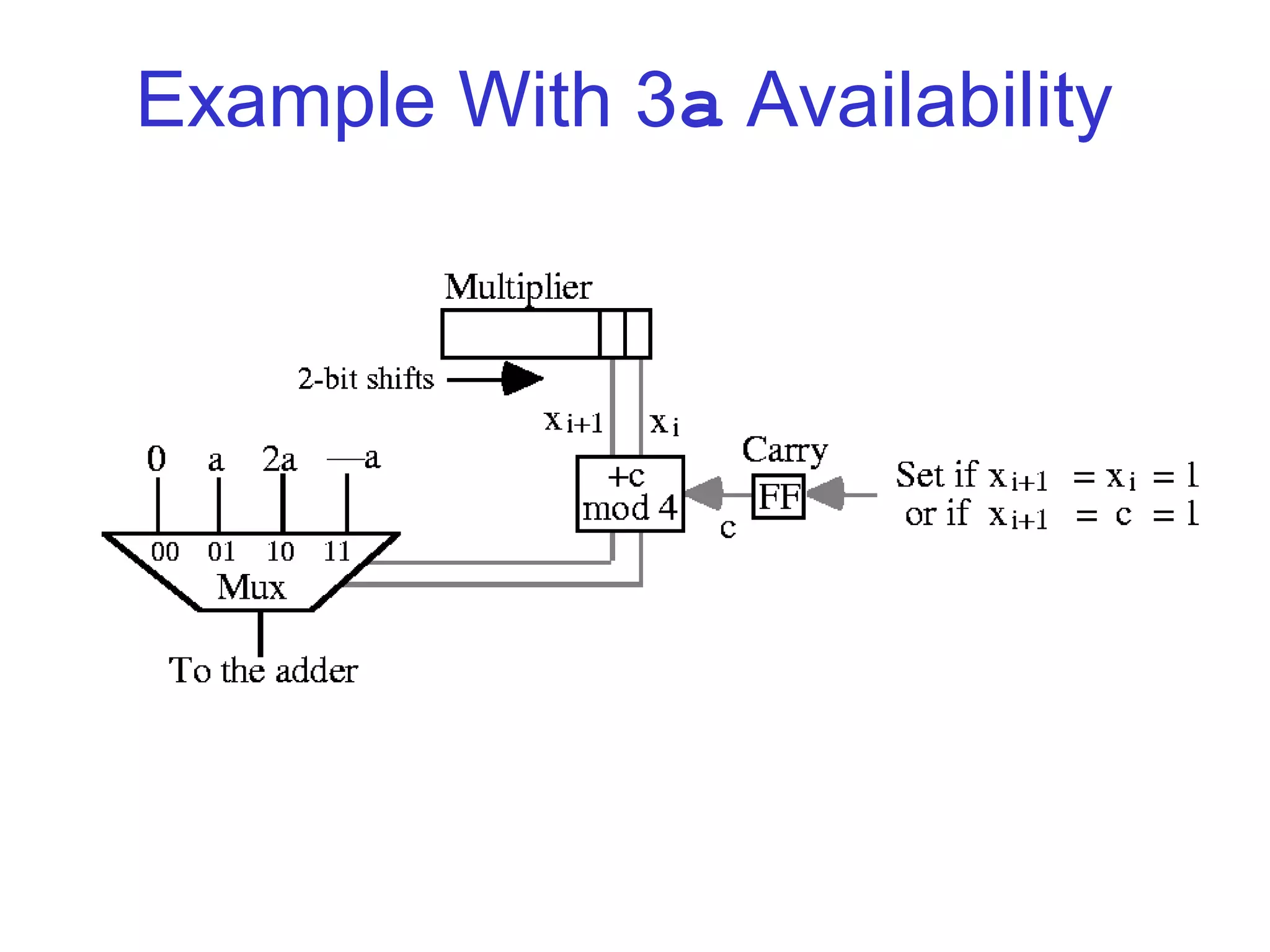
26. Computing 3a
• One Way is to Precompute 3a and Store in Register Initially
• Another Way is When 3a Occurs Add -a
• Send Carry of 1 to Next into Next Radix-4 Digit of Multiplier
• Causes Incoming Multiple to be [0,4] Versus [0,3]
– 4 Because incoming carry to 112 Causes Digit 1002
• Multiples 0, 1, 2 Handled Easily
• Multiple 3 Converted to –1 With Outgoing Carry of 1
• Multiple 4 Converted to 0 With Outgoing Carry of 1
• Requires Extra Cycle of Computation Since MSD May Have Carry

27. Example With 3a Availability

28. Using Radices >4
• Could Also Use Radices of 8, 16, ...
• Bit Groupings of Size 3, 4, ...
• Multiple Generation Hardware Becomes More Complex
• Must Precompute 3a, 5a, 7a, ....
• Or Use 3a With a Carry Scheme
• Carry Scheme Converts Multipliers 5a, 6a, 7a
to –3a, -2a, -a, etc.
• Carry Digit in This Form Becomes a 1

29. Booth Recoding
• Modern Arithmetic Circuits DO NOT Apply
Booth Recoding Directly
• Useful in Understanding Higher-radix Versions of
Booth Recoding
• No Consecutive 1’s or –1’s Occur Using Previously Seen
Booth Recoding
• Booth Recoding in Radix-4 Results in the Following:
– Only Multiples of ±a or ±2a are Required
– These are Easily Obtained Using Shifting and Complementation

30. Modified Booth Recoding
• Booth Recoding Results From xi and xi-1
• Radix-4 Multiplier Digits Implies Booth Recoding
Based on xi+1, xi and xi-1
• Similar to Classical Booth Recoding, Modified Booth
Recoding Encodes Multipliers into [-2,2]

31. Modified Booth Recoding

32. Example Modified Booth Recoding

33. Example Multiplication with MBR

34. Hardware MBR Example