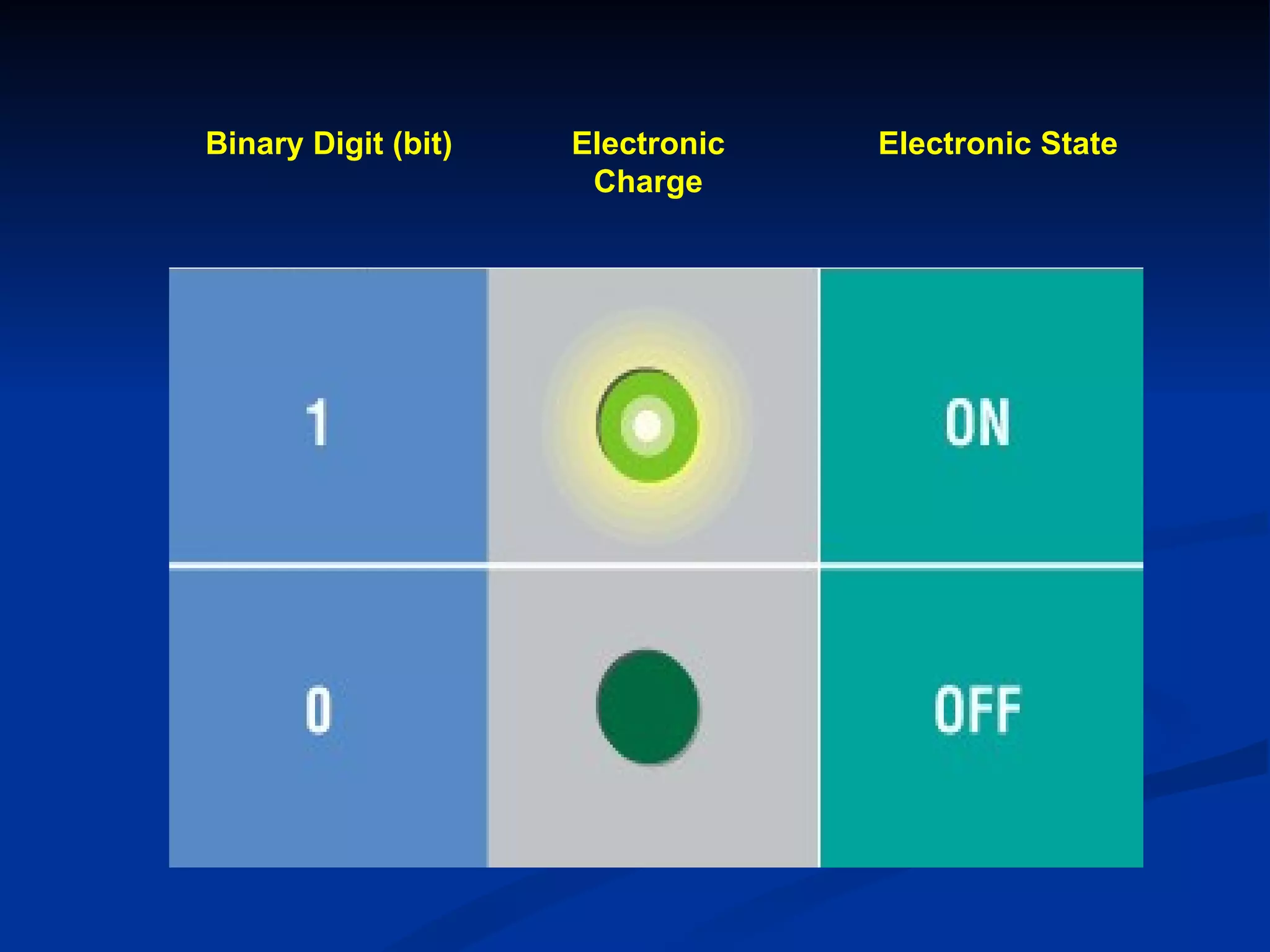
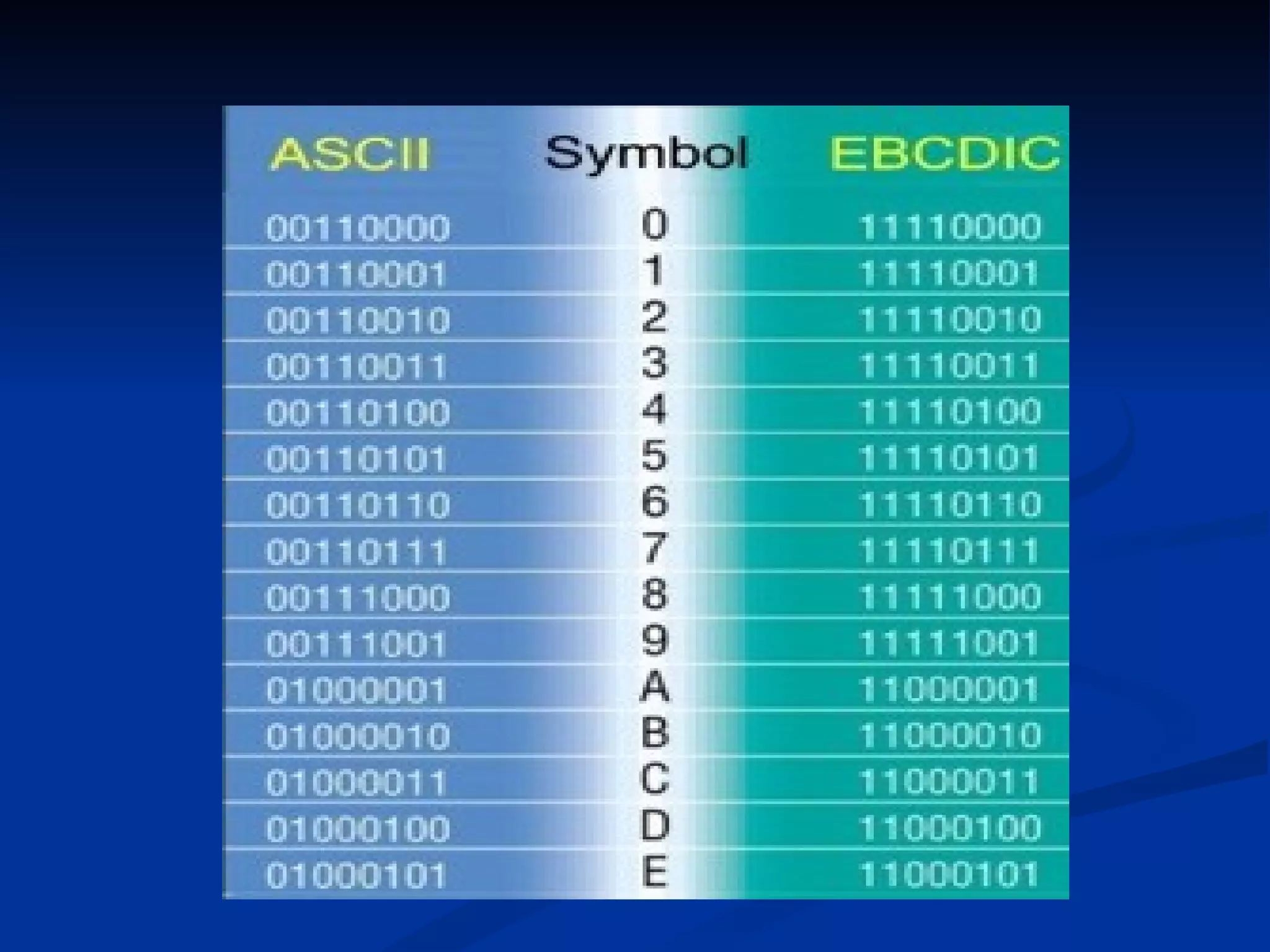
This document discusses how computers represent and process data. It covers: 1) Computers use binary digits (bits) to represent data, with each bit being either 1 or 0 to represent an on or off state. 2) Eight bits are grouped together to form a byte, which can represent individual characters. 3) There are different coding systems like ASCII to represent characters and numbers with binary codes. 4) Data entered from keyboards is converted to binary codes and stored in memory for processing before being converted back to characters on output devices.

1. Data Representation
(in computer system)

2. Data Representation
How do computers represent
data?
a Most computers are digital
• Recognize only two discrete
states: on or off
• Computers are electronic
devices powered by
electricity, which has only
two states, on or off

3. on 1 1 1 1 1
off
0 0 0 0 0

4. Data Representation
What is the binary system?
a A number system that has just two unique
digits, 0 and 1
• A single digit is called a bit (binary digit)
• A bit is the smallest unit of data the
computer can represent
• By itself a bit is not very informative
a The two digits represent the two off and
on states

5. Binary Digit (bit) Electronic Electronic State
Charge

6. Data Representation
What is a byte?
a Eight bits are grouped
together to form a byte
a 0s and 1s in each byte are
used to represent individual
characters such as letters of
the alphabet, numbers, and
punctuation

7. 8-bit byte for the number 3
8-bit byte for the number 5
8-bit byte for the capital letter T

8. Data Representation
What are two popular coding systems
to represent data?
a American Standard Code for
Information Interchange (ASCII)
a Extended Binary Coded Decimal
Interchange Code (EBCDIC)
• Sufficient for English and Western
European languages
• Unicode often used for others

10. Data Representation
How is a character sent from the
keyboard to the computer?
Step 1:
The user presses the letter T key on the keyboard
Step 2:
An electronic signal for the letter T is sent to the system unit
Step 3:
The signal for the letter T is converted to its ASCII binary code
(01010100) and is stored in memory for processing
Step 4:
After processing, the binary code for the letter T is converted to an
image on the output device

12. Decimal to Binary Conversions
•In an earlier slide, we said that every integer value can
be represented exactly using any radix system.
•You can use either of two methods for radix a
conversion: the subtraction method and the division
remainder method.
The subtraction method is more intuitive, but
cumbersome. It does, however reinforce the ideas
behind radix mathematics.
The division method employs the idea that
successive division by a base is equivalent to
successive subtraction by powers of the base.

13. Decimal to D
Binary Conversions
•Fractional decimal values have nonzero digits
to the right of the decimal point.
•Fractional values of other radix systems have
nonzero digits to the right of the radix point.
•Numerals to the right of a radix point represent
negative powers of the radix:
0.4710 = 4 × 10 -1 + 7 × 10 -2
0.112 = 1 × 2 -1 + 1 × 2 -2
= ½ + ¼
= 0.5 + 0.25 = 0.75

14. Decimal to Binary Conversions
•As with whole-number conversions, you can
use either of two methods: a subtraction
method and an easy multiplication method.
•The subtraction method for fractions is
identical to the subtraction method for whole
numbers. Instead of subtracting positive powers
of the target radix, we subtract negative powers
of the radix.
•We always start with the largest value first, n -1,
where n is our radix, and work our way along
using larger negative exponents

15. Decimal to Binary Conversions
•HoweverThe binary numbering system is the
most important radix system for digital
computers.
•, it is difficult to read long strings of binary
numbers-- and even a modestly-sized decimal
number becomes a very long binary number.
For example: 110101000110112 = 1359510
•For compactness and ease of reading, binary
values are usually expressed using the
hexadecimal, or base-16, numbering system.

16. Decimal to Binary Conversions
•The hexadecimal numbering system uses the
numerals 0 through 9 and the letters A through F.
The decimal number 12 is C16.
The decimal number 26 is 1A16.
•It is easy to convert between base 16 and base
2, because 16 = 24.
•Thus, to convert from binary to hexadecimal, all
we need to do is group the binary digits into
groups of four.
A group of four binary digits is called a hextet

17. Decimal to Binary Conversions
•Using groups of hextets, the binary number
110101000110112 (= 1359510) in hexadecimal is:
•Octal (base 8) values are derived from
binary by using groups of three bits (8 = 23):
Octal was very useful when computers used six-bit
words

18. Signed Integer Representation
•Several representations exist for negative values:
Sign Magnitude One's Complement Two's
Complement
000 = +0 000 = +0 000 = +0
001 = +1 001 = +1 001 = +1
010 = +2 010 = +2 010 = +2
011 = +3 011 = +3 011 = +3
100 = -0 100 = -3 100 = -4
101 = -1 101 = -2 101 = -3
110 = -2 110 = -1 110 = -2
111 = -3 111 = -0 111 = -1

19. Signed Integer Representation

20. •Given a full adder (FA), we can use it to
add binary digits (up to 3)
A B carry_in carry_out S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0

21. Signed Integer Representation
• Several FA's can be used to add binary numbers
by feeding out the carry_out one FA to the carry_in
of the FA of the left.
add/sub
B31 B2 B1 B0
A31 A2 A1 A0
1-bit 1-bit 1-bit 1-bit
C32 FA C31 C3 FA C2 FA C1 FA C0
S31 S2 S1 S0
32-bit Ripple Carry Adder/Subtractor (Better: Carry Lookahead Adder)
Note: add/sub is ON (1) if we want A-B, otherwise is OFF

22. •Booth’s algorithm
-Multiplier and multiplicand are placed in
registers Q & M
-Q-1, 1-bit register placed to the right of Q0
Initialize A (third register) and Q-1 to 0
Do n times (n is the number of bits in Q):
If Q0Q-1 = 01 then A <-- A + M
If Q0Q-1 = 10 then A <-- A – M
Arithmetic shift right A, Q, Q-1