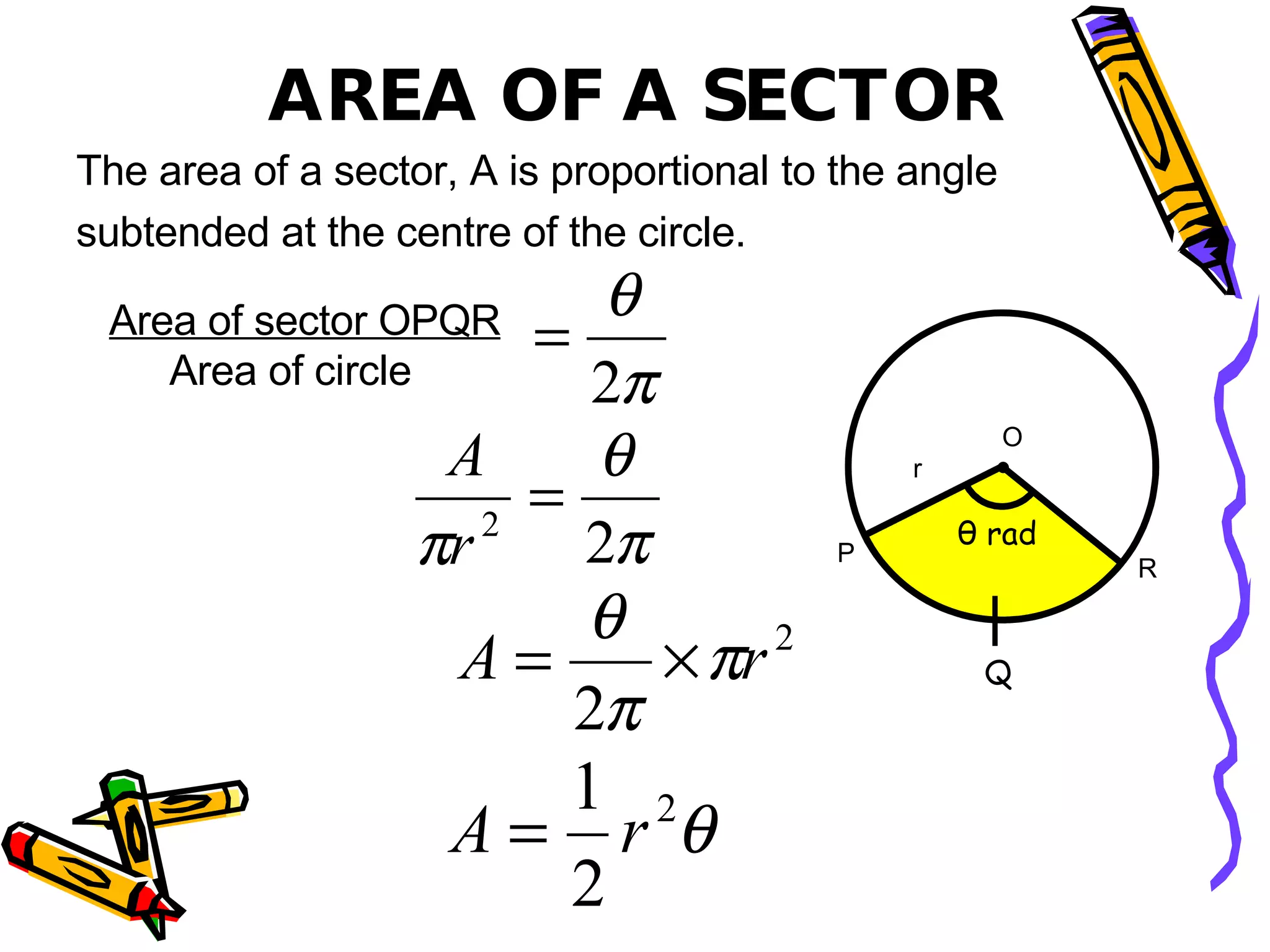
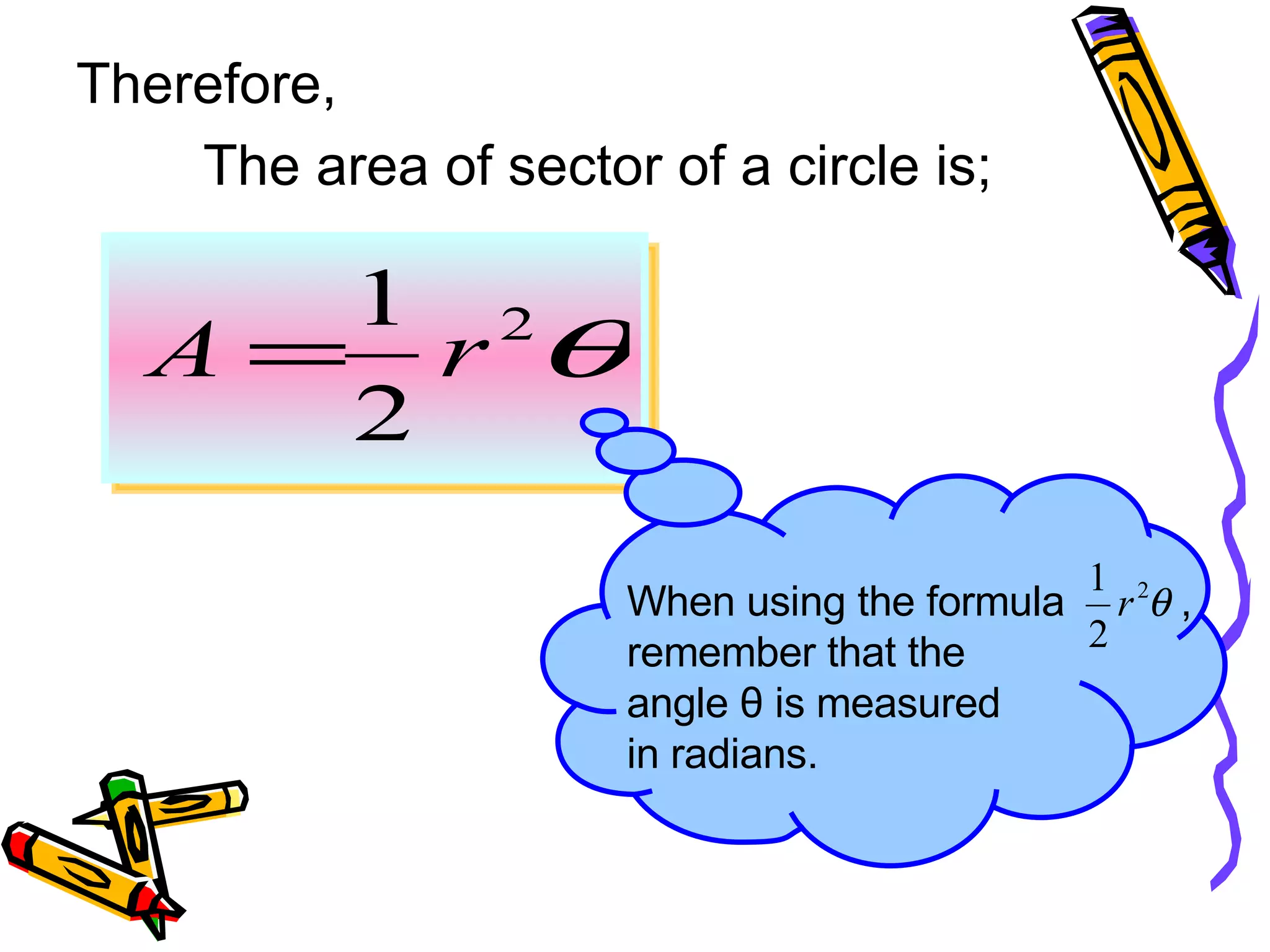
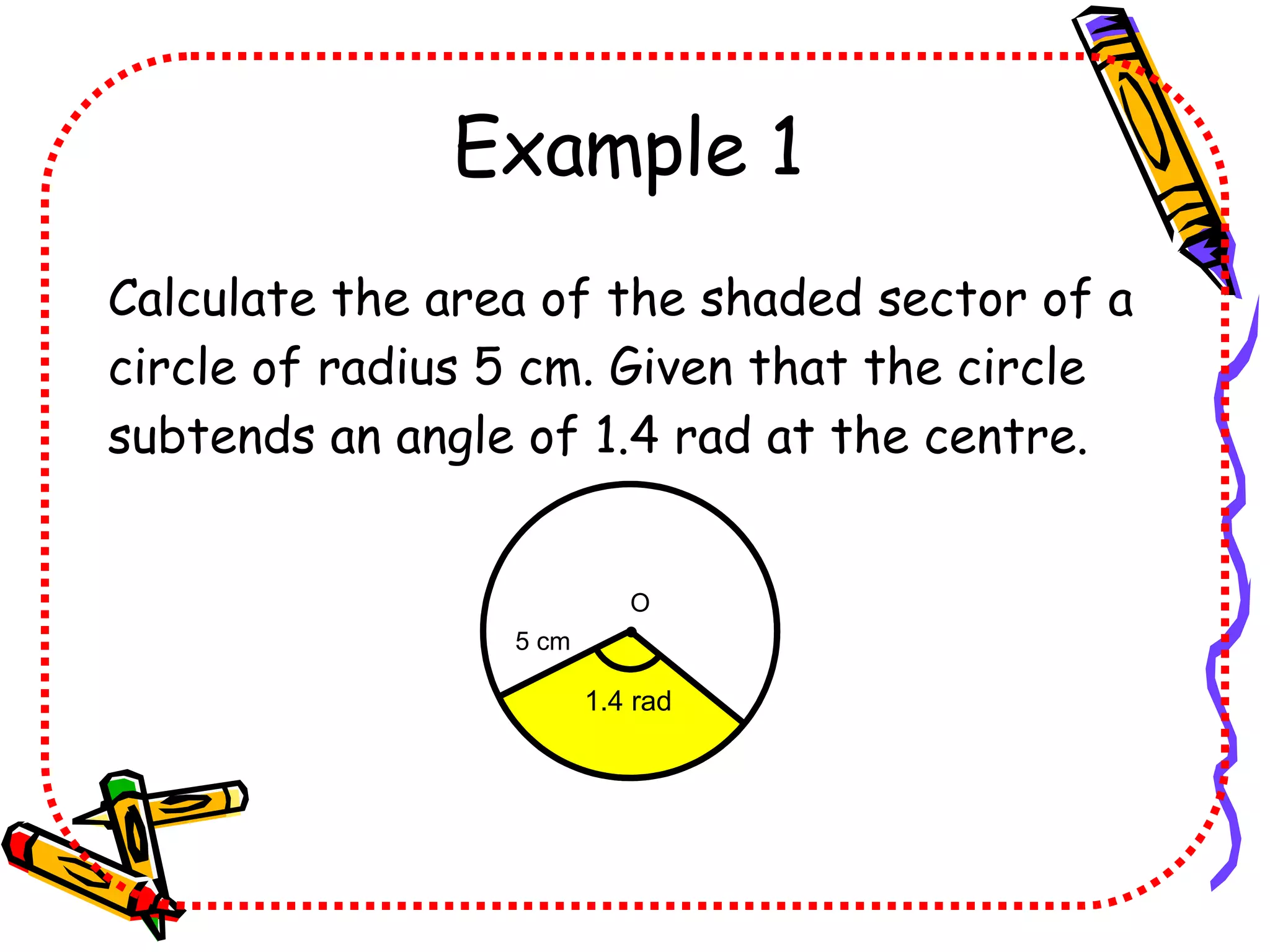
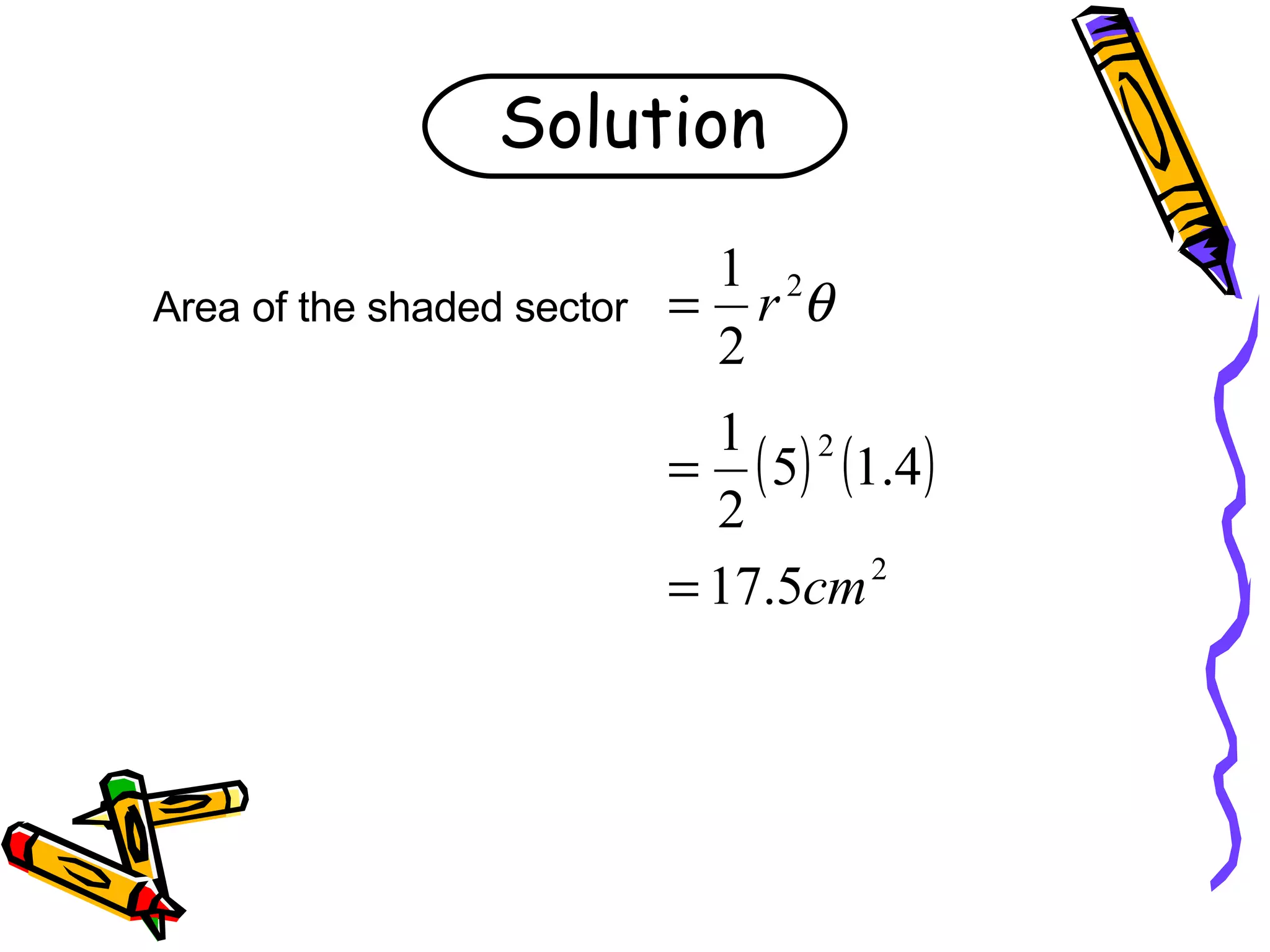
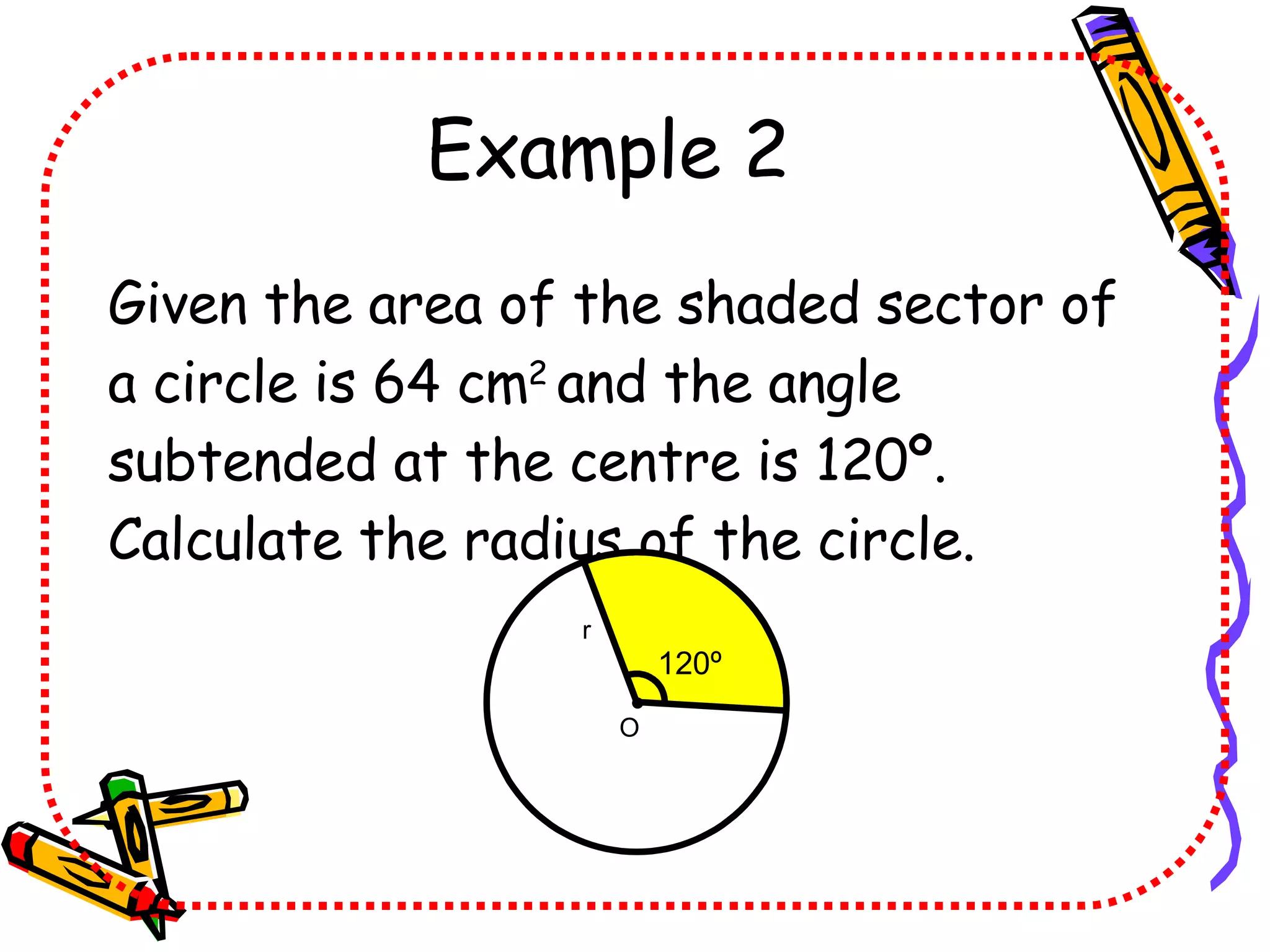
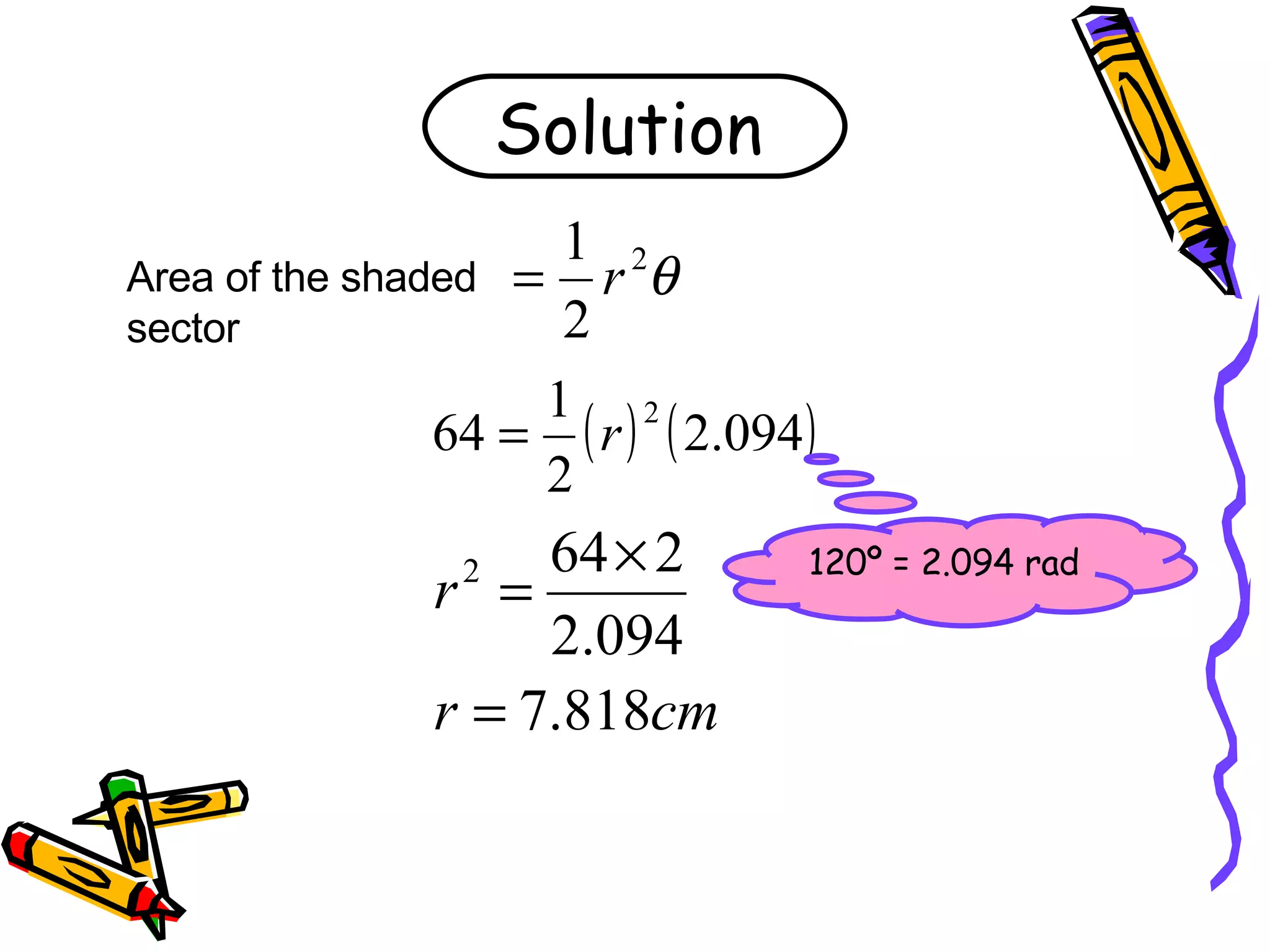
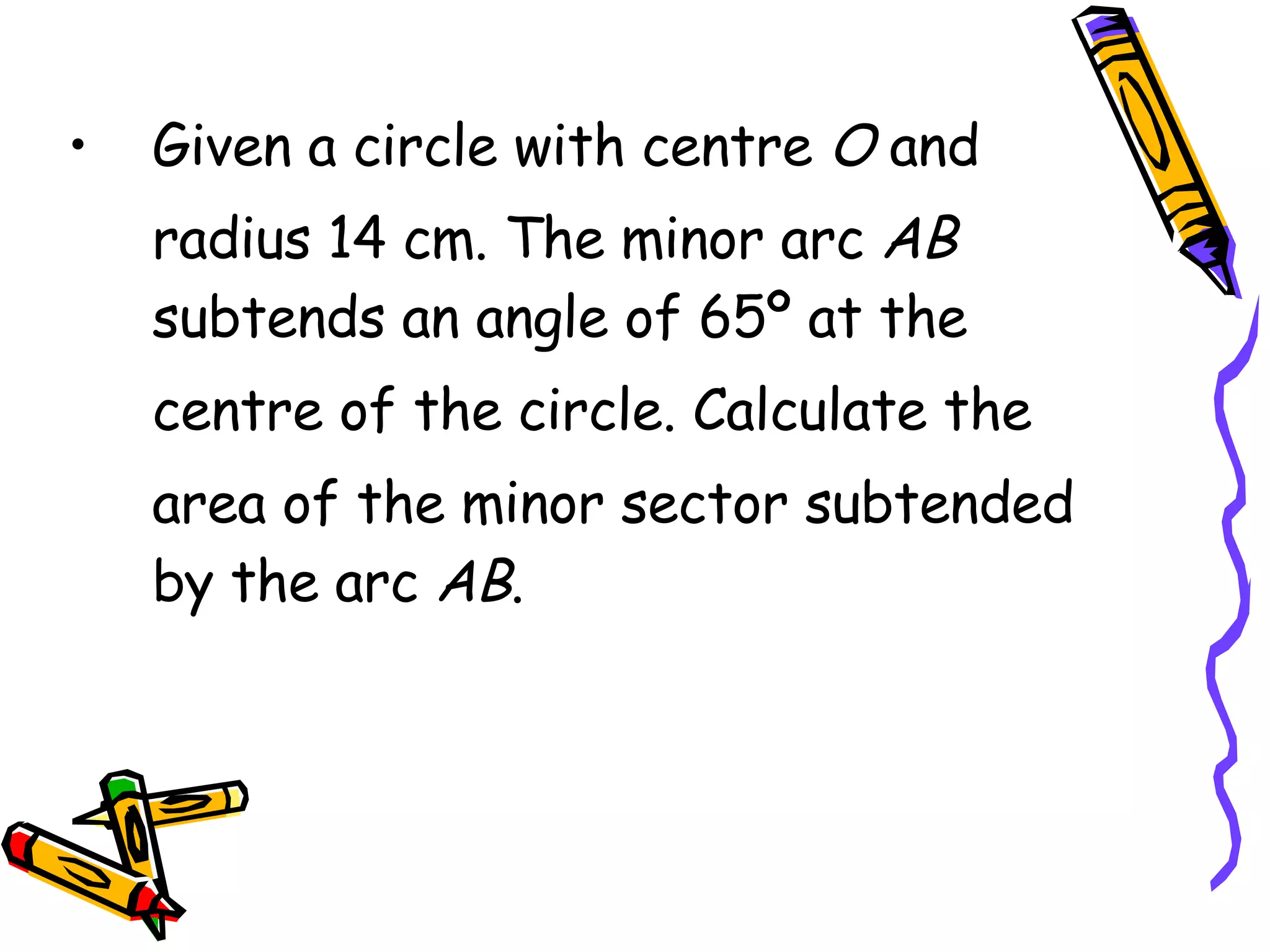
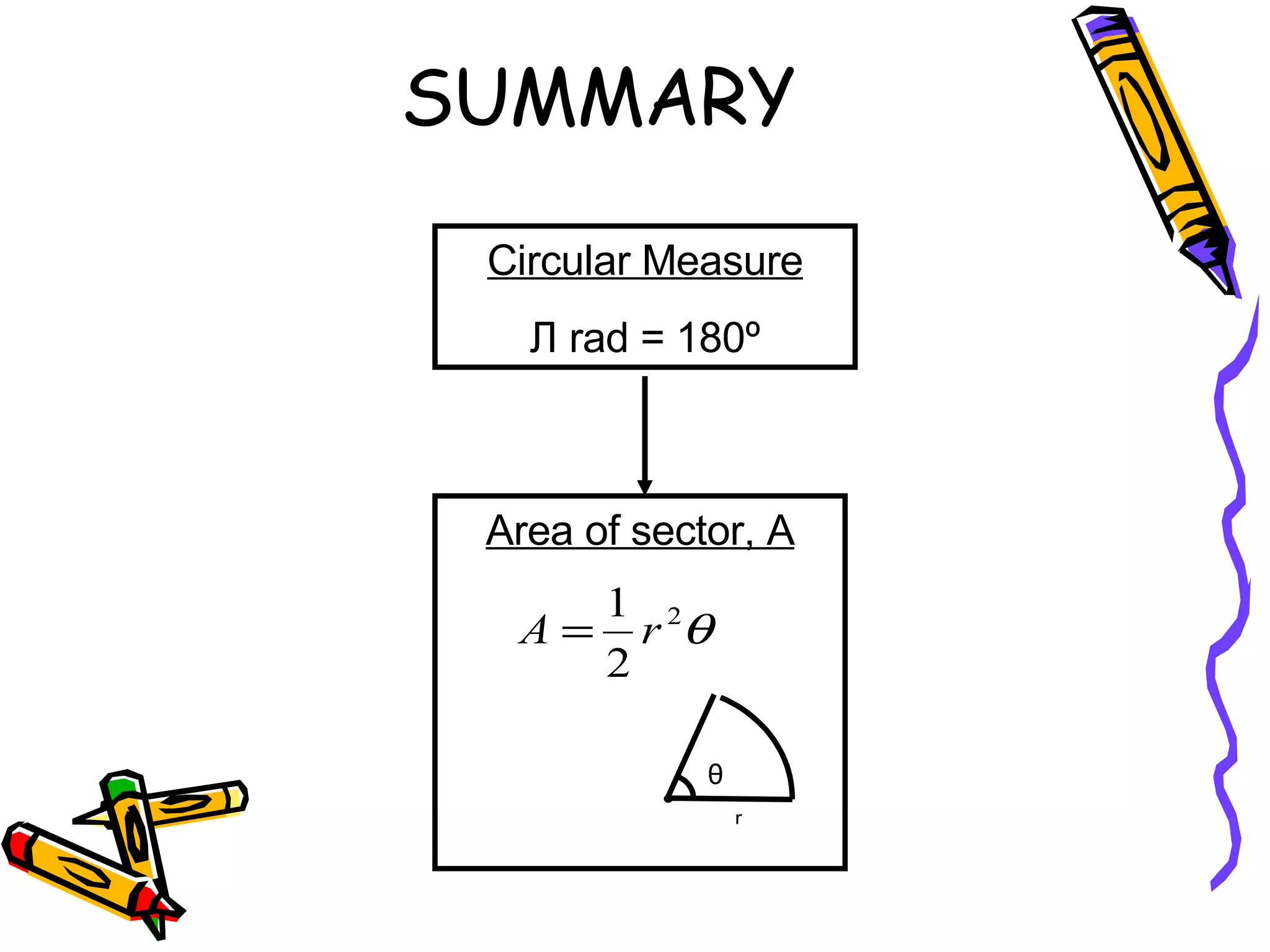
This document discusses calculating the area of a sector of a circle. It provides the formula for finding the area of a sector, which is (θ/360)πr^2, where θ is the central angle in radians and r is the radius. It includes examples of using the formula to find the area, radius, or central angle given two of the three values. It also provides a worksheet with areas and radii of sectors to calculate the missing central angles.

1. SUBTOPIC 8.3: AREA OF SECTOR OF A CIRCLE CHAPTER 8: CIRCULAR MEASURE

2. The net of a cone consists of a circle and a sector.

3. Area of sector OPQR Area of circle AREA OF A SECTOR The area of a sector, A is proportional to the angle subtended at the centre of the circle. θ rad Q

4. Therefore, The area of sector of a circle is; When using the formula , remember that the angle θ is measured in radians.

5. Example 1 Calculate the area of the shaded sector of a circle of radius 5 cm. Given that the circle subtends an angle of 1.4 rad at the centre. 1.4 rad

6. Solution Area of the shaded sector

7. Example 2 Given the area of the shaded sector of a circle is 64 cm 2 and the angle subtended at the centre is 120º. Calculate the radius of the circle. 120 º

8. Solution Area of the shaded sector 120º = 2.094 rad

9. Example 3 Given that the area of the shaded sector of a circle is 80 cm 2 and the radius is 6.5 cm. Find the central angle, θ , in radian. θ

10. Solution Area of the sector

11. WORKSHEET

12. Given a circle with centre O and radius 14 cm. The minor arc AB subtends an angle of 65º at the centre of the circle. Calculate the area of the minor sector subtended by the arc AB .

13. 2. Complete the table below, given the areas and the radii of the sectors and angles subtended. 8 cm 145 cm 2 1.778 rad 200 cm 2 6.5 cm 18л cm 2 θ = 1.64 rad 72 cm 2 50º 38.12 cm 9.15 cm 90 cm 2 Angle subtended, θ Radius, r Area of sector, A

14. SUMMARY Circular Measure Л rad = 180º Area of sector, A θ