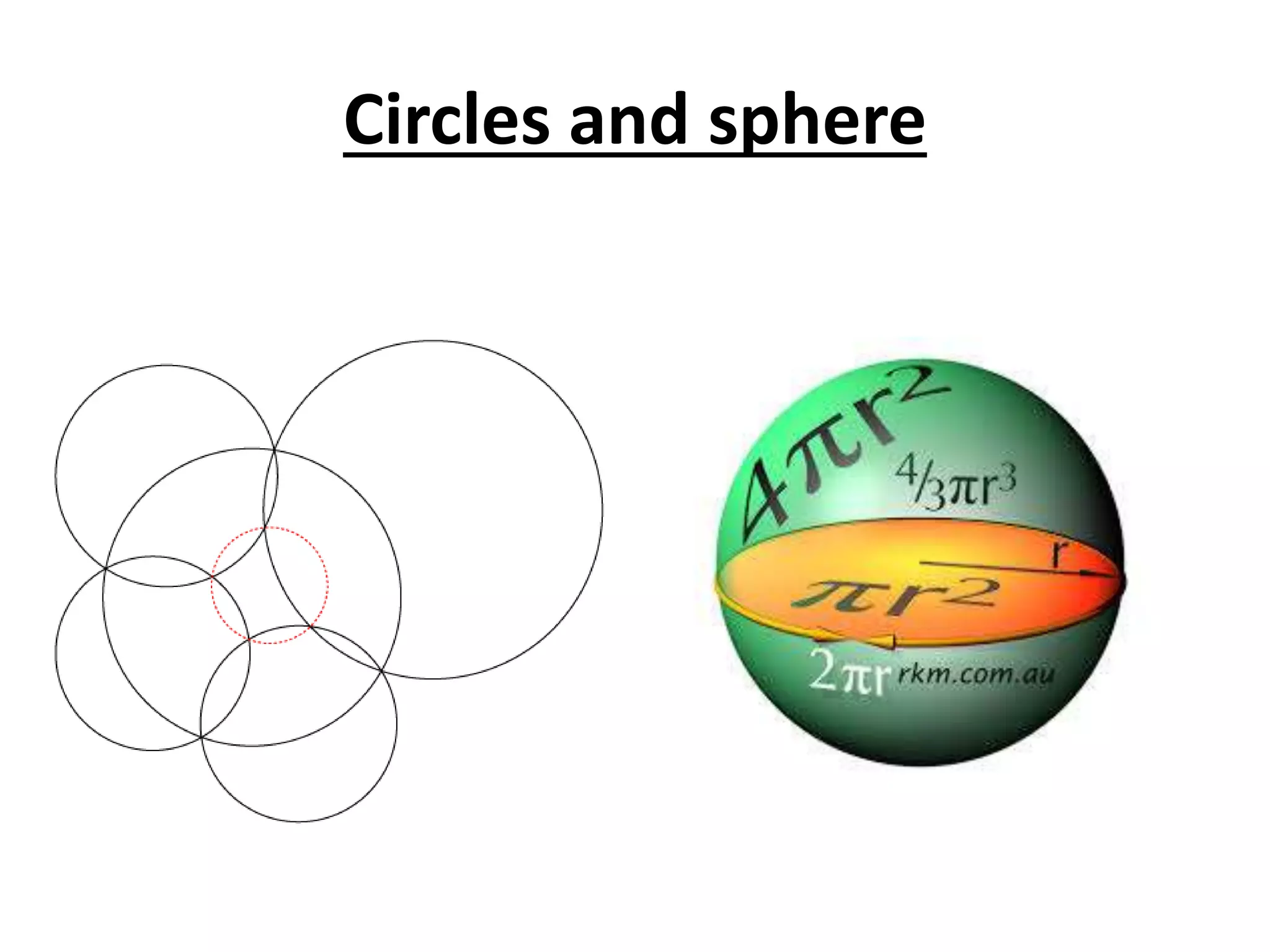
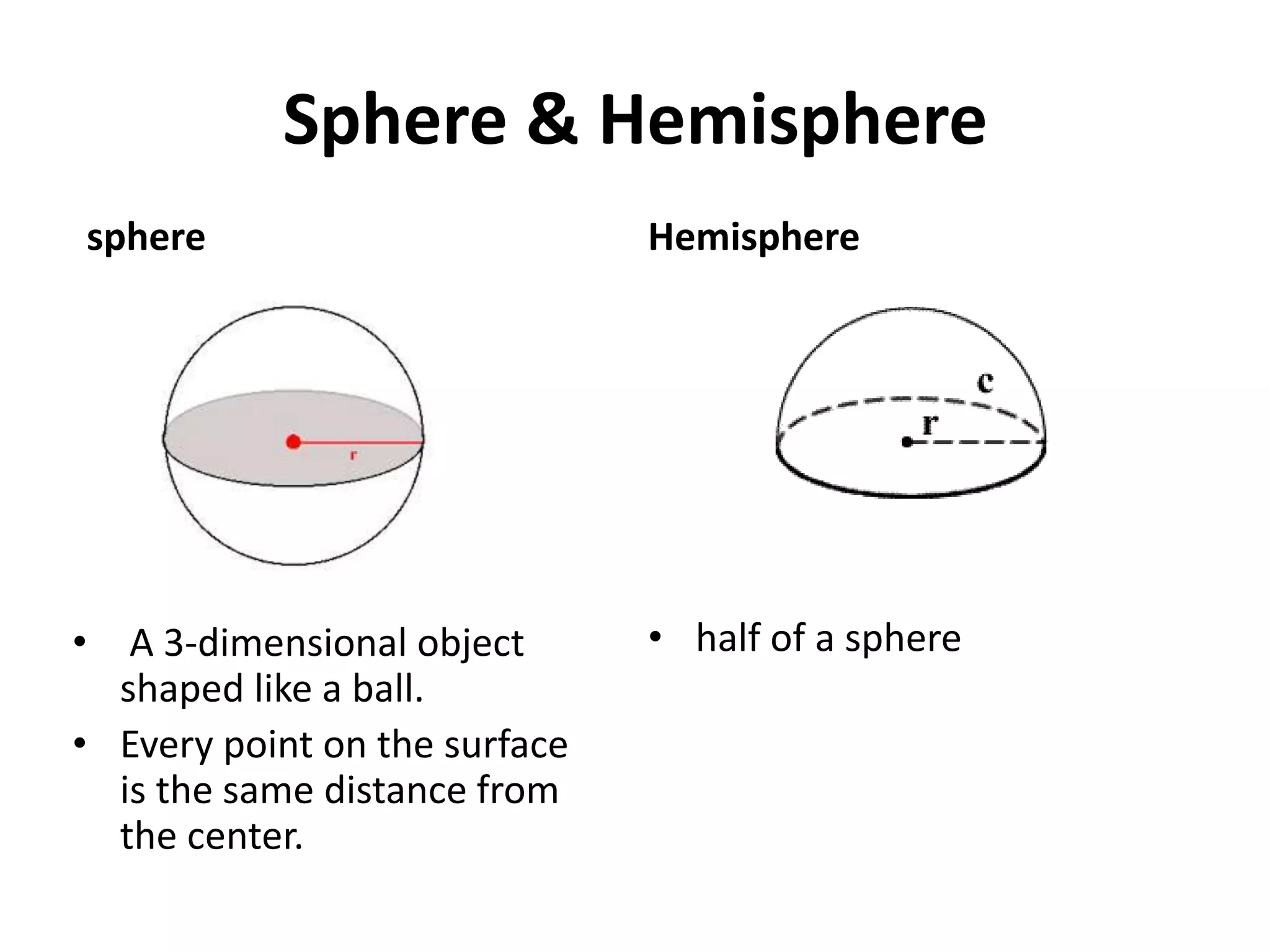
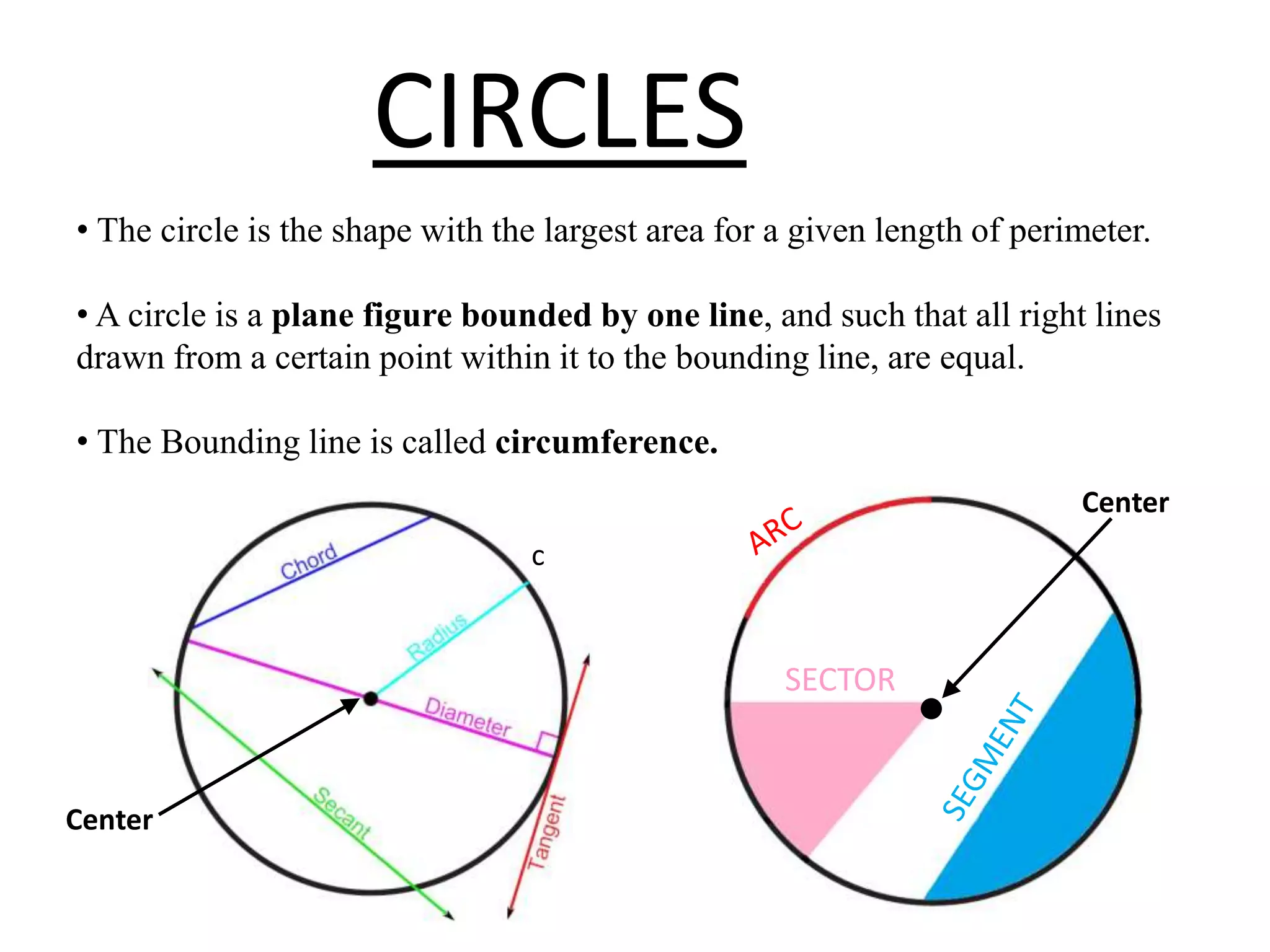
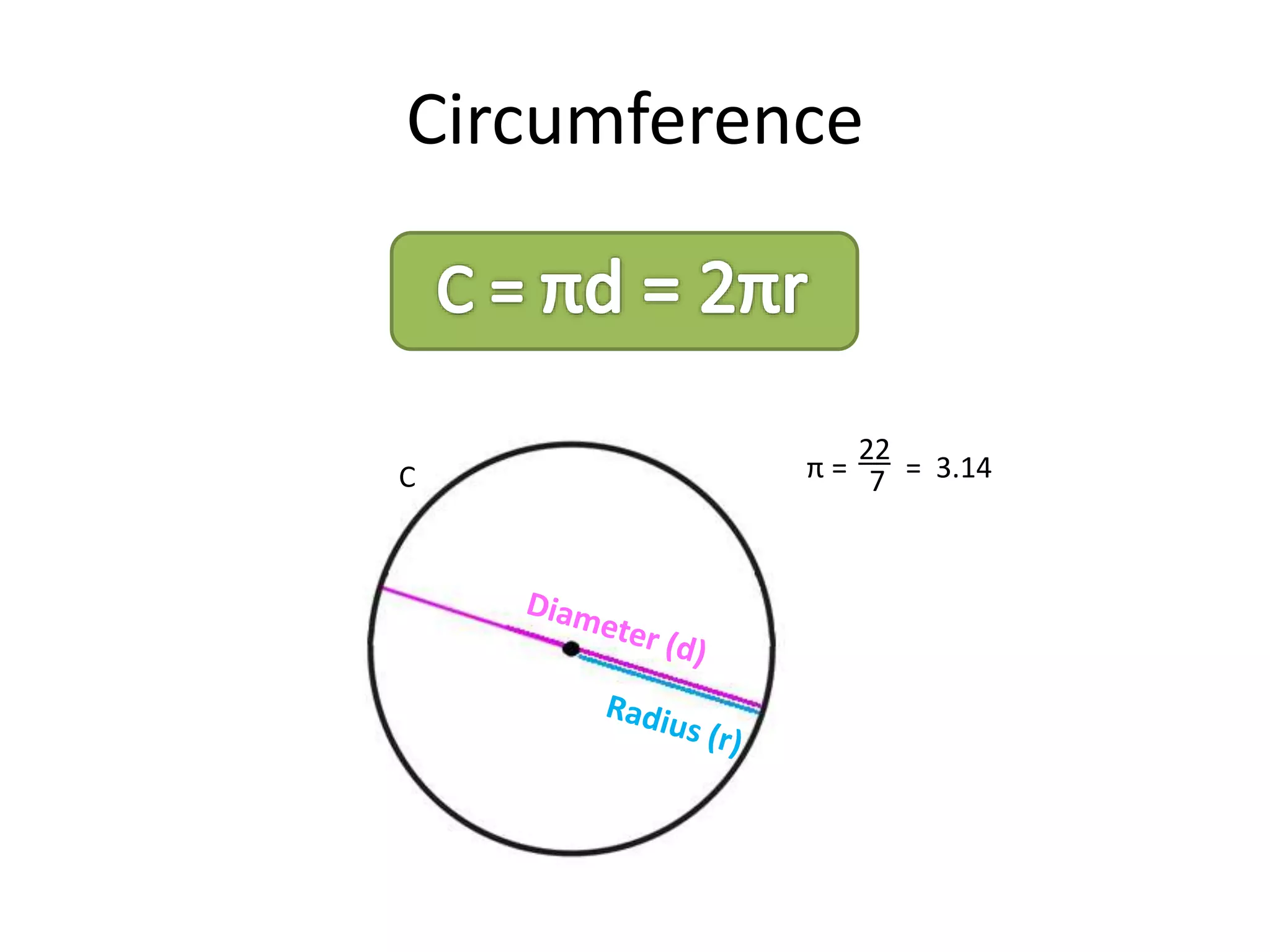
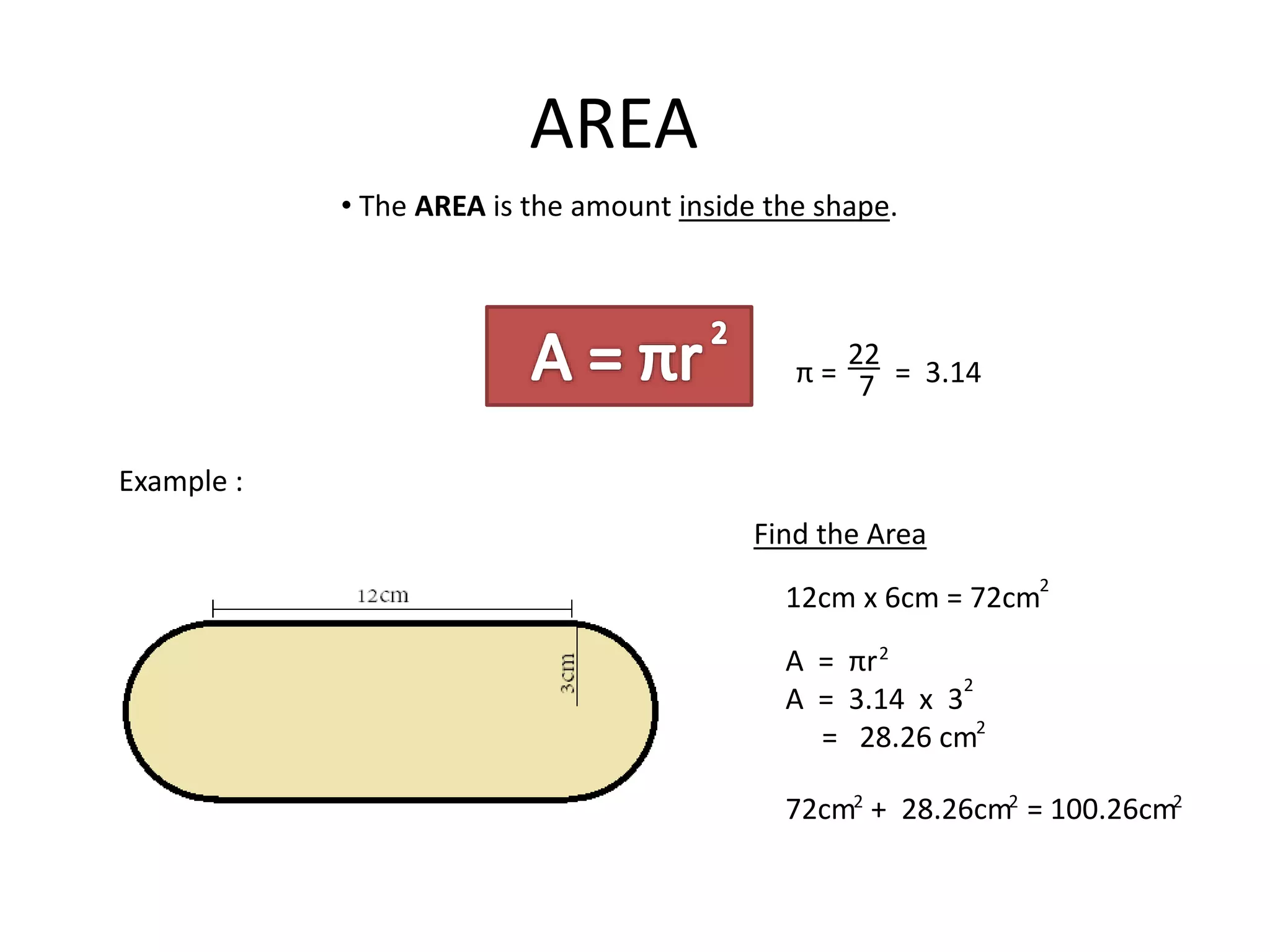
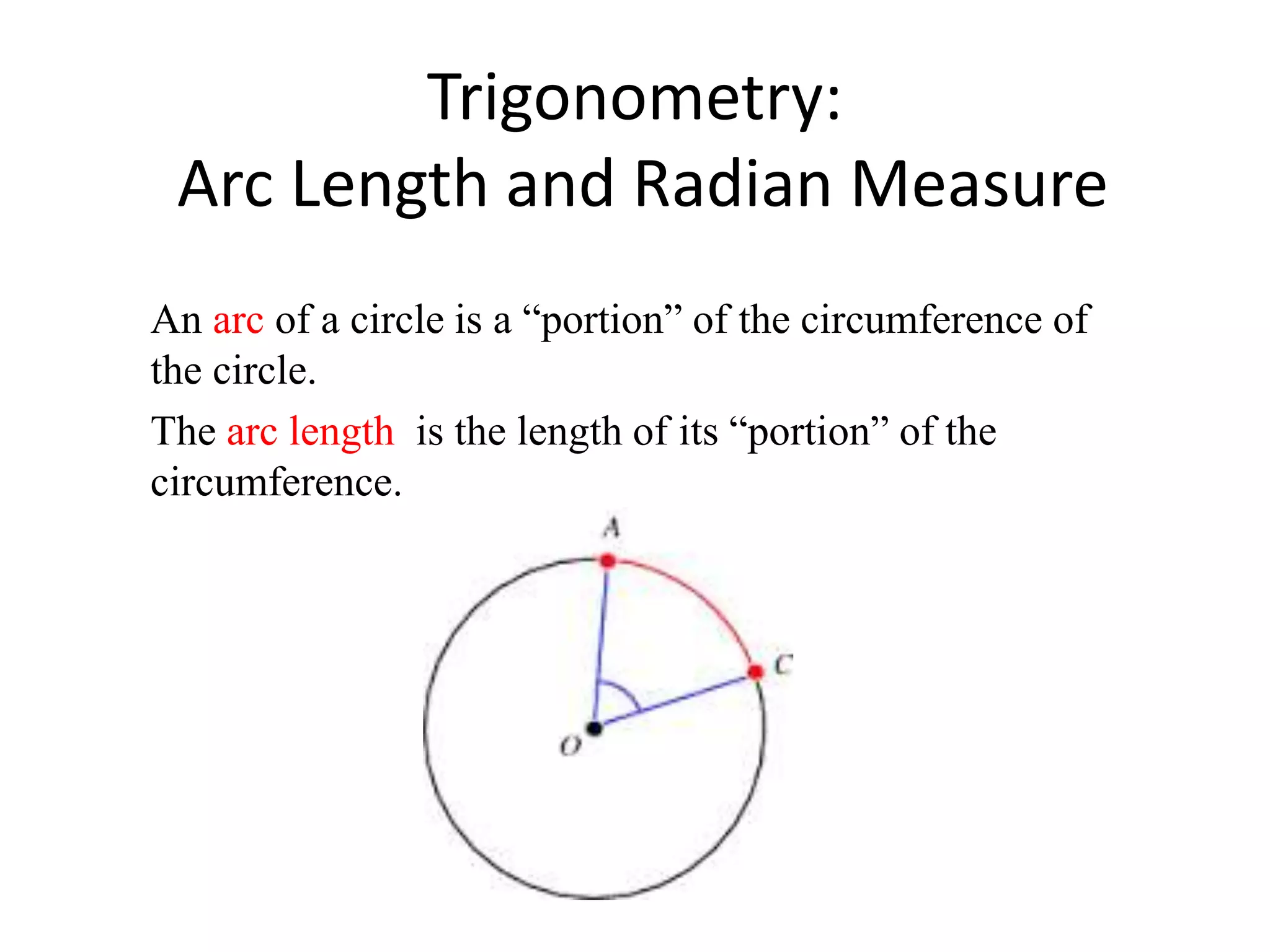
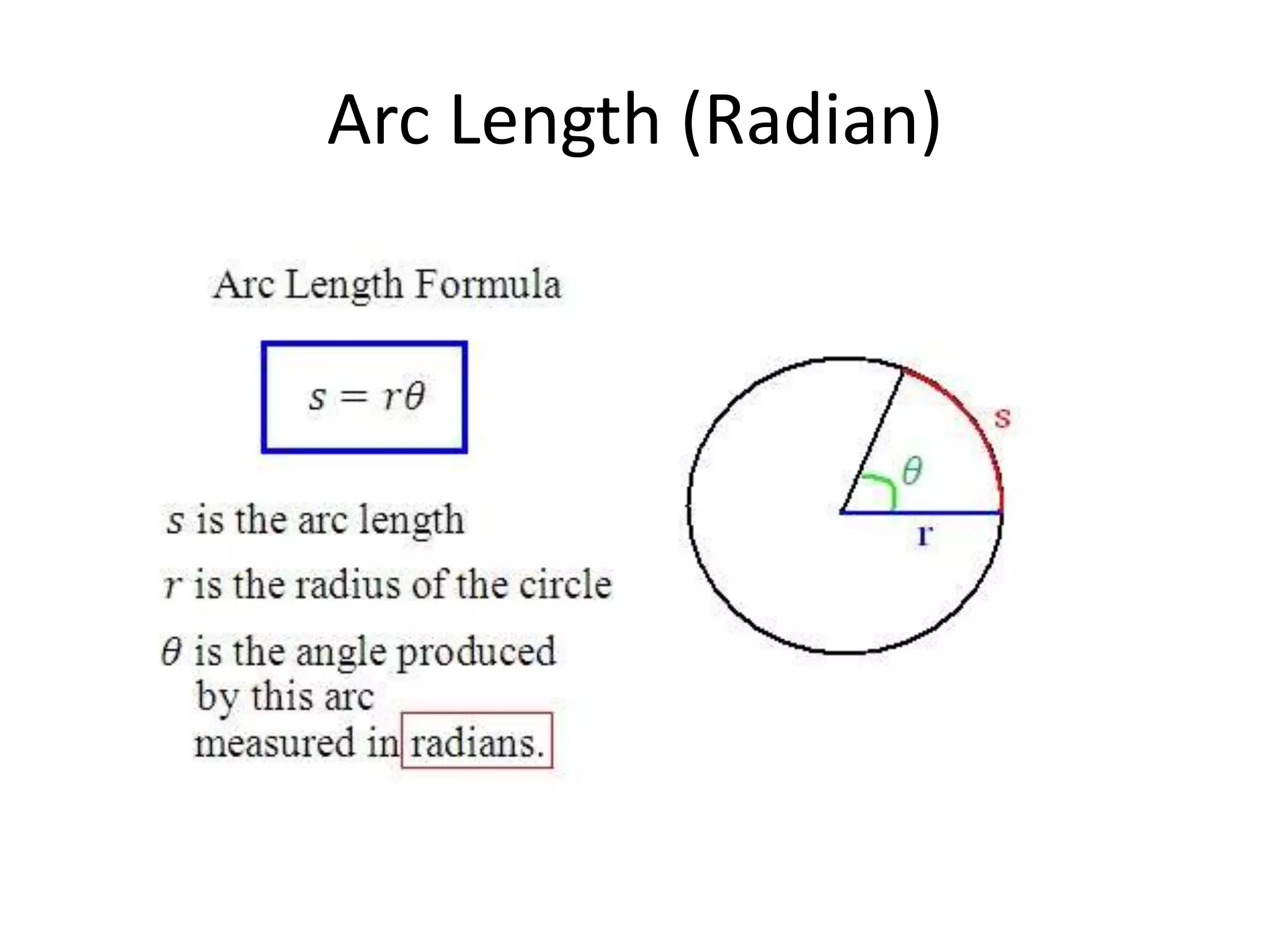
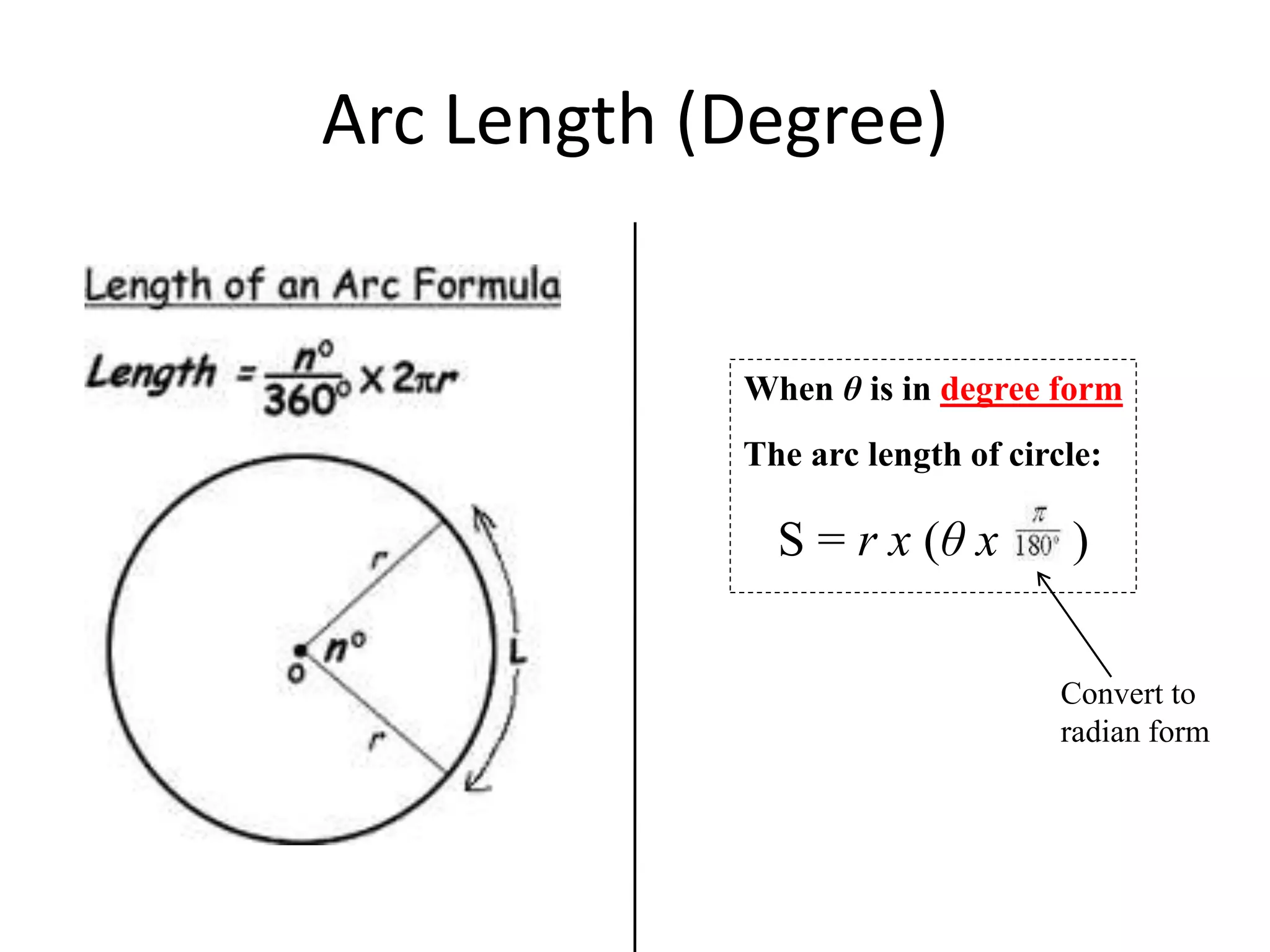
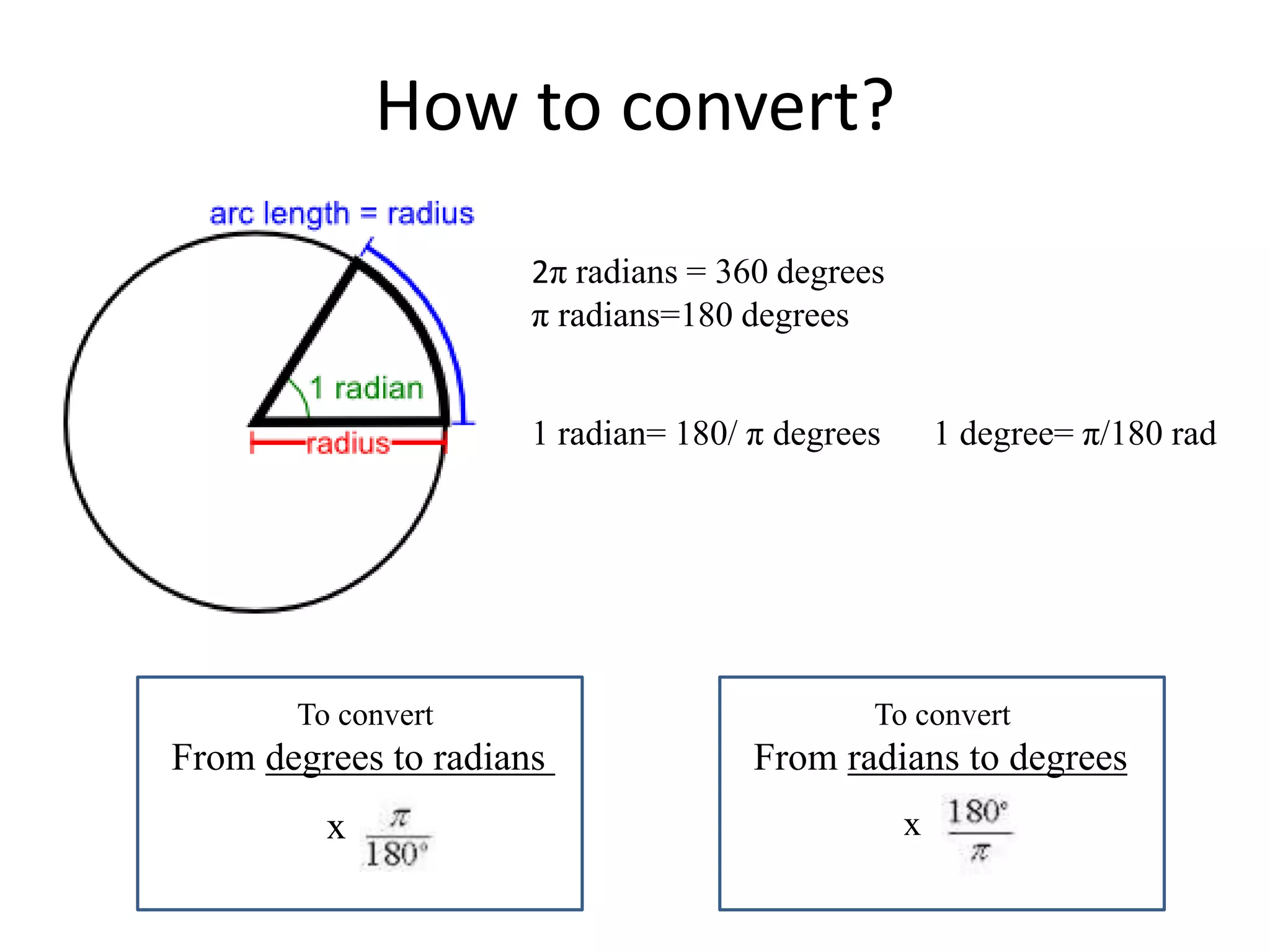
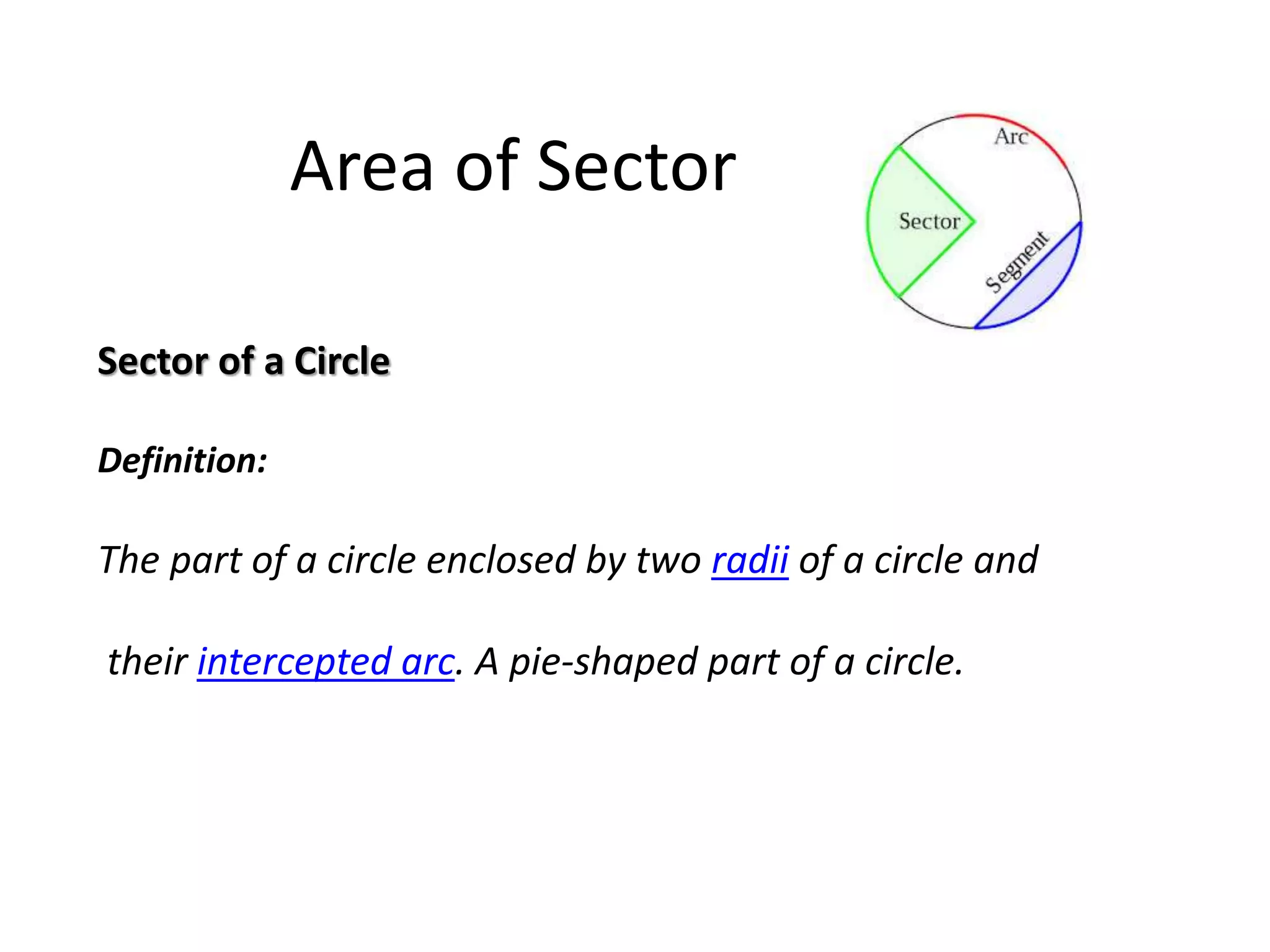
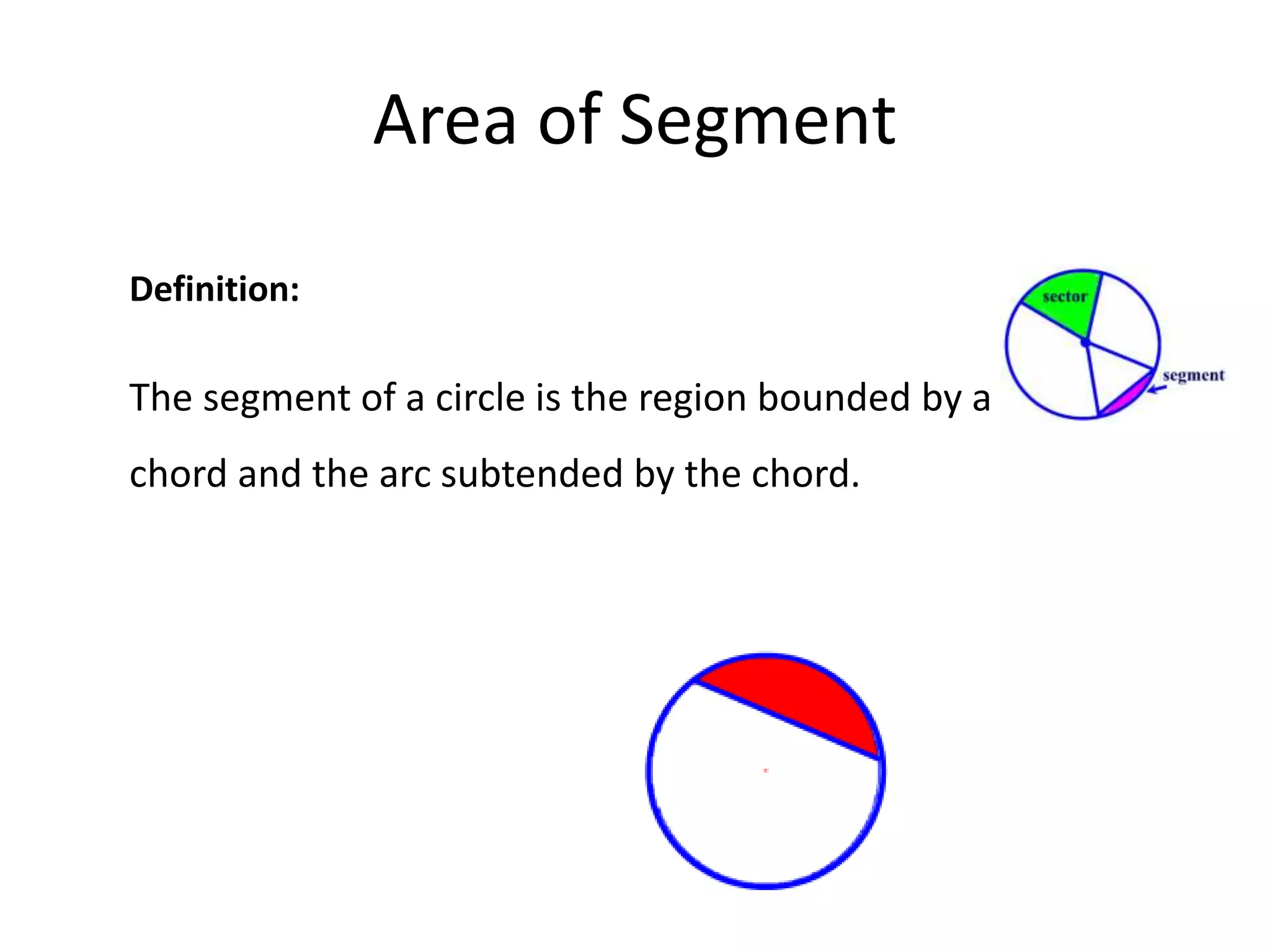
The document discusses geometric shapes related to circles such as spheres, hemispheres, and sectors. It provides formulas for calculating the surface area and volume of spheres and hemispheres. Formulas are given for finding the circumference, area, and radii of circles. The document also discusses converting between degrees and radians and formulas for calculating arc length, area of sectors, and area of segments of circles.

1. Circles and sphere

2. Sphere & Hemisphere
sphere
• A 3-dimensional object
shaped like a ball.
• Every point on the surface
is the same distance from
the center.
Hemisphere
• half of a sphere

3. Surface area of spheres
surface area = 4 π r2
• Example 1
If 'r' = 5 for a given sphere, and π = 3.14, then
the surface area of the sphere is:
surface area = 4 π r2
= 4 × 3.14 × 52
= 314

4. Volume of spheres
Question 1: Calculate the volume of a sphere of
radius 13 cm ?
Solution:
Given,
r = 13 cm
Volume of a sphere
= (4/3)πr3
= (4/3) π (13 cm)3
= 9202.772 cm3
Volume = (4/3) × π × r3

5. Surface area of hemisphere
Total surface area of a hemisphere:
S = (2πr2) + (πr2)
S = 3πr2
Curve area
Circle
Question 1: Find the radius of a hemisphere
where the total surface area is 1846.32 cm
Solution:The total surface area of the
hemisphere = 1846.32 cm2
We know, total surface area of a hemisphere
= 3 π r2 square units.

6. Answer
Therefore,
3 π r2 = 1846.32
3 ( 3.14 ) r2 =1846.32
9.42 r2 = 1846.32
r2 = 1814.929.42
r2 = 192.67
Radius of the hemisphere, r = 14 cm

7. Volume of hemisphere
• Volume of a hemisphere:
V = (1/2)(4/3)πr3
= (2/3)πr3
• Example: Calculate the volume of the hemisphere
with a radius of 3cm.
Answer:
Volume of Hemisphere: = (2/3)πr³
= 56.55 cm

8. SECTOR
CIRCLES
• The circle is the shape with the largest area for a given length of perimeter.
• A circle is a plane figure bounded by one line, and such that all right lines
drawn from a certain point within it to the bounding line, are equal.
• The Bounding line is called circumference.
c
Center
Center

9. Circumference
C π = = 3.14
22
7

10. AREA
π = = 3.14
22
7
• The AREA is the amount inside the shape.
Example :
Find the Area
A = πr
A = 3.14 x 3
= 28.26 cm
2
2
2
12cm x 6cm = 72cm
2
72cm + 28.26cm = 100.26cm2 2 2

11. Trigonometry:
Arc Length and Radian Measure
An arc of a circle is a “portion” of the circumference of
the circle.
The arc length is the length of its “portion” of the
circumference.

12. Arc Length (Radian)

13. Arc Length (Degree)
When θ is in degree form
The arc length of circle:
S = r x (θ x )
Convert to
radian form

14. How to convert?
2π radians = 360 degrees
π radians=180 degrees
1 radian= 180/ π degrees 1 degree= π/180 rad
To convert
From degrees to radians
x
To convert
From radians to degrees
x

15. Area of Sector
Sector of a Circle
Definition:
The part of a circle enclosed by two radii of a circle and
their intercepted arc. A pie-shaped part of a circle.

16. Semi-circle
(half of circle = half of area)
Quarter-Circle
(1/4 of circle = 1/4 of area)
Any Sector
(fractional part of the area)
where n is the
angle of the
sector in
degree
Area of Sector
where θ is angle
of sector
in radian form

17. Area of Segment
Definition:
The segment of a circle is the region bounded by a
chord and the arc subtended by the chord.

18. Example:
Find the area of a segment of a circle with a
central angle of 120 degrees and a radius of
8 Express answer to nearest integer.

19. Solution:
Start by finding the area of the sector: