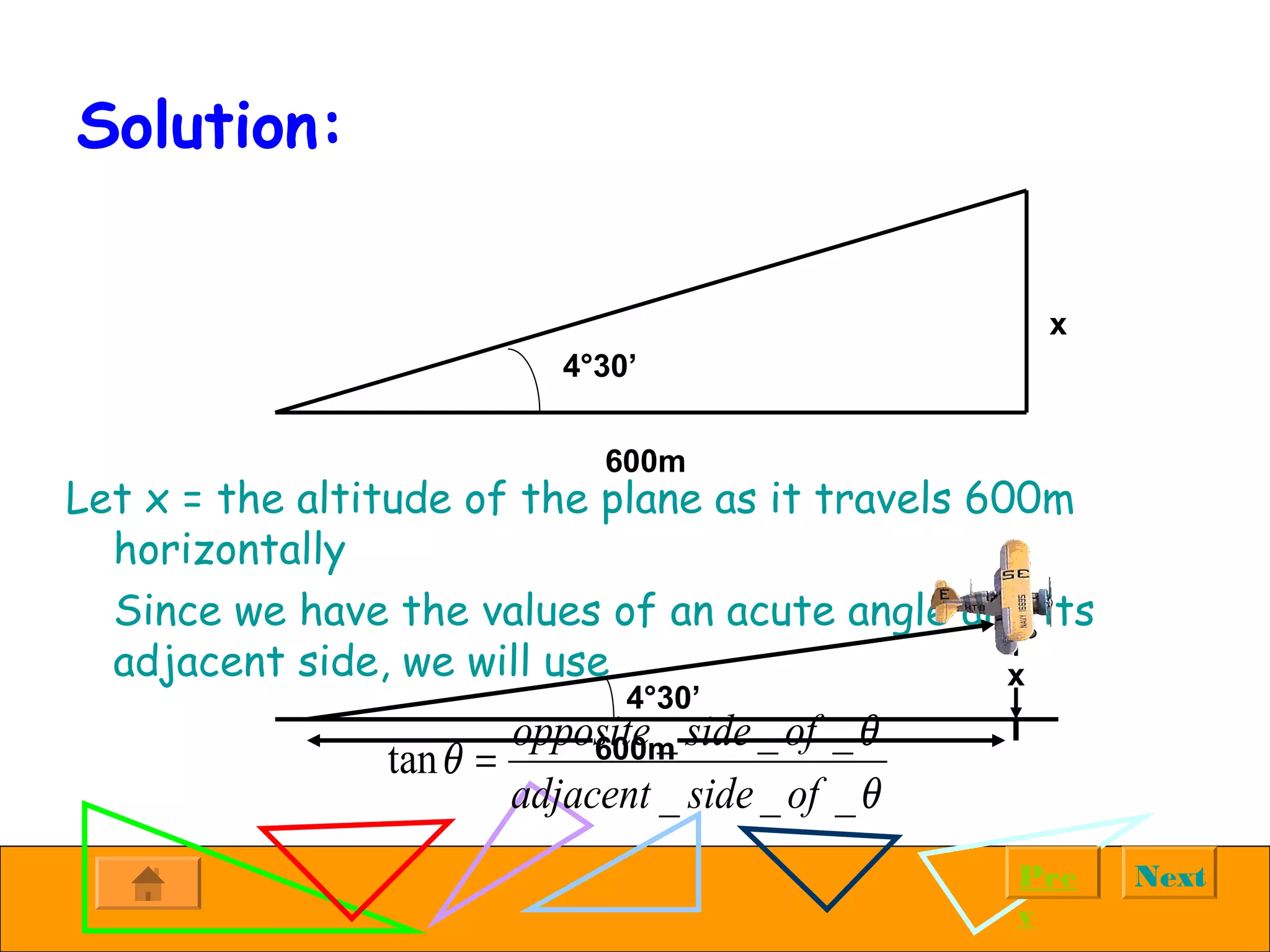
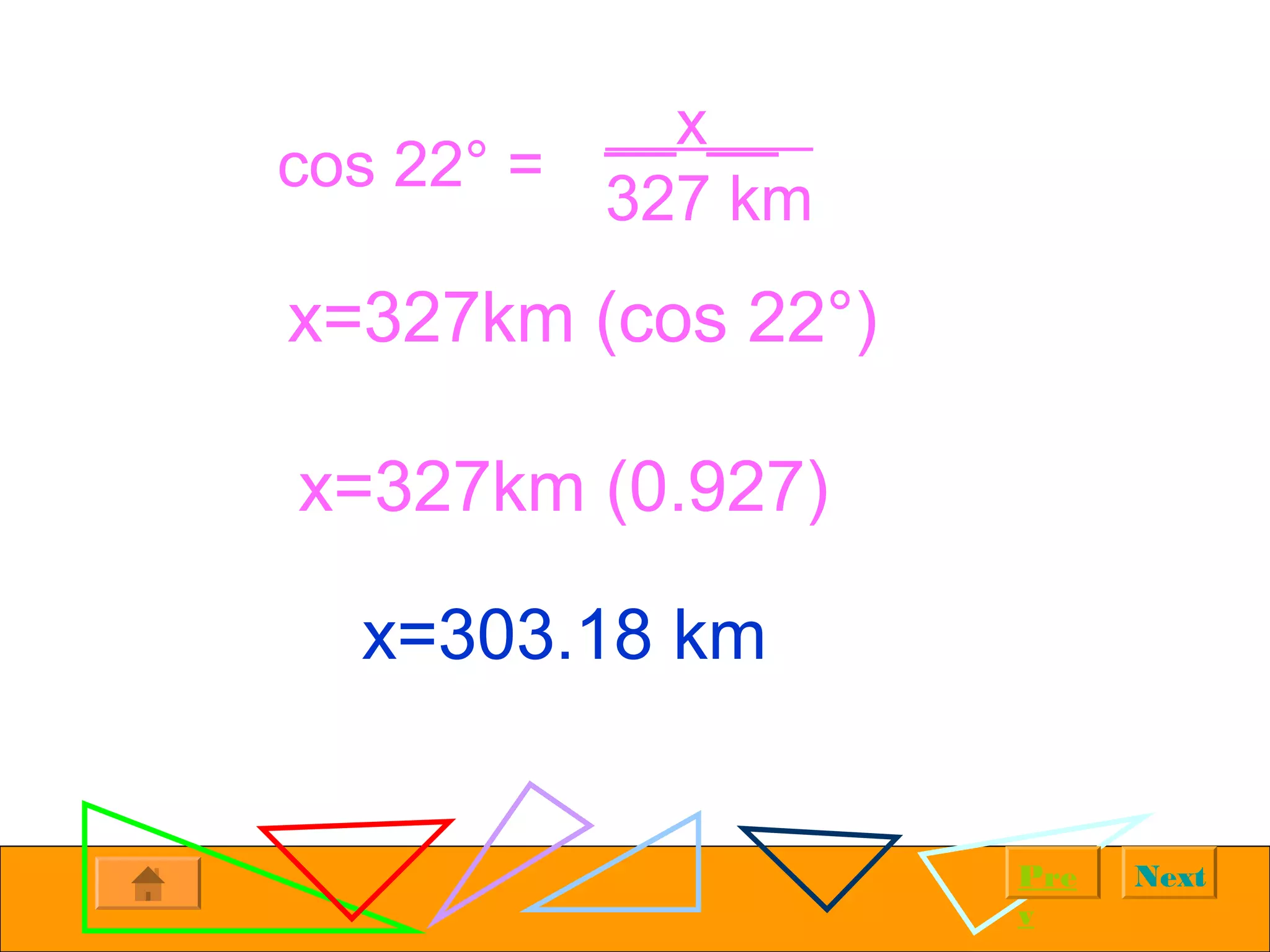
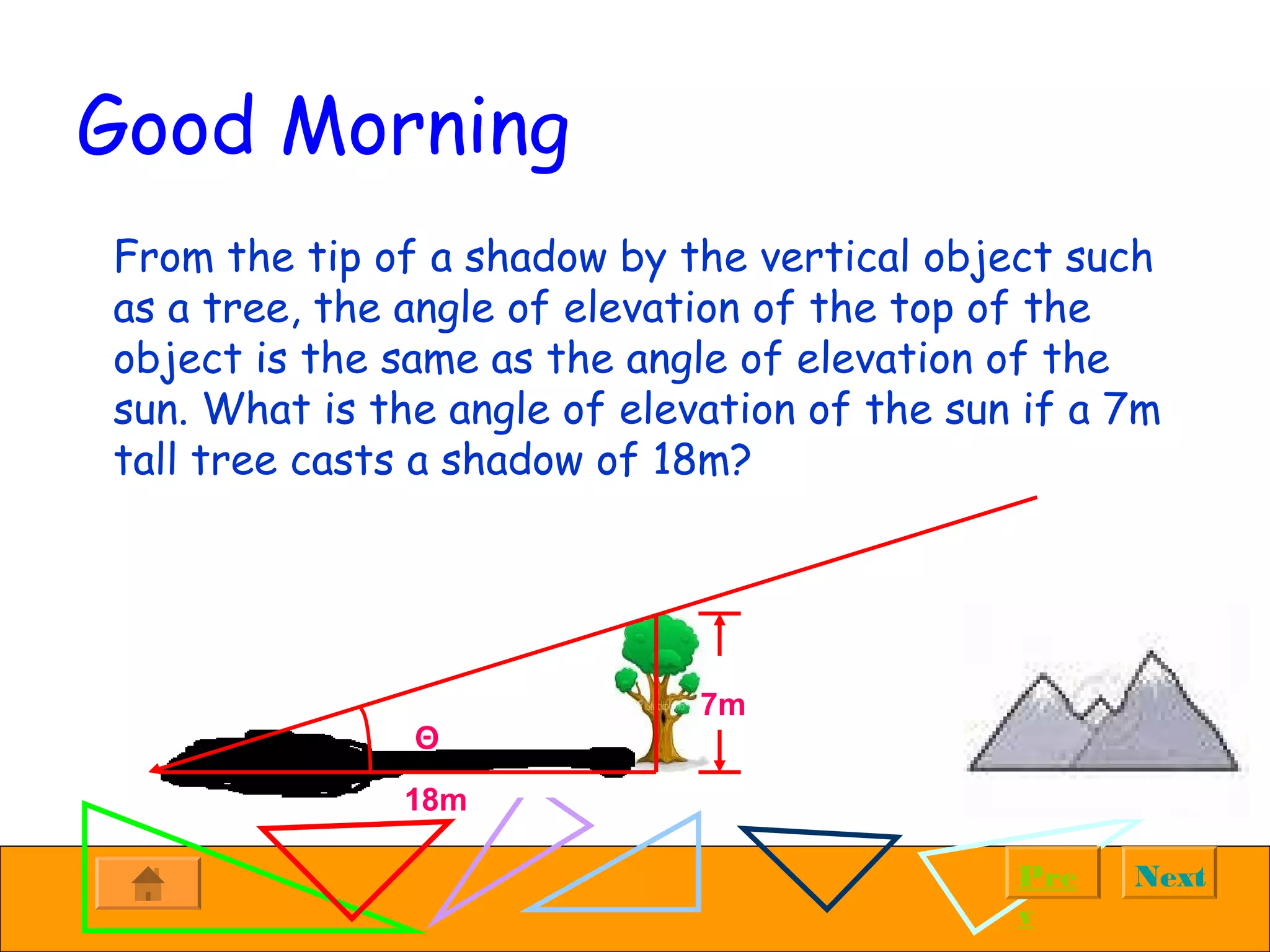
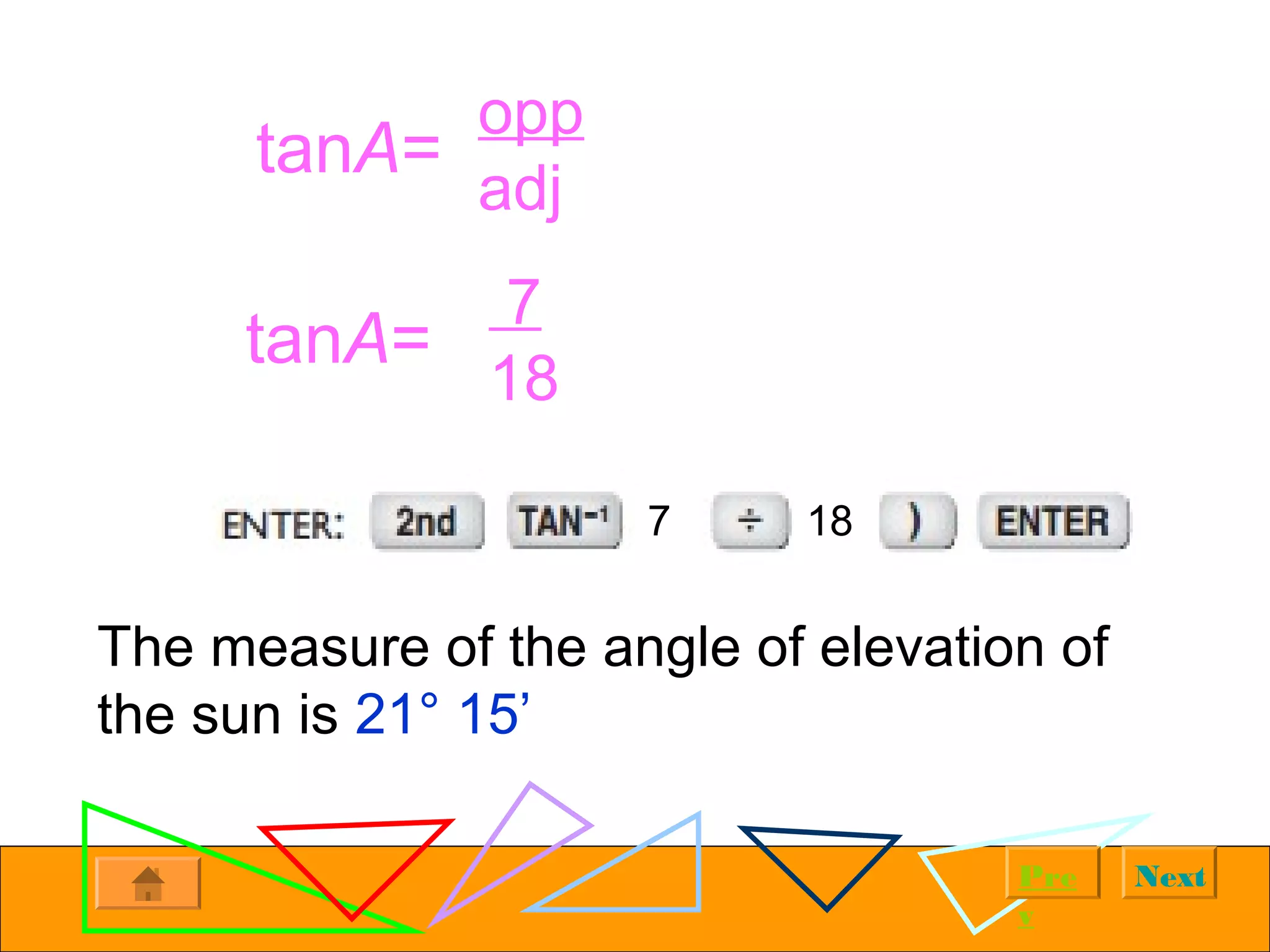
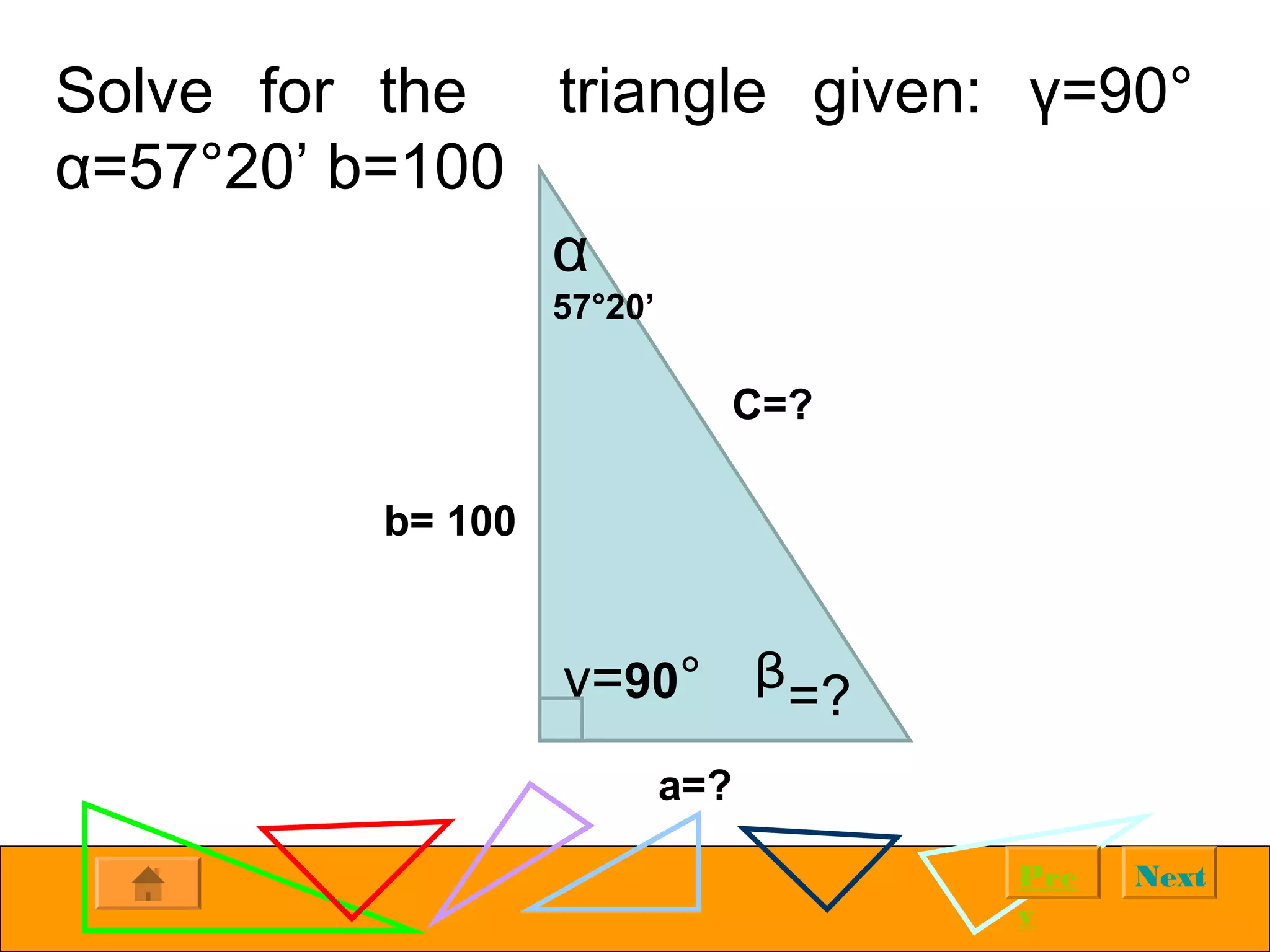
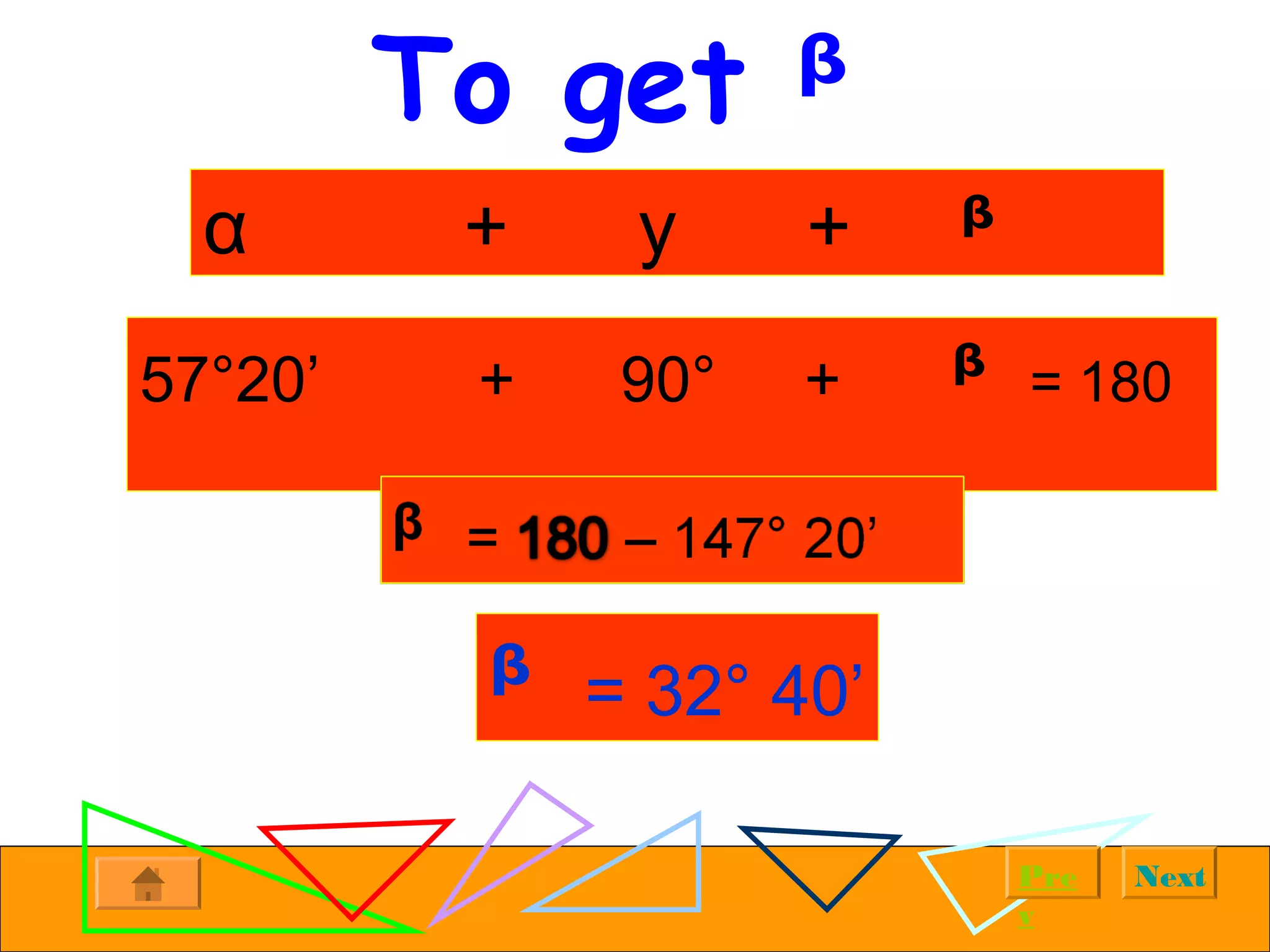
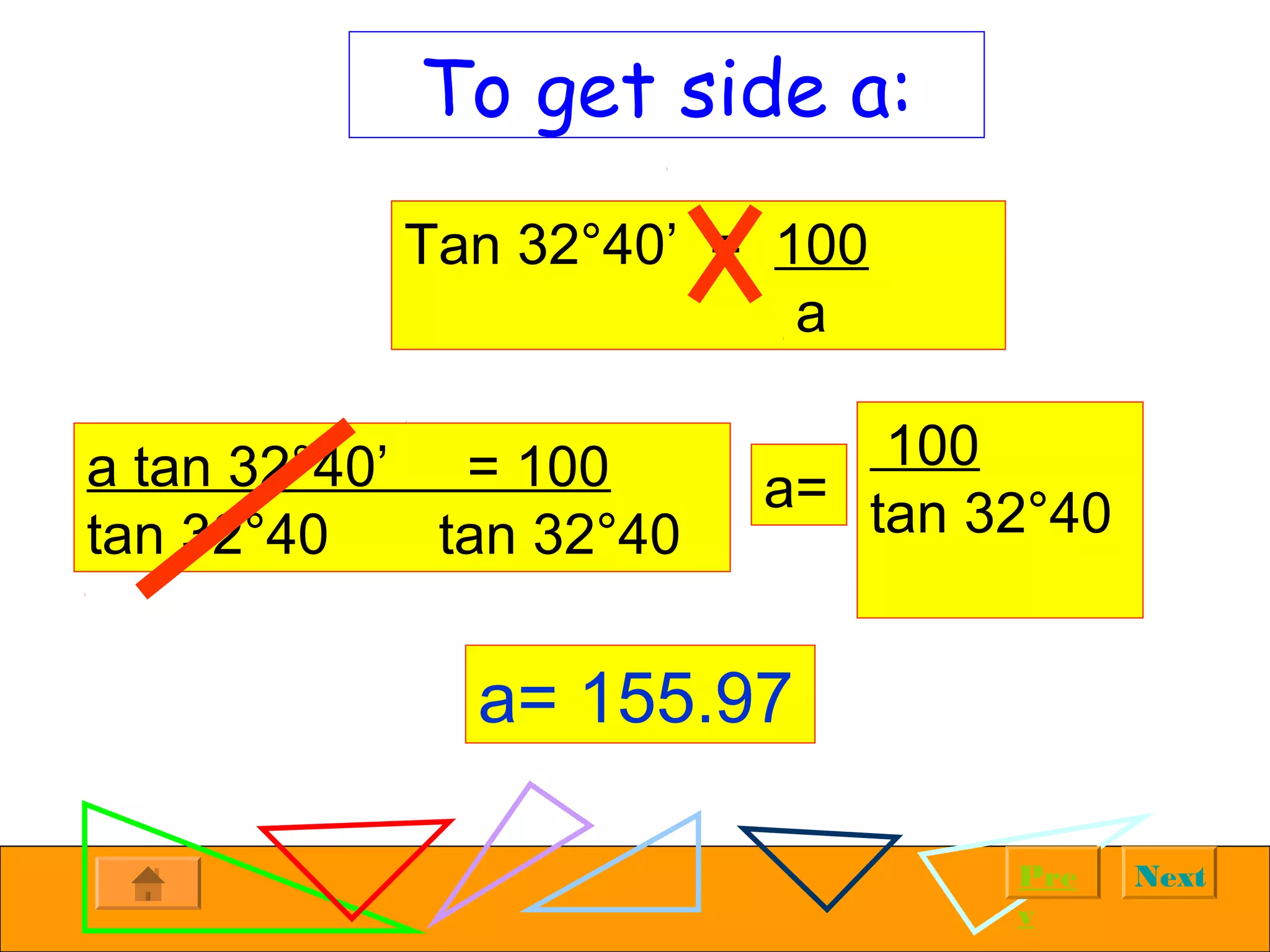
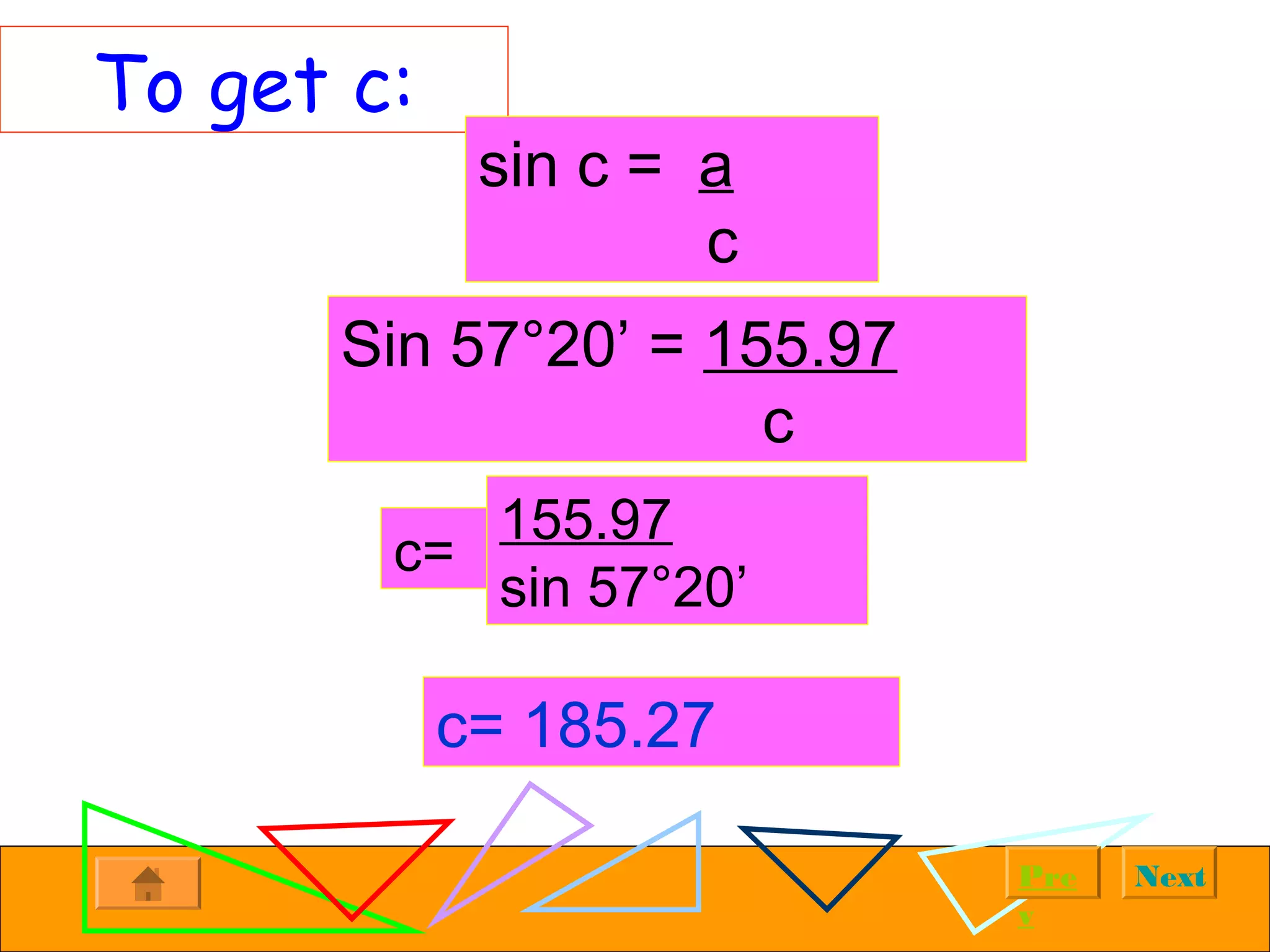
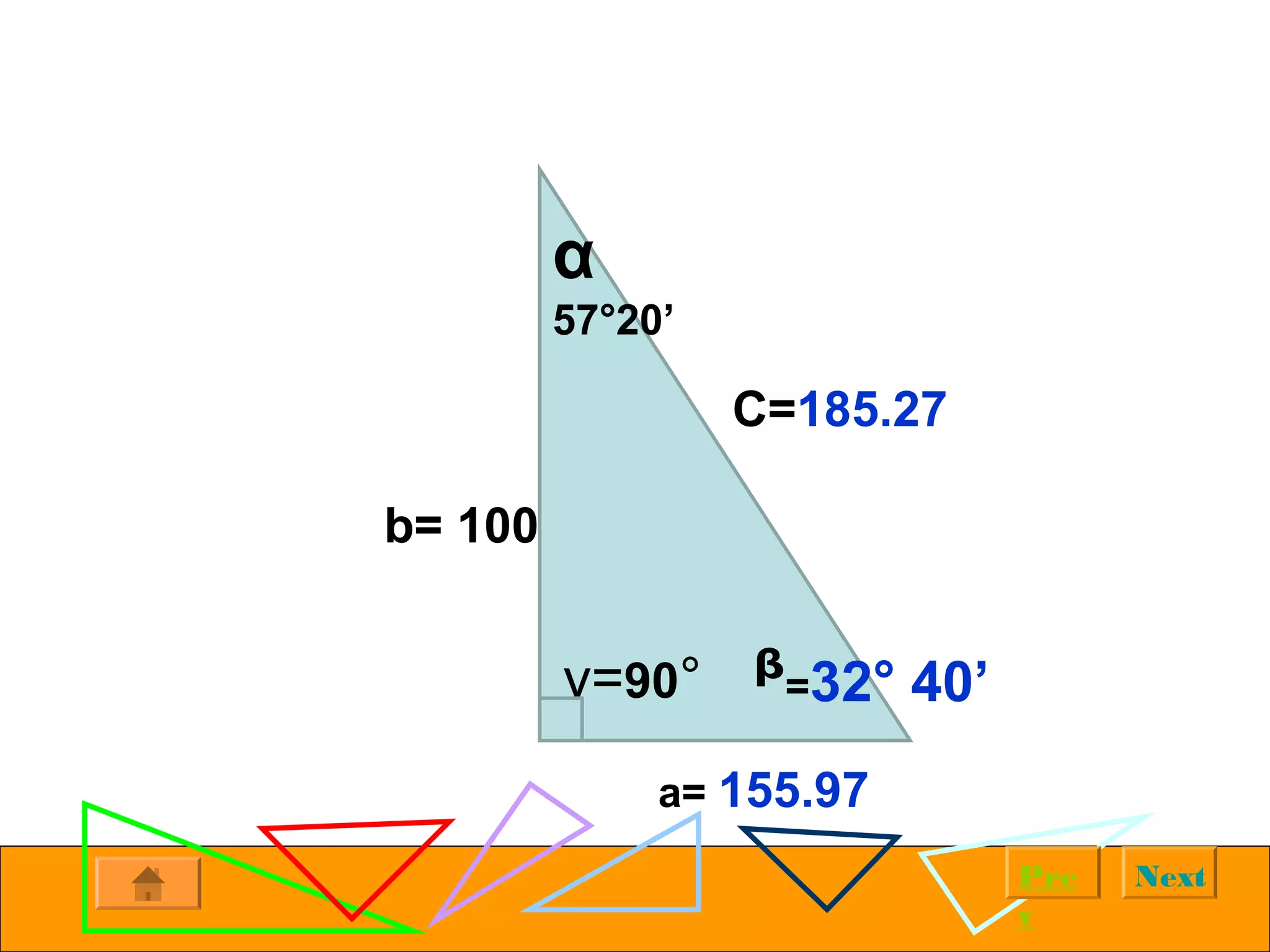
The document provides examples of solving right triangles using trigonometric functions. It first introduces right triangles and trigonometry. It then works through multiple examples, such as calculating the altitude of a plane given the horizontal distance traveled and angle of ascent. The examples demonstrate using trigonometric functions like tangent, cosine, and sine to solve for unknown sides and angles of right triangles based on given information.

1. NextPre
v

2. NextPre
v
Right Triangle in Real-Life
An Application to Right Triangle Trigonometry

3. NextPre
v
Introduction
• A triangle has three sides and three
angles. If three parts of a triangle, at
least one of which is side, are given then
other three parts can be uniquely
determined.
• Finding other unknown parts, when three
parts are known is called ‘solution of
triangle’.

4. NextPre
v
Example:
Fasten your seatbelts
A small plane takes off from an airport and rises
uniformly at an angle of 4°30’ with the horizontal
ground. After it has traveled over a horizontal
distance of 600m, what is the altitude of the plane to
the nearest meter?
x
600m
4°30’

5. NextPre
v
Solution:
Let x = the altitude of the plane as it travels 600m
horizontally
Since we have the values of an acute angle and its
adjacent side, we will use x
600m
4°30’
4°30’
600m
x
_ _ _
tan
_ _ _
opposite side of
adjacent side of
θ
θ
θ
=

6. NextPre
v
Let us solve
tan 4 30'
600
x
m
° =
600 (tan 4 30')
600 (0.0787)
47.22 47
x m
x m
x m m
= °
=
= :

7. NextPre
v
Let us solve
Answer:
The altitude of the plane after it has traveled
over a horizontal distance of 600m is 47m.
tan 4 30'
600
x
m
° =
600 (tan 4 30')
600 (0.0787)
47.22 47
x m
x m
x m m
= °
=
= :

8. NextPre
v
Let us solve some problems
Sail away
A ship sailed from a port with a bearing of S22°E.
How far south has the ship traveled after covering a
distance of 327km?
x
327km
22°

9. NextPre
v
__x__
327 km
x=327km (cos 22°)
x=327km (0.927)
x=303.18 km
cos 22° =

10. NextPre
v
Good Morning
From the tip of a shadow by the vertical object such
as a tree, the angle of elevation of the top of the
object is the same as the angle of elevation of the
sun. What is the angle of elevation of the sun if a 7m
tall tree casts a shadow of 18m?
Θ
7m
18m

11. NextPre
v
tanA=
opp
adj
tanA=
7
18
The measure of the angle of elevation of
the sun is 21° 15’
7 18

12. NextPre
v
Happy Landing
A plane is flying at an altitude of 1.5km. The pilot
wants to descend into an airport so that the path of
the plane makes an angle of 5° with the ground. How
far from the airport (horizontal distance) should the
descent begin?
1.5km
5°
x

13. NextPre
v
Solve for the other leg; call it "x"
EQUATION:
-----------
tan5°=
__x__
1.5 km
x= 1.5km
(tan 5°)
x= 1.5km (0.00878)
x= 17.1450 km

14. NextPre
v

15. NextPre
v
A ladder is placed 5 feet
from the foot of the wall. The
top of the ladder reaches a
point 12 feet above the
ground. Find the length of
the ladder

16. NextPre
v
Solution: The ladder, the wall and
the ground from a right triangle. The
length of the ladder is c, the length
of the hypotenuse of the right
triangle. The distance from the foot
of the ladder to the wall is a=5, and
the distance from the ground to the
top of the ladder is b= 12. Use the
Theorem of Pythagoras

17. NextPre
v

18. NextPre
v
Solve for the triangle given: γ=90°
α=57°20’ b=100
α
57°20’
y=90° ᵝ=?
b= 100
C=?
a=?

19. NextPre
v
To get ᵝ
57°20’ + 90° + ᵝ = 180
ᵝ = 32° 40’
α + y + ᵝ

20. NextPre
v
To get side a:
Tan 32°40’ = 100
a
a tan 32°40’ = 100
tan 32°40 tan 32°40
a=
a= 155.97
100
tan 32°40

21. NextPre
v
To get c:
sin c = a
c
Sin 57°20’ = 155.97
c
c=
155.97
sin 57°20’
c= 185.27

22. NextPre
v
α
57°20’
y=90° ᵝ=32° 40’
b= 100
C=185.27
a= 155.97

23. NextPre
v
Edgardo S. Mata
&
Ronaldo O. Abinal Jr.
Eng.Raymond Tandaan
Subj.Teacher