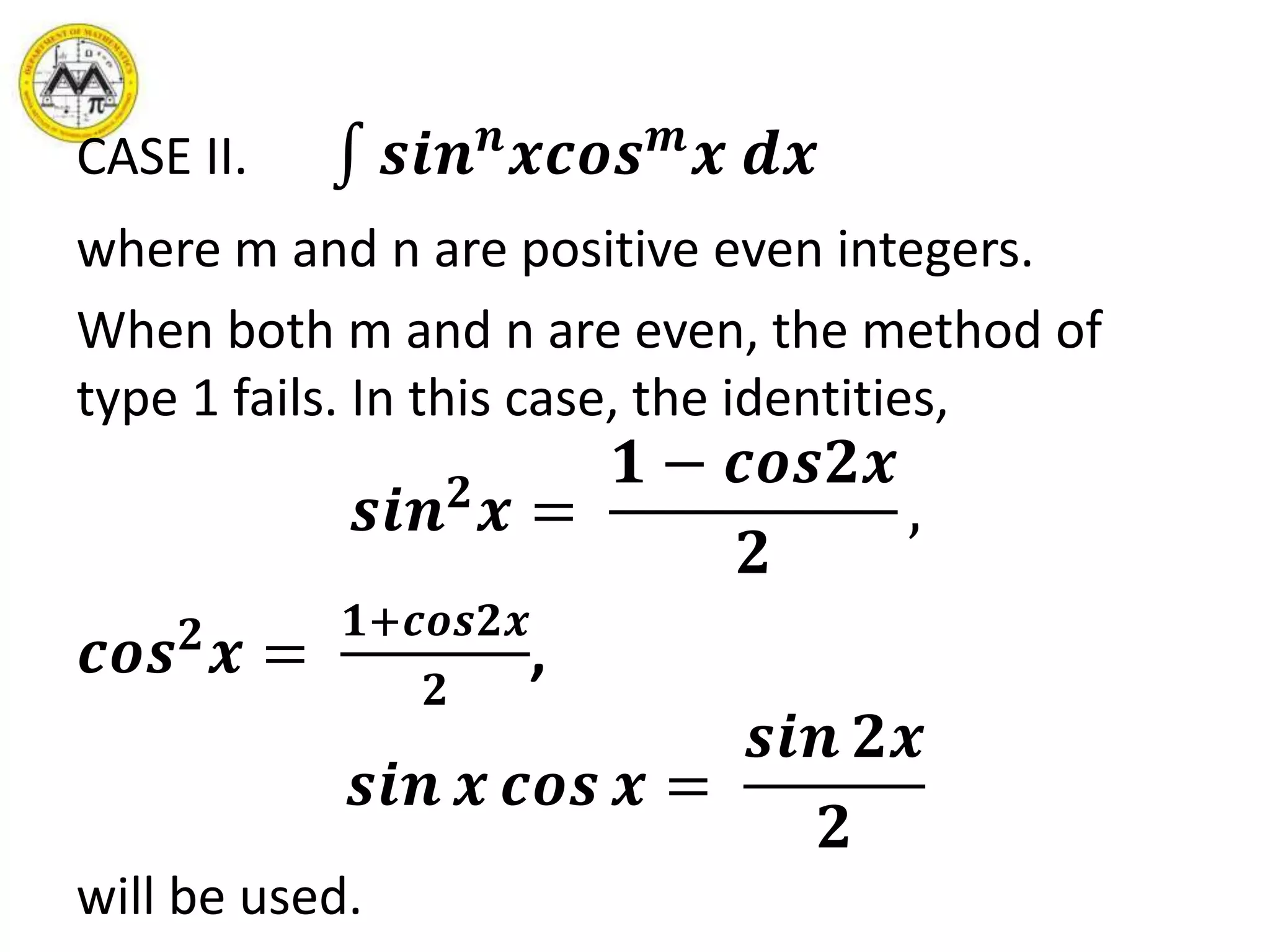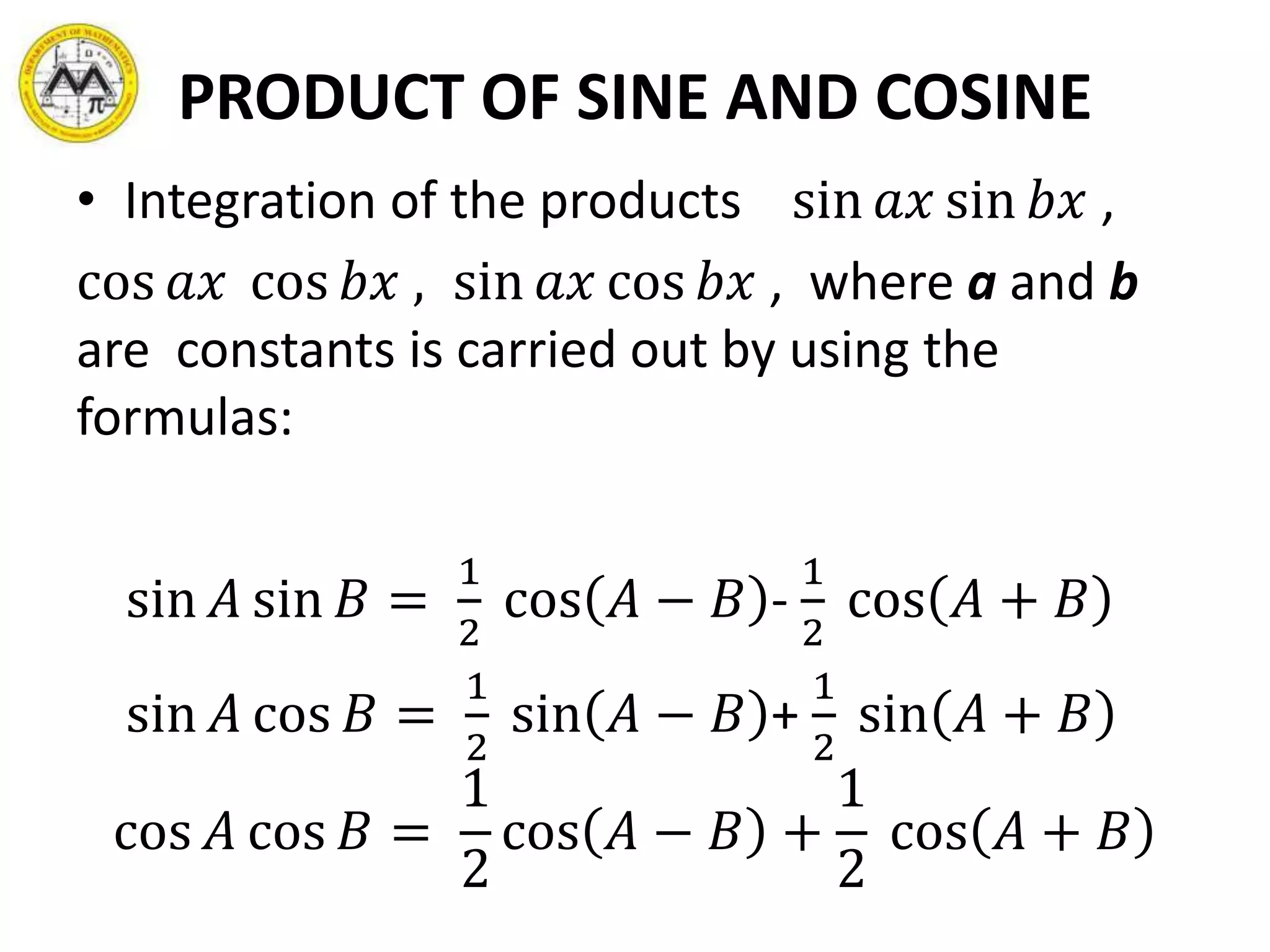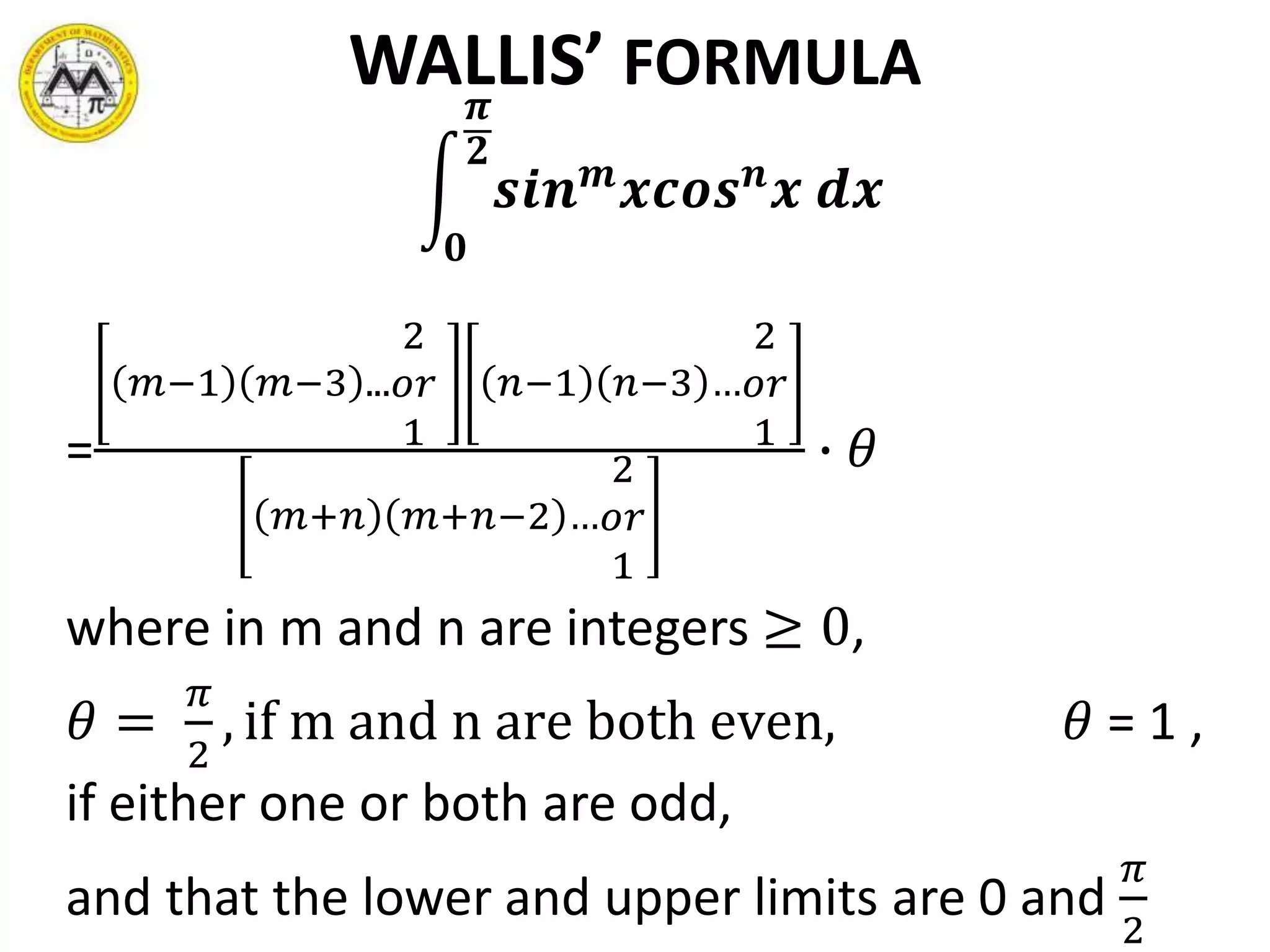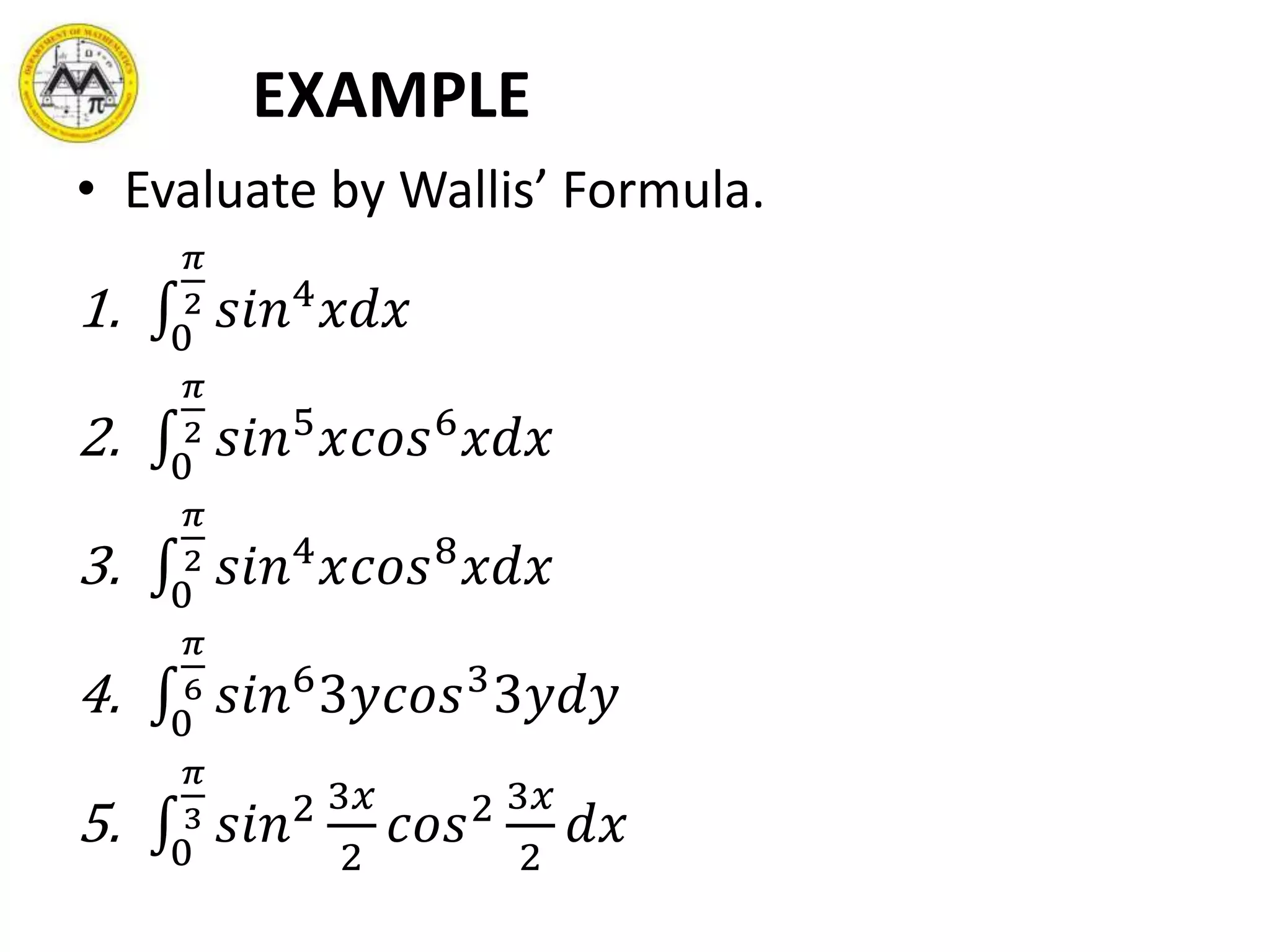Downloaded 110 times
Uploaded byLawrence De Vera
Lesson 9 transcendental functions
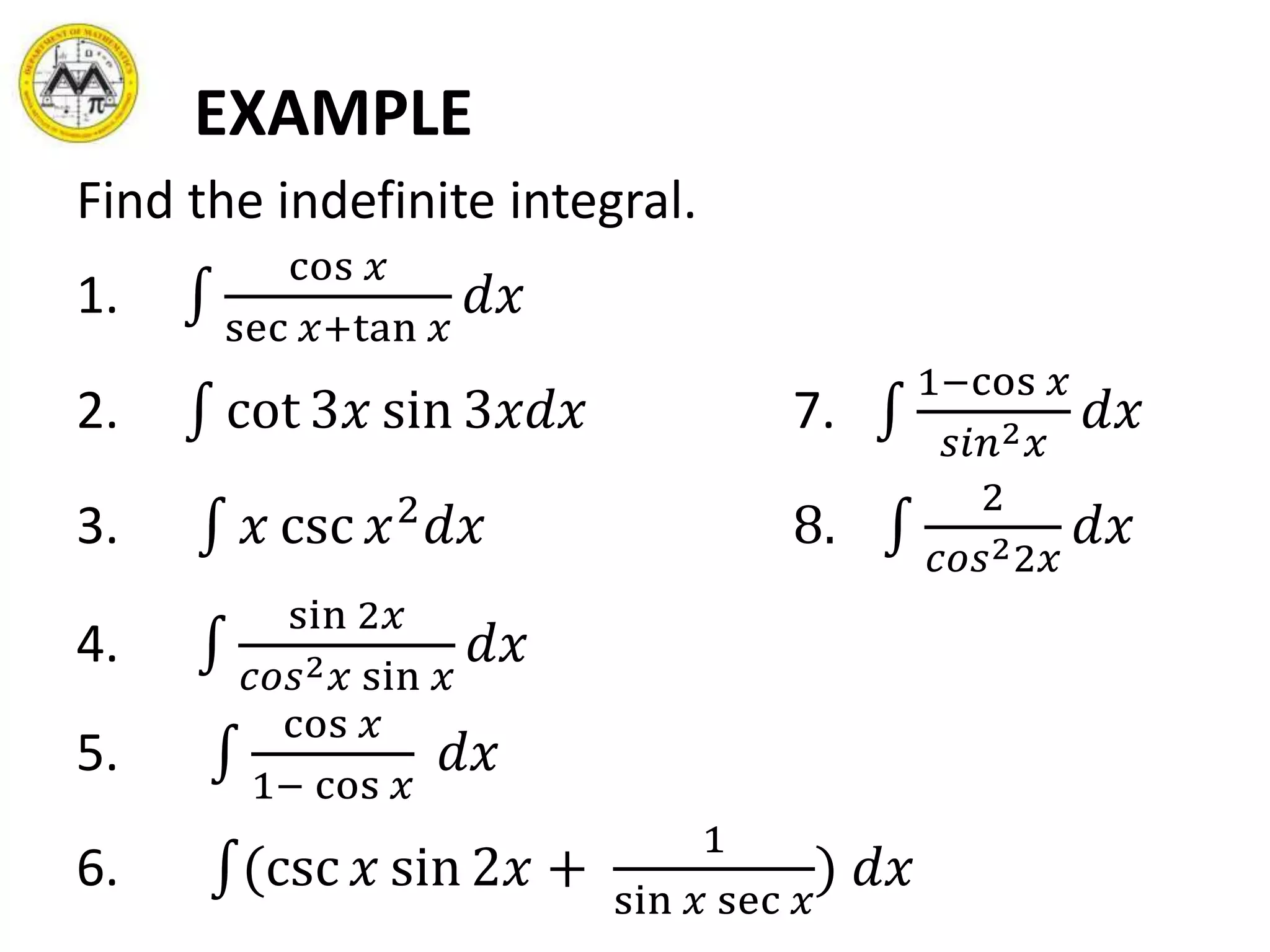
This document provides objectives and instructions for integrating various types of functions, including: - Rational functions using the Log Rule for Integration - Exponential functions - Trigonometric functions and their powers - Functions involving inverse trigonometric functions - Hyperbolic functions and inverse hyperbolic functions It also gives formulas and methods for integrating specific combinations of trigonometric, exponential, and other elementary functions.
More Related Content
Similar to Lesson 9 transcendental functions
Lesson 9 transcendental functions
- 1.
- 2. OBJECTIVES At the endof the lesson, the students are expected to: • use the Log Rule for Integration to integrate a rational functions. • integrate exponential functions. • integrate trigonometric functions. • integrate functions of the nth power of the different trigonometric functions. • use Walli’s Formula to shorten the solution in finding the antiderivative of powers of sine and cosine.
- 3. • integrate functionswhose antiderivatives involve inverse trigonometric functions. • use the method of completing the square to integrate a function. • review the basic integration rules involving elementary functions. • integrate hyperbolic functions. • integrate functions involving inverse hyperbolic functions.
- 4. LOG RULE FORINTEGRATION Let u be a differentiable function of x. 𝑑𝑢 𝑢 = 𝑙𝑛 𝑢 + 𝐶 or the above formula can also be written as 𝑢′ 𝑢 𝑑𝑥 = 𝑙𝑛 𝑢 + 𝐶 To apply this rule, look for quotients in which the numerator is the derivative of the denominator.
- 5. • EXAMPLE • Findthe indefinite integral. 1. 𝑥2 5−𝑥3 𝑑𝑥 5. 𝑠𝑒𝑐𝑥𝑡𝑎𝑛𝑥 𝑠𝑒𝑐𝑥−1 𝑑𝑥 2. 𝑥3−6𝑥−20 𝑥+5 𝑑𝑥 6. 𝑒2𝑥 𝑒 𝑥−1 𝑑𝑥 3. 1 𝑥𝑙𝑛𝑥3 𝑑𝑥 4. 1 𝑥 2 3 1+𝑥 1 3 𝑑𝑥
- 6. INTEGRATION OF EXPONENTIAL FUNCTIONS Letu be a differentiable function of x. 𝒆 𝒖 𝒅𝒖 = 𝒆 𝒖 + 𝒄 𝒂 𝒖 𝒅𝒖 = 𝒂 𝒖 𝒍𝒏𝒂 + c
- 7. EXAMPLE • Find theindefinite integral. 1. 𝑒 1 𝑥 𝑥2 𝑑𝑥 6. 𝑥473𝑥3 𝑑𝑥 2. 𝑒2𝑥 + 𝑒−𝑥 2 𝑑𝑥 3. 𝑥𝑒3𝑥2+4 𝑑𝑥 4. 5𝑒 𝑙𝑛𝑥2 𝑥 𝑑𝑥 5. 10 𝑥3 𝑥2 𝑑𝑥
- 8. BASIC TRIGONOMETRIC FUNCTIONS INTEGRATIONFORMULAS • cos 𝑢𝑑𝑢 = sin 𝑢 +c • sin 𝑢𝑑𝑢 = -cos 𝑢 + c • 𝑠𝑒𝑐2 𝑢𝑑𝑢 = tan 𝑢 + c • 𝑐𝑠𝑐2 𝑢𝑑𝑢 = -cot 𝑢 + 𝑐 • sec 𝑢 tan 𝑢𝑑𝑢 = sec 𝑢 + c • csc 𝑢 cot 𝑢 𝑑𝑢 = -csc 𝑢 + c • tan 𝑢𝑑𝑢 = ln sec 𝑢 + c or - lncos 𝑢 + c • cot 𝑢𝑑𝑢 = lnsin 𝑢 + c • sec 𝑢𝑑𝑢 = ln ( sec 𝑢 +tan 𝑢 ) + c • csc 𝑢𝑑𝑢 = -ln ( csc 𝑢 + cot 𝑢 ) + c
- 9. • In allthese formulas, u is an angle. In dealing with integrals involving trigonometric functions, transformations using the trigonometric identities are almost always necessary to reduce the integral to one or more of the standard forms.
- 10. EXAMPLE Find the indefiniteintegral. 1. cos 𝑥 sec 𝑥+tan 𝑥 𝑑𝑥 2. cot 3𝑥 sin 3𝑥𝑑𝑥 7. 1−cos 𝑥 𝑠𝑖𝑛2 𝑥 𝑑𝑥 3. 𝑥 csc 𝑥2 𝑑𝑥 8. 2 𝑐𝑜𝑠22𝑥 𝑑𝑥 4. sin 2𝑥 𝑐𝑜𝑠2 𝑥 sin 𝑥 𝑑𝑥 5. cos 𝑥 1− cos 𝑥 𝑑𝑥 6. (csc 𝑥 sin 2𝑥 + 1 sin 𝑥 sec 𝑥 ) 𝑑𝑥
- 11. TRANSFORMATION OF TRIGONOMETRIC FUNCTIONS Ifwe are given the product of an integral power of sin 𝑥 and an integral power of cos 𝑥, where in the powers may be equal or unequal, both even, both odd, or one is even the other odd, we use the trigonometric identities and express the given integrand as a power of a trigonometric function times the derivative of that function or as the sum of powers of a function times the derivative of the function • We shall now see how to perform the details under specified conditions.
- 12. POWERS OF SINEAND COSINE • CASE 1. 𝒔𝒊𝒏 𝒏 𝒖𝒄𝒐𝒔 𝒎 𝒖 𝒅𝒖 Transformations: a) If n is odd and m is even, 𝒔𝒊𝒏 𝒏 𝒖𝒄𝒐𝒔 𝒎 𝒖 = 𝒔𝒊𝒏 𝒏−𝟏 𝒖𝒄𝒐𝒔 𝒎 (𝒔𝒊𝒏 𝒖) b) If m isoddand n is even, 𝒔𝒊𝒏 𝒏 𝒖𝒄𝒐𝒔 𝒎 𝒖 = 𝒔𝒊𝒏 𝒏 𝒖𝒄𝒐𝒔 𝒎−𝟏 𝒖(𝒄𝒐𝒔𝒖) c) If n and m are both odd, transform the lesser power. If n and m are same degree either can be transformed
- 13. CASE II. 𝒔𝒊𝒏𝒏 𝒙𝒄𝒐𝒔 𝒎 𝒙 𝒅𝒙 where m and n are positive even integers. When both m and n are even, the method of type 1 fails. In this case, the identities, 𝒔𝒊𝒏 𝟐 𝒙 = 𝟏 − 𝒄𝒐𝒔𝟐𝒙 𝟐 , 𝒄𝒐𝒔 𝟐 𝒙 = 𝟏+𝒄𝒐𝒔𝟐𝒙 𝟐 , 𝒔𝒊𝒏 𝒙 𝒄𝒐𝒔 𝒙 = 𝒔𝒊𝒏 𝟐𝒙 𝟐 will be used.
- 14. EXAMPLE • Evaluate thefollowing integrals: 1. 𝑐𝑜𝑠3 𝑥𝑠𝑖𝑛7 𝑥 𝑑𝑥 2. 𝑠𝑖𝑛5 2𝑥𝑐𝑜𝑠5 2𝑥 𝑑𝑥 3 𝑠𝑖𝑛−3 𝑥𝑐𝑜𝑠5 𝑥 𝑑𝑥 4. 𝑠𝑖𝑛2 𝑥𝑐𝑜𝑠4 𝑥 𝑑𝑥 5. 𝑠𝑖𝑛4 2𝑥 𝑑𝑥 6. 𝑐𝑜𝑠2𝑥 + 2𝑠𝑖𝑛𝑥 2 𝑑𝑥 7. 𝑠𝑖𝑛6 𝑥𝑐𝑜𝑠4 𝑥 𝑑𝑥 8. 𝑠𝑖𝑛4 𝑥𝑐𝑜𝑠5 𝑥 𝑑𝑥 9. 0 𝜋 2 𝑠𝑖𝑛2 𝑥𝑐𝑜𝑠5 𝑥 𝑑𝑥 10. 0 𝜋 2 𝑠𝑖𝑛2 𝑥𝑐𝑜𝑠2 𝑥 𝑑𝑥
- 15. PRODUCT OF SINEAND COSINE • Integration of the products sin 𝑎𝑥 sin 𝑏𝑥 , cos 𝑎𝑥 cos 𝑏𝑥 , sin 𝑎𝑥 cos 𝑏𝑥 , where a and b are constants is carried out by using the formulas: sin 𝐴 sin 𝐵 = 1 2 cos 𝐴 − 𝐵 - 1 2 cos 𝐴 + 𝐵 sin 𝐴 cos 𝐵 = 1 2 sin 𝐴 − 𝐵 + 1 2 sin 𝐴 + 𝐵 cos 𝐴 cos 𝐵 = 1 2 cos 𝐴 − 𝐵 + 1 2 cos 𝐴 + 𝐵
- 16. EXAMPLE • Perform theindicated integrations: 1. cos 8𝑥 cos 5𝑥 𝑑𝑥 2. sin 6𝑥 cos 8𝑥 𝑑𝑥 3. 2 cos 6𝑥 cos −4𝑥 𝑑𝑥 4. 2 sin(2𝑥 − 𝜋) sin 3𝜋 − 2𝑥 𝑑𝑥 5. cos 5𝑥 cos 7𝑥 sin 3𝑥 𝑑𝑥 6. sin 4𝑥 sin 10𝑥 𝑑𝑥 7. 2 cos 2𝑥 cos 𝑥 𝑑𝑥 8. 3 sin 𝑥 cos 3𝑥 𝑑𝑥
- 17. WALLIS’ FORMULA 𝟎 𝝅 𝟐 𝒔𝒊𝒏 𝒎 𝒙𝒄𝒐𝒔𝒏 𝒙 𝒅𝒙 = 𝑚−1 𝑚−3 ... 2 𝑜𝑟 1 𝑛−1 𝑛−3 … 2 𝑜𝑟 1 𝑚+𝑛 𝑚+𝑛−2 … 2 𝑜𝑟 1 ∙ 𝜃 where in m and n are integers ≥ 0, 𝜃 = 𝜋 2 , if m and n are both even, 𝜃 = 1 , if either one or both are odd, and that the lower and upper limits are 0 and 𝜋 2
- 18. EXAMPLE • Evaluate byWallis’ Formula. 1. 0 𝜋 2 𝑠𝑖𝑛4 𝑥𝑑𝑥 2. 0 𝜋 2 𝑠𝑖𝑛5 𝑥𝑐𝑜𝑠6 𝑥𝑑𝑥 3. 0 𝜋 2 𝑠𝑖𝑛4 𝑥𝑐𝑜𝑠8 𝑥𝑑𝑥 4. 0 𝜋 6 𝑠𝑖𝑛6 3𝑦𝑐𝑜𝑠3 3𝑦𝑑𝑦 5. 0 𝜋 3 𝑠𝑖𝑛2 3𝑥 2 𝑐𝑜𝑠2 3𝑥 2 𝑑𝑥
- 19. POWERS OF TANGENTAND SECANT (COTANGENT AND COSECANT) I. 𝒕𝒂𝒏 𝒏 𝜽 𝒅𝜽 or 𝒄𝒐𝒕 𝒏 𝜽 𝒅𝜽 where n is a positive integer. When n=1 𝒕𝒂𝒏 𝒏 𝜽 𝒅𝜽= - ln𝒄𝒐𝒔 𝜽 + c 𝒄𝒐𝒕 𝒏 𝜽 𝒅𝜽 =ln sin 𝜽 + c When n≥ 1, we set 𝑡𝑎𝑛 𝑛 𝜃 equal to 𝑡𝑎𝑛 𝑛−2 𝜃 𝑡𝑎𝑛2 𝜃 𝑜𝑟 𝑐𝑜𝑡2 𝜃 𝑏𝑦 𝑐𝑜𝑡 𝑛−2 𝜃𝑐𝑜𝑡2 𝜃 , replace 𝑡𝑎𝑛2 𝜃 𝑏𝑦 𝑠𝑒𝑐2 𝜃 − 1 𝑜𝑟 𝑐𝑜𝑡2 𝜃 by (𝑐𝑠𝑐2 𝜃 − 1). Thus we get powers of tan𝜃 and by power formula, we can evaluate the integral.
- 20. II. 𝒔𝒆𝒄 𝒎 𝜽𝒕𝒂𝒏𝒏 𝜽 𝒅𝜽 𝒐𝒓 𝒄𝒔𝒄 𝒎 𝜽𝒄𝒐𝒕 𝒏 𝜽𝒅𝜽 where m and n are positive integers. • When m is even, we let 𝒔𝒆𝒄 𝒎 𝜽 = 𝒔𝒆𝒄 𝒎−𝟐 𝜽 𝒔𝒆𝒄 𝟐 𝜽, and express 𝒔𝒆𝒄 𝒎−𝟐 𝜽 = (𝒕𝒂𝒏 𝟐 𝜽 + 𝟏) 𝒎−𝟐 .We will then obtain products of powers of tan 𝜃 𝑏𝑦 𝑠𝑒𝑐2 𝜃. The integral could be integrated by means of power formula.
- 21. • If nis odd, we express 𝒔𝒆𝒄 𝒎 𝒕𝒂𝒏 𝒏 𝜽 = 𝒔𝒆𝒄 𝒎−𝟏 𝜽𝒕𝒂𝒏 𝒏−𝟏 𝜽(𝐬𝐞𝐜 𝜽 𝐭𝐚𝐧 𝜽).Then we transform 𝑡𝑎𝑛 𝑛−1 into power of sec𝜃 using the identity 𝒕𝒂𝒏 𝟐 𝜽 = 𝒔𝒆𝒄 𝟐 𝜽 − 𝟏. • If m is odd and n is even this can be evaluated using integration by parts
- 22. EXAMPLE • Find theindefinite integral. 1. 𝑡𝑎𝑛5 𝑥𝑑𝑥 2. 𝑡𝑎𝑛3 𝑥𝑠𝑒𝑐4 𝑥𝑑𝑥 3. 𝑐𝑠𝑐4 𝑥𝑑𝑥 4. 𝑐𝑜𝑡2 𝑥𝑐𝑠𝑐4 𝑥𝑑𝑥 5. 𝑡𝑎𝑛3 𝑥𝑠𝑒𝑐5 𝑥𝑑𝑥
- 23. INTEGRALS INVOLVING INVERSE TRIGONOMETRICFUNCTIONS • Let u be a differentiable function of x, and let a> 0. 1. 𝑑𝑢 𝑎2−𝑢2 = 𝑎𝑟𝑐𝑠𝑖𝑛 𝑢 𝑎 + 𝐶 2. 𝑑𝑢 𝑎2+𝑢2 = 1 𝑎 𝑎𝑟𝑐𝑡𝑎𝑛 𝑢 𝑎 + 𝐶 3. 𝑑𝑢 𝑢 𝑢2−𝑎2 = 1 𝑎 𝑎𝑟𝑐𝑠𝑒𝑐 𝑢 𝑎 + 𝐶
- 24. EXAMPLE • Find orevaluate the integral. 1. 𝑥−3 𝑥2+1 𝑑𝑥 6. 𝑙𝑛2 𝑙𝑛4 𝑒−𝑥 1−𝑒−2𝑥 𝑑𝑥 2. 𝑠𝑒𝑐2 𝑥 25−𝑡𝑎𝑛2 𝑥 𝑑𝑥 7. 𝑥 9+8𝑥2−𝑥4 𝑑𝑥 3. 3 2 𝑥(1+𝑥) 𝑑𝑥 8. 3 6 1 25+(𝑥−3)2 𝑑𝑥 4. 2 3 2𝑥−3 4𝑥−𝑥2 𝑑𝑥 9. 𝑥+2 −𝑥2−4𝑥 𝑑𝑥 5. −2 2 𝑑𝑥 𝑥2+4𝑥+13 10. 2𝑥−5 𝑥2+2𝑥+2 𝑑𝑥
- 25. HYPERBOLIC FUNCTIONS • Definitionsof the Hyperbolic Function 𝑠𝑖𝑛ℎ𝑥 = 𝑒𝑥 − 𝑒−𝑥 2 𝑐𝑠𝑐ℎ𝑥 = 1 𝑠𝑖𝑛ℎ𝑥 , 𝑥 ≠ 0 c𝑜𝑠ℎ𝑥 = 𝑒 𝑥+𝑒−𝑥 2 𝑠𝑒𝑐ℎ𝑥 = 1 𝑐𝑜𝑠ℎ𝑥 𝑡𝑎𝑛ℎ𝑥 = 𝑠𝑖𝑛ℎ𝑥 𝑐𝑜𝑠ℎ𝑥 𝑐𝑜𝑡ℎ𝑥 = 1 𝑡𝑎𝑛ℎ𝑥 , 𝑥 ≠ 0
- 26. • HYPERBOLIC IDENTITIES 𝑐𝑜𝑠ℎ2 𝑢− 𝑠𝑖𝑛ℎ2 𝑢 = 1 𝑡𝑎𝑛ℎ2 𝑢 + 𝑠𝑒𝑐ℎ2 𝑢 = 1 𝑐𝑜𝑡ℎ2 𝑢 − 𝑐𝑠𝑐ℎ2 𝑢 = 1 cosh2u = 𝑐𝑜𝑠ℎ2 𝑢 + 𝑠𝑖𝑛ℎ2 𝑢 𝑠𝑖𝑛ℎ2𝑥 = 2𝑠𝑖𝑛ℎ𝑥𝑐𝑜𝑠ℎ𝑥 𝑠𝑖𝑛ℎ2 1 2 𝑢 = 1 2 (𝑐𝑜𝑠ℎ 𝑢 − 1) 𝑐𝑜𝑠ℎ2 𝑥 = 1 + 𝑐𝑜𝑠ℎ2𝑥 2 tanh(x + y) = (𝑡𝑎𝑛ℎ 𝑥+𝑡𝑎𝑛ℎ 𝑦) 1+𝑡𝑎𝑛ℎ 𝑥 𝑡𝑎𝑛ℎ𝑦
- 27. INTEGRALS OF HYPERBOLICFUNCTIONS Let u be a differentiable function of x. 1. 𝑠𝑖𝑛ℎ𝑢 𝑑𝑢 = 𝑐𝑜𝑠ℎ𝑢 + 𝐶 2. 𝑐𝑜𝑠ℎ𝑢 𝑑𝑢 = 𝑠𝑖𝑛ℎ𝑢 + 𝐶 3. 𝑡𝑎𝑛ℎ𝑢 𝑑𝑢 = 𝑙𝑛 𝑐𝑜𝑠ℎ𝑢 + 𝐶 4. 𝑐𝑜𝑡ℎ𝑢 𝑑𝑢 = 𝑙𝑛 𝑠𝑖𝑛ℎ 𝑢 + 𝐶 5. 𝑠𝑒𝑐ℎ𝑢 𝑑𝑢 = 𝑡𝑎𝑛−1 𝑠𝑖𝑛 6. 𝑐𝑠𝑐ℎ𝑢 𝑑𝑢 = 𝑙𝑛(𝑐𝑜𝑡ℎ 𝑢 − 𝑐𝑠𝑐ℎ𝑢) + 𝐶 7. 𝑠𝑒𝑐ℎ2 𝑢 𝑑𝑢 = 𝑡𝑎𝑛ℎ𝑢 + 𝐶 8. 𝑐𝑠𝑐ℎ2 𝑢 𝑑𝑢 = − 𝑐𝑜𝑡ℎ 𝑢 + 𝐶 9. 𝑠𝑒𝑐ℎ𝑢 𝑡𝑎𝑛ℎ𝑢 𝑑𝑢 = −𝑠𝑒𝑐ℎ𝑢 + 𝐶 10. 𝑐𝑠𝑐ℎ 𝑢 𝑐𝑜𝑡ℎ𝑢 𝑑𝑢 = −𝑐𝑠𝑐ℎ𝑢 + 𝐶
- 28. INVERSE HYPERBOLIC FUNCTIONS •Function Domain • 𝑠𝑖𝑛ℎ−1 𝑥 = 𝑙𝑛(𝑥 + 𝑥2 + 1)(−∞, +∞) • 𝑐𝑜𝑠ℎ−1 𝑥 = 𝑙𝑛(𝑥 + 𝑥2 − 1) 1, ∞ • 𝑡𝑎𝑛ℎ−1 𝑥 = 1 2 𝑙𝑛 1+𝑥 1−𝑥 −1,1 • 𝑐𝑜𝑡ℎ−1 𝑥 = 1 2 𝑙𝑛 𝑥+1 𝑥−1 −∞, −1 U(1, ∞) • 𝑠𝑒𝑐ℎ−1 𝑥 = 𝑙𝑛 1+ 1−𝑥2 𝑥 (0,1 • 𝑐𝑠𝑐ℎ−1 𝑥 = 𝑙𝑛 1 𝑥 + 1+𝑥2 𝑥 −∞, 0 U(0, ∞)
- 29. INTEGRATION INVOLVING INVERSE HYPERBOLICFUNCTION • Let u be a differentiable function of x. • 𝑑𝑢 𝑢2±𝑎2 = 𝑙𝑛 𝑢 + 𝑢2 ± 𝑎2 + 𝐶 • 𝑑𝑢 𝑎2−𝑢2 = 1 2𝑎 𝑙𝑛 𝑎+𝑢 𝑎−𝑢 + 𝐶 • 𝑑𝑢 𝑢 𝑎2±𝑢2 = − 1 𝑎 𝑙𝑛 𝑎+ 𝑎2±𝑢2 𝑢 + 𝐶
- 30. EXAMPLE • Find theindefinite integral. 1. 1 3−9𝑥2 𝑑𝑥 2. 1 𝑥 1+𝑥 𝑑𝑥 3. 1 1−4𝑥−2𝑥2 𝑑𝑥 4. 𝑑𝑥 (𝑥+2) 𝑥2+4𝑥+8 5. 𝑥 1+𝑥3 𝑑𝑥