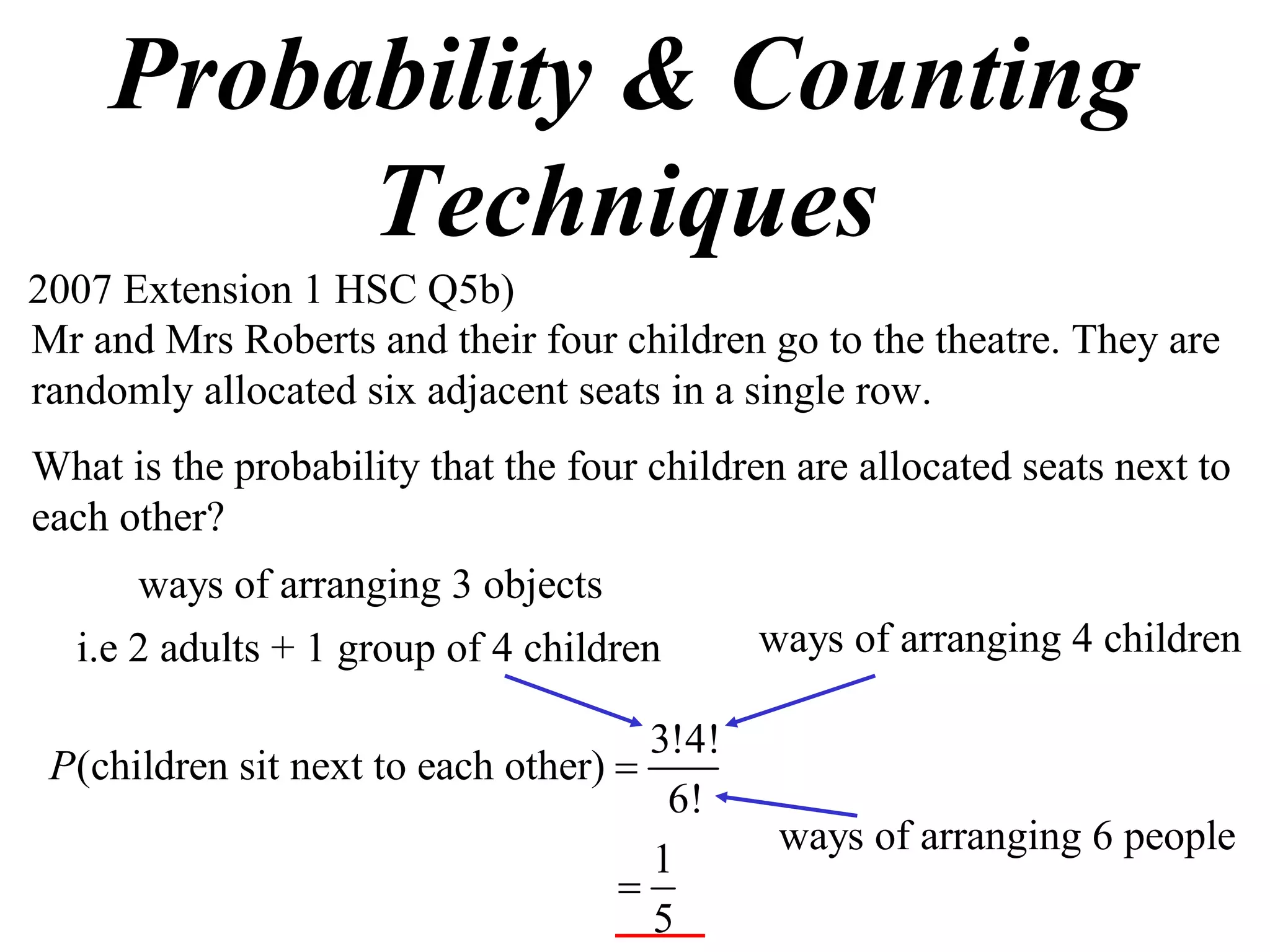
- A chess match between a Home and Away team is played across 4 boards
- The probability of the Home team winning, drawing, or losing on each board is given
- The results are recorded as a string of W, D, L indicating the outcome on each board
- There are 81 possible result recordings as there are 3 possible outcomes on each of the 4 boards
- The probability of the result "WDLD" is calculated as the product of the probabilities of each individual outcome