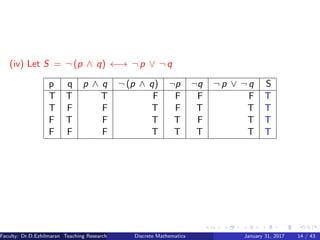
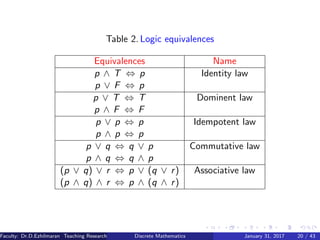
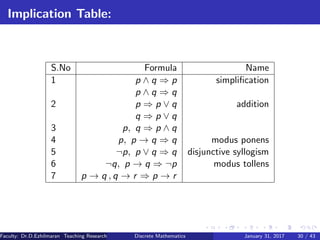
This document provides an overview of a course on discrete mathematics and graph theory taught by Dr. D. Ezhilmaran and M. Adhiyaman at VIT University in Tamil Nadu, India. It covers topics like mathematical logic, statement calculus, propositional logic, truth tables, logical equivalence, inference rules, and validity of arguments. Definitions, examples, and truth tables are provided to explain concepts like atomic statements, connectives, tautologies, and logical implications between statements. The document is intended as an introduction to the key concepts and techniques involved in propositional logic and reasoning.