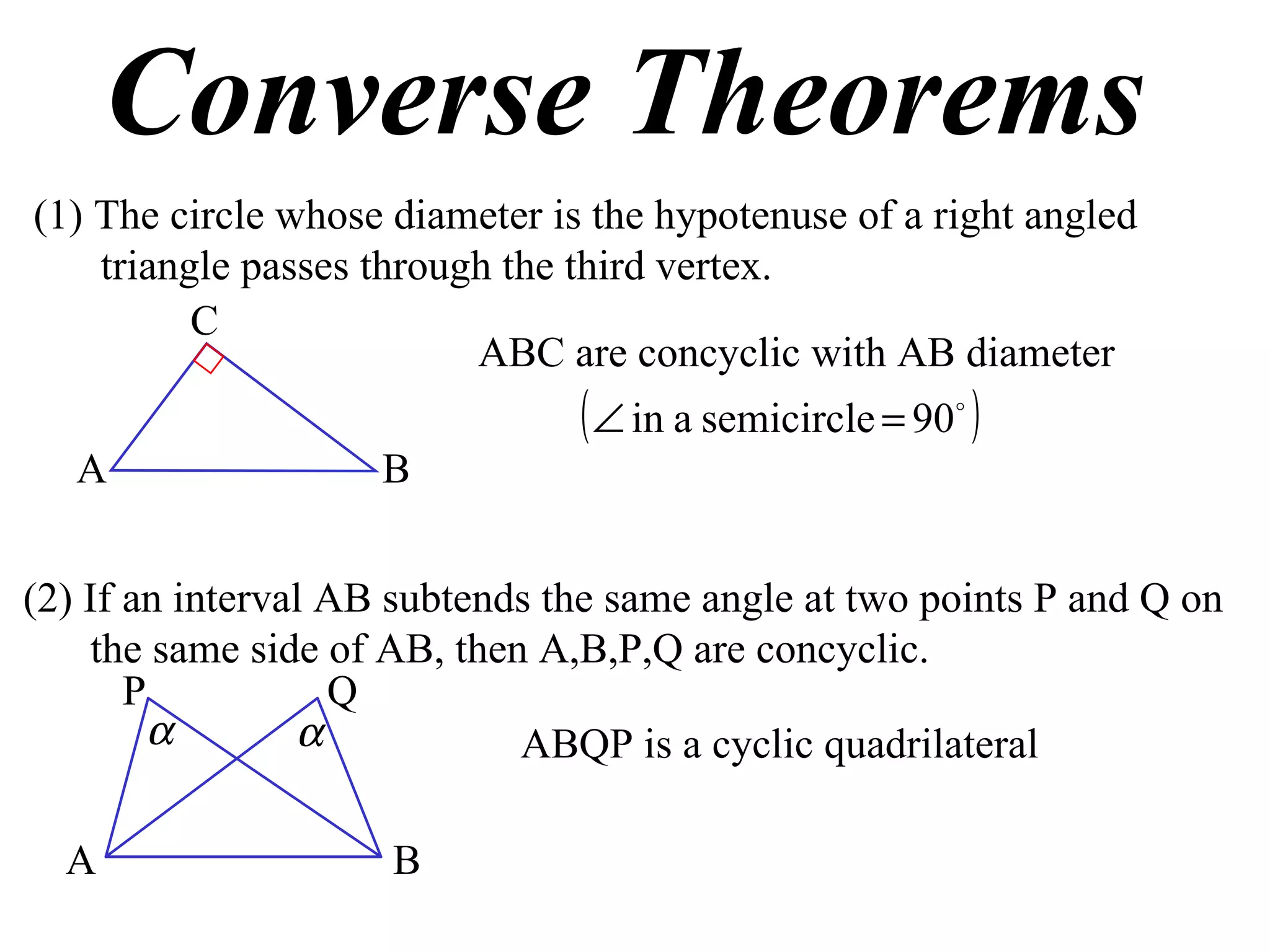
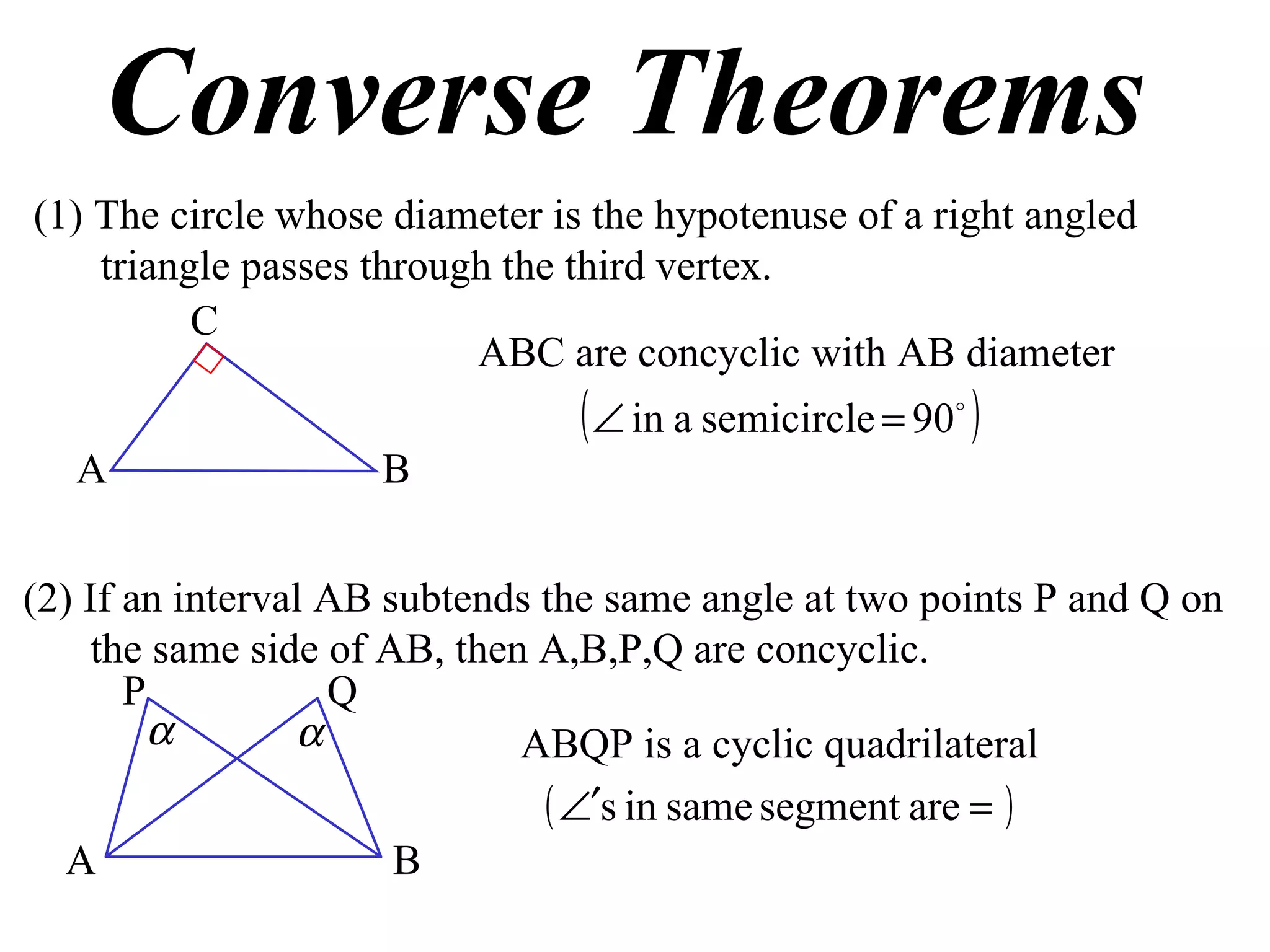
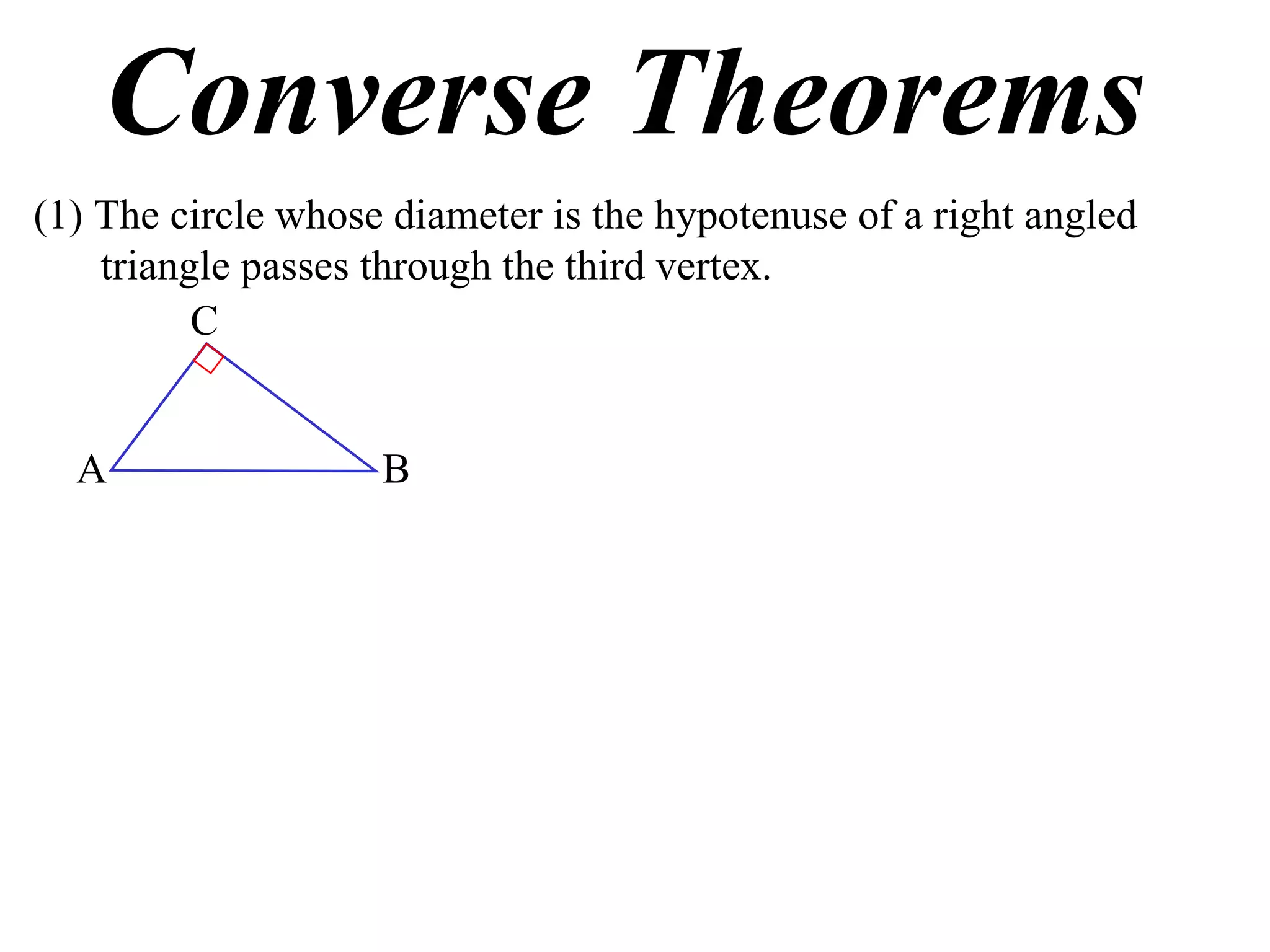
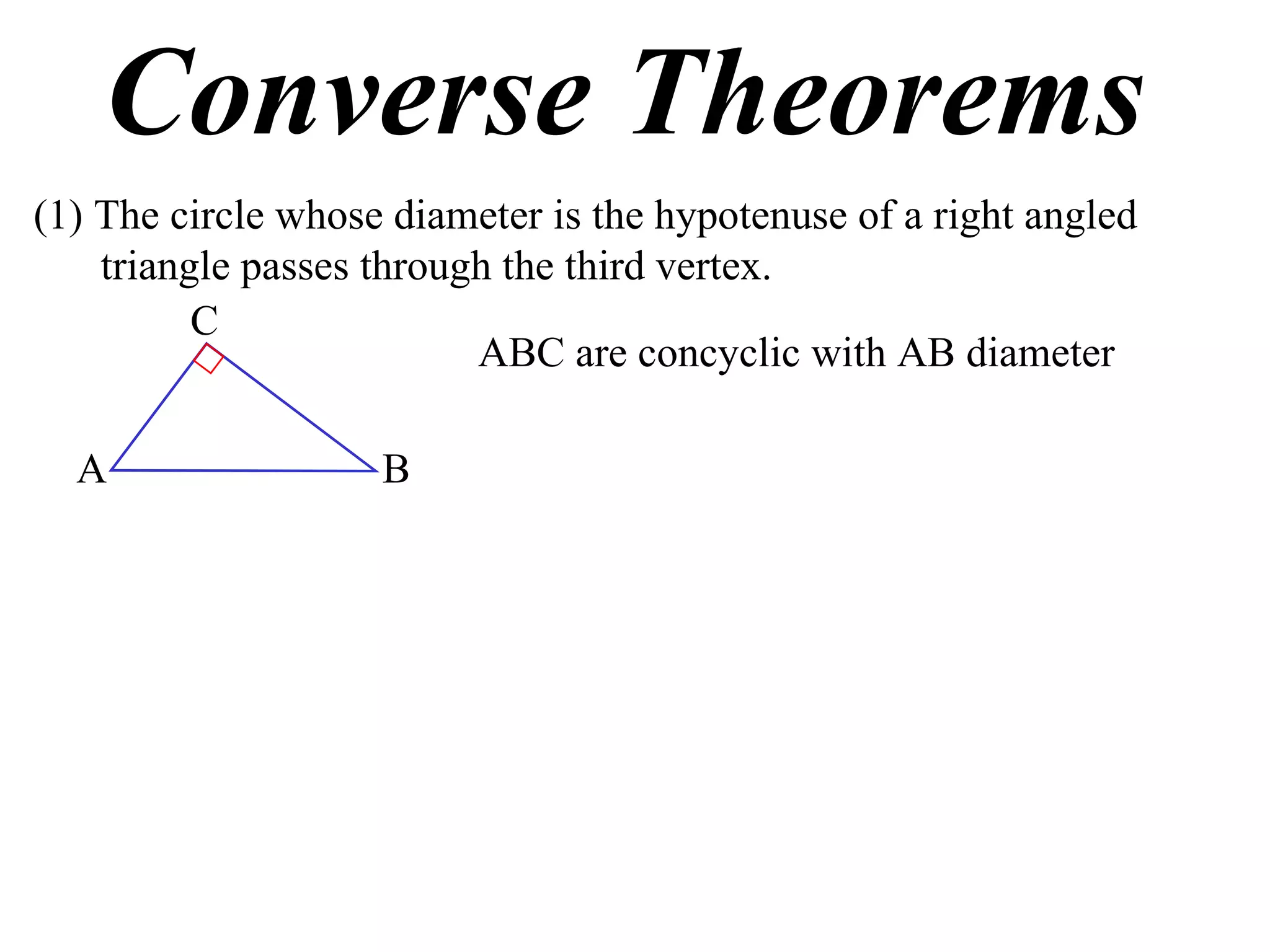
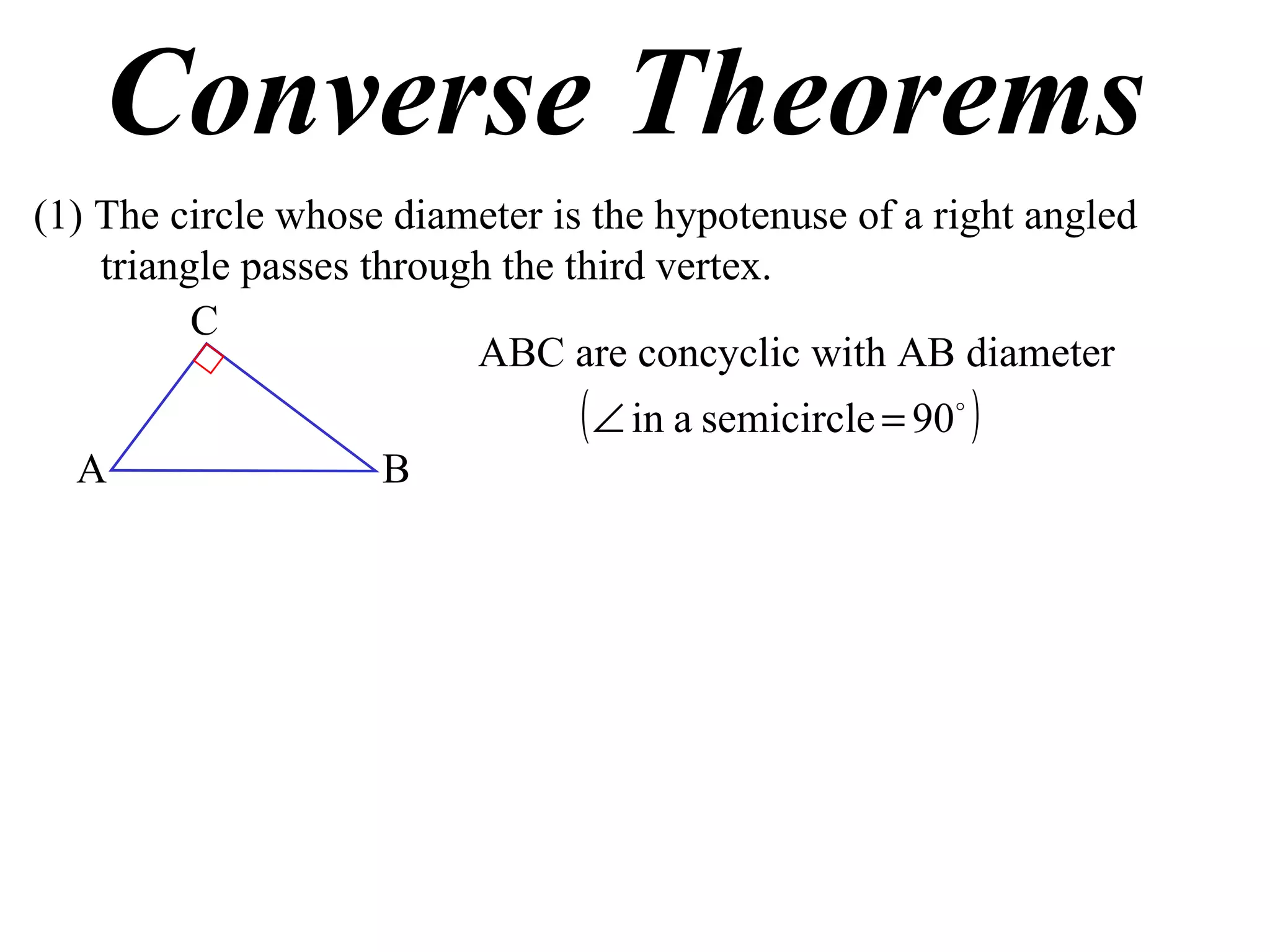
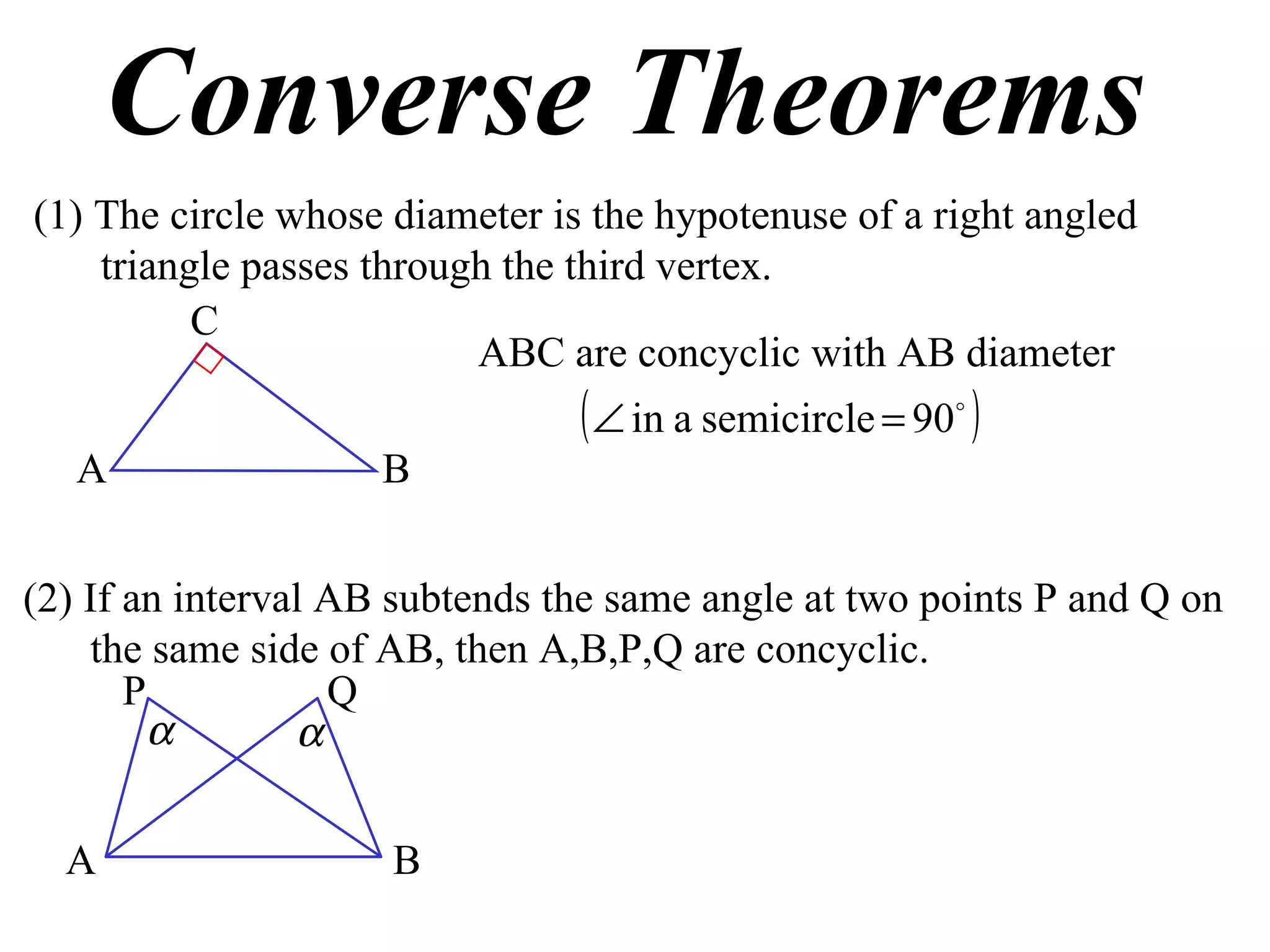
The document outlines three converse theorems regarding cyclic quadrilaterals: 1) If a right triangle's hypotenuse is used as the diameter of a circle, the circle will pass through the third vertex of the triangle. 2) If two points on the same side of a line segment make the same angle with the line segment, the four points are concyclic. 3) If a pair of opposite angles in a quadrilateral are supplementary, or if an exterior angle equals the opposite interior angle, then the quadrilateral is cyclic.

1. Converse Theorems

2. Converse Theorems (1) The circle whose diameter is the hypotenuse of a right angled triangle passes through the third vertex.

3. Converse Theorems (1) The circle whose diameter is the hypotenuse of a right angled triangle passes through the third vertex. A B C

4. Converse Theorems (1) The circle whose diameter is the hypotenuse of a right angled triangle passes through the third vertex. ABC are concyclic with AB diameter A B C

5. Converse Theorems (1) The circle whose diameter is the hypotenuse of a right angled triangle passes through the third vertex. ABC are concyclic with AB diameter A B C

6. Converse Theorems (1) The circle whose diameter is the hypotenuse of a right angled triangle passes through the third vertex. ABC are concyclic with AB diameter (2) If an interval AB subtends the same angle at two points P and Q on the same side of AB, then A,B,P,Q are concyclic. A B C

7. Converse Theorems (1) The circle whose diameter is the hypotenuse of a right angled triangle passes through the third vertex. ABC are concyclic with AB diameter (2) If an interval AB subtends the same angle at two points P and Q on the same side of AB, then A,B,P,Q are concyclic. A B C A B P Q

8. Converse Theorems (1) The circle whose diameter is the hypotenuse of a right angled triangle passes through the third vertex. ABC are concyclic with AB diameter (2) If an interval AB subtends the same angle at two points P and Q on the same side of AB, then A,B,P,Q are concyclic. ABQP is a cyclic quadrilateral A B C A B P Q

9. Converse Theorems (1) The circle whose diameter is the hypotenuse of a right angled triangle passes through the third vertex. ABC are concyclic with AB diameter (2) If an interval AB subtends the same angle at two points P and Q on the same side of AB, then A,B,P,Q are concyclic. ABQP is a cyclic quadrilateral A B C A B P Q

10. (3) If a pair of opposite angles in a quadrilateral are supplementary (or if an exterior angle equals the opposite interior angle) then the quadrilateral is cyclic.

11. (3) If a pair of opposite angles in a quadrilateral are supplementary (or if an exterior angle equals the opposite interior angle) then the quadrilateral is cyclic. A D B C

12. (3) If a pair of opposite angles in a quadrilateral are supplementary (or if an exterior angle equals the opposite interior angle) then the quadrilateral is cyclic. ABCD are concyclic A D B C

13. (3) If a pair of opposite angles in a quadrilateral are supplementary (or if an exterior angle equals the opposite interior angle) then the quadrilateral is cyclic. ABCD are concyclic A D B C

14. (3) If a pair of opposite angles in a quadrilateral are supplementary (or if an exterior angle equals the opposite interior angle) then the quadrilateral is cyclic. ABCD are concyclic Exercise 9D; 1, 2, 3, 6b, 7b, 10a, 11 A D B C