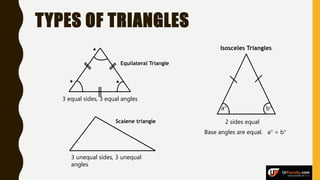
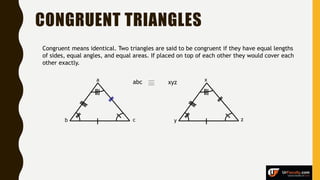
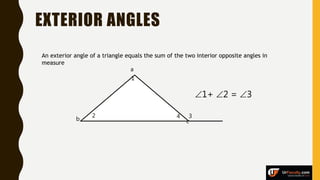
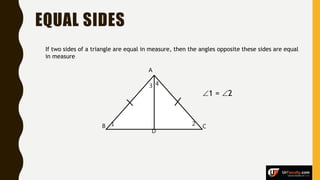
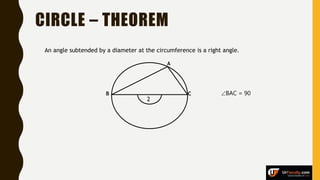
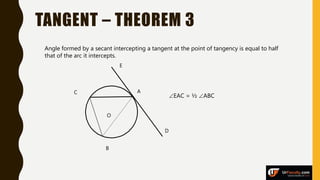
The document provides an overview of various types of triangles, including equilateral, isosceles, and scalene triangles, along with the properties of congruent triangles. It also discusses key circle theorems, such as the relationship between angles at the center and circumference, properties of tangents, and chord bisection by a diameter. These geometric principles are significant in understanding triangle and circle properties.

1. T R I A N G L E S & C I R C L E S

2. TYPES OF TRIANGLES
Equilateral Triangle
.
.
.
3 equal sides, 3 equal angles
Isosceles Triangles
a b
2 sides equal
Base angles are equal. a = b
Scalene triangle
3 unequal sides, 3 unequal
angles

3. CONGRUENT TRIANGLES
a
b c
x
y z
abc xyz
Congruent means identical. Two triangles are said to be congruent if they have equal lengths
of sides, equal angles, and equal areas. If placed on top of each other they would cover each
other exactly.

4. EXTERIOR ANGLES
a
b c
3
1
2 4
An exterior angle of a triangle equals the sum of the two interior opposite angles in
measure
1+ 2 = 3

5. EQUAL SIDES
A
B C1 2
D
3 4
If two sides of a triangle are equal in measure, then the angles opposite these sides are equal
in measure
1 = 2

6. CIRCLE (ARC THEOREM)
D
A
B C
O
The measure of the angle at the centre of the circle is twice the measure of the angle at the
circumference, standing on the same arc.
BOC = 2 BAC

7. CIRCLE (ARC THEOREM)
A
B
C
D
3
1
2
All angles at the circumference on the same arc are equal in measure.
BAC= BDC

8. CIRCLE – THEOREM
An angle subtended by a diameter at the circumference is a right angle.
A
B C
2
BAC = 90

9. CIRCLE – THEOREM
A line through the centre of a circle perpendicular to a chord bisects the chord
A
B
C
D
∟
∟
1
2
AD = BD

10. TANGENT – THEOREM 1
If line l is the tangent to the circle with center O, meeting the circle at point A. Then OA is
perpendicular to the tangent l
OA is perpendicular to the tangent l
O
A
l

11. TANGENT – THEOREM 2
If two segments from the same exterior point T are tangent to the circle, then they are equal
in length.
TA = TB
O
A
T
B

12. TANGENT – THEOREM 3
Angle formed by a secant intercepting a tangent at the point of tangency is equal to half
that of the arc it intercepts.
EAC = ½ ABC
O
A
D
B
E
C

13. WATCH OUR VIDEO TUTORIALS FOR
MORE PROBLEMS