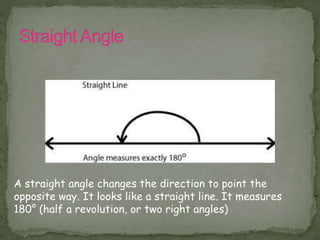
This document defines and describes various lines and angles that are important concepts in geometry. It defines basic terms like rays, lines, line segments, intersecting and non-intersecting lines. It also defines and provides examples of different types of angles like acute angles, right angles, obtuse angles, and their properties in relation to parallel and intersecting lines. Key angle relationships that are discussed include corresponding angles, alternate interior angles, alternate exterior angles, and interior angles formed by a transversal cutting parallel lines.

2. Lines And Angles

3.  Introduction
 Angles In Daily Life
 Basic Terms And Definitions
 Points
 Intersecting Lines And Non Intersecting Lines
 Perpendicular Lines
 Angles
 Parallel Lines And A Transversal

4.  In math geometry the lines and angles are
important tools. If any object in ideal,
that is called as line and it is represented
as straight curve.
 The angle is related with line that is the
cross-section of two-line is create the
angle and that intersection point is called
as vertex. Here we see about types of line
and angle in math.

5. If we look around us, we will see angles everywhere.

6. •RAY: A part of a line, with one endpoint, that continues
without end in one direction
•LINE: A straight path extending in both directions with no
endpoints
•LINE SEGMENT: A part of a line that includes two
points, called endpoints, and all the points between them
Basic Terms And Definition

7. Intersecting Lines : Lines that cross
Non Intersecting lines : Lines that never cross and are always
the same distance apart

8. • Hardwood Floor
• Opposite sides of windows, desks, etc.
• Parking slots in parking lot
• Parallel Parking
• Streets: Laramie & LeClaire

9. Two lines that intersect to form four right angles

10. •Window Panes
•Streets Of Cities

11. In geometry, an angle is the figure formed by two rays sharing a
common endpoint, called the vertex of the angle. The magnitude of the
angle is the "amount of rotation" that separates the two rays, and can
be measured by considering the length of circular arc swept out when
one ray is rotated about the vertex to coincide with the other.
•Acute Angle
•Right Angle
•Obtuse Angle
•Straight angle
•Reflex Angle
•Adjacent Angles
•Linear Pair Of Angles
•Vertically Opposite Angles

12. The measure of an angle with a measure between 0° and
90° or with less than 90° radians.

14. An angle formed by the perpendicular intersection of
two straight lines; an angle of 90°.

16. Angle measures greater than 90 degrees but less than
180 degrees.

18. A straight angle changes the direction to point the
opposite way. It looks like a straight line. It measures
180° (half a revolution, or two right angles)

20. A Reflex Angle is more than 180° but less than 360°

21. In geometry, adjacent angles, often shortened as adj. ∠s,
are angles that have a common ray coming out of the vertex
going between two other rays. In other words, they are
angles that are side by side, or adjacent.

22. A pair of adjacent angles formed by intersecting lines.
Linear pairs of angles are supplementary.

23. In geometry, a pair of angles is said to
be vertical (also opposite and vertically opposite, which is abbreviated
as vert. opp. ∠s ) if the angles are formed from two
intersecting lines and the angles are not adjacent. They all share a
vertex. Such angles are equal in measure and can be described
as congruent.

24. Transversal :- A transversal, or a
line that intersects two or more coplanar
lines, each at a different point, is a very
useful line in geometry. Transversals
tell us a great deal about angles.
Parallel Lines :- Parallel lines remain the same distance apart over their
entire length. No matter how far you extend them, they will never meet.
•Corresponding Angles
•Alternate Interior Angles
•Alternate Exterior Angles
•Interior Angles On The Same Side Of the transversal

25. The angles that occupy the same relative position at
each intersection where a straight line crosses two
others. If the two lines are parallel, the corresponding
angles are equal.

26. When two parallel lines are cut by a transversal, the two
pairs of angles on opposite sides of the transversal and
inside the parallel lines, and the angles in each pair are
congruent.

27. When two parallel lines are cut by a transversal, the two
pairs of angles on opposite sides of the transversal and
outside the parallel lines, and the angles in each pair are
congruent.

28. Interior angles on the same side of the transversal are also referred
to as consecutive interior angles or allied angles or co-interior angles.
Further, many a times, we simply use the words alternate angles for
alternate interior angles.