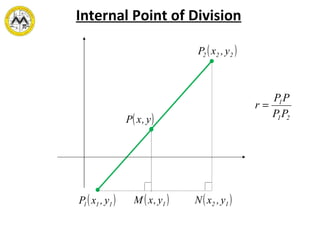
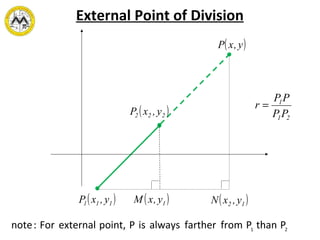
This document discusses dividing line segments into equal parts and finding points of division. It defines the median of a triangle as the line segment joining a vertex to the midpoint of the opposite side. It provides examples of finding division points, midpoints, and points that are a certain fraction of the distance between two points. Finally, it gives a triangle and asks to find the points on each median that are two-thirds of the distance from the vertex to the midpoint of the opposite side.

1. ANALYTIC GEOMETRY (Lesson 4) Math 14 Plane and Analytic Geometry

2. OBJECTIVES : At the end of the lesson, the student is expected to be able to: • Determine the coordinates of a point of division of a line segment. • Define the median of the triangle.

3. DIVISION OF A LINE SEGMENT

4. Internal Point of Division

5. External Point of Division

7. Examples : The line segment joining (-5, -3) and (3, 4) is to be divided into five equal parts. Find the point of division closest to (-5, -3). Find the midpoint of the segment joining (7, -2) and (-3, 5). The line segment from (1, 4) to (2, 1) is extended a distance equal to twice its length. Find the terminal point. On the line joining (4, -5) to (-4, -2), find the point which is three-seventh the distance from the first to the second point. Find the trisection points of the line joining (-6, 2) and (3, 8).

8. 6. The line segment joining a vertex of a triangle and the midpoint of the opposite side is called the median of the triangle. Given a triangle whose vertices are A(4,-4), B(10, 4) and C(2, 6), find the point on each median that is two-thirds of the distance from the vertex to the midpoint of the opposite side.

9. REFERENCES Analytic Geometry, 6 th Edition, by Douglas F. Riddle Analytic Geometry, 7 th Edition, by Gordon Fuller/Dalton Tarwater Analytic Geometry, by Quirino and Mijares