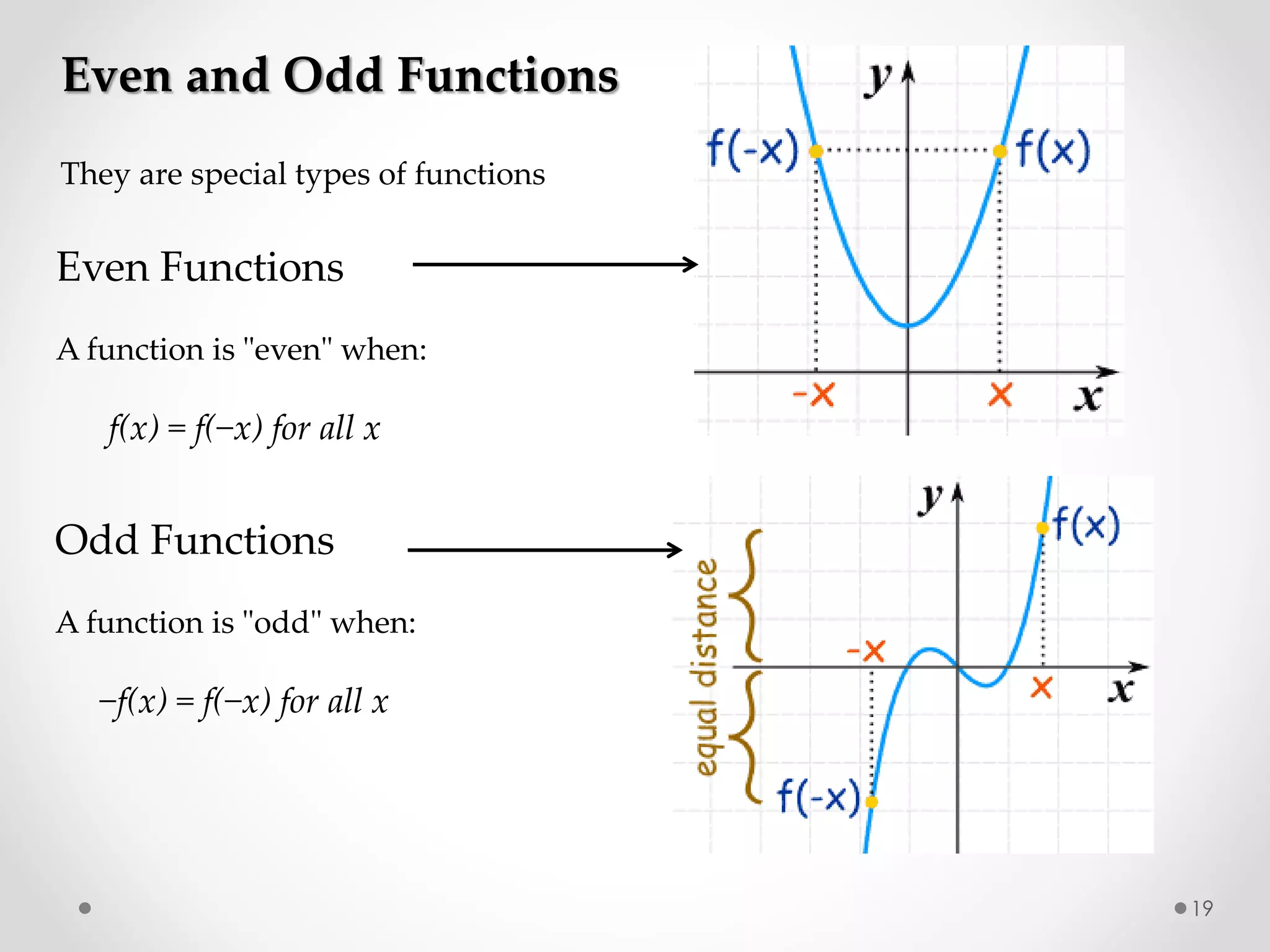
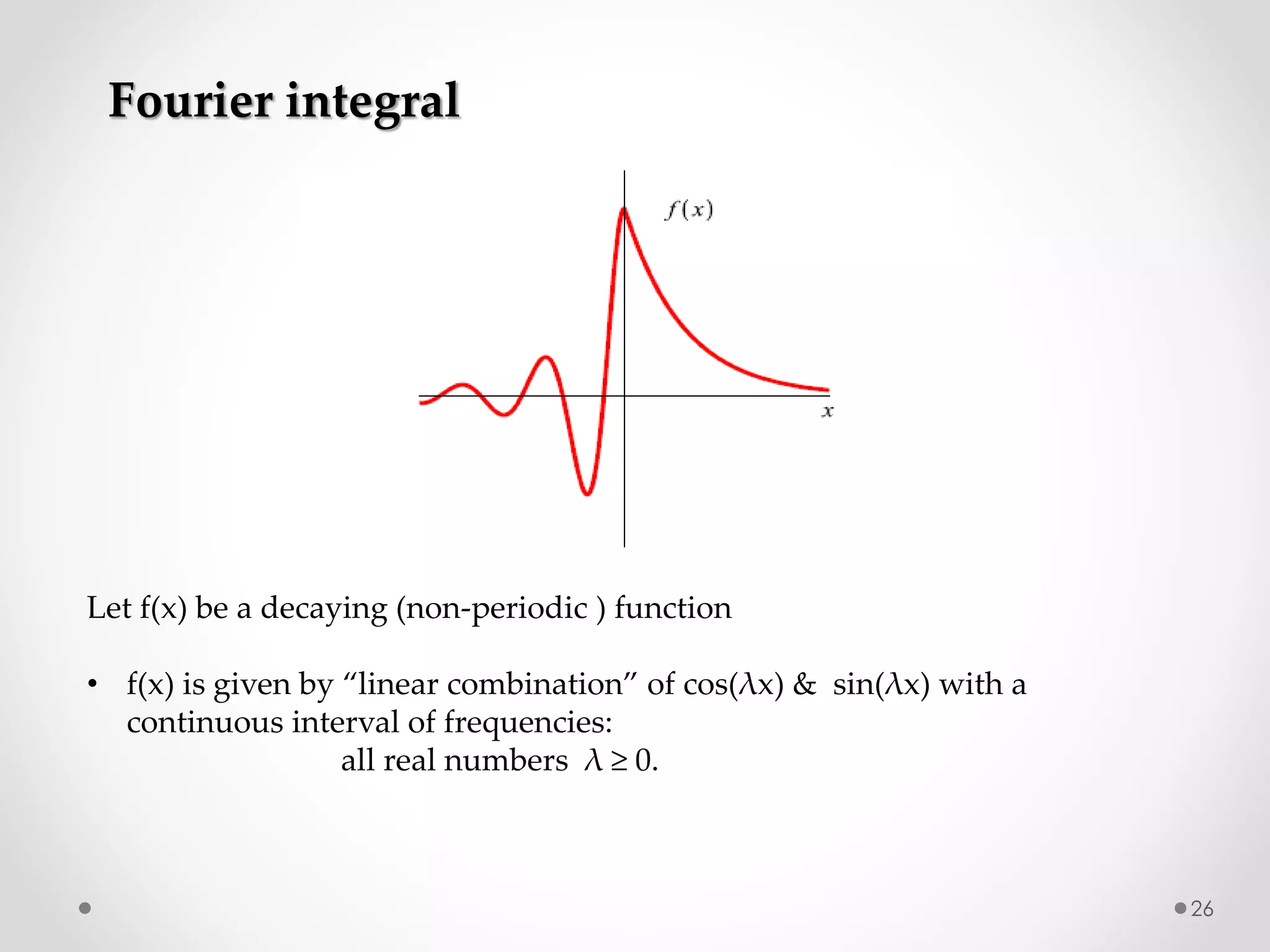
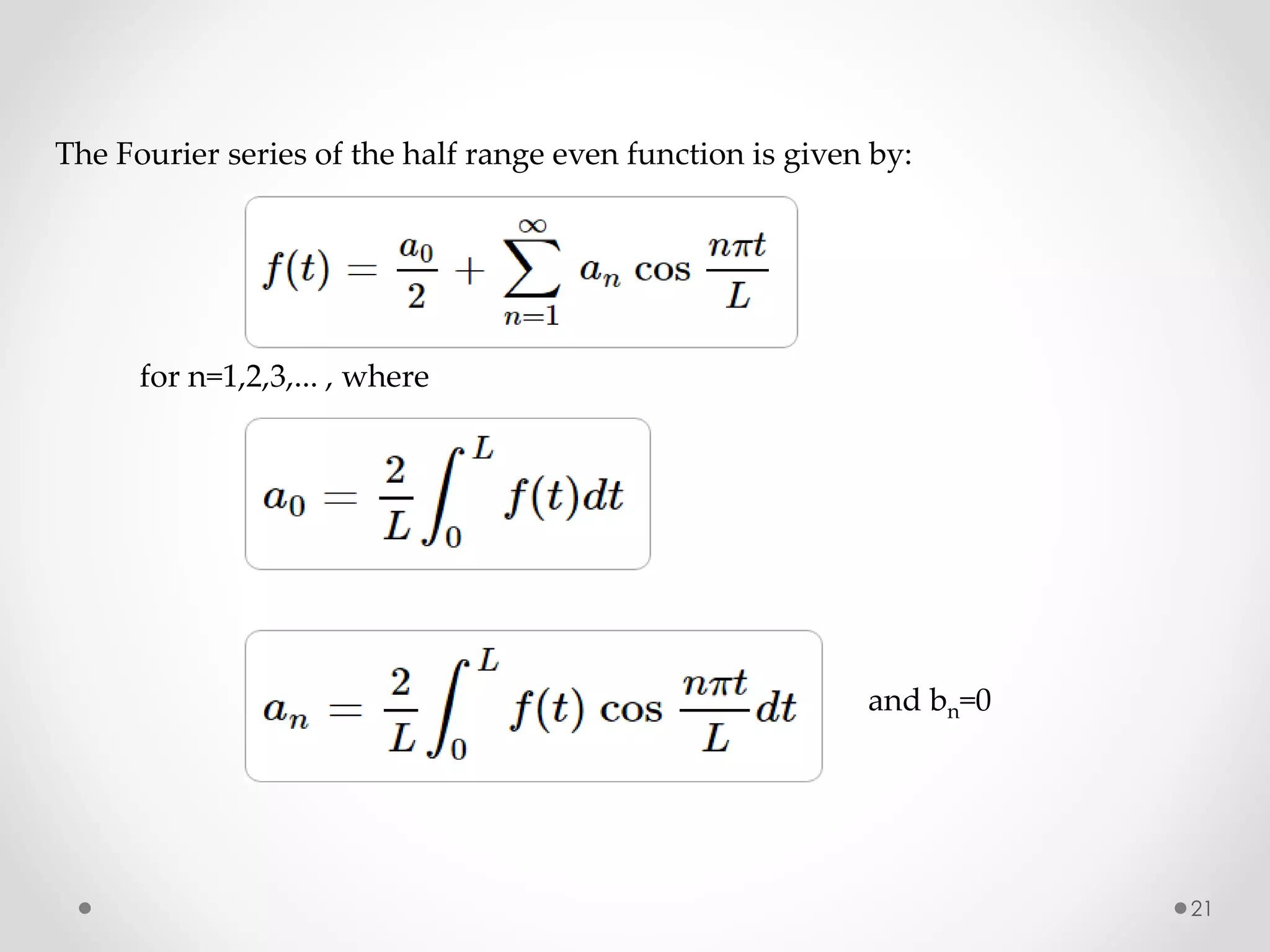The document discusses various special functions used in engineering and mathematics. It begins with an introduction to beta and gamma functions, Bessel functions, error functions, Heaviside's unit step function, pulse functions, sinusoidal pulses, and other periodic functions. It then explains Fourier series and their applications for representing periodic functions as infinite sums of sines and cosines. Specifically, it discusses even and odd functions, half-range expansions, and using Fourier series to model forced oscillations. Finally, the document briefly introduces the Fourier integral as representing a function as a continuous range of frequencies.

1. SHANTILAL SHAH GOVERNMENT
ENGINEERING COLLEGE
Postal Address : New Sidsar Campus
Post : Vartej, Sidsar, Bhavnagar-364060, Gujarat, India
Contact : 0278-2445509,2445767 Fax : 0278-2445509
Website: http://www.ssgec.ac.in/
Sr.no Roll no. Enrollment no. Name
1. 3017 140430117019 JITIN J PILLAI
2. 3010 140430117012 DODIYA PARTH
3. 3007 140430117008 CHAUHAN ASHISH
4. 3018 140430117020 JOSHI MEET
5. 3002 140430117002 BAVISHI BIRJU
SEMESTER: 3RD
BRANCH : INSTRUMENTATION & CONTROL
BATCH : B1
Group members :
Enrollment no.

2. INTRODUCTION TO SOME
SPECIAL FUNCTIONS
2

3.  Beta & Gamma functions
 Bessel function
 Error function & Complementary error function
 Heaviside's Unit Step Function
 Pulse Unit Height & Duration
 Sinusoidal pulse
 Rectangle function
 Gate function
 Dirac Delta function
 Signum function
 Saw tooth wave function
 Triangular wave function
 Half-wave Rectifed Sinusoidal function
 Full-wave Rectifed Sinusoidal function
 Square wave function
3

4. Beta function
Bessel function
Gamma functions
4

5. Error function
5

6. Complementary error function
6

7. Heaviside's Unit Step Function
7

8. Pulse Unit Height & Duration
Sinusoidal Pulse
8

9. Rectangle function
Gate function
9

10. Dirac Delta function
10

11. Signum function
11

12. Saw tooth wave function
12

13. Triangular wave function
Half-wave Rectifed Sinusoidal function
13

14. Full-wave Rectifed Sinusoidal function
Square wave function
14

15. FOURIER SERIES & FOURIER
INTEGRAL
15

16. 16
 Periodic function
 Trigonometric series
 Fourier series
 Even and odd functions
 Half-range Expansion
 Applications of Fourier series: Forced oscillations
 Fourier integral

17. A function f is said to be periodic with period P (P being a nonzero constant)
if we have
for all values of x in the domain.
Periodic function
Trigonometric series
A trigonometric series is a series of the form:
It is called a Fourier series if the terms and have the form:
where f is an integrable function.
17

18. 18
A Fourier series is an expansion of
a periodic function f(x) in terms of
an infinite sum of sines and
cosines.
Fourier series
With a Fourier series we are going to try to write a series representation
for on in the form,
So, a Fourier series is, in some way a combination of the Fourier sine and
Fourier cosine series.

19. 19
Even and Odd Functions
They are special types of functions
Even Functions
A function is "even" when:
f(x) = f(−x) for all x
Odd Functions
A function is "odd" when:
−f(x) = f(−x) for all x

20. 20
If a function is defined over half the range, say 0 to L, instead of the full range
from −L to L, it may be expanded in a series of sine terms only or of cosine terms
only. The series produced is then called a Half Range Fourier series.
Half-range Expansion
Conversely, the Fourier Series of an even or odd function can be analysed
using the half range definition.
An even function can be expanded using half its range from
0 to L or
−L to 0 or
L to 2L
That is, the range of integration is L.
Even function Half-range Expansion

21. 21
The Fourier series of the half range even function is given by:
for n=1,2,3,... , where
and bn=0

22. 22
Odd function Half-range Expansion
An odd function can be expanded using half its range from 0 to L, i.e. the range
of integration has value L. The Fourier series of the odd function is:
Since ao = 0 and an = 0, we have:

23. 23
Applications of Fourier series : Forced
Oscillations
 Consider a mass-spring system as before, where we have a mass m on a
spring with spring constant k , with damping c , and a force F (t) applied to
the mass. Suppose the forcing function F (t) is 2L -- periodic for some L > 0 .
The equation that governs this particular setup is :

24. 24
 The general solution consists of the complementary solution xc , which solves
the associated homogeneous equation mx ′′ + cx′ + kx = 0 , and a particular
solution we call xp .
 For c > 0 , the complementary solution xc will decay as time goes by.
Therefore, we are mostly interested in a particular solution xp that does not
decay and is periodic with the same period as F (t) .
 We call this particular solution the steady periodic solution and we write it as
xsp as before. What will be new in this section is that we consider an arbitrary
forcing function F (t) instead of a simple cosine.
 For simplicity, let us suppose that c = 0 . The problem with c > 0 is very similar.
The equation
has the general solution

25. 25
 In the spirit of the last section and the idea of undetermined coefficients we
first write
 Then we write a proposed steady periodic solution x as
where an and bn are unknowns. We plug x into the
differential equation and solve for an and bn in terms of cn
and dn .

26. 26
Fourier integral
Let f(x) be a decaying (non-periodic ) function
• f(x) is given by “linear combination” of cos(λx) & sin(λx) with a
continuous interval of frequencies:
all real numbers λ ≥ 0.

27. 27
Fourier integral:
Fourier integral formula:
Convergence Theorem:

28. 28
References
INTERNET :
https://en.wikipedia.org/wiki/List_of_mathematical_series
https://en.wikipedia.org/wiki/Fourier_series
https://en.wikipedia.org/wiki/Fourier_integral_operator
people.math.gatech.edu/~xchen/teach/real.../Fourier_integral_intro.pdf
math.mit.edu/cse/websections/cse41.pdf
www.jirka.org/diffyqs/htmlver/diffyqsse29.html
https://people.math.osu.edu/kwa.1/notes/512_2.7.pdf
http://physics.bu.edu/~pankajm/PY501/fourier.pdf
http://mathworld.wolfram.com/PeriodicFunction.html
http://tutorial.math.lamar.edu/Classes/DE/FourierSeries.aspx
http://www.fourier-series.com/

29. 29
BOOKS :
• Elementary Differential Equations (8th Edition), by W. E. Boyce and R.
DiPrima, John Wiley (2005).
• Advanced Engineering Mathematics (9th Edition), by E. Kreyszig, Wiley-
India (2013).
• Advanced Engineering Mathematics, by Ravish R. Singh and Mukul Bhatt,
Mcgraw Hill Education (India) Pvt. Ltd.
References

30. 30