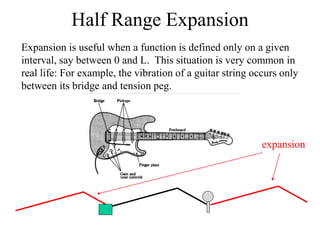
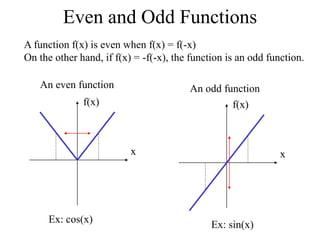
The document discusses Fourier series for functions with an arbitrary period p=2L. It explains that to define the Fourier series in this case, the variable x needs to be replaced with (π/L)x, so that when x=L, the new variable equals π and when x=-L it equals -π. This allows the previous Fourier series formulas to be used with this change of variable. It also discusses even and odd functions and how their Fourier series take the form of either a Fourier cosine series or Fourier sine series, and introduces the concept of a half range expansion which is useful when a function is only defined on a finite interval like between 0 and L.

1. Fourier series of function with arbitrary period p=2L
Instead of a period of 2, many functions have an arbitrary period,
say a period of 2L. In order to convert the Fourier series defined
earlier for these functions, a change of variable is needed:
Replace the variable x by (/L)x: when x=L the new variable
equals to ; when x= -L, it equals to - . Therefore, the previous
formulas can be used by simply making the change
0
1
0
( ) [ cos( ) sin( )]
1
( ) ,
2
1
( )cos( ) , 1,2
1
( )sin( ) , 1,2
n n
n
L
L
L
n
L
L
n
L
n n
f x a a x b x
L L
a f x dx
L
n x
a f x dx n
L L
n x
b f x dx n
L L
 







  

 
 





2. Even and Odd Functions
A function f(x) is even when f(x) = f(-x)
On the other hand, if f(x) = -f(-x), the function is an odd function.
An even function
x
f(x)
x
f(x)
An odd function
Ex: cos(x)
Ex: sin(x)

3. L 0 0
-L 0 0
0
0 0
0 0
- 0
If f(x) is an even function
f(x)dx ( ) ( ) ( ) ( ) ( )
( ) ( ) 2 ( )
If f(x) is an odd function, then
( ) ( ) ( ) ( ) ( ) ( )
L L
L L
L L
L
L L
L L L
f x dx f x dx f x d x f x dx
f x dx f x dx f x dx
f x dx f x dx f x dx f x d x f x dx



     
   

     
    
  
    0
0
0
( ) ( ) 0
If f(x) is even and g(x) is odd, then
h(x)=f(x)g(x) is an odd function
h(x)=f(x)g(x)=f(-x)[-g(-x)]=-[f(-x)g(-x)]=-h(-x)
L
L
L
f x dx f x dx
  


 

4. Fourier cosine and sine series
0
1
0 0
1 1
The Fourier series of an even function f(x) of period 2L is
a "Fourier cosine series"
( ) [ cos( )]
( ) [ cos( )] [ cos( )] ( )
The Fourier series of an odd func
n
n
n n
n n
n
f x a a x
L
n n
f x a a x a a x f x
L L

 


 
 

 
      


 
1
1 1
tion g(x) of period 2L is
a "Fourier sine series"
( ) [ sin( )]
( ) [ sin( )] [ sin( )] ( )
n
n
n n
n n
n
g x b x
L
n n
g x b x b x g x
L L

 


 
 

      

 

5. Half Range Expansion
Expansion is useful when a function is defined only on a given
interval, say between 0 and L. This situation is very common in
real life: For example, the vibration of a guitar string occurs only
between its bridge and tension peg.
expansion