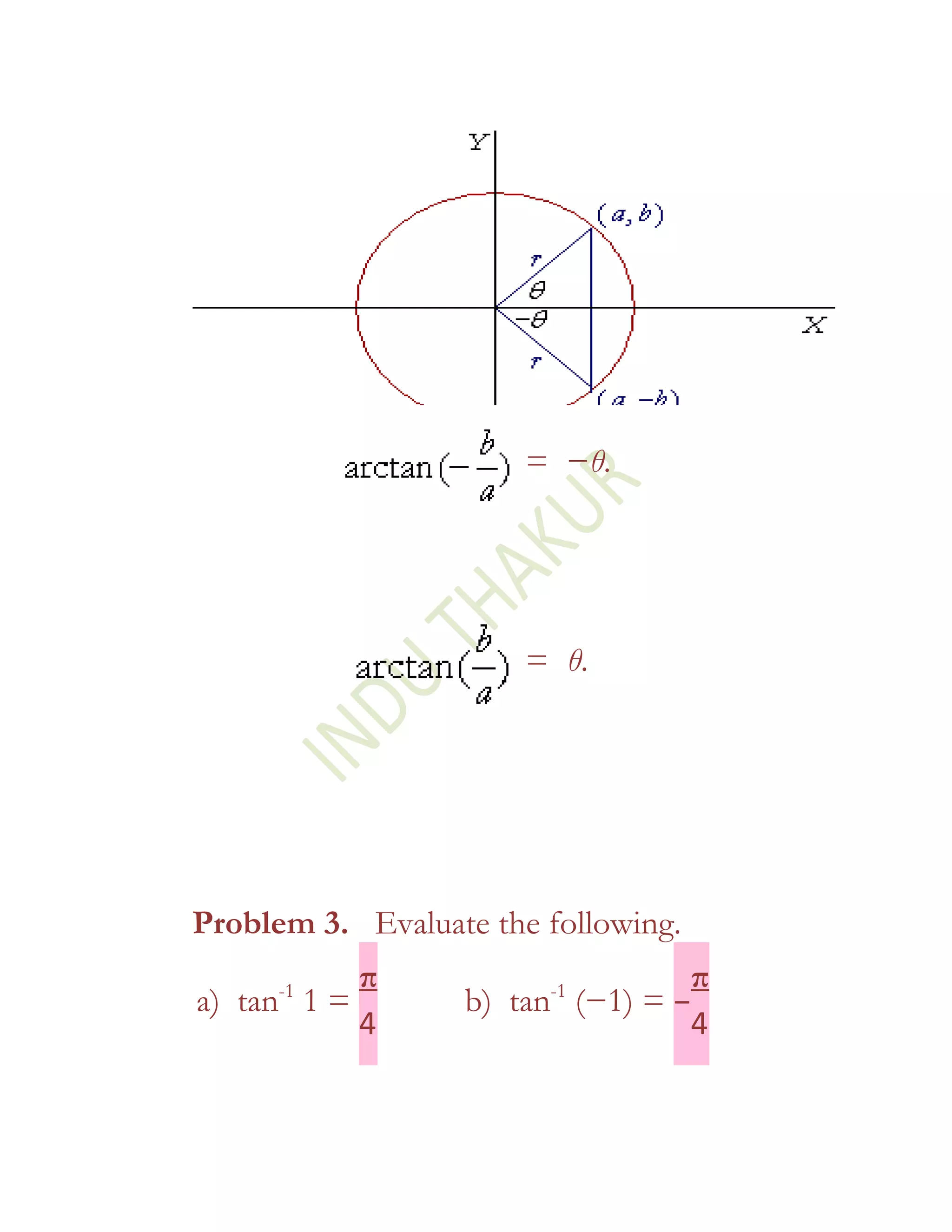
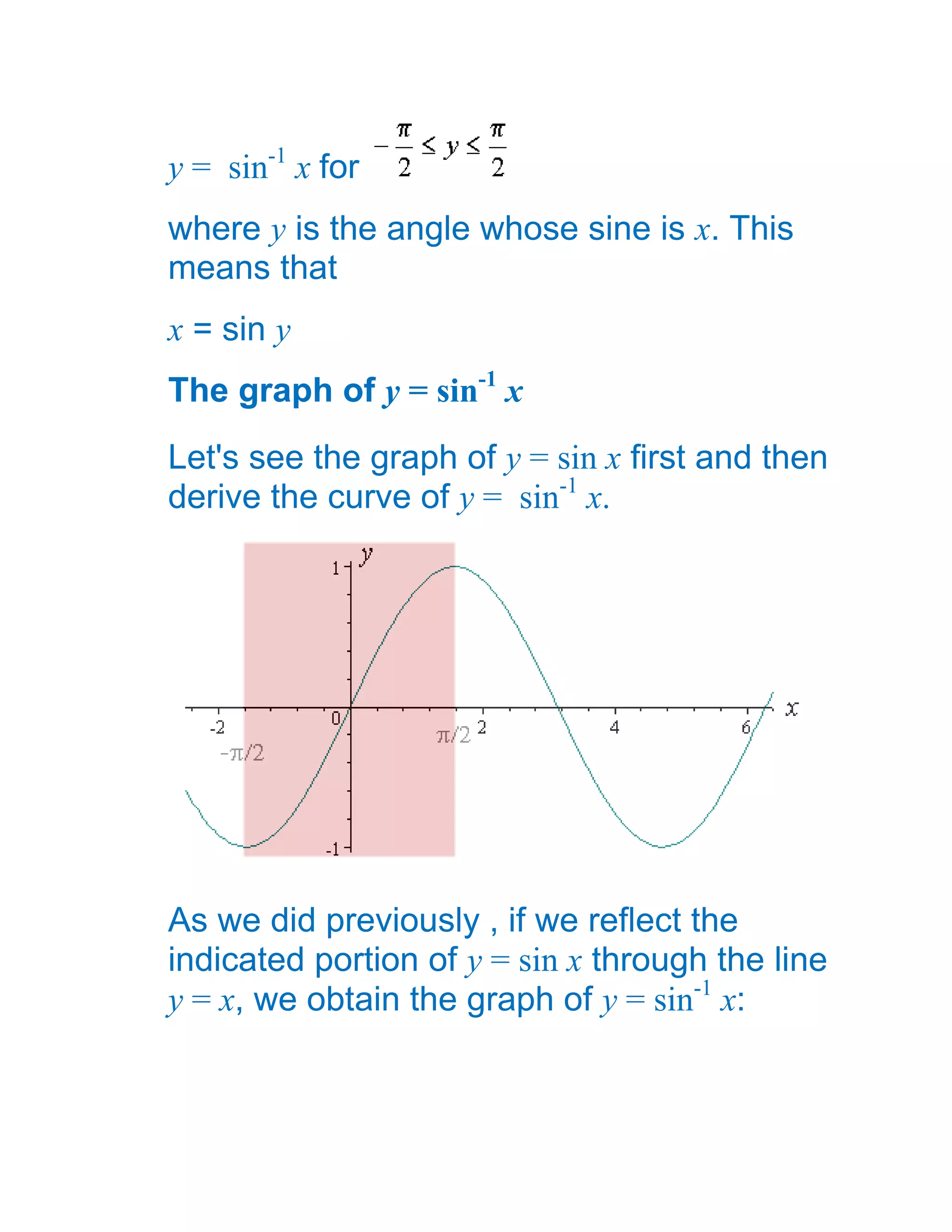
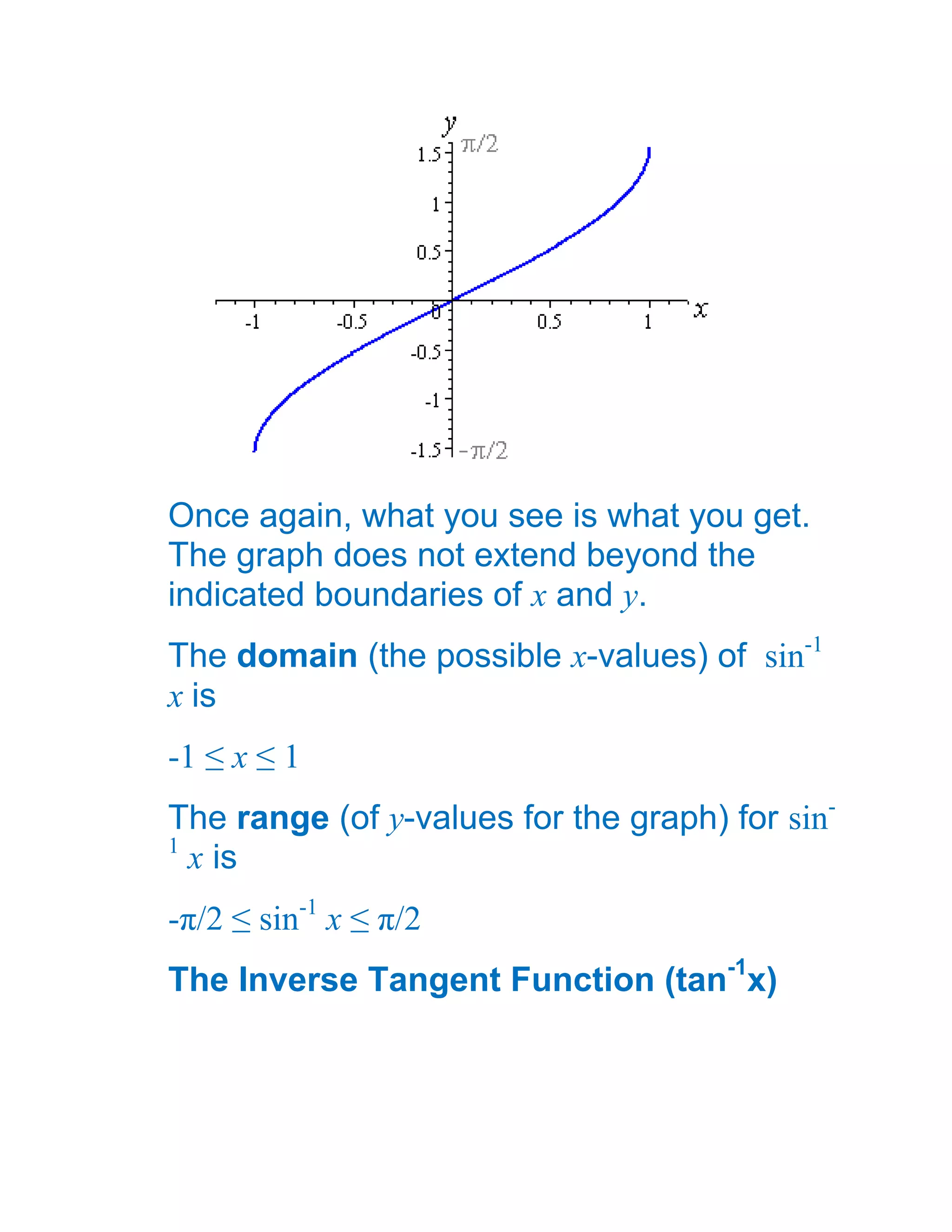
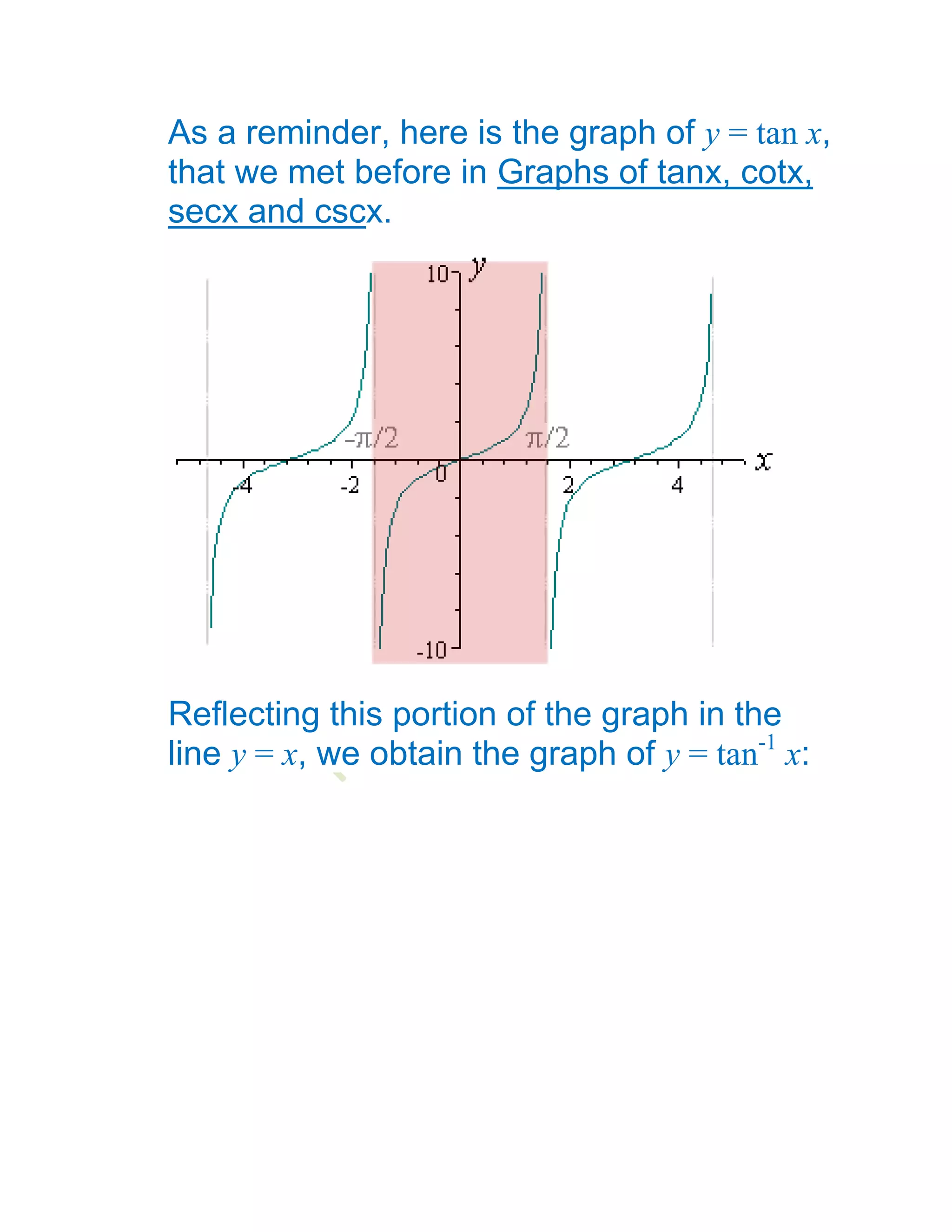
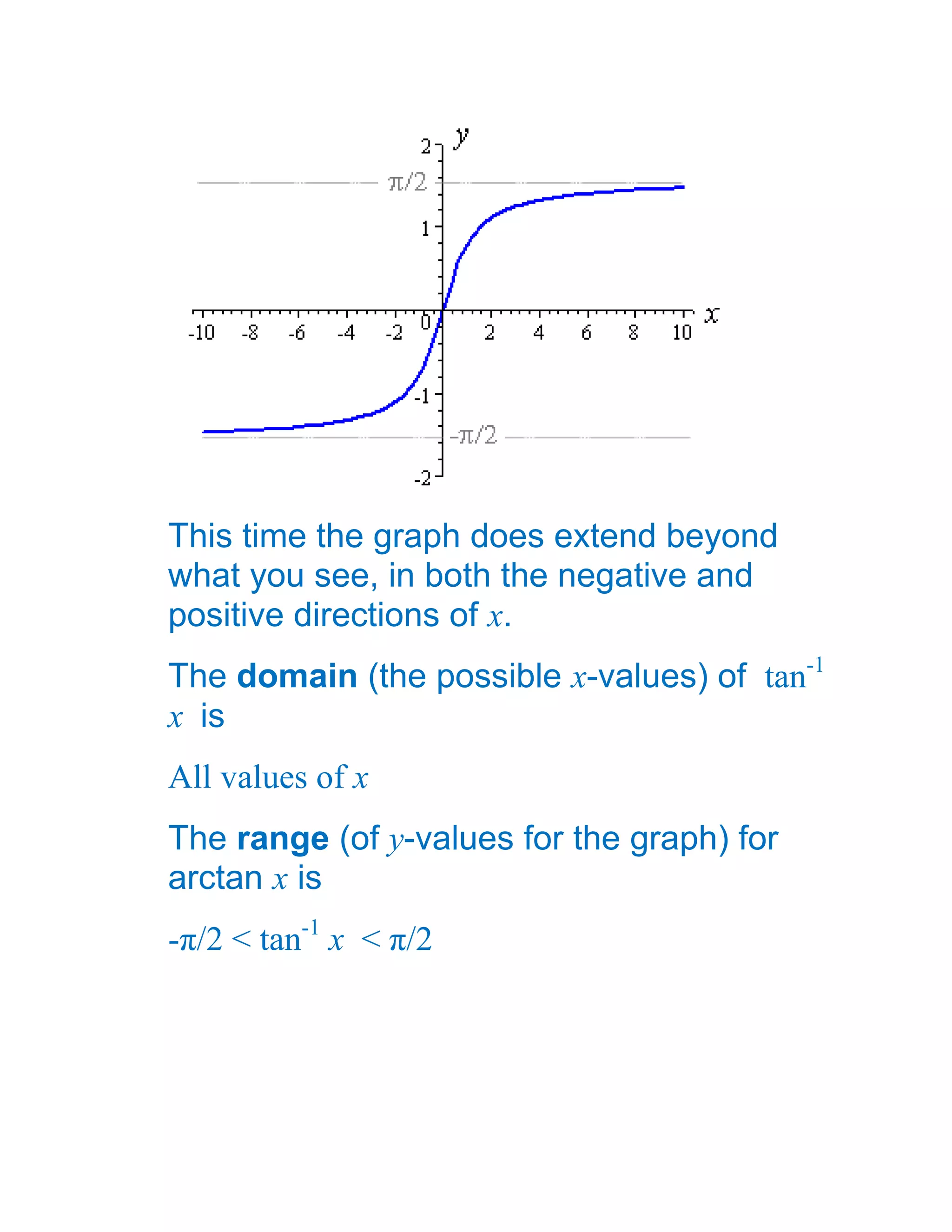
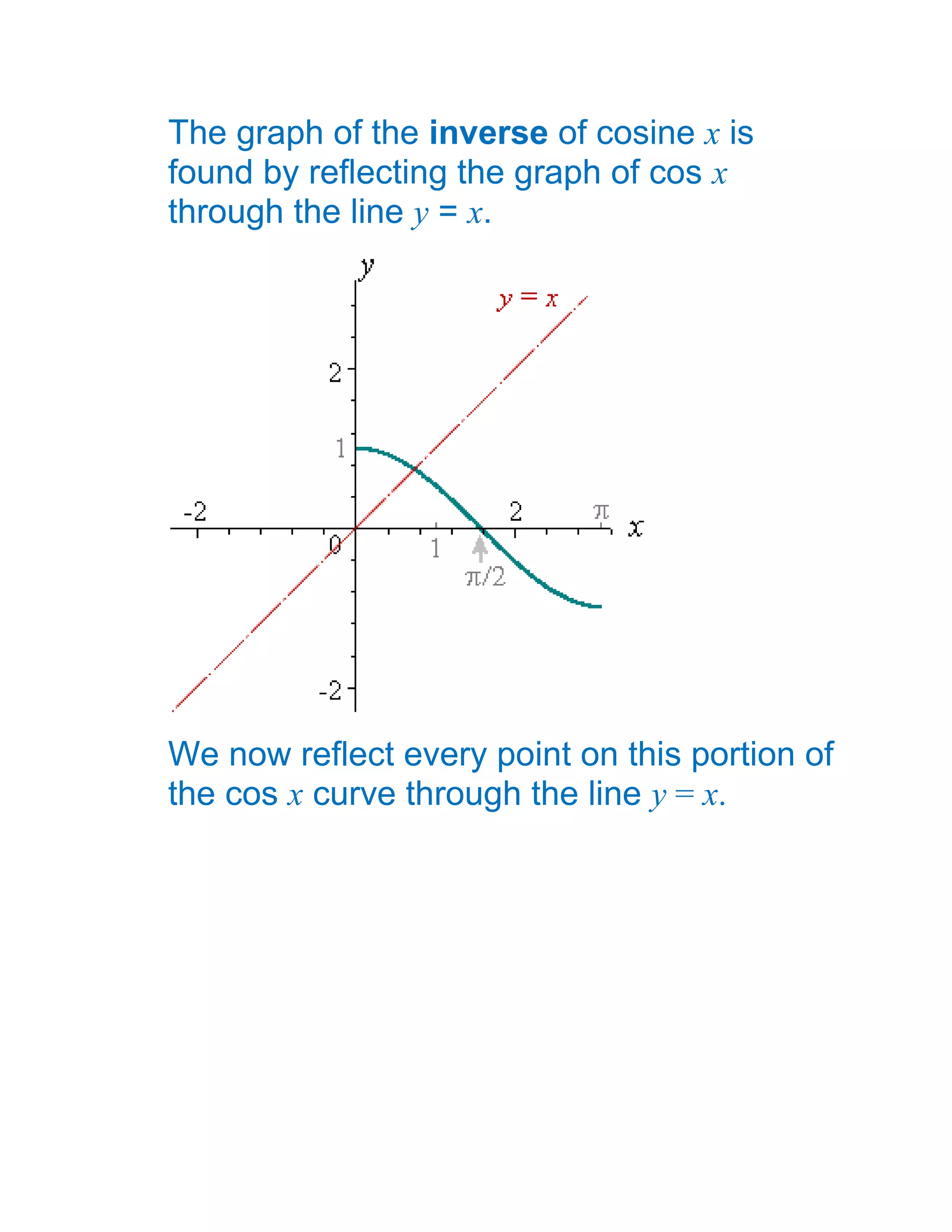
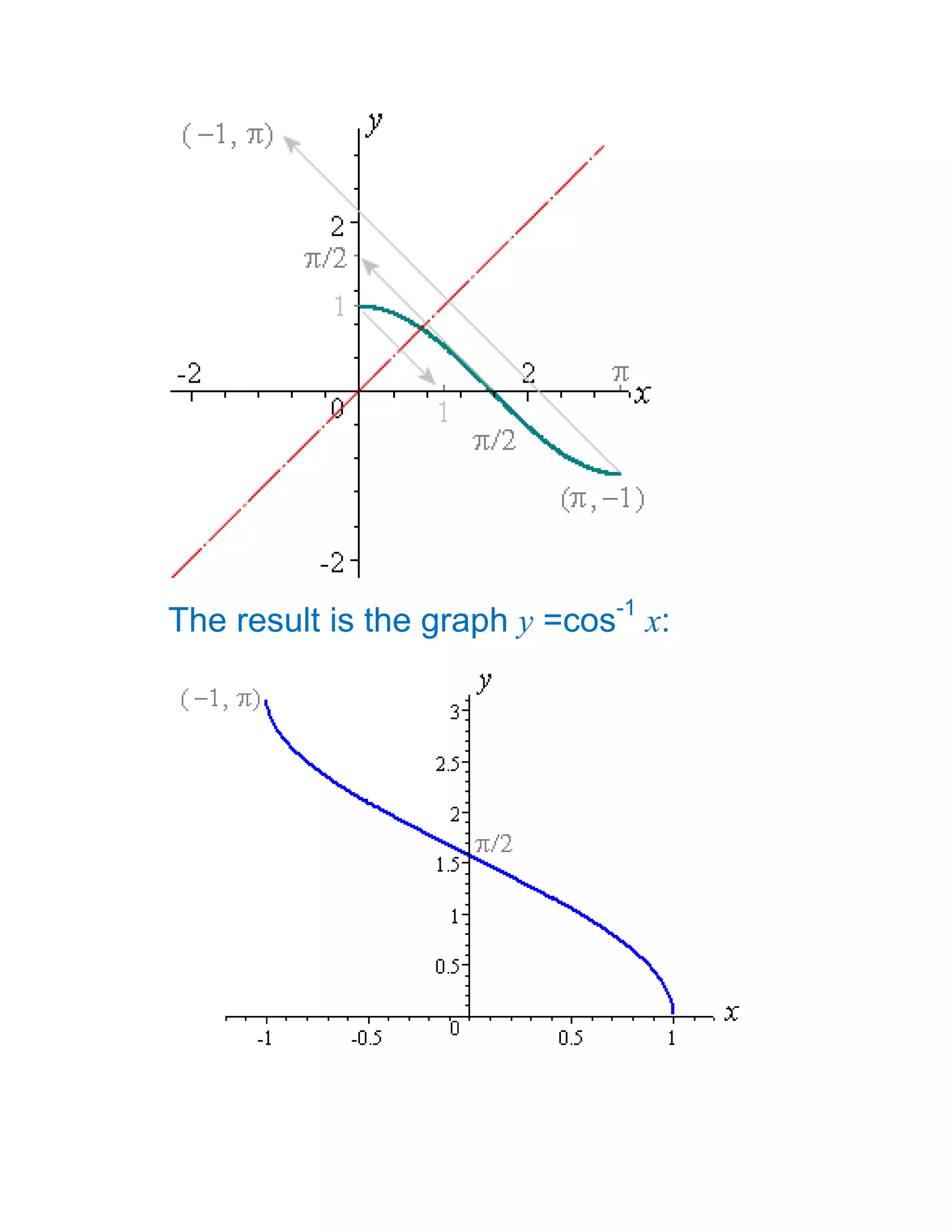
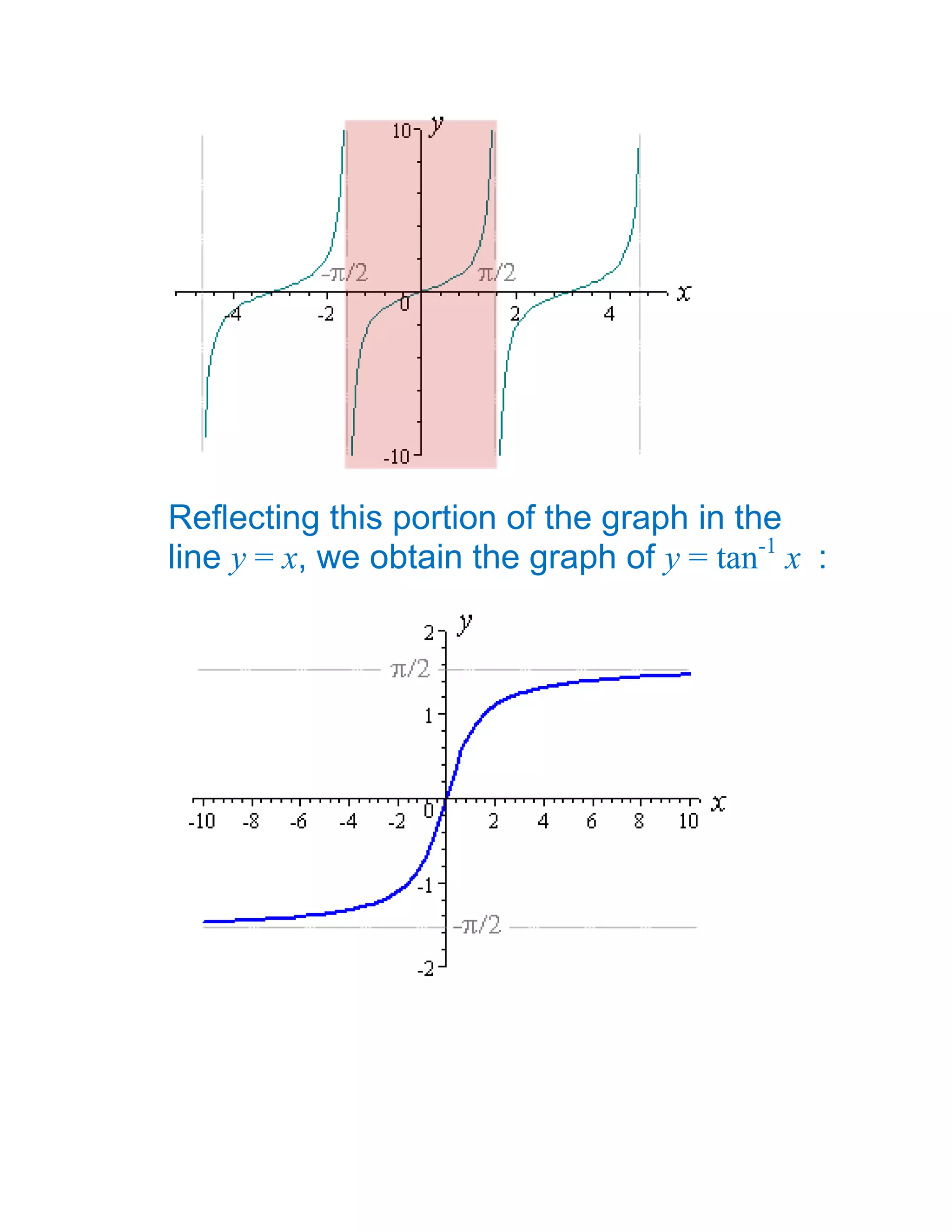
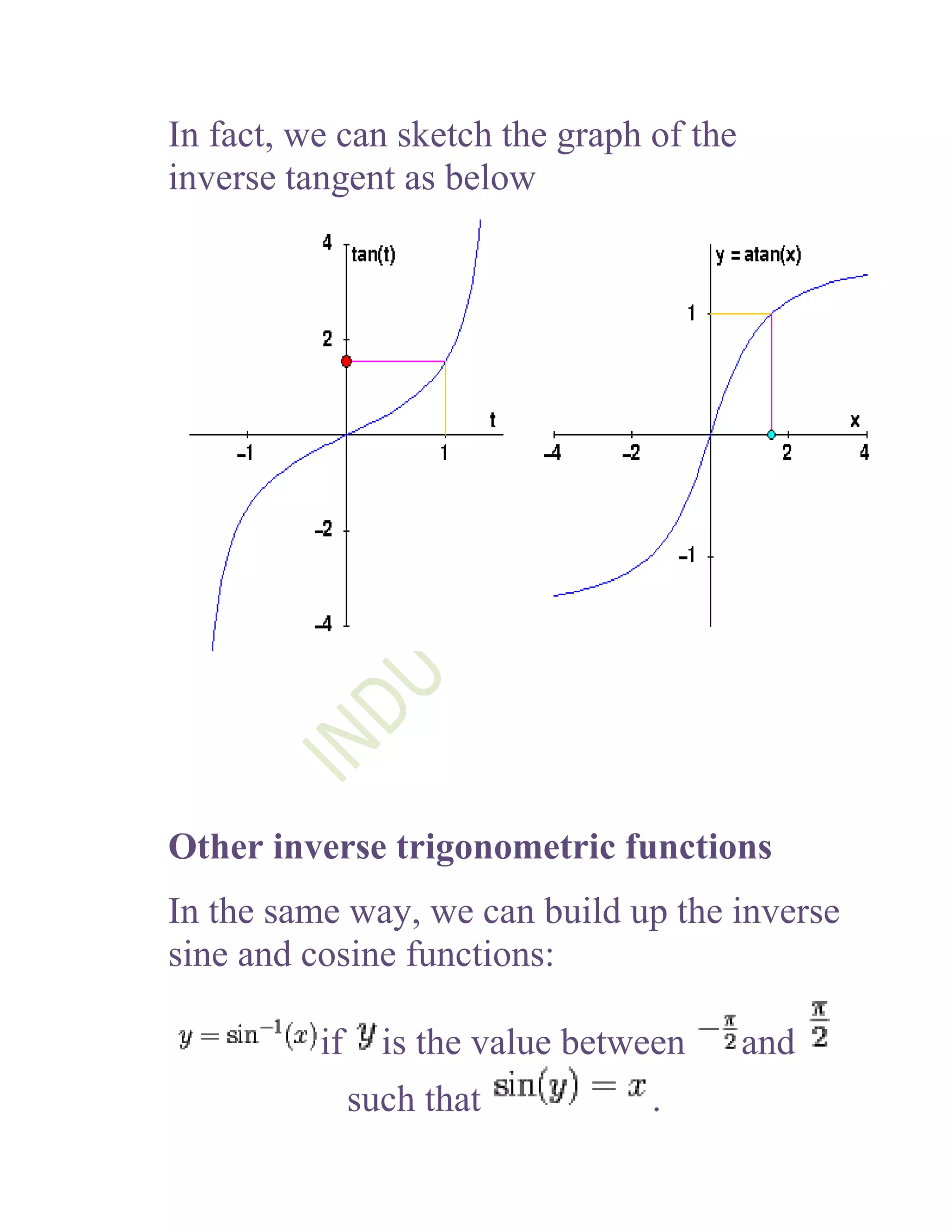
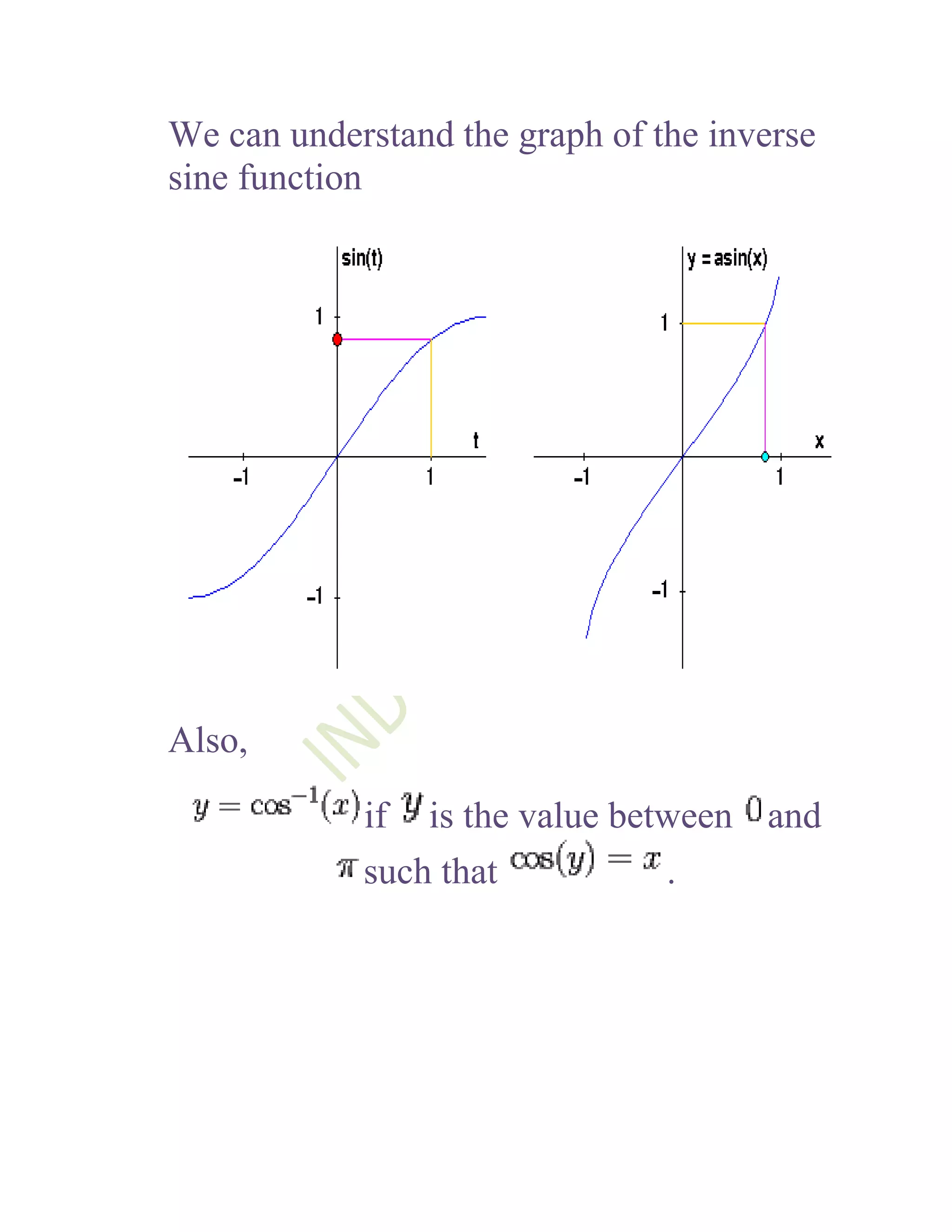
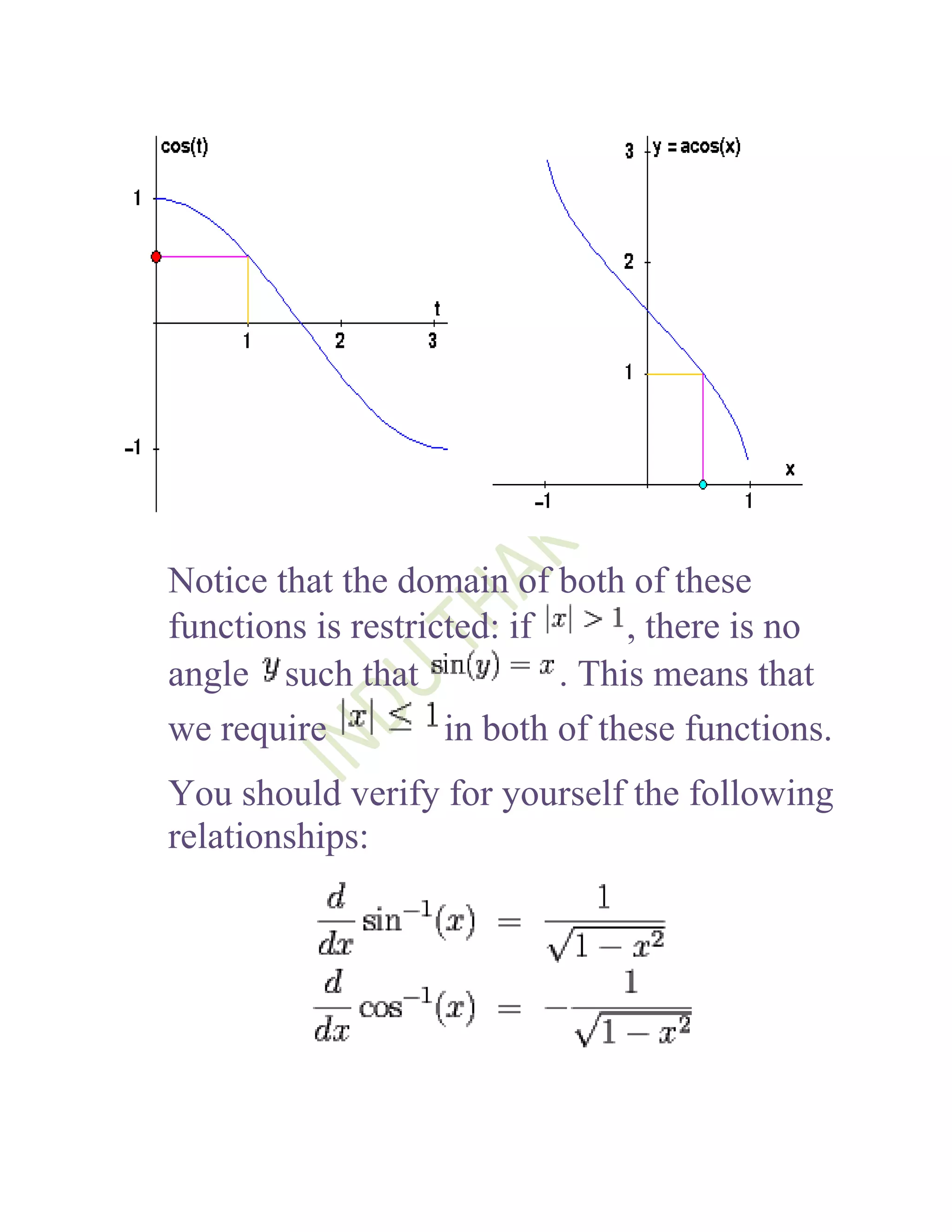
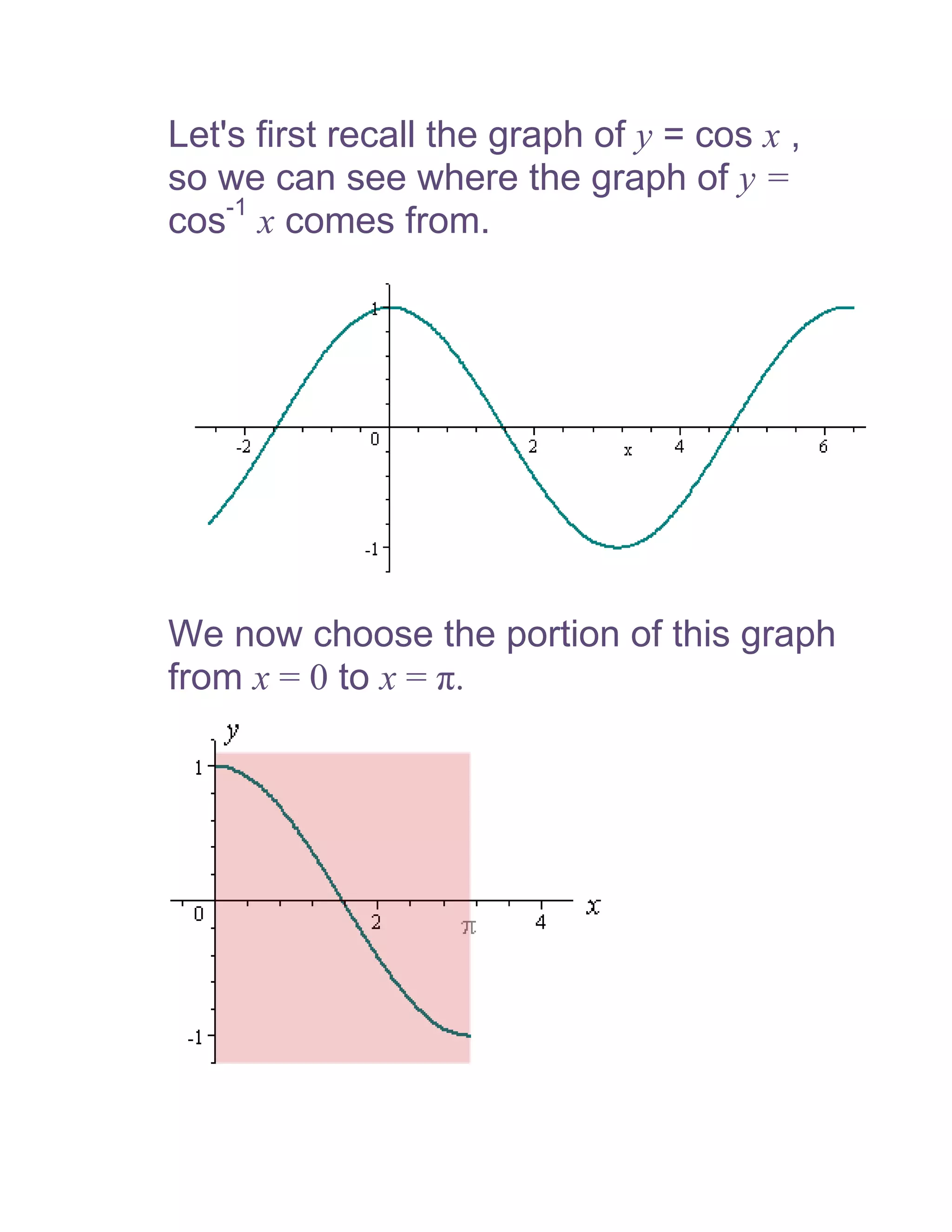
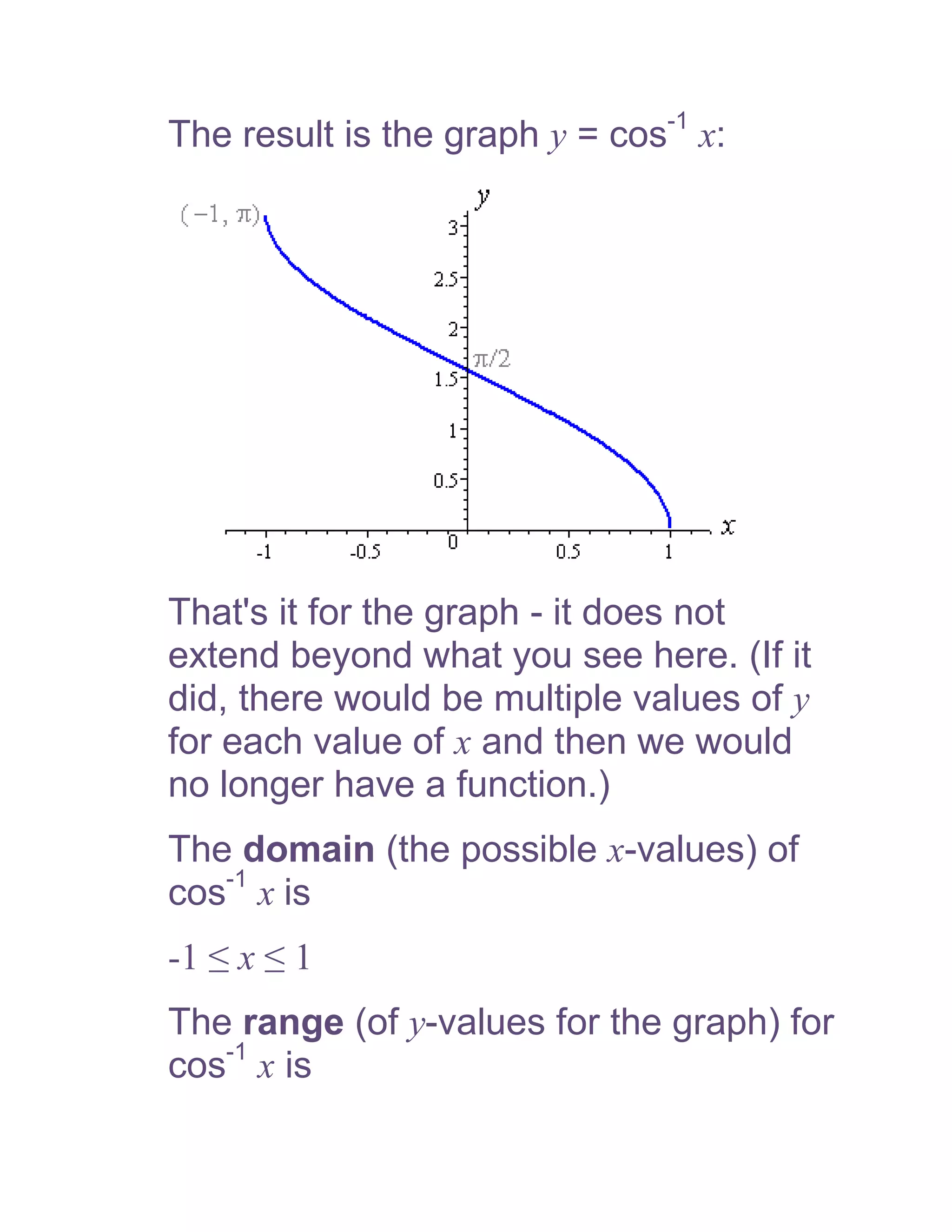
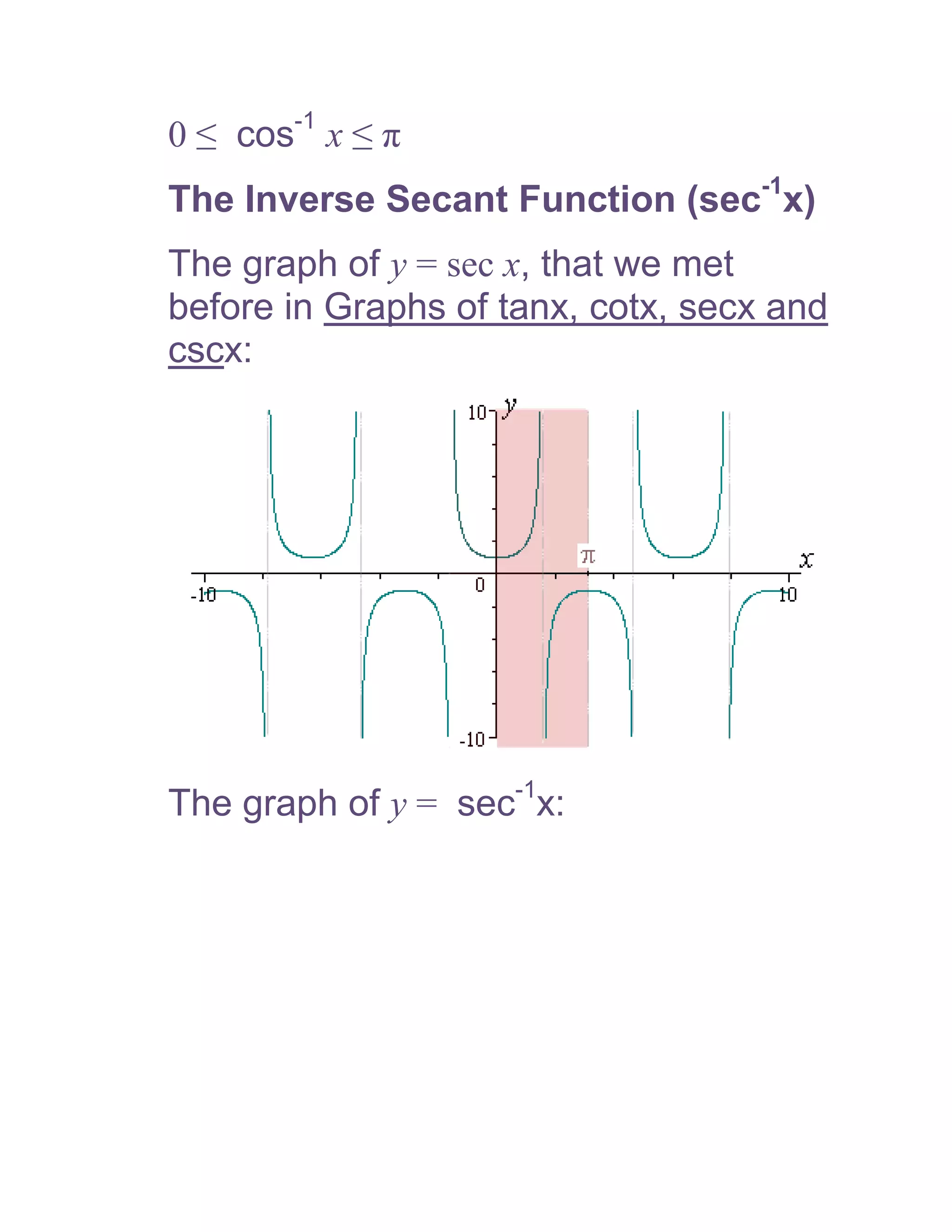
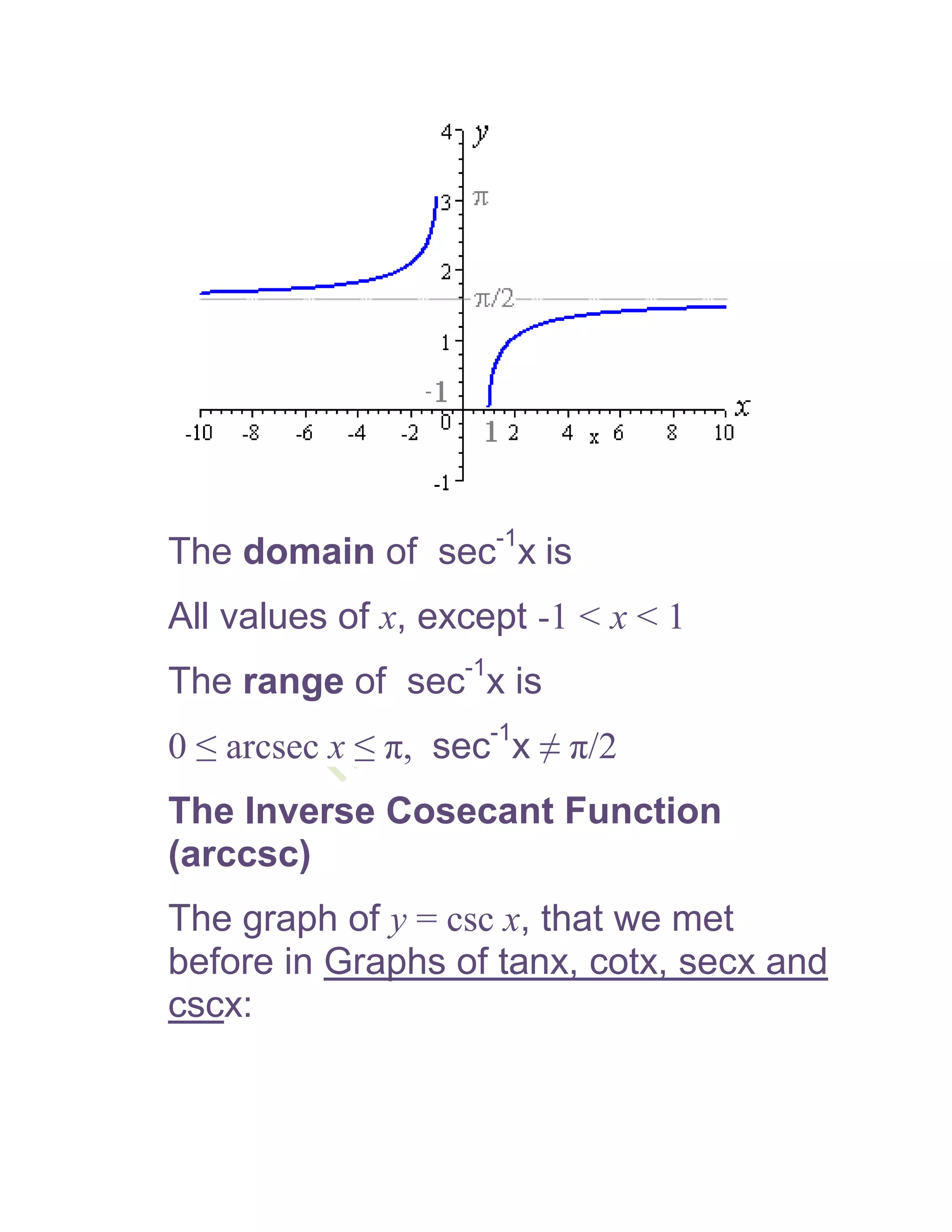
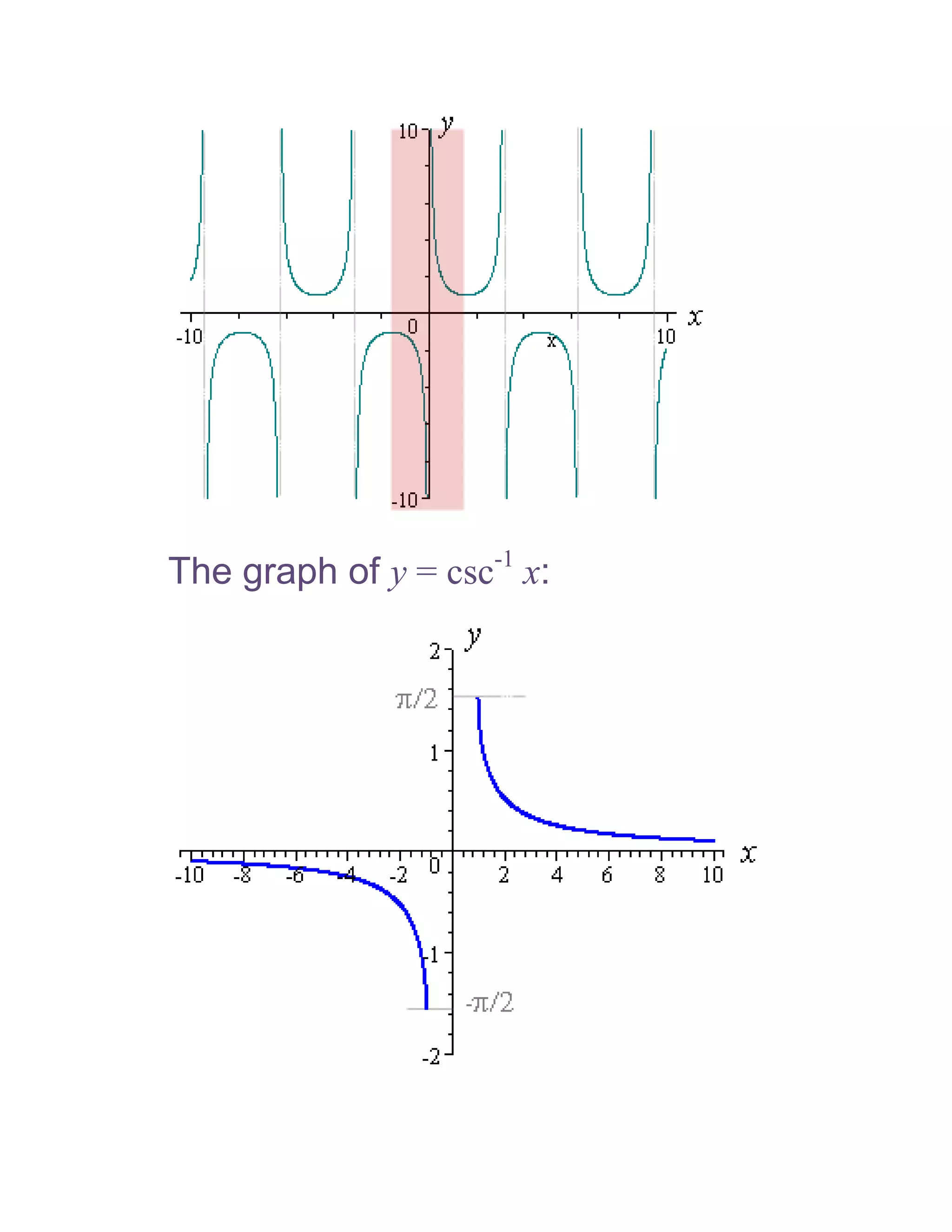
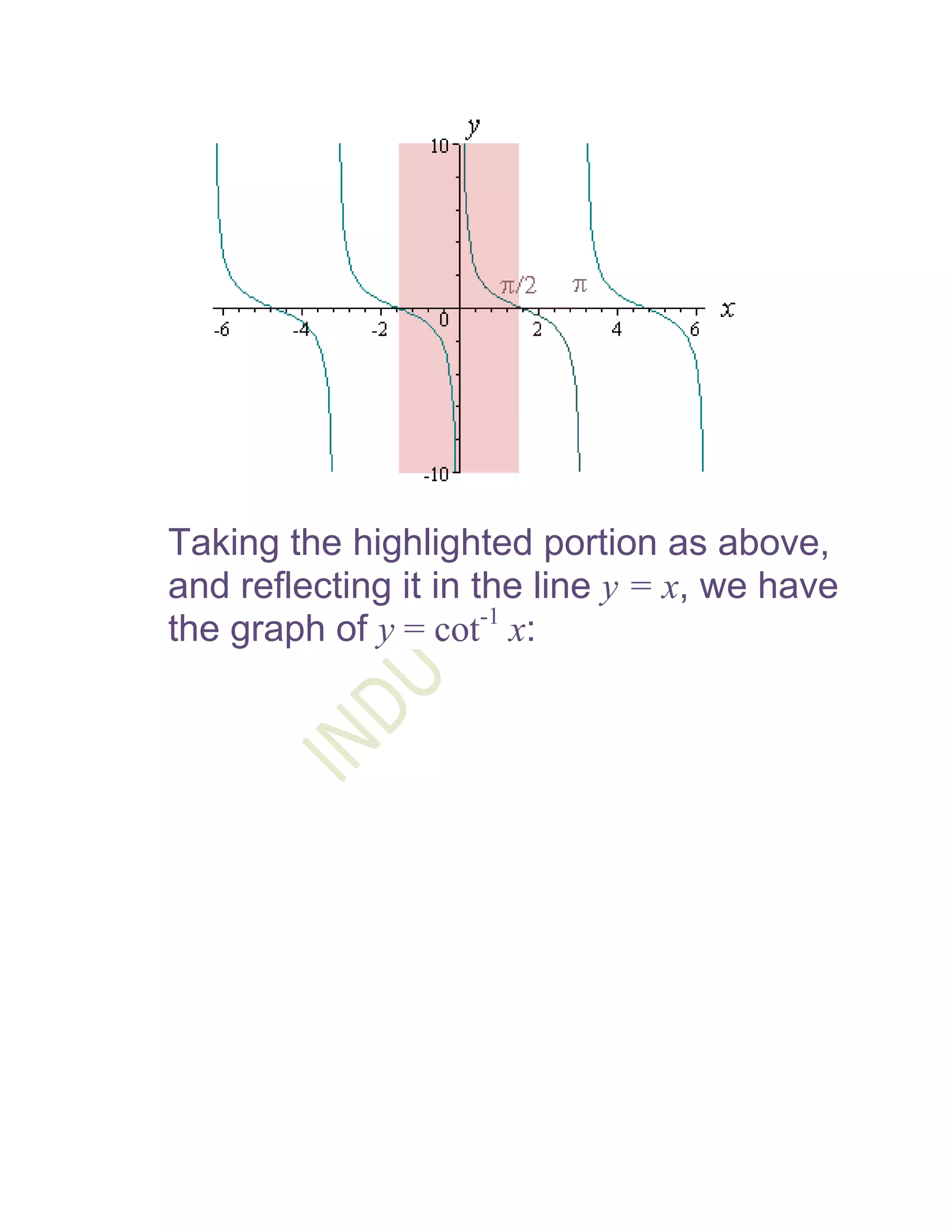
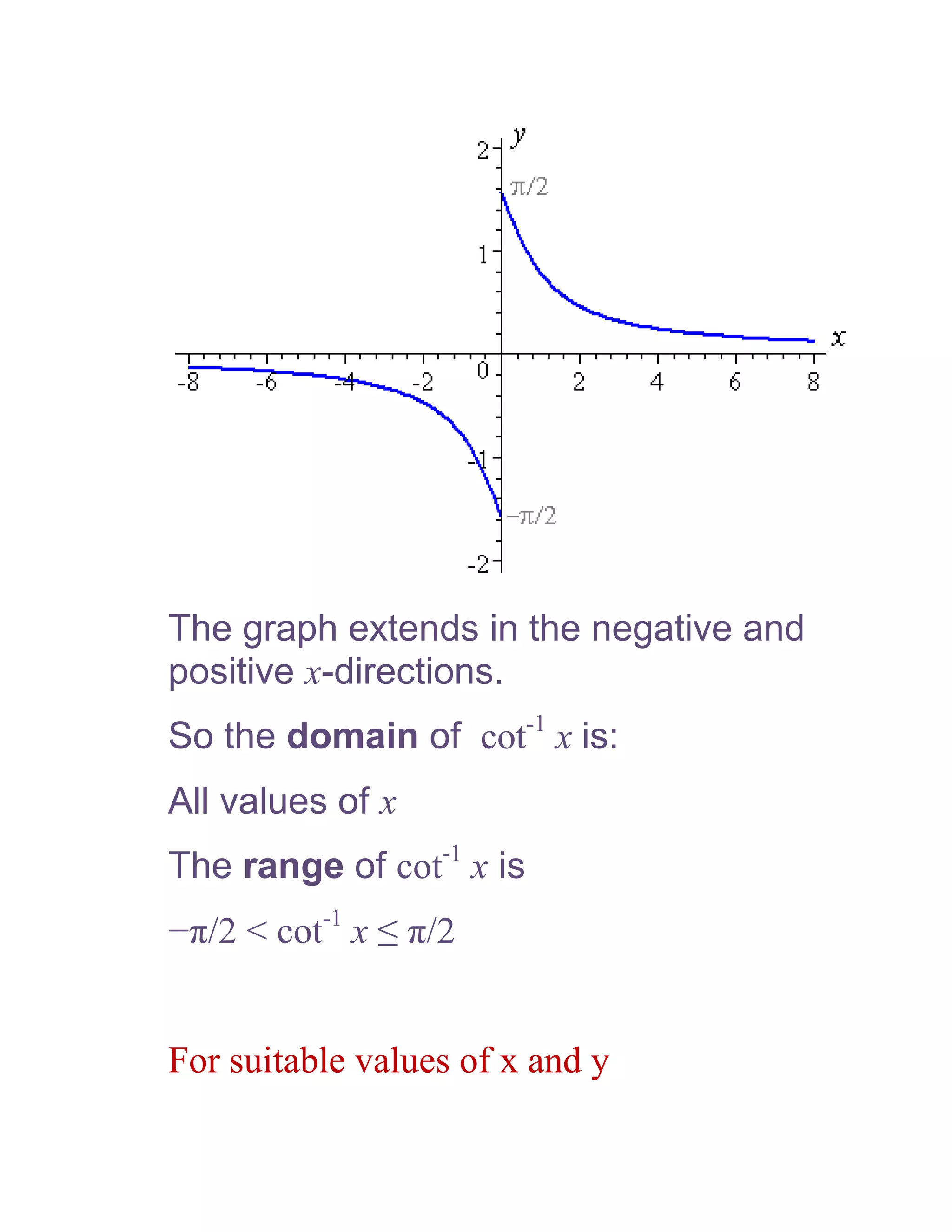
1) The document defines and discusses the domains and ranges of inverse trigonometric functions such as sin-1x, cos-1x, and tan-1x. 2) The inverse functions are defined based on reflecting portions of the original trigonometric functions over the line y=x. 3) The domains and ranges of the inverse functions are restricted to ensure each inverse function is a single-valued function.

1. Inverse Trigonometric Functions
Table of domain and range of inverse
trigonometric function
Inverse-forward identities are
Forward-inverse identities are

2. Relation between inverse functions:

4. Example -- "the angle
."
1. Evaluate sin -1 2 whose sine is 2

5. Solution. is the sine of what angle?
2
π
= sin
2 4
That is,
π
Sin-1 = .
2 4
The range of y = arcsin x=sin-1x
is not the only
π . is the sine of
But angle whose sine
4 2 2 every 1st and
is
2nd quadrant angle whose corresponding π
acute angle is 4
3π
sin = .
4 2
π
sin ( + 2π) = .
4

6. 2
And so on.
For the function y = sin-1x to be single-
valued, then, we must restrict the values of y.
How will we do that? We will restrict them to
those angles that have the smallest absolute
value.
In that same way, we will restrict the range of
each inverse trigonometric function. (Topic 3
of Precalculus.)
is the angle of
π smallest
.
4 absolute value 2
whose sine is
Example
2. Evaluate sin- )
1
(− 2
Solution. Angles whose sines are negative fall
in the 3rd and 4th quadrants. The angle of
smallest absolute value is in the 4th

7. π
quadrant. It is the angle − .
4
-1 π
sin (− )=− .
2 4
For angles whose sine is negative, we always
choose a 4th quadrant angle. In fact,
sin-1 (−x) = − sin-1x
sin-1(−½) = − sin-1½
π
=− .
6
*
To see that sin-1 (−x) = − sin-1x, look here:

8. = θ.
= −θ.
Here, then, is the range of the function y =
sin-1x

9. To restrict the range of arcsin x
is equivalent to restricting the
domain of sin x to those same
values. This will be the case
with all the restricted ranges
that follow.
.)
Problem 2. Evaluate the following in
radians.
a) sin-1 0 = 0.

10. b) sin-1 1 = π/2.
c) sin-1 (−1) = −π/2.
π/3.
−π/3.
−π/6.
The range of y = tan-1 x
Similarly, we must restrict the range of y =
tan-1 x. Like y = sin-1 x, y = tan-1 x has its
smallest absolute values in the 1st and 4th
quadrants.

11. For angles whose tangent is postive, we
choose a 1st quadrant angle. For angles
whose tangent is negative, we choose a 4th
quadrant angle. Like sin-1 (−x),
tan-1 (−x) = −tan -1x.

12. = −θ.
= θ.
Problem 3. Evaluate the following.
-1
π -1
π
a) tan 1 = b) tan (−1) = −
4 4

13. π π
−1
c) tan = −1
d) tan (− ) = −3
3
-1 π
e) tan 0 = 0 f) =−
6
The range of y = cos-1 x
The values of y = Cos-1 x will have their
smallest absolute values when y falls within
the 1st or 2nd quadrants.
Example 3. Evaluate
a) cos-1 ½
Solution. The radian angle whose π
(60°).
cosine is ½ is 3

14. b) cos-1 (−½)
Solution. An angle x whose cosine is
negative falls in the 2nd quadrant.
And the cosine of a 2nd quadrant angle is
the negative of the cosine of its supplement.
This implies:
An angle θ whose cosine is −x is the supplement
of the angle whose cosine is x.
cos-1 (−x) = π – cos-1 x.
Therefore,
cos-1 (−½) = π – cos-1 ½
=
2π
=
3
Problem 4. Evaluate the following.

15. a) cos-1 1 = 0 b) cos-1 (−1) = π
−1 π −1 3π
c) cos = d) cos (− )=
2 4 2 4
π 5π
e) cos-1 0 = f) =
2 6
The range of y = sec-1 x
In calculus, sin−1x, tan−1x, and cos−1x are
the most important inverse trigonometric
functions. Nevertheless, here are the ranges
that make the rest single-valued.
The Inverse Sine Function (sin-1 x)
We define the inverse sine function as

16. y = sin-1 x for
where y is the angle whose sine is x. This
means that
x = sin y
The graph of y = sin-1 x
Let's see the graph of y = sin x first and then
derive the curve of y = sin-1 x.
As we did previously , if we reflect the
indicated portion of y = sin x through the line
y = x, we obtain the graph of y = sin-1 x:

17. Once again, what you see is what you get.
The graph does not extend beyond the
indicated boundaries of x and y.
The domain (the possible x-values) of sin-1
x is
-1 ≤ x ≤ 1
The range (of y-values for the graph) for sin-
1
x is
-π/2 ≤ sin-1 x ≤ π/2
The Inverse Tangent Function (tan-1x)

18. As a reminder, here is the graph of y = tan x,
that we met before in Graphs of tanx, cotx,
secx and cscx.
Reflecting this portion of the graph in the
line y = x, we obtain the graph of y = tan-1 x:

19. This time the graph does extend beyond
what you see, in both the negative and
positive directions of x.
The domain (the possible x-values) of tan-1
x is
All values of x
The range (of y-values for the graph) for
arctan x is
-π/2 < tan-1 x < π/2

20. The graph of the inverse of cosine x is
found by reflecting the graph of cos x
through the line y = x.
We now reflect every point on this portion of
the cos x curve through the line y = x.

21. The result is the graph y =cos-1 x:

22. That's it for the graph - it does not extend
beyond what you see here. (If it did, there
would be multiple values of y for each value
of x and then we would no longer have a
function.)
The domain (the possible x-values) of cos-1
x is
-1 ≤ x ≤ 1
The range (of y-values for the graph) for
cos-1 x is
0 ≤ cos-1 x ≤ π
The Inverse Tangent Function (arctan)
As a reminder, here is the graph of y = tan x,
that we met before in Graphs of tan, cot,
sec and csc.

23. Reflecting this portion of the graph in the
line y = x, we obtain the graph of y = tan-1 x :

24. This time the graph does extend beyond
what you see, in both the negative and
positive directions of x.
The domain (the possible x-values) of tan-1
x is
All values of x
The range (of y-values for the graph) for
tan-1 x is
-π/2 < tan-1 x < π/2
The Inverse Tangent Function
Let's begin by thinking about the graph of
. If we want to solve , we may draw
a horizontal line units above the axis and
choose one of the points which lies on the
intersection of the graph and the horizontal line.

25. From this demonstration, you can see that,
as you vary the horizontal line, there are
always lots of solutions. However, there is
always a unique solution between and .
For this reason, we have a well-defined
function if define the inverse tangent
function by saying
if is the value between and
such that .
This is similar to the square root function:
there are two values which satisfy but

26. we agree, by convention, that the square root
of 4 is the positive value.
Here are some famous values of the inverse
tangent function:
-1
0 0
1

27. In fact, we can sketch the graph of the
inverse tangent as below
Other inverse trigonometric functions
In the same way, we can build up the inverse
sine and cosine functions:
if is the value between and
such that .

28. We can understand the graph of the inverse
sine function
Also,
if is the value between and
such that .

29. Notice that the domain of both of these
functions is restricted: if , there is no
angle such that . This means that
we require in both of these functions.
You should verify for yourself the following
relationships:

30. Let's first recall the graph of y = cos x ,
so we can see where the graph of y =
cos-1 x comes from.
We now choose the portion of this graph
from x = 0 to x = π.

31. The result is the graph y = cos-1 x:
That's it for the graph - it does not
extend beyond what you see here. (If it
did, there would be multiple values of y
for each value of x and then we would
no longer have a function.)
The domain (the possible x-values) of
cos-1 x is
-1 ≤ x ≤ 1
The range (of y-values for the graph) for
cos-1 x is

32. 0 ≤ cos-1 x ≤ π
The Inverse Secant Function (sec-1x)
The graph of y = sec x, that we met
before in Graphs of tanx, cotx, secx and
cscx:
The graph of y = sec-1x:

33. The domain of sec-1x is
All values of x, except -1 < x < 1
The range of sec-1x is
0 ≤ arcsec x ≤ π, sec-1x ≠ π/2
The Inverse Cosecant Function
(arccsc)
The graph of y = csc x, that we met
before in Graphs of tanx, cotx, secx and
cscx:

34. The graph of y = csc-1 x:

35. The graph extends in the negative and
positive x-directions.
The domain of csc-1 x is
All values of x, except -1 < x < 1
The range of csc-1 x is
-π/2 ≤ csc-1 x ≤ π/2, csc-1 x ≠ 0
The Inverse Cotangent Function (cot-
1
)
The graph of y = cot x, that we met
before in Graphs of tanx, cotx, secx and
cscx is as follows:

36. Taking the highlighted portion as above,
and reflecting it in the line y = x, we have
the graph of y = cot-1 x:

37. The graph extends in the negative and
positive x-directions.
So the domain of cot-1 x is:
All values of x
The range of cot-1 x is
−π/2 < cot-1 x ≤ π/2
For suitable values of x and y

38. sin-1 x + sin-1 y= sin-1 (x√1-y2+ y√1-x2)
sin-1 x - sin-1 y=sin-1 (x√1-y2- y√1-x2)
cos-1 x + cos-1 y= cos-1 (xy- √1-x2√1-y2)
cos-1 x - cos-1 y= cos-1 (xy+√1-x2√1-y2)
tan-1 x + tan-1y = ; xy<1
tan-1 x – tan-1 y= ; xy>-1
2tan-1 x= = =
Trigonometry examples
Example 1:
Solve the following equation:
Suggested answer:

40. Example 2:
Prove the following equation:
Suggested answer:

41. The angles in theoretical work will be in radian measure.
Thus if
we are given a radian π for example, then we can
angle, 6 evaluate a
function of it.
Problems – Solve Inverse Trigonometric
Functions Problems:
Problem 1:
Prove that + = , x<
Solution:
Let x = tan θ , then θ = tan-1 x. we have

42. You will take R.H.S to prove the given expression
R.H.S =
= tan-1 (tan 3θ)
= 3 θ = 3 tan-1 x
= tan-1 x + 2 tan-1 x
= + = L.H.S
Hence, the given expression will be proved.
OR
We can take L.H.S. = + =
By using
tan-1 x + tan-1y = =R.H.S.
Example problem 2:
Solve tan-1 2x + tan-1 3x = π/4
Solution:
Given: tan-1 2x + tan-1 3x = π/4
Or
tan-1 ((2x + 3x)/(1 - 2x . 3x)) = π/4

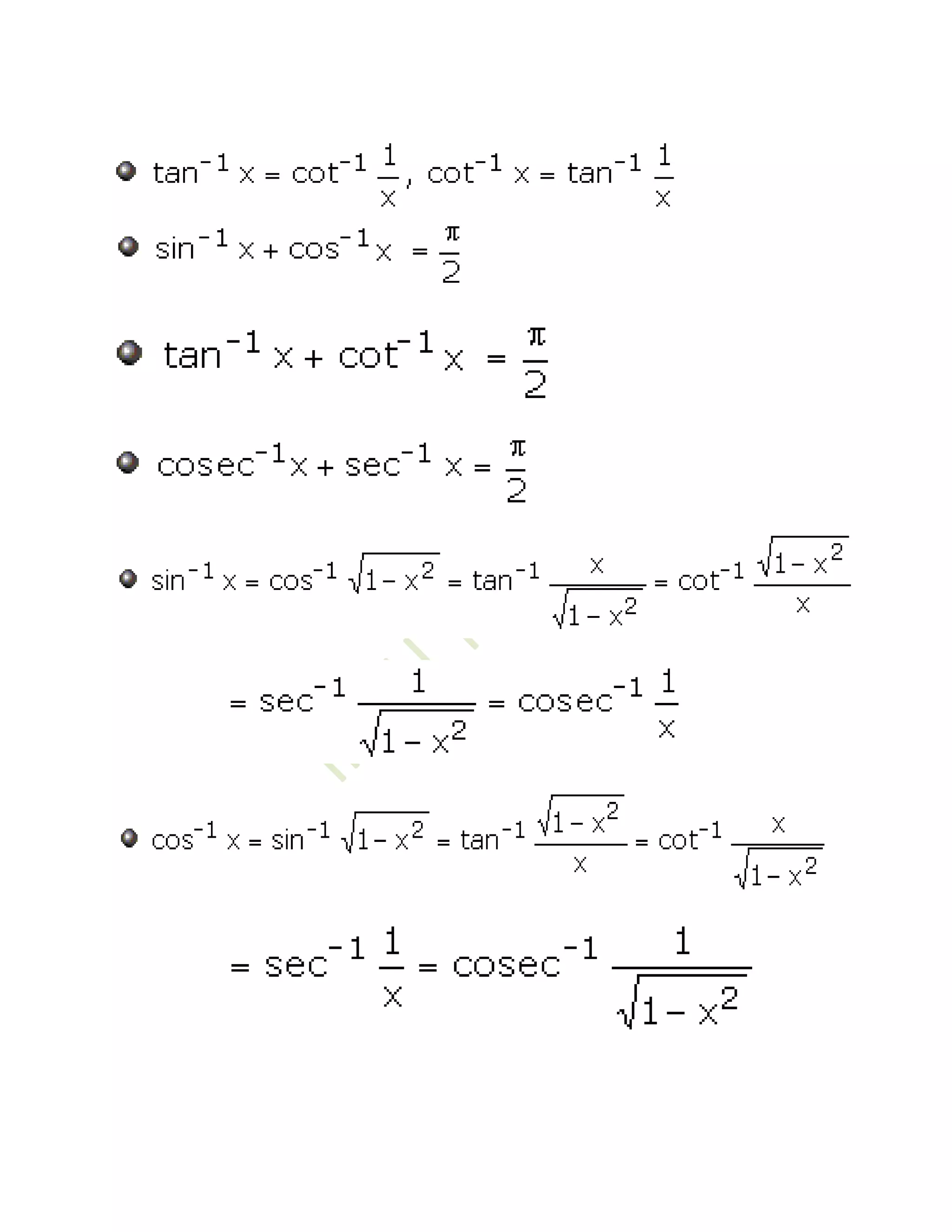
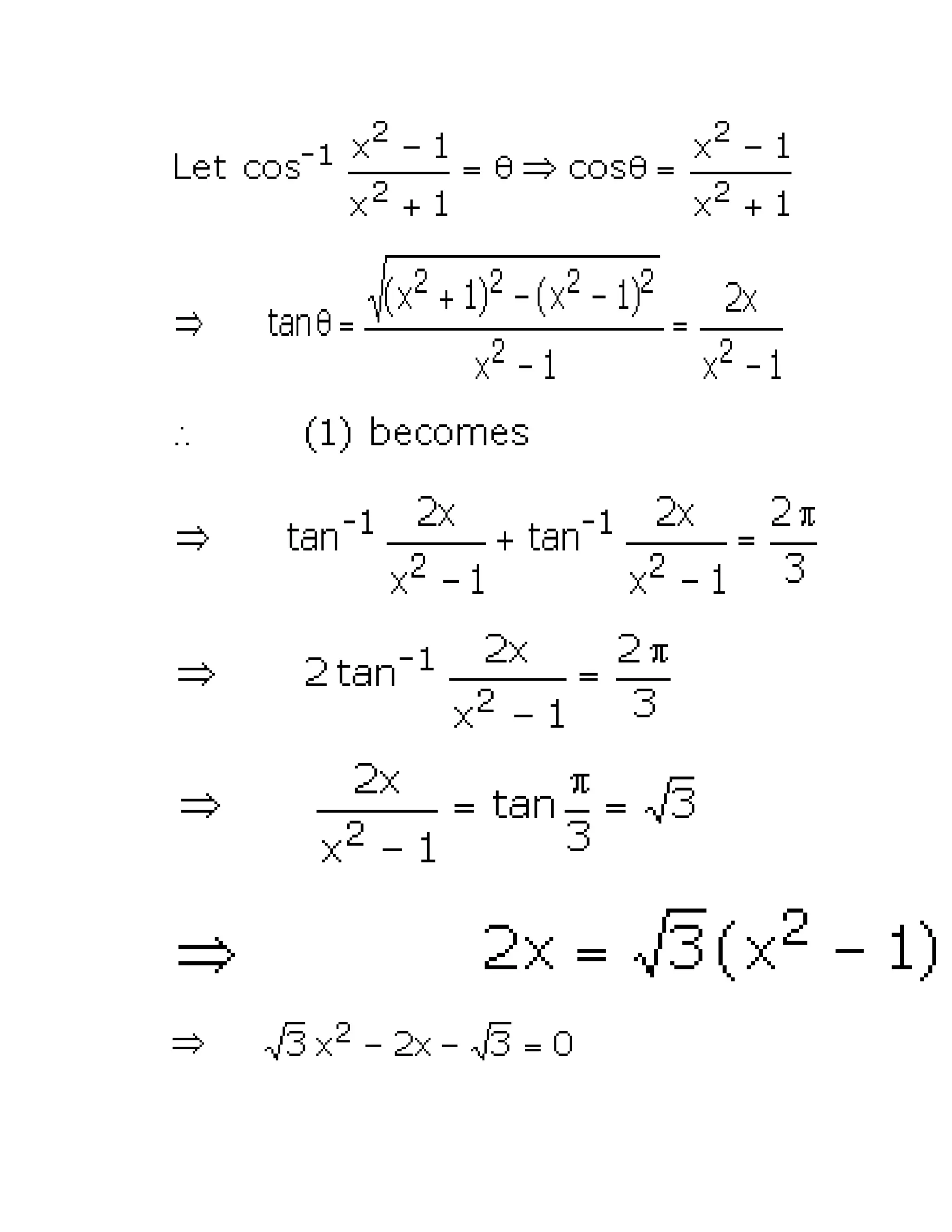
43. tan-1 ((5x)/(1 - 6x2)) = π/4
∴ (5x)/(1 - 6x2) = tan π/4 = 1
or
6x2 + 5x – 1 = 0
That means, (6x – 1)(x + 1) = 0
Which gives
x = 1/6 or x = -1
since x = -1 does not satisfy the equation ,the equation of the
L.H.S is negative, so x = 1/6 is the only solution of the given
equation.
Practice Question – Solve Inverse Trigonometric Functions
Problems:
Practice problem 1: Prove the given expresssion 3sin-1 x =
sin-1 (3x – 4x3 ), x ∈ (-1/2,1/2 )
Practice problem 2: Prove the given expression 3 cos-1 x =
cos-1 (4x3 – 3x), x ∈ (1/2, 1)
Practice problem 3: Find the value of tan-1 [ 2 cos(2 sin-1 (½)
)] [answer is п/4]
ASSIGNMENT:
Question.1 Evaluate: (i) sin-1(sin10) (ii) cos-1 (cos10) (iii)
tan-1(tan(-6))

44. Answer: (i) if –π/2 ≤x ≤π/2, then sin-1(sinx)=x but x= 10
radians does not lie between –π/2 and π/2
3π – 10 lies between –π/2 and π/2 ∴ sin-1(sin(3π-
10)) = 3π-10.
Similarly for (ii) cos-1 (cos10) = cos-1 (cos(4π-10)) =
4π-10. [10 radians does not lie between 0 and π. ∴ 0≤4π-10≤π]
For (iii) tan-1(tan(-6)) = tan-1(tan(2π-6)) = 2π-6 . { -6 radians
does not lie in [ –π/2 , π/2]}
Question.2 If x = cos-1(cos4) and y = sin-1(sin3), then which
holds? (give reason)
(i) x=y=1 (ii) x+y+1=0 (iii) x+2y=2 (iv) tan(x+y) = -tan7.
Question.3 if + = , then prove that -
cos + = sin2
[Hint: + = - ]= ⇨
cos )2 = )2
Simplify it]
Question.4 (i) sin-1x + sin-1y + sin-1z = π, then prove that
X4+y4+z4+4x2y2z2 = 2(x2y2+y2z2+z2x2)
(ii) If + + = π/2 ; prove that
xy+yz+xz = 1.
(iii) If + + = π , prove that
x+y+z = xyz.

45. [Hint: for (i) sin-1x + sin-1y = π - sin-1z ⇨ cos(sin-1x + sin-1y)
=cos( π - sin-1z)
Use cos(A-B) = cosAcosB – sinAsinB and cos(π – )= -
cos
It becomes - xy = - and simply it.
[Hint: for (ii) tan-1 x + tan-1y = ]
Question.5 Write the following functions in the simplest
form:
(i) ) (ii) ) (iii) ,-
a<x<a
[Hint: for (i) write cosx = cos2x/2 – sin2x/2 and 1+sinx
=(cosx/2 +sinx/2)2 , then use tan(A-B),
answer is π/4 – x/2 ]
[ Hint: for (ii) write cosx = sin(π/2 – x) and sinx = cos(π/2 –
x), then
use formula of 1-cos(π/2 – x)= 2sin2(π/4 – x/2) and sin(π/2 –
x) = 2 sin(π/4 – x/2) cos(π/4 – x/2)
Same method can be applied for (i) part also. Answer is π/4
+ x/2]
[ for (iii) put x=a cos , then answer will be ½ ]
Question.6 If y = ) - , prove that
siny = tan2(x/2).

46. [Hint: y = - 2 , use formula 2 =
)]
Question.7 (i) Prove that + + = π.
(ii) Prove that ) + ) +
) = 0.
[Hint: for (i) = - = , then use
formula of tan-1 x + tan-1y = ]
[Hint: write = ]
Question.8 Solve the following equations:
(i) + = .
(ii) + = .
[Hint: write = - , put = y]
[Hint: use ]
Question.9 Using principal values, evaluate ) +
). [answer is π]
Question.10 Show that tan( )= and justify why
the other value is ignored?

47. [ Hint: put =∅ ⇨ ¾ = sin2∅ = 2tan∅/(1+tan2∅), find
tan∅]
** SOME HOT QUESTIONS:
1. Which is greater tan 1 or tan-11?
2. Find the value of sin(2 ) + cos(
3. Find the value of x which satisfies the equation +
= .
4. Solve the equation: + ) = -π/2.
5. Show that tan ) = ).
6. If = - ), then find the
general value of .
ANSWERS WITH HINTS:
1. Since 1> π/4 ⇨ tan1> 1> tan-11.
2. sin(2 ) + cos( = sin2x + cosy ⇨ +
= + = .
3. + = sin( ) by using
sin(A+B)=sinA cosB + cosA sinB

48. ⇨ x + (1-x) = ∵
sin( )=
⇨ 2x – x2 = 1 ⇨ x = 0 or ½.
4. =- - ) ⇨ 6x = sin[- - )]
= -cos[ ]
= -cos[ ]=- etc.
5. 1/2(2 tan )) , use formula 2 =
and tan2x/2 = .
6. Put tan = t and use sin2 = and cos2 =
then put t/3 = T,answer is = nπ, nπ+π/4.
- = ½ ⇨ = ½
=½
= ½ (2T), then tan = 0 ,1.
.