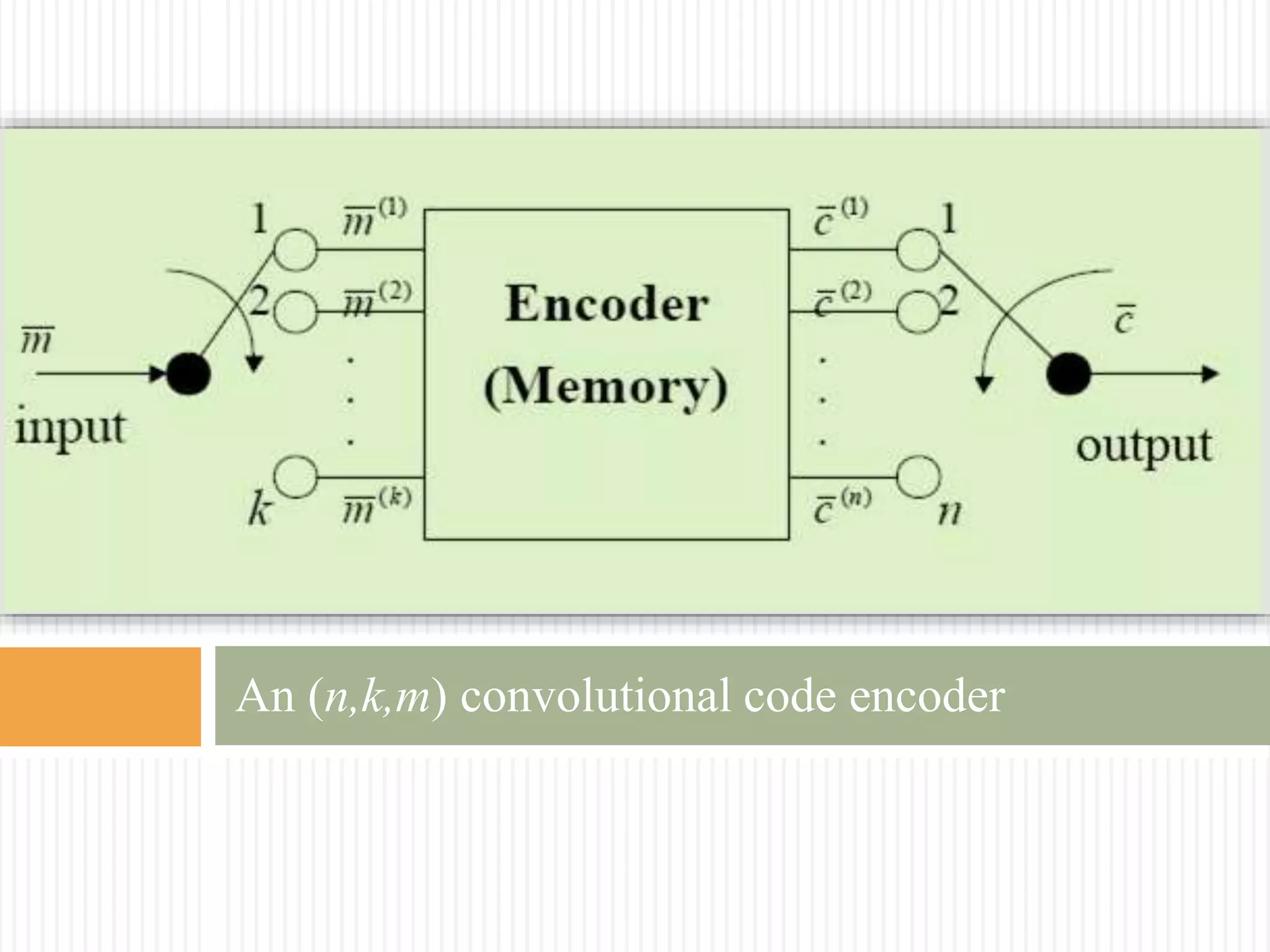
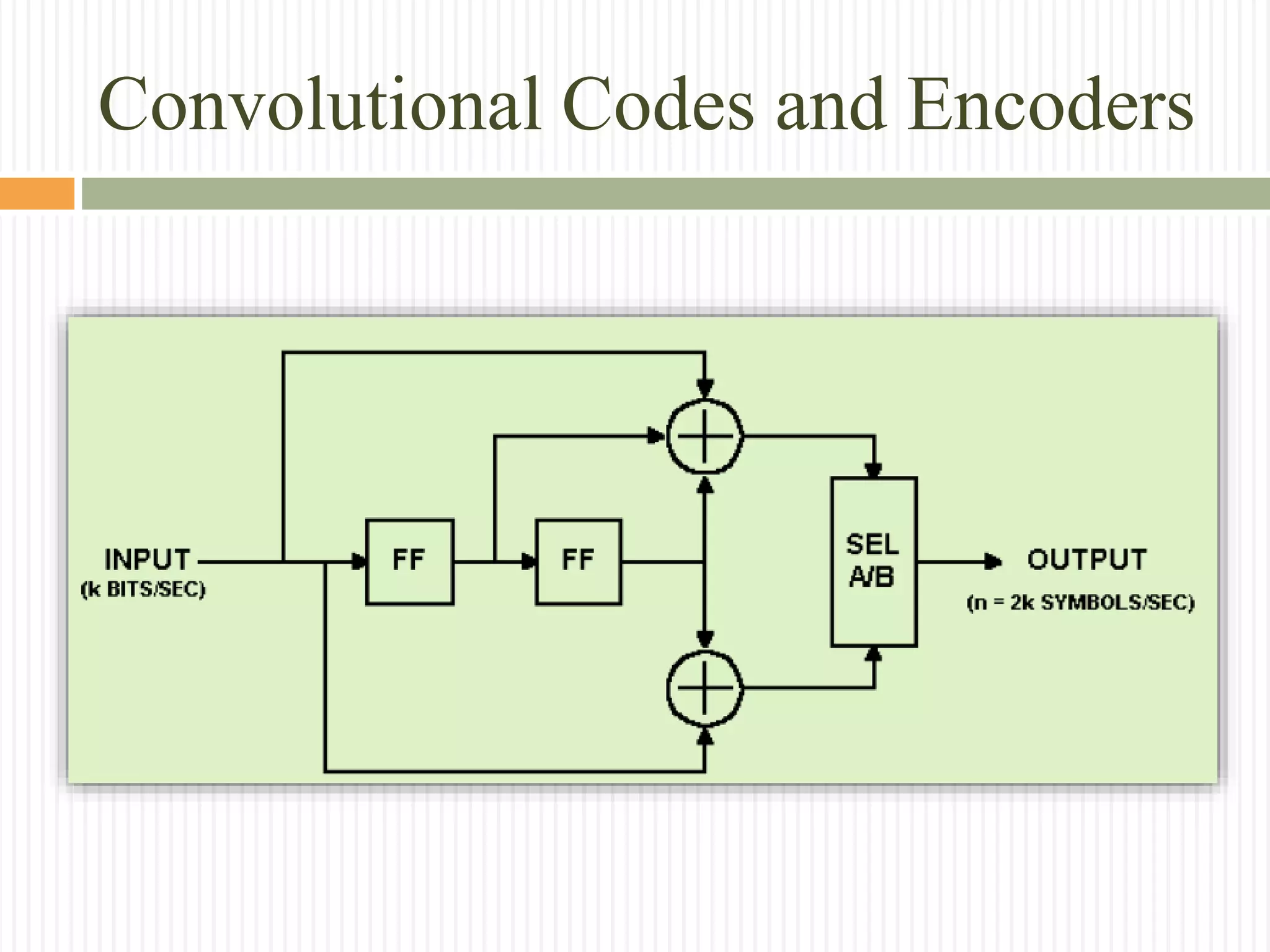
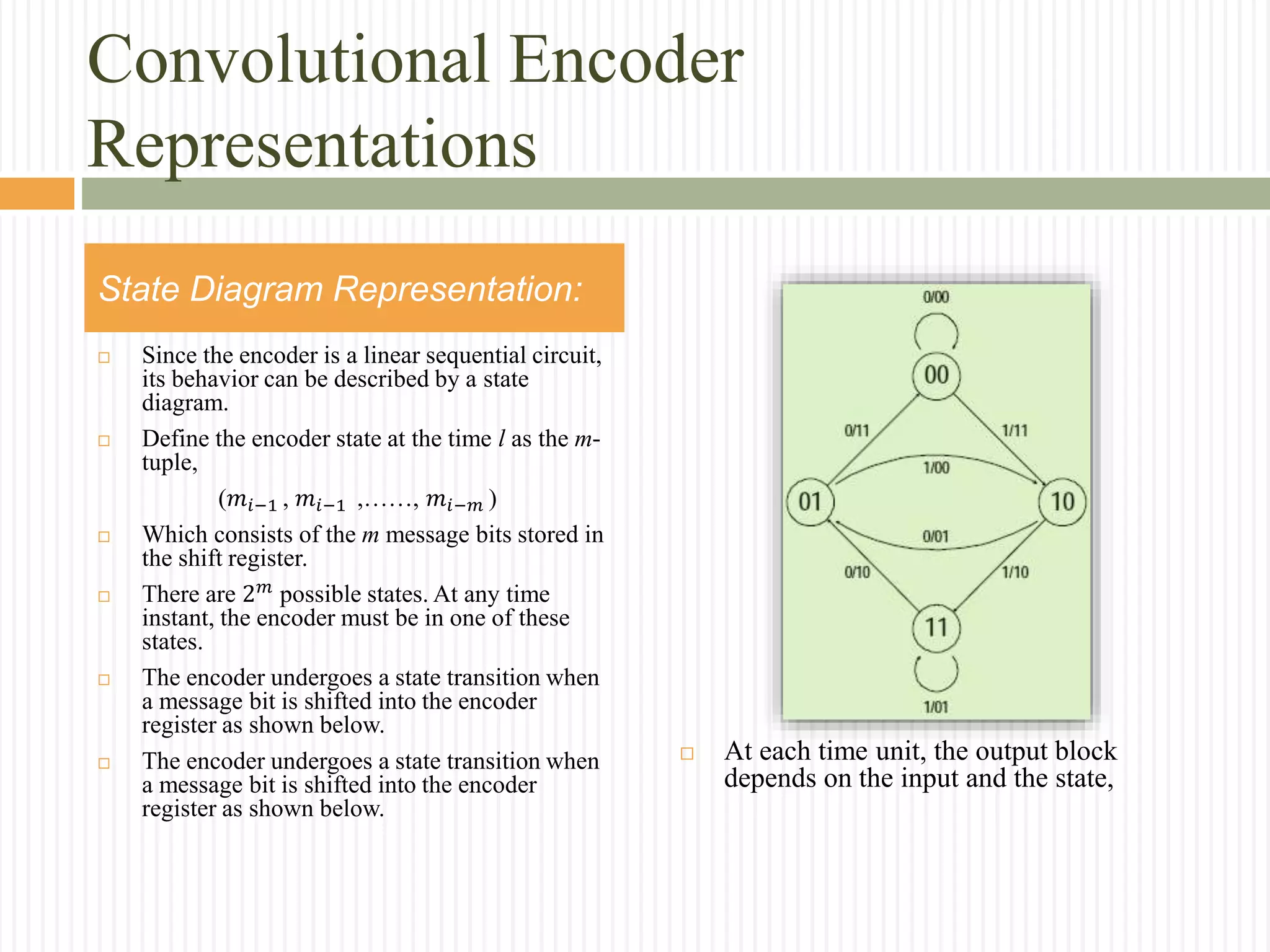
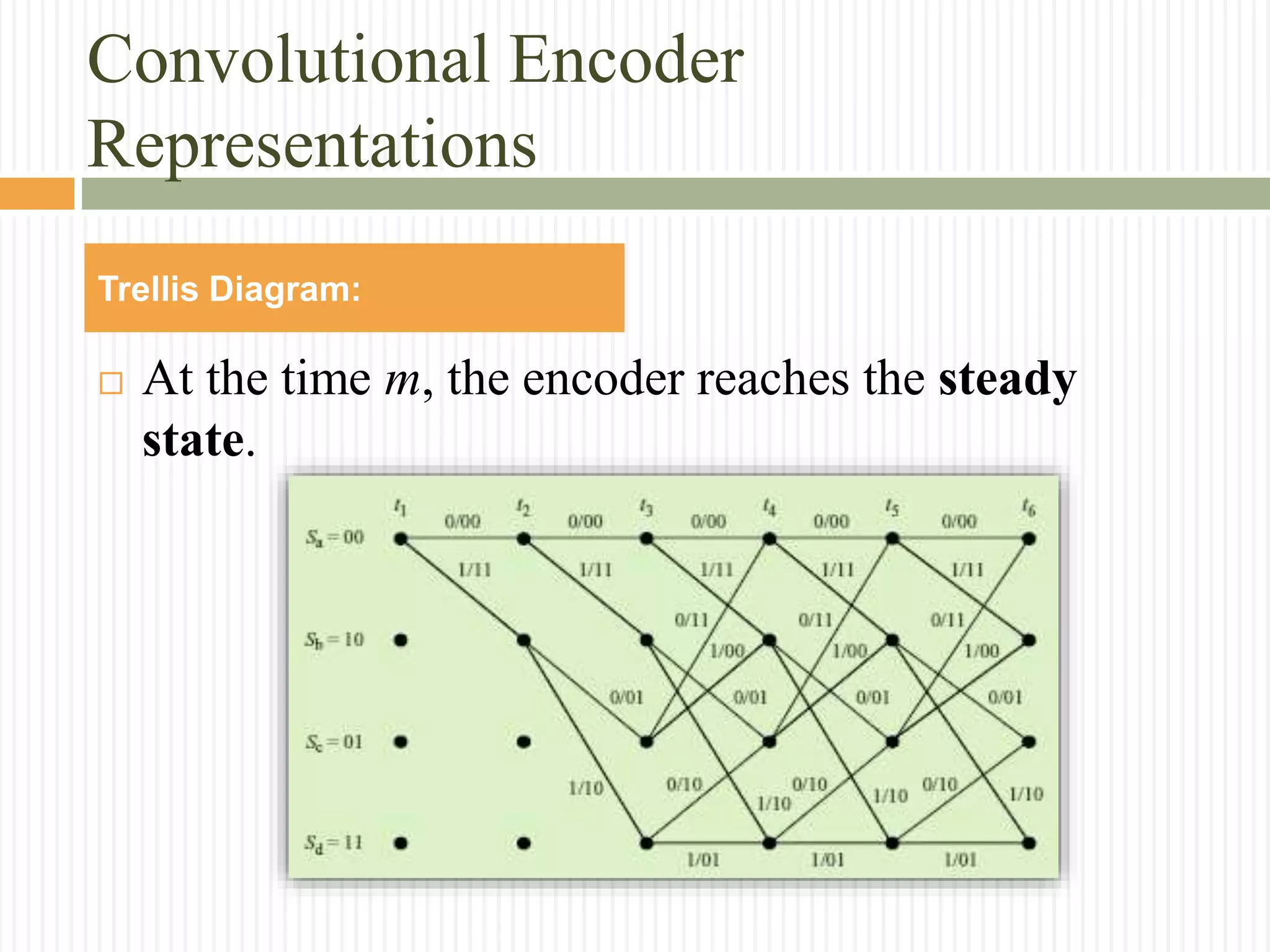
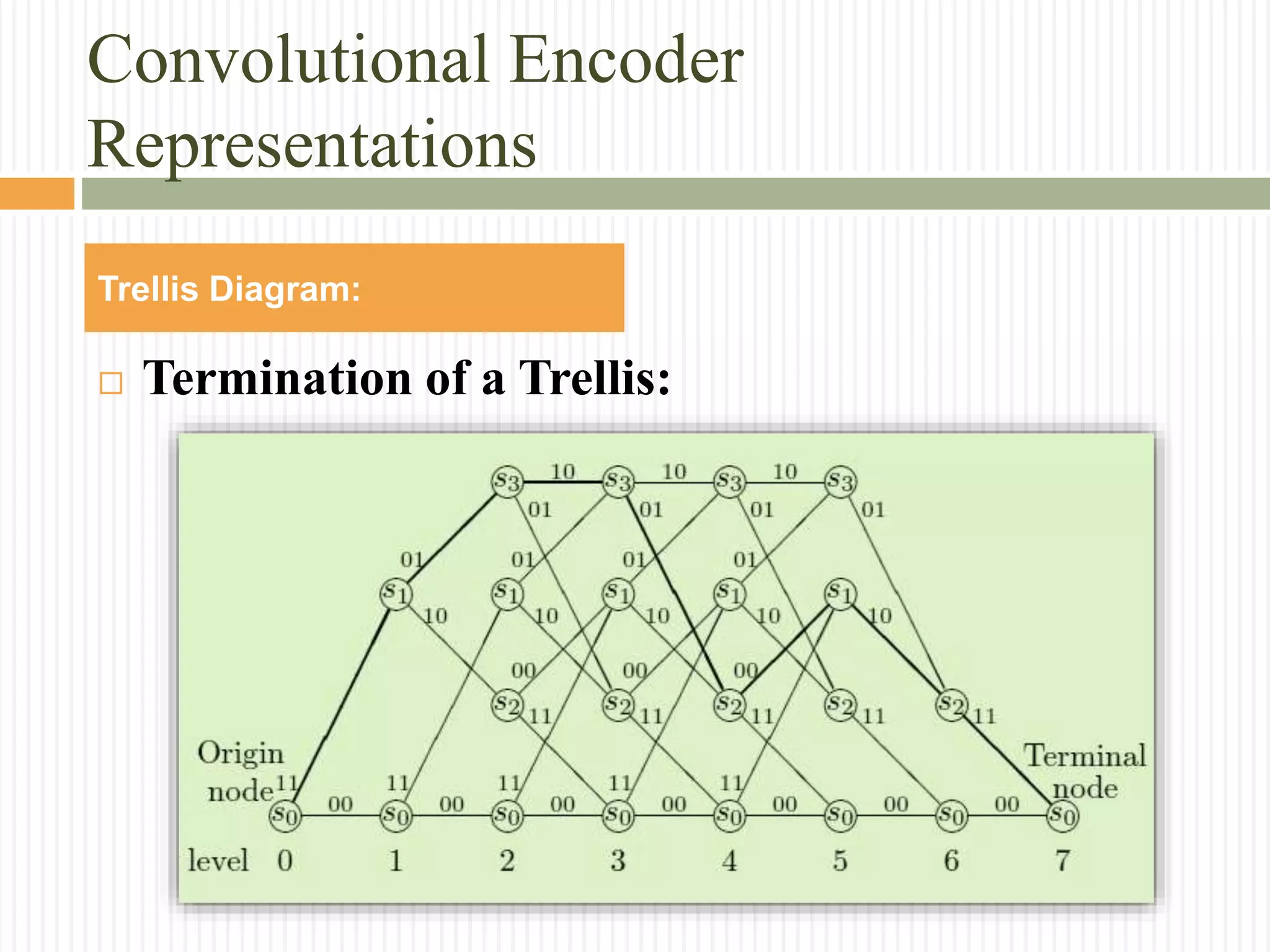
The document provides an extensive overview of convolutional codes, including their structure, encoding process, and representations in various domains. Key topics covered include the definition of convolutional codes, their encoder mechanisms, and the mathematical foundations for decoding, such as the Viterbi algorithm. Additionally, the document discusses the importance of parameters like memory order, code rate, and minimum free distance in the context of practical applications and advantages of convolutional codes.












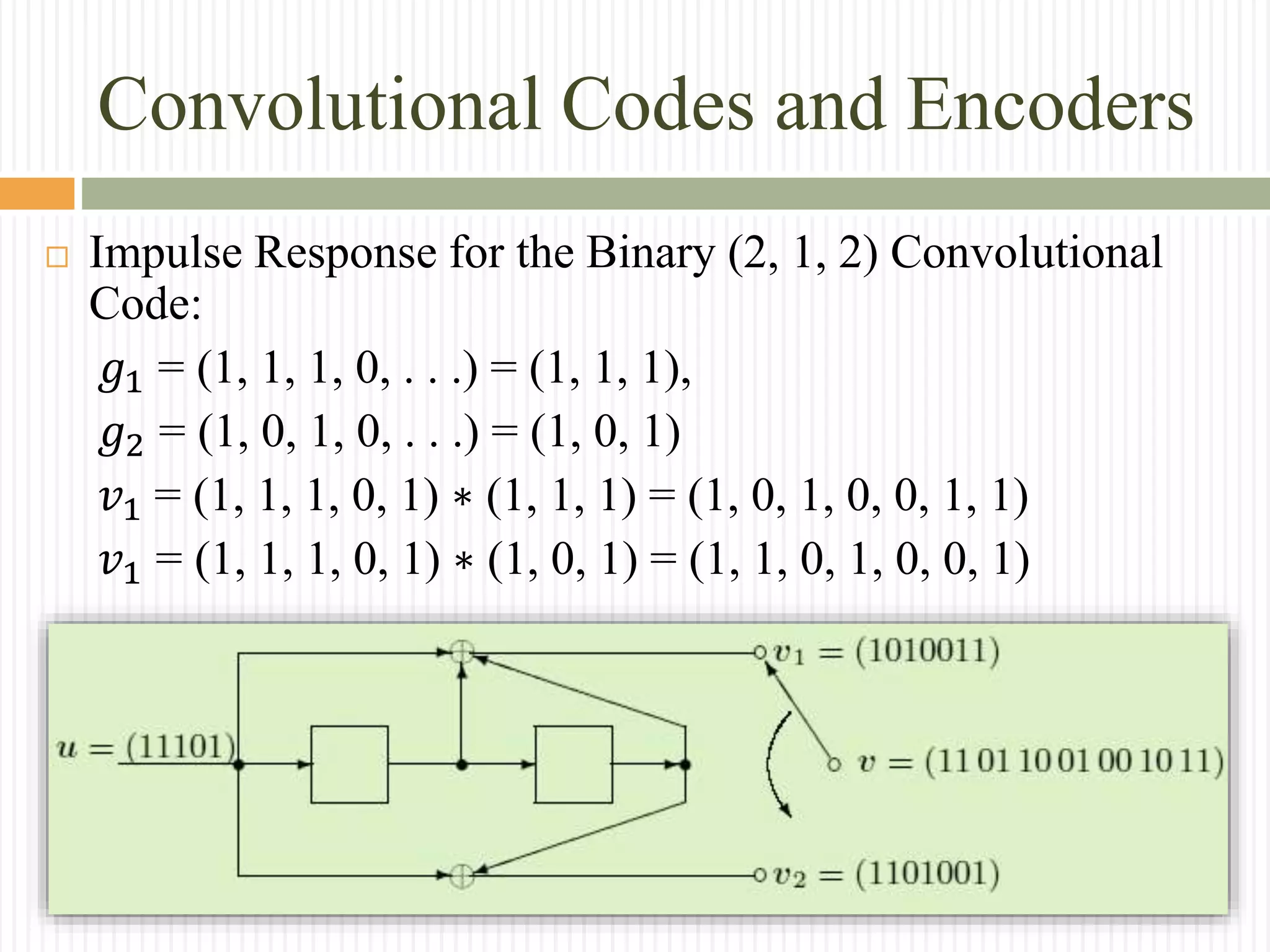



![Convolutional Codes and Encoders
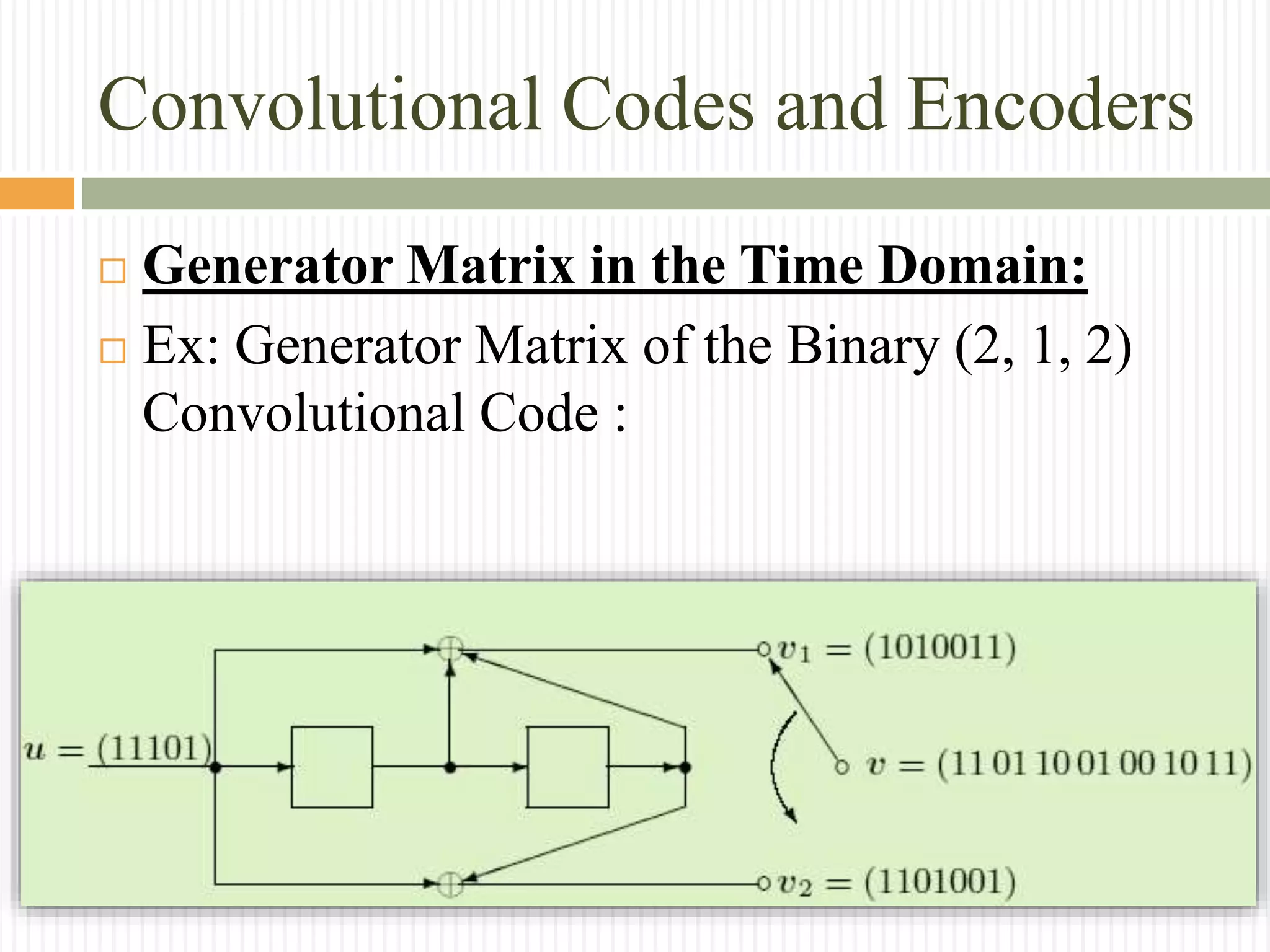
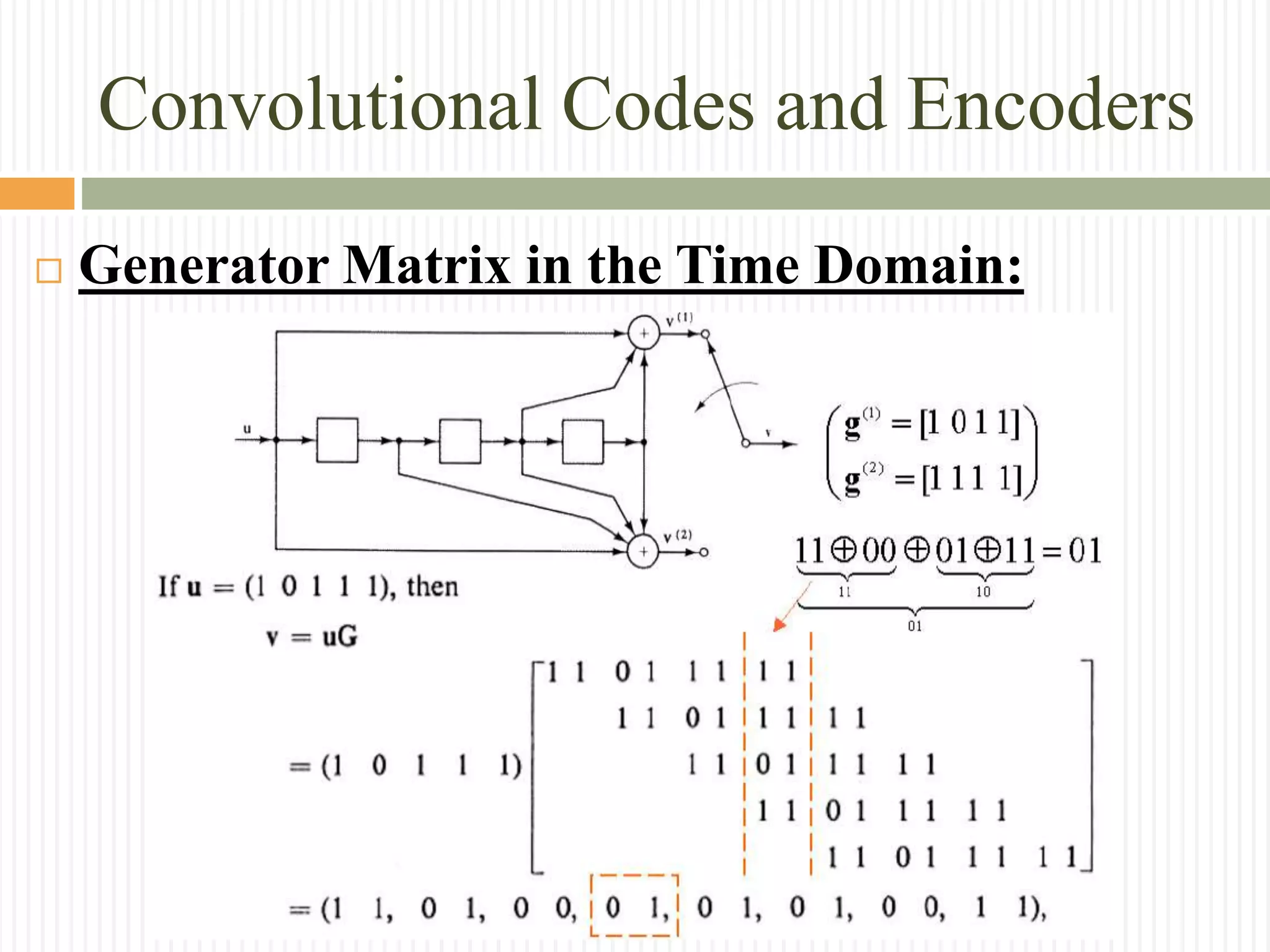
Generator Matrix in the Time Domain:
With the k × n submatrices :
𝐺𝑙=
𝑔1,𝑙
(1)
𝑔2,𝑙
(1)
⋯ ⋯
𝑔1,𝑙
(2)
𝑔2,𝑙
(2)
⋯ ⋯
⋮ ⋮
𝑔 𝑛,𝑙
(1)
𝑔 𝑛,𝑙
(2)
⋮
𝑔1,𝑙
(𝑘)
𝑔2,𝑙
(𝑘)
⋯ ⋯𝑔 𝑛,𝑙
(𝑘)
The element 𝑔𝑗,𝑙
(𝑖)
, for i ∈ [1, k] and j ∈ [1, n], are the
impulse response of the i-th input with respect to j-th output](https://image.slidesharecdn.com/convolutionalcodes-160225232604/75/Convolutional-codes-19-2048.jpg)




![Description in the D-Transform
Domain
Ex: (2,1,2) convolutional code encoder :
G(1)(D) = 1 + 𝐷 + 𝐷2
G(2)(D) = 1 + 𝐷2
G(D) = [1 + 𝐷 + 𝐷2
, 1 + 𝐷2
]
U(D) = 1 + 𝐷 + 𝐷2
+ 𝐷4](https://image.slidesharecdn.com/convolutionalcodes-160225232604/75/Convolutional-codes-26-2048.jpg)









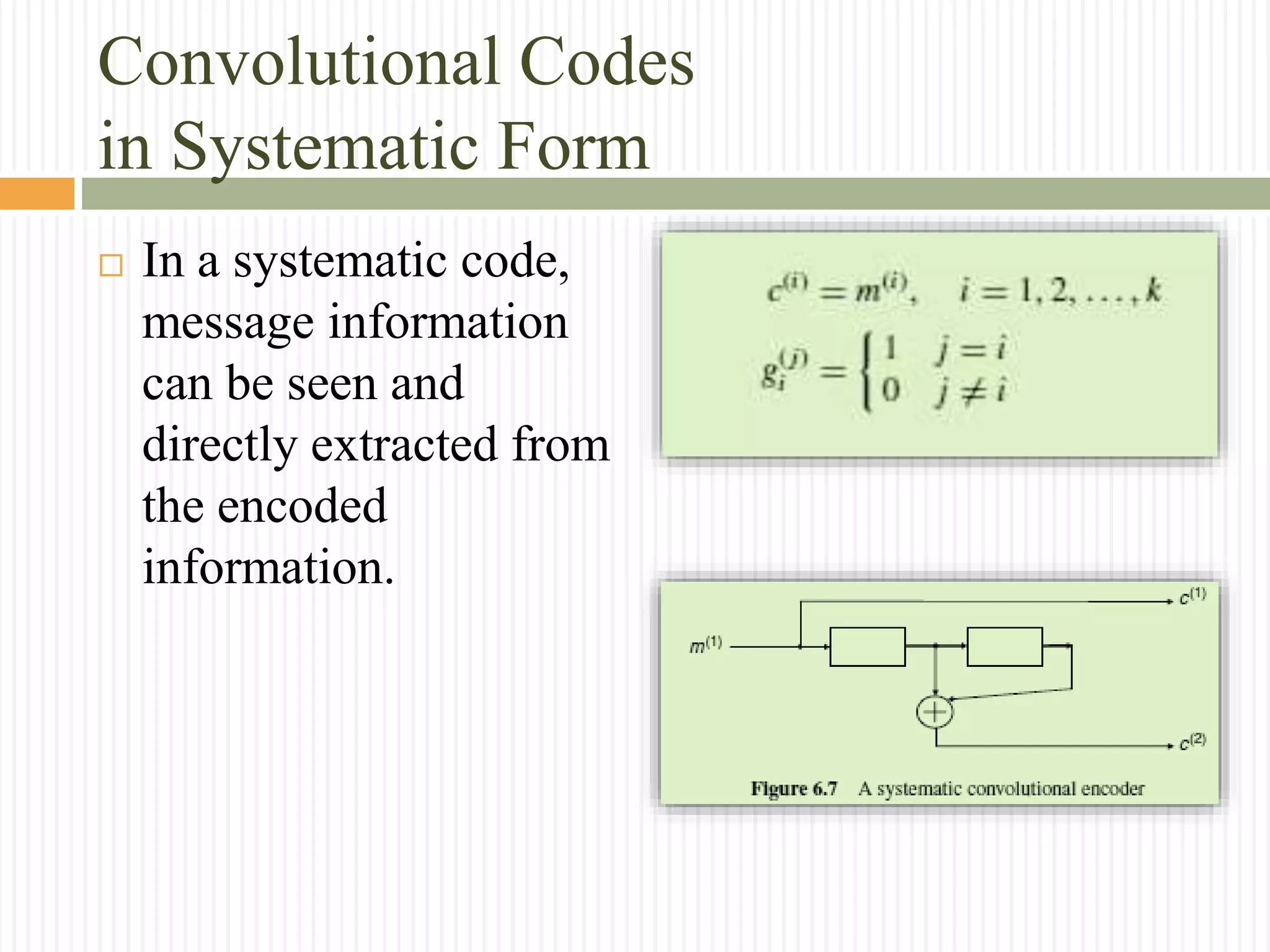
![Convolutional Codes
in Systematic Form
Example : Determine the transfer function of the systematic
convolutional code as shown in the below Figure , and then
obtain the code sequence for the input sequence m =
(1101).
Ans:
The transfer function in this case is:
G(𝐷 ) = [ 1 𝐷 + 𝐷2
]](https://image.slidesharecdn.com/convolutionalcodes-160225232604/75/Convolutional-codes-40-2048.jpg)






























