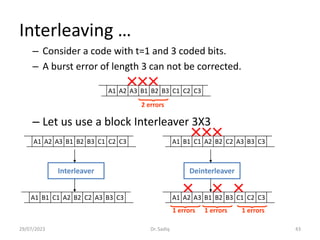
This document discusses channel coding techniques for digital communication systems. It describes two major classes of channel coding: 1) waveform coding, which transforms waveforms to make them more robust to noise and interference, and 2) structured sequence coding, which adds redundancy to sequences to enable error detection and correction. Convolutional coding is discussed in detail, including how convolutional encoders work, representations using generator polynomials and state diagrams, encoding and decoding using trellis diagrams, and the Viterbi algorithm for maximum likelihood decoding. The concept of free distance is also introduced as a way to evaluate the minimum distance between codewords in convolutional codes.

1. Digital Communication
Dr. Sadiq
29/07/2023 Dr. Sadiq 1

2. Channel Coding: Revist
29/07/2023 Dr. Sadiq 2

3. Channel Coding: Revisit
• Class of signal transformations designed to
improve communication performance by
enabling the transmitted signals to better
withstand channel distortions such as noise,
interference, and fading
• Channel coding can be divided into two
major classes:
1. Waveform coding by signal design
2. Structured sequences by adding redundancy
29/07/2023 Dr. Sadiq 3

4. Waveform coding: Concept Revisit
• deals with transforming waveform into “better
waveform” robust to channel distortion hence
improving detector performance.
• Examples:
Antipodal signaling
Orthogonal signaling
Bi-orthogonal signaling
M-ary signaling
Trellis-coded modulation
29/07/2023 Dr. Sadiq 4

5. Channel Coding: Concept Revisit
• Deals with transforming sequences into
“better sequences” by adding structured
redundancy (or redundant bits).
• The redundant bits are used to detect and
correct errors hence improves overall
performance of the communication system
29/07/2023 Dr. Sadiq 5
Message Encoder Channel Decoder Message
10 101010 noise 001010 10

6. Channel Coding
Examples:
– Linear Block codes
• Hamming codes
• BCH codes
• Cyclic codes
• Reed-Solomon codes
– Non-Linear codes
• Convolutional codes
• Turbo codes(Parallel Concatenated codes)
29/07/2023 Dr. Sadiq 6

7. Channel Coding
Examples:
– Linear Block codes
• Hamming codes
• BCH codes
• Cyclic codes
• Reed-Solomon codes
– Non-Linear codes
• Convolutional codes
• Turbo codes(Parallel Concatenated codes)
29/07/2023 Dr. Sadiq 7
Previously
done
To do!

8. 29/07/2023 Dr. Sadiq 8
Block diagram of the Dig. Com. Sys:
Convolutional Coding
Information
source
Rate 1/n
Conv. encoder
Modulator
Information
sink
Rate 1/n
Conv. decoder
Demodulator

 

 

sequence
Input
2
1 ,...)
,...,
,
( i
m
m
m

m

 

 



 


 

bits)
coded
(
rd
Branch wo
1
sequence
Codeword
3
2
1 ,...)
,...,
,
,
(
n
ni
ji
i
i
i
,...,u
,...,u
u
U
U
U
U
U


 G(m)
U
,...)
ˆ
,...,
ˆ
,
ˆ
(
ˆ 2
1 i
m
m
m

m
1 2 3 i
received sequence
(Z ,Z ,Z ,...,Z ,...)

Z
Channel

9. Convolutional vs Block codes
• Convolutional encoder among most commonly used
channel codes
– Encodes information stream rather than information blocks
– does not need to segment the data stream into blocks of
fixed size
– is a machine with memory as Output (encoded bits)
depends not only on current input bits but also on past data
bits.
• This fundamental difference in approach imparts a different
nature to the design and evaluation of the code.
– Block codes are based on algebraic/combinatorial
techniques.
– Convolutional codes are based on construction techniques.
• Decoding most often based on the Viterbi Algorithm
29/07/2023 Dr. Sadiq 9

10. Convolutional Codes vs Block codes
29/07/2023 Dr. Sadiq 10
• Block codes are memory less ; Convolutional codes
have memory that utilizes previous bits to encode or
decode following bits.
• Convolutional codes are specified by 𝒏, 𝒌 and
constraint length that is the maximum number of
information symbols upon which the symbol may
depend (Memory size).
• Thus they are denoted by (𝒏, 𝒌, 𝑲) , where 𝑲 is the
code memory depth
• Convolutional codes are commonly used in
applications that require relatively good
performance with low implementation cost.

11. 29/07/2023 Dr. Sadiq 11
A Rate ½ Convolutional encoder
• Convolutional encoder (rate ½, K=3)
– 3 shift-registers where the first one takes the incoming
data bit and the rest, form the memory of the
encoder.
Input data bits Output coded bits
m
1
u
2
u
First coded bit
Second coded bit
2
1,u
u
(Branch word)
1
g
2
g

12. 29/07/2023 Dr. Sadiq 12
A Rate ½ Convolutional encoder
1 0 0
1
t
1
u
2
u
1
1
2
1 u
u
0 1 0
2
t
1
u
2
u
0
1
2
1 u
u
1 0 1
3
t
1
u
2
u
0
0
2
1 u
u
0 1 0
4
t
1
u
2
u
0
1
2
1 u
u
)
101
(
m 
Time Output Output
Time
Message sequence:

13. 29/07/2023 Dr. Sadiq 13
A Rate ½ Convolutional encoder
Encoder
)
101
(
m  U (11 10 00 )
10 11

0 0 1
5
t
1
u
2
u
1
1
2
1 u
u
0 0 0
6
t
1
u
2
u
0
0
2
1 u
u
Time Output Time Output
(Branch word) (Branch word)
Reset

14. 29/07/2023 Dr. Sadiq 14
Encoder representation
Vector representation:
• We define n binary vector with 𝑲 elements (one
vector for each modulo-2 adder).
• The 𝑖-th element in each vector, is “1” if the 𝑖-th
stage in the shift register is connected to the
corresponding modulo-2 adder, and “0” otherwise.
m
1
u
2
u
2
1 u
u
)
101
(
)
111
(
2
1


g
g

15. 29/07/2023 Dr. Sadiq 15
Encoder representation
• Impulse response representation:
– The response of encoder to a single “one” bit
that goes through it.
• Example:
00 1 1
0 0 1 0
0
1
1
01 1 1
2
1 u
u
Branch word
Register
contents
11
10
00
10
11
11
10
11
1
00
00
00
0
11
10
11
1
Output
Input m
Modulo-2 sum:
00 0 0
0 0 0 0
0
0
0
00 0 0

16. 29/07/2023 Dr. Sadiq 16
Impulse response and Generator Matrix:

17. 29/07/2023 Dr. Sadiq 17
Encoder representation
• Polynomial representation:
– We define n generator polynomials, one for each modulo-
2 adder.
– Each polynomial is of degree K-1 or less and describes the
connection of the shift registers to the corresponding
modulo-2 adder.
• Example:
The output sequence is found as follows:
2
2
)
2
(
2
)
2
(
1
)
2
(
0
2
2
2
)
1
(
2
)
1
(
1
)
1
(
0
1
1
.
.
)
(
1
.
.
)
(
X
X
g
X
g
g
X
X
X
X
g
X
g
g
X











g
g
1 2
interlaced wi
U( ) m( )g ( ) m( )g ( )
th
X X X X X


18. 29/07/2023 Dr. Sadiq 18
Encoder representation
In more details:
11
10
00
10
11
)
1
,
1
(
)
0
,
1
(
)
0
,
0
(
)
0
,
1
(
)
1
,
1
(
)
(
.
0
.
0
.
0
1
)
(
)
(
.
0
1
)
(
)
(
1
)
1
)(
1
(
)
(
)
(
1
)
1
)(
1
(
)
(
)
(
4
3
2
4
3
2
2
4
3
2
1
4
2
2
2
4
3
2
2
1





























U
U
g
m
g
m
g
m
g
m
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
2
m(X) 101 1 0X X
   

19. 29/07/2023 Dr. Sadiq 19
State diagram
• A state diagram is a way to represent the
encoder.
• A state diagram contains all the states and all
possible transitions between them.
• Only two transitions initiating from a state
• Only two transitions ending up in a state

20. 29/07/2023 Dr. Sadiq 20
State diagram
Current
state
input Next
state
output
00
0 00
1 11
01
0 11
1 00
10
0 10
1 01
11
0 01
1 10
0
S
1
S
2
S
3
S
0
S
2
S
0
S
2
S
1
S
3
S
3
S
1
S
1/10
10 01
00
11
0
S
1
S
2
S
3
S
1/11
1/00
1/01
0/11
0/00
0/01
0/10
Input
Output
(Branch word)

21. An Example – (rate=1/2 with K=2)
29/07/2023 Dr. Sadiq 21

22. State Diagram: an Example
29/07/2023 Dr. Sadiq 22

23. 29/07/2023 Dr. Sadiq 23
Trellis Diagram
• Trellis diagram is an extension of the state diagram
that shows the passage of time.
– Example of a section of trellis for the rate ½ code
Time
i
t 1

i
t
State
00
0 
S
01
1 
S
10
2 
S
11
3 
S
0/00
1/10
0/11
0/10
0/01
1/11
1/01
1/00

24. Encoding Process using: Trellis
29/07/2023 Dr. Sadiq 24
00
01
10
11

25. Encoding Process using: Trellis
29/07/2023 Dr. Sadiq 25
00
01
10
11

26. 29/07/2023 Dr. Sadiq 26
Soft and hard decision decoding …
• ML soft-decisions decoding rule:
– Choose the path in the trellis with minimum
Euclidean distance from the received sequence
• ML hard-decisions decoding rule:
– Choose the path in the trellis with minimum
Hamming distance from the received sequence

27. 29/07/2023 Dr. Sadiq 27
The Viterbi algorithm
• The Viterbi algorithm performs Maximum
likelihood decoding.
• It finds a path through trellis with the largest
metric (maximum correlation or minimum
distance).
– At each step in the trellis, it compares the partial metric
of all paths entering each state, and keeps only the
path with the largest metric, called the survivor,
together with its metric.

28. 29/07/2023 Dr. Sadiq 28
The Viterbi algorithm
Basic concept
1. Generate the code trellis at the decoder
2. The decoder penetrates through the code trellis
level by level in search for the transmitted code
sequence
3. At each level of the trellis, the decoder computes
and compares the metrics of all the partial paths
entering a node
4. The decoder stores the partial path with the larger
metric and eliminates all the other partial paths.
The stored partial path is called the survivor

29. Viterbi Decoding Algorithm
29/07/2023 Dr. Sadiq 29
• Trellis diagram – expanded encoder diagram
• Viterbi code – error correction algorithm
– Compares received sequence with all possible
transmitted sequences
– Algorithm chooses path through trellis whose
coded sequence differs from received sequence in
the fewest number of places
– Once a valid path is selected as the correct path,
the decoder can recover the input data bits from
the output code bits

30. VITERBI Decoding Process
29/07/2023 Dr. Sadiq 30
00
01
10
11

31. VITERBI Decoding Process
29/07/2023 Dr. Sadiq 31
00
01
10
11

32. VITERBI Decoding Process
29/07/2023 Dr. Sadiq 32
00
01
10
11

33. VITERBI Decoding Process
29/07/2023 Dr. Sadiq 33
00
01
10
11

34. VITERBI Decoding Process
29/07/2023 Dr. Sadiq 34
00
01
10
11

35. VITERBI Decoding Process
29/07/2023 Dr. Sadiq 35
00
01
10
11

36. VITERBI Decoding Process
29/07/2023 Dr. Sadiq 36
00
01
10
11

37. 29/07/2023 Dr. Sadiq 37
Quiz
• Draw Trellis Diagram for the following Convolution
Diagram.
Input data bits Output coded bits
m
1
u
2
u
First coded bit
Second coded bit
2
1,u
u
(Branch word)
1
g
2
g

38. 29/07/2023 Dr. Sadiq 38
Free distance of Convolutional codes
• Since a Convolutional encoder generates
codewords with various sizes (as opposite to the
block codes), the following approach is used to
find the minimum distance between all pairs of
codewords:
– Since the code is linear, the minimum distance of the
code is the minimum distance between each of the
codewords and the all-zero codeword.
– This is the minimum distance in the set of all arbitrary
long paths along the trellis that diverge and remerge
to the all-zero path.
– It is called the minimum free distance or the free
distance of the code, denoted by
f
free d
d or

39. 29/07/2023 Dr. Sadiq 39
Free distance …
2
0
1
2
1
0
2
1
1
2
1
0
0
2
1
1
0
2
0
6
t
1
t 2
t 3
t 4
t 5
t
Hamming weight
of the branch
All-zero path
The path diverging and remerging to
all-zero path with minimum weight
5

f
d

40. 29/07/2023 Dr. Sadiq 40
Interleaving
• Convolutional codes are suitable for memoryless
channels with random error events.
• Some errors have bursty nature:
– Statistical dependence among successive error
events (time-correlation) due to the channel
memory.
– Like errors in multipath fading channels in wireless
communications, errors due to the switching
noise,
• “Interleaving” makes the channel looks like as a
memoryless channel at the decoder.

41. 29/07/2023 Dr. Sadiq 41
Interleaving
• Interleaving is done by spreading the coded symbols
in time (interleaving) before transmission.
• The reverse in done at the receiver by de-interleaving
the received sequence.
• “Interleaving” makes bursty errors look like random.
Hence, Conv. codes can be used.

42. Interleaving and De-Interleaving
29/07/2023 Dr. Sadiq 42
Interleaving is heavily used in wireless communication for protection against burst
errors

43. 29/07/2023 Dr. Sadiq 43
Interleaving …
– Consider a code with t=1 and 3 coded bits.
– A burst error of length 3 can not be corrected.
– Let us use a block Interleaver 3X3
A1 A2 A3 B1 B2 B3 C1 C2 C3
2 errors
A1 A2 A3 B1 B2 B3 C1 C2 C3
Interleaver
A1 B1 C1 A2 B2 C2 A3 B3 C3
A1 B1 C1 A2 B2 C2 A3 B3 C3
Deinterleaver
A1 A2 A3 B1 B2 B3 C1 C2 C3
1 errors 1 errors 1 errors

44. Interleaving/De-Interleaving
29/07/2023 Dr. Sadiq 44

45. Interleaving De-interleaving
29/07/2023
1) Sender writes row-by-
row into buffer
2) Read col-by-col from
buffer onto link
1) Write col-by-col from
link into buffer
2) Receiver reads row-by-
row from buffer
45
Dr. Sadiq

46. Interleaving Example
29/07/2023 Dr. Sadiq 46

47. 29/07/2023 Dr. Sadiq 47
Concatenated codes
• A concatenated code uses two levels on coding, an inner code
and an outer code (higher rate).
• The purpose of concatenated codes is to reduce the overall
complexity, yet achieving the required error performance.
• Solution: Concatenate two (or more) codes
– This creates a much more powerful code.
• Serial Concatenation (Forney, 1966)
Interleaver Modulate
Deinterleaver
Inner
encoder
Inner
decoder
Demodulate
Channel
Outer
encoder
Outer
decoder
Input
data
Output
data

48. Parallel Concatenated Codes
• Instead of concatenating in serial, codes can also be concatenated
in parallel.
• Example: Turbo code is a parallel concatenation of two systematic
Convolutional codes
• An systematic Convolutional encoder can be constructed from a
standard Convolutional encoder by feeding back one of the
outputs.
– systematic: one of the outputs is the input.
D D
i
m )
0
(
i
x
)
1
(
i
x
i
x
i
r
)
0
(
i
x
D D
i
m
)
1
(
i
x
i
x
29/07/2023 Dr. Sadiq 48

49. Convolutional Code Used in WIMAX
29/07/2023 Dr. Sadiq 49

50. Convolutional Code Used in CDMA2000
29/07/2023 Dr. Sadiq 50

51. Convolutional Code Used in WCDMA
29/07/2023 Dr. Sadiq 51