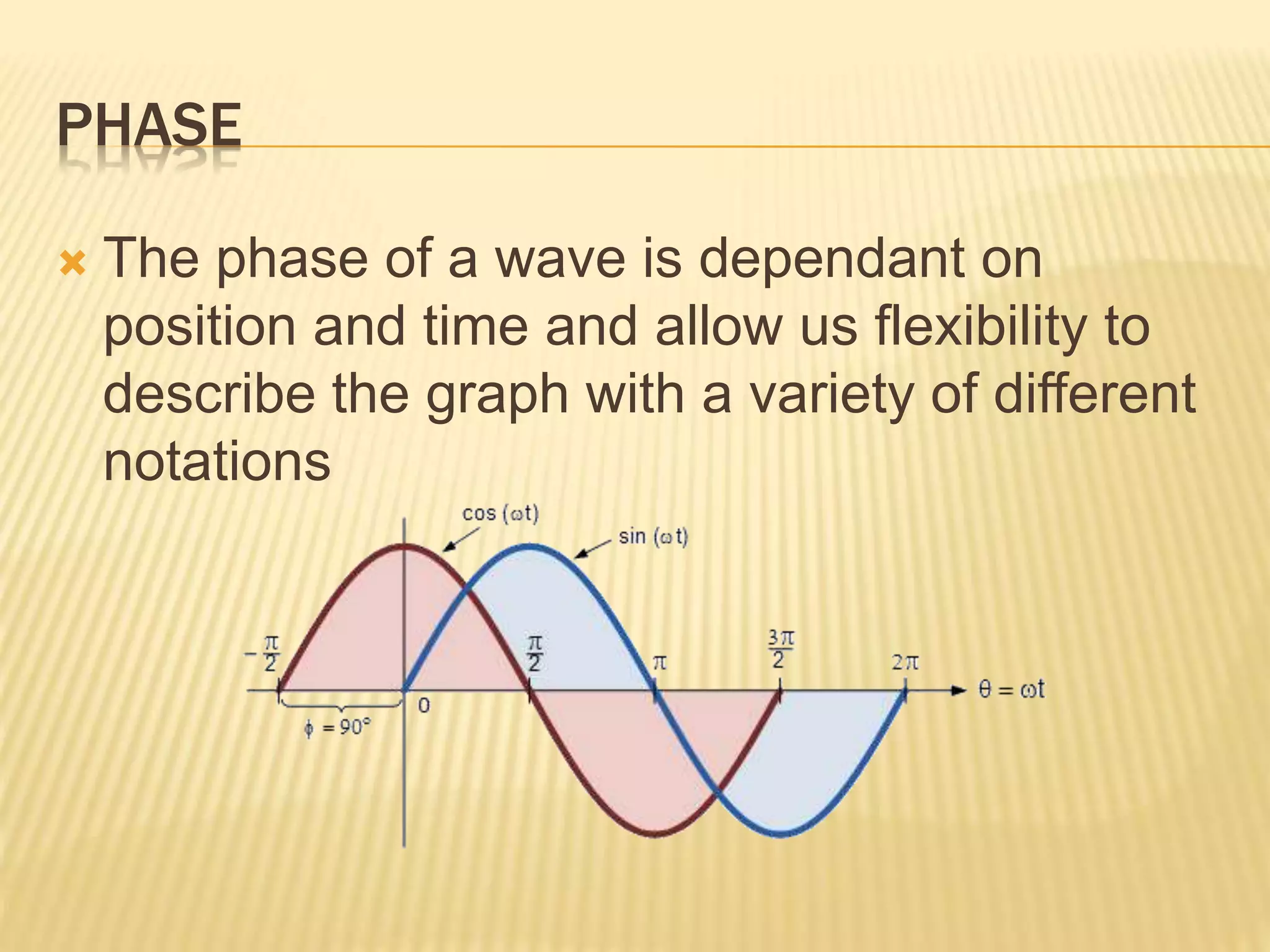
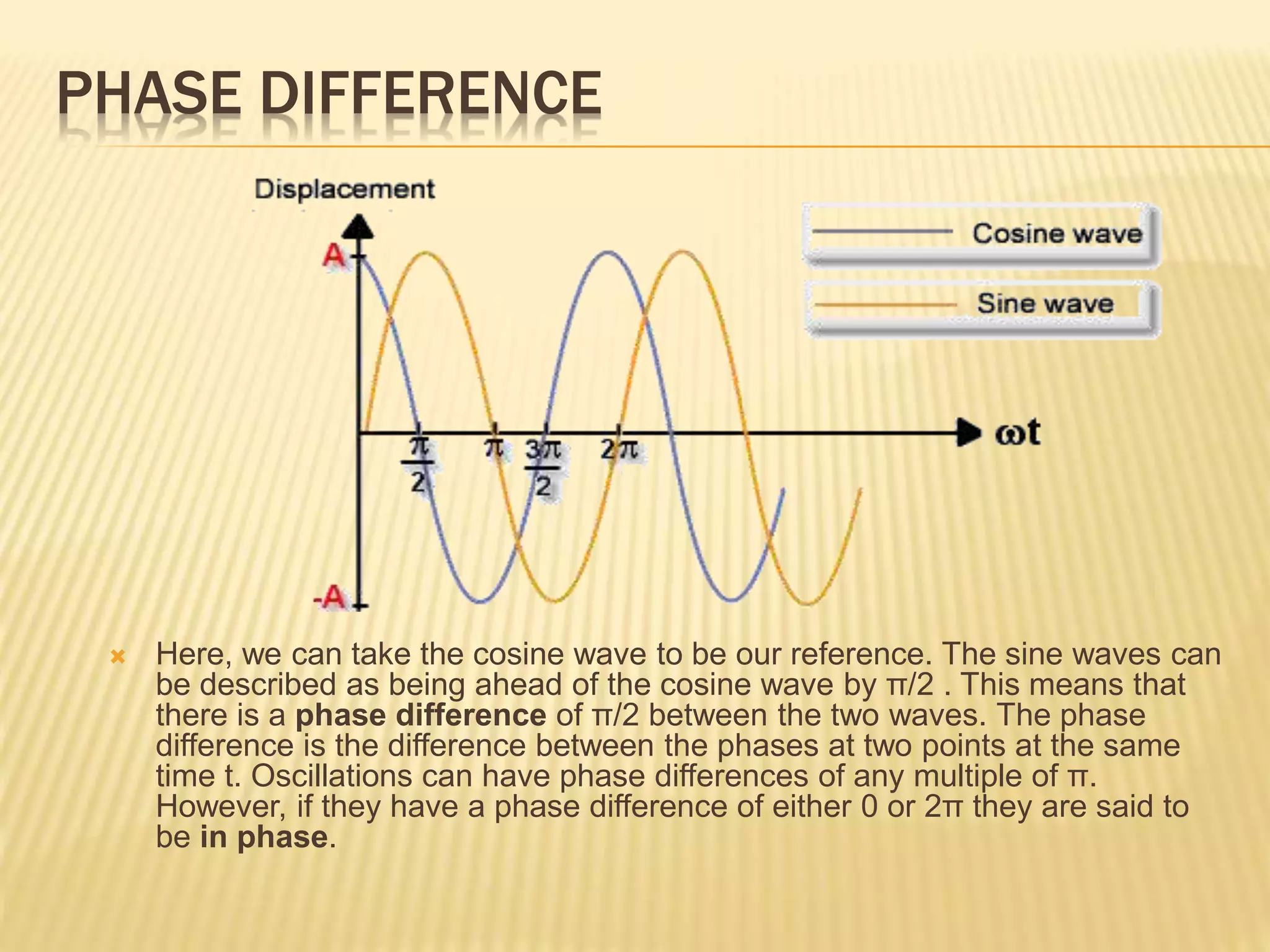
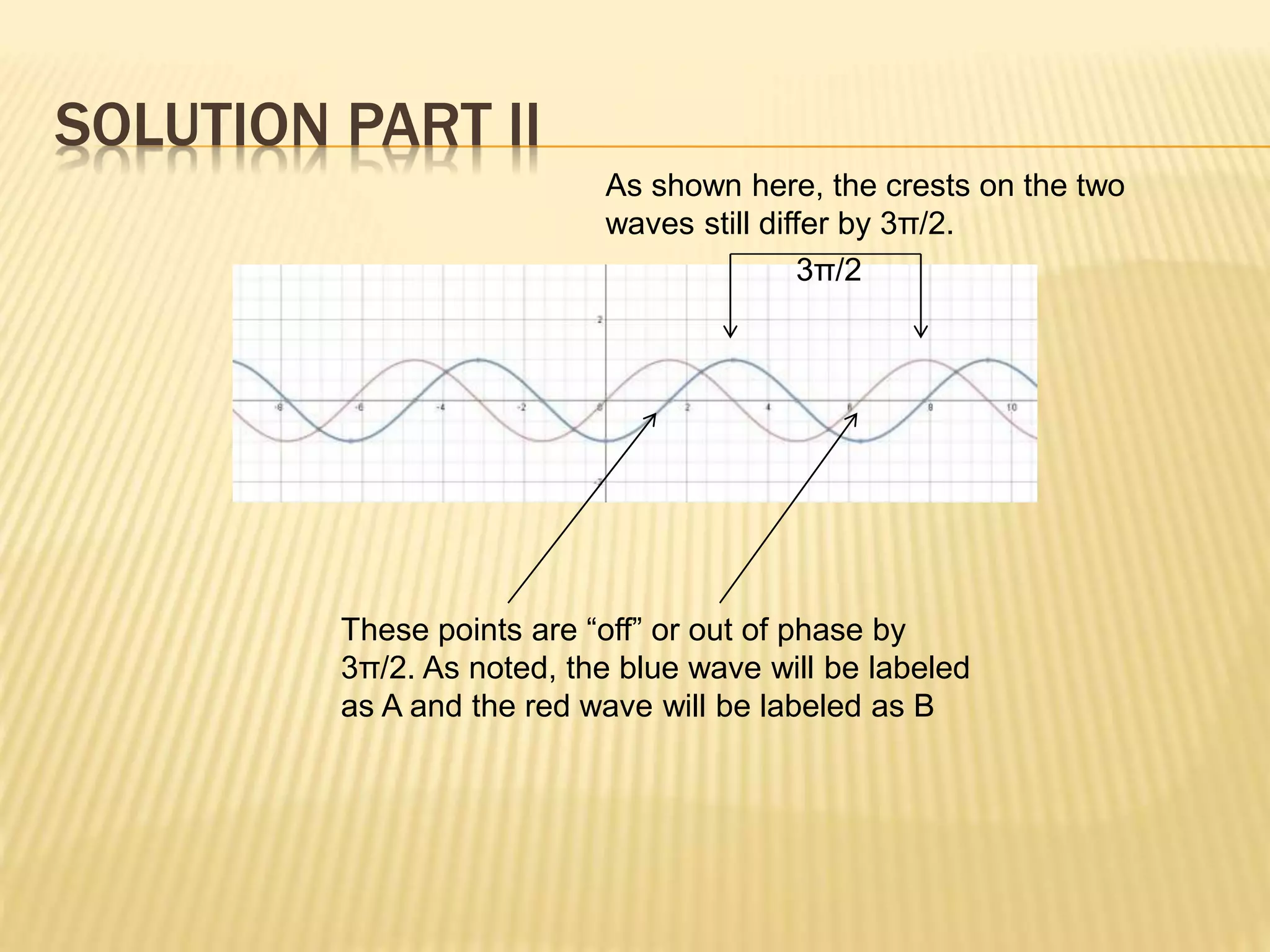
This document discusses phase and phase difference in waves. It provides definitions of standing waves, which have nodes where the wave disturbance is minimal, and traveling waves, which do not have nodes. The displacement equation for traveling waves includes a term for velocity (v) to account for waves moving in the positive or negative x direction. Phase describes the wave's position and time, while phase difference is the difference in phases between two waves at the same time. A worked example shows waves A and B with a phase difference of 3π/2, and calculates their distance apart as 3λ/4, where λ is the wavelength.

1. PHASE AND PHASE DIFFERENCE
Learning Objects 3 Physics 101

2. A BIT OF REVIEW:
 You may remember learning
about standing waves in the
past. These waves oscillate
and create regions where
the disturbance of the wave
is almost zero. These
‘nodes’ create the illusion
that the wave is standing
still.

3. A BIT OF REVIEW
 In comparison, travelling
waves do not have nodes
and hence the wave is
seen to ‘travel’ and alter its
displacement from its
equilibrium position as
time progresses

4. EQUATIONS
 The (x) in the usual displacement equation:
 D(x) = Asin(kx)
 Is now replaced with:
 (x-vt) for waves traveling in the positive x direction
 (x+vt) for waves traveling in the negative x direction
 Compared to the previous equation, the new variables allow
room for us to shift the graph by shifting it by a phase
difference

5. PHASE
 The phase of a wave is dependant on
position and time and allow us flexibility to
describe the graph with a variety of different
notations

6. PHASE DIFFERENCE
 Here, we can take the cosine wave to be our reference. The sine waves can
be described as being ahead of the cosine wave by π/2 . This means that
there is a phase difference of π/2 between the two waves. The phase
difference is the difference between the phases at two points at the same
time t. Oscillations can have phase differences of any multiple of π.
However, if they have a phase difference of either 0 or 2π they are said to
be in phase.

7. QUESTION
 A harmonic wave A has a phase difference of
3π/2 ahead of harmonic wave B.
 Part I: Sketch and label the two waves.
 Part II: Show the relationship between the phase
difference in the question above and the distance
between points (x) in multitudes of wavelength
(λ)

8. SOLUTION PART II
These points are “off” or out of phase by
3π/2. As noted, the blue wave will be labeled
as A and the red wave will be labeled as B
As shown here, the crests on the two
waves still differ by 3π/2.
3π/2

9. SOLUTION PART II
 = 2π (∆ x/λ)
 We know that the phase difference ∆Φ is
given to us in the equation as 3π/2
 Plugging this number into the equation and
solving for ∆x yields:
 ∆x =3π/2 = 2π (∆ x/λ)
 Giving us the answer: ∆x=3 λ /4