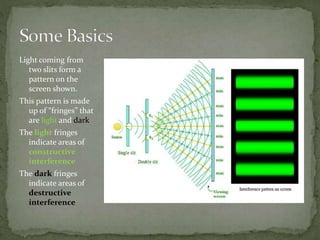
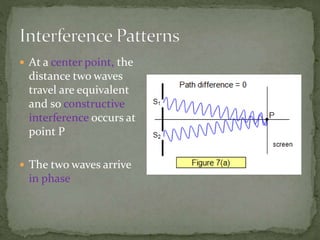
The document describes the principles of interference patterns produced in a double-slit experiment. Light passing through two slits forms a pattern of bright and dark fringes on a screen due to constructive and destructive interference. The spacing between fringes can be calculated based on the wavelength of light, distance between the slits, and distance from the slits to the screen. If the distance between the slits increases, the spacing between adjacent bright fringes will decrease. When two light sources with different wavelengths are used, the order of fringes can be determined such that a bright fringe of one wavelength aligns with a dark fringe of the other.

1. Vivian Tsang LO9 14153143

2. Light coming from
two slits form a
pattern on the
screen shown.
This pattern is made
up of “fringes” that
are light and dark
The light fringes
indicate areas of
constructive
interference
The dark fringes
indicate areas of
destructive
interference

3.  At a center point, the
distance two waves
travel are equivalent
and so constructive
interference occurs at
point P
 The two waves arrive
in phase

4.  The lower wave travels one
wavelength farther than the
upper wave.
 The waves arrive in phase at
the point indicated
 This results in a bright fringe
 Constructive interference
occurs
d

5.  Constructive interference
 Path difference must be zero or an integral multiple of the
wavelength
 Variables
 θm= =the angle shown in the previous slide
 λ=wavelength
 d= distance between the two slits
 dsin(θm)=mλ
 m=….-3, -2, -1, 0, 1, 2, 3……etc
 m=order number of the fringes
 (ie: m= -/+2 is the second order bright fringe

6.  Assuming paths of
travelling light are
parallel because
the distance
between the
screens is large
L>>d
ymbright
L

7.  If we approximate tan(x)~sin(x)
 y~Lsin(θ) for small angles
 Therefore…
 sin(θ)=y/L
 Spacing between two bright fringes can be calculated by:
 ymbright=m λL/d
 As indicated on the previous slide:
 ymbright=the vertical distance between center of screen to the
bright fringe
 L= the horizontal distance between the slits and the screen

8.  The lower wave travels half a
wavelength farther than the
upper wave.
 The waves arrive out of
phase at the point indicated
 This results in a dark fringe
 Destructive interference
occurs

9.  Therefore…
 sin(θ)=y/L
 Spacing between two dark fringes can be calculated
by:
 ymdark=((m+0.5)λL)/d m=….-3, -2, -1, 0, 1, 2, 3……etc

10.  If the distance between two sources are increased, the
spacing between adjacent bright fringes will…
 Increase
 Decrease
 Stay the same

11.  Decrease
 Reason:
 ymbright=m λL/d
 If d increases that will increase the denominator of the
equation. This in turn will decrease the value of y
 Therefore, the spacing between adjacent bright fringes
decreases

12.  A light source consists of two types of gasses that emit
light at 550nm and 400nm. The source is used in a
double slit experiment.
 Note: assume that these sources do not interfere with
each other
 What is the lowest order 550nm bright fringe that will
fall on a 400nm dark fringe?
 What are their corresponding orders?

13.  λ1=a= 550nm (bright)
 y1= (m1aL)/d)
 λ2=b=400nm (dark)
 y2= ((m2+0.5)bL)/d

14.  y1=y2
 (m1aL)/d) = ((m2+0.5)bL)/d
 (m1a) = ((m2+0.5)b)
 (m1550) = ((m2+0.5)400)
 550m1=400m2+200
 400(m2-m1)=150m1-200
 Therefore, 150m1-200 must be a multiple of 400

15.  Thus this will generate two answers:
 400(m2-m1)=150m1-200
 The lowest m1 where the RHS can be a multiple of 400
requires m1 to be =4
 150(4)-200=400
 Plugging m1=4 into the equation above gives us m2=5
 Another interpretation leads us to conclude that m1 is =-4
 150(-4)-200=-800
 Plugging m1=-4 into the equation above gives us m2=6
 Therefore:
 m1=4, m2=5
 m1=-4, m2=6