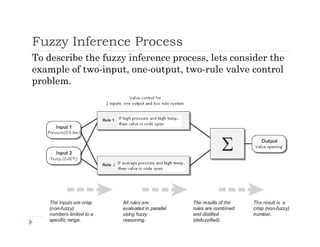
This document provides an overview of fuzzy logic. It begins by defining fuzzy as not being clear or precise, unlike classical sets which have clear boundaries. It then explains fuzzy logic allows for partial set membership rather than binary membership. The document outlines fuzzy logic's ability to model imprecise or nonlinear systems using natural language-based rules. It details the key concepts of fuzzy logic including linguistic variables, membership functions, fuzzy set operations, fuzzy inference systems and the 5-step fuzzy inference process of fuzzifying inputs, applying fuzzy operations and implications, aggregating outputs and defuzzifying results.

1. Fuzzy Logic
Presented by: Mahesh Todkar

2. Content
What is Fuzzy?
Sets Theory
What is Fuzzy Logic?
Why use Fuzzy Logic?
Theory of Fuzzy Sets
Vocabulary
Fuzzy if-then Rules
Fuzzy Logic Operations
Fuzzy Inference Systems (FIS)
Fuzzy Inference Process
References

3. What is Fuzzy?
Fuzzy means
not clear, distinct or precise;
not crisp (well defined);
blurred (with unclear outline).

4. Sets Theory
Classical Set: An element either belongs or does not
belong to a sets that have been defined.
Fuzzy Set: An element belongs partially or gradually to
the sets that have been defined.

5. What is Fuzzy Logic?
It has two different meanings as,
In narrow sense: Fuzzy logic is a logical system,
which is an extension of multi-valued logic.
In a wider sense: Fuzzy logic (FL) is almost
synonymous with the theory of fuzzy sets, a theory
which relates to classes of objects with unsharp
boundaries in which membership is a matter of
degree.
Fuzzy logic (FL) should be interpreted in its wider
sense

6. What is Fuzzy Logic?
A way to represent variation or imprecision in logic
A way to make use of natural language in logic
Approximate reasoning
Definition of Fuzzy Logic:
A form of knowledge representation suitable for
notions that cannot be defined precisely, but which
depend upon their contexts.
Superset of conventional (Boolean) logic that has been
extended to handle the concept of partial truth - the truth
values between "completely true & completely false".

7. Why use Fuzzy Logic?
Conceptually easy to understand
Flexible
Tolerant of imprecise data
FL can model nonlinear functions of arbitrary complexity
FL can be built on top of the experience of experts
FL can be blended with conventional control techniques
FL is based on natural language

8. Theory of Fuzzy Sets
Classical Set Fuzzy Set

9. Theory of Fuzzy Sets
Theory which relates to classes of objects with unsharp
boundaries in which membership is matter of degree
Thus every problem can be presented in terms of
Fuzzy Sets
A set without crisp
Fuzzy set describes vague concepts
Fuzzy set admits the possibility of partial membership
in it
Degree of an object belongs to Fuzzy Set is denoted by
membership value between 0 to 1
Membership Function (MF) associated with a given
Fuzzy Set maps an input value to its appropriate
membership value

10. Vocabulary
Linguistic Variable: Variable whose values are words
or sentences rather than numbers
It represent qualities spanning a particular spectrum
Example: Speed, Service, Tip, Temperature, etc.
Linguistic Value or Term: Values or Terms used to
describe Linguistic Variable
Example: For Speed (Slowest, Slow, Fast, Fastest), For
Service (Poor, Good, Excellent), For Temperature
(Freezing, Cool, Warm, Hot), etc.

11. Vocabulary
Universe of Discourse or Universe or Input Space (U):
Set of all possible elements that can come into
consideration, confer the set U in (1).
It depends on context.
Elements of a fuzzy set are taken from a Universe of
Discourse.
An application of the universe is to suppress faulty
measurement data.
Example:
Set of x >> 1 could have as a universe of all real numbers,
alternatively all positive integer.

12. Vocabulary
Membership Function (MF) is a curve that defines how
each point in the input space is mapped to a membership
value between 0 and 1.
It is denoted by µ.
Membership value is also called as degree of membership
or membership grade or degree of truth of proposal.
Types of Membership Functions:
Piece-wise linear functions
Gaussian distribution function
Sigmoid curve
Quadratic and cubic polynomial curves
Singleton Membership Function

13. Membership Functions

14. Syntax of Fuzzy Set
A = {x, µA(x) | x X}
Where,
A – Fuzzy Set
x – Elements of X
X – Universe of Discourse
µA(x) – Membership Function of x in A

15. Fuzzy if-then Rules
Statements used to formulate the conditional statements
that comprise fuzzy logic
Example:
if x is A then y is B
where,
A & B – Linguistic values
x – Element of Fuzzy set X
y – Element of Fuzzy set Y
In above example,
Antecedent (or Premise)– if part of rule (i.e. x is A)
Consequent (or Conclusion) – then part of rule (i.e. y is B)
Antecedent is interpretation & Consequent is assignment

16. Fuzzy if-then Rules
Antecedent is combination of proposals by AND, OR, NOT
operators
Consequent is combination of proposals linked by AND
operators. OR and NOT operators are not used in
consequents as these are cases of uncertainty.
Example:
If it is early, then John can study.
Universe: U = {4,8,12,16,20,24}; time of day
Input Fuzzy set: early = {(4,0),(8,1),(12,0.9),(16,0.7),(20,0.5),(24,0.2)}
Output Fuzzy set: can study=singleton Fuzzy set (assume) so study =1
i.e. at 20 (8 pm), early (20) = 0.5

17. Fuzzy if-then Rules
Interpreting if-then rule is a three–part process
1) Fuzzify Input: Resolve all fuzzy statements in the
antecedent to a degree of membership between 0 and 1.
2) Apply fuzzy operator to multiple part antecedents:
If there are multiple parts to the antecedent, apply fuzzy
logic operators and resolve the antecedent to a single
number between 0 and 1.
3) Apply implication method: The output fuzzy sets
for each rule are aggregated into a single output fuzzy
set. Then the resulting output fuzzy set is defuzzified, or
resolved to a single number.

18. Fuzzy if-then Rules
Interpreting if-then rule is a three–part process:

19. Fuzzy Logic Operations
Fuzzy Logic Operators are used to write logic
combinations between fuzzy notions (i.e. to perform
computations on degree of membership)
Zadeh operators
1) Intersection: The logic operator corresponding to
the intersection of sets is AND.
(A AND B) = MIN( (A), (B))
2) Union: The logic operator corresponding to the
union of sets is OR.
(A OR B) = MAX( (A), (B))
3) Negation: The logic operator corresponding to the
complement of a set is the negation.
(NOT A) =1- (A)

20. Fuzzy Logic Operations

21. Fuzzy Inference Systems (FIS)
Fuzzy Inference is the process of formulating the mapping
from a given input to an output using fuzzy logic.
Process of fuzzy inference involves Membership Functions
(MF), Logical Operations and If-Then Rules.
FIS having multidisciplinary nature, so cab called as
fuzzy-rule-based systems, fuzzy expert systems, fuzzy
modeling, fuzzy associative memory, fuzzy logic
controllers, and simply (and ambiguously) fuzzy systems.
Types of FIS:
1) Mamdani-type: Most commonly used. Expects the output MF’s to
be fuzzy sets.
2) Sugeno-type: Output MF’s are either linear or constant.

22. Fuzzy Inference Process
To describe the fuzzy inference process, lets consider the
example of two-input, one-output, two-rule valve control
problem.

23. Fuzzy Inference Process
Step 1: Fuzzify Input (Fuzzification)
Take the inputs and determine the degree to which they
belong to each of the appropriate fuzzy sets via
membership functions.
Input is always a crisp numerical value limited to the
universe of discourse of the input variable.
Output is a fuzzy degree of membership in the
qualifying linguistic set.
Each input is fuzzified over all the qualifying
membership functions required by the rules.

24. Fuzzy Inference Process
Step 1: Fuzzify Input (Fuzzification)

25. Fuzzy Inference Process
Step 2 : Apply Fuzzy Operator
If the antecedent of a given rule has more than one
part, the fuzzy operator is applied to obtain one
number that represents the result of the antecedent
for that rule.
The input to the fuzzy operator is two or more
membership values from fuzzified input variables.
The output is a single truth value.

26. Fuzzy Inference Process
Step 2 : Apply Fuzzy Operator

27. Fuzzy Inference Process
Step 3: Apply Implication Method
First must determine the rule’s weight.
Operation in which the result of fuzzy operator is used to
determine the conclusion of the rule is called as
implication.
The input for the implication process is a single number
given by the antecedent.
The output of the implication process is a fuzzy set.
Implication is implemented for each rule.

28. Fuzzy Inference Process
Step 3: Apply Implication Method
Antecedent Consequent

29. Fuzzy Inference Process
Step 4 : Aggregate All Outputs
Aggregation is the process by which the fuzzy sets that
represent the outputs of each rule are combined into a
single fuzzy set.
Aggregation only occurs once for each output variable.
The input of the aggregation process is the list of
truncated output functions returned by the implication
process for each rule.
The output of the aggregation process is one fuzzy set
for each output variable.

30. Fuzzy Inference Process
Step 4 : Aggregate All Outputs

31. Fuzzy Inference Process
Step 5: Defuzzify
Move from the “fuzzy world” to the “real world” is
known as defuzzification.
The input for the defuzzification process is a fuzzy set.
The output is a single number.
The most popular defuzzification method is the
centroid calculation, which returns the center of area
under the curve
Other methods are bisector, middle of maximum (the
average of the maximum value of the output set),
largest of maximum, and smallest of maximum.

32. Fuzzy Inference Process
Step 5: Defuzzify

33. References
Fuzzy Logic Toolbox™ 2 User’s Guide
Tutorial On Fuzzy Logic by Jan Jantzen
Fuzzy Logic by Cahier Technique Schneider

34. Thank You…

35. Any Questions?