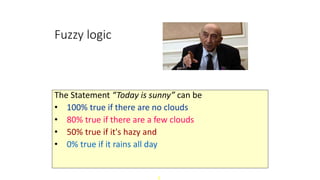
Fuzzy logic is a form of logic that accounts for partial truth and degrees of truth. It is based on the concept that the transition between two states is gradual rather than abrupt. Fuzzy logic allows intermediate values between conventional evaluations like true/false, yes/no, high/low. This document discusses classical logic, Boolean logic, fuzzy sets, fuzzy membership functions, fuzzy rules, and fuzzy inference systems. It provides examples of how fuzzy logic can be used to represent imprecise concepts like "around 220V" or "fairly high temperature" through assigning membership values between 0 and 1.

1. Fuzzy Logic
Dr. Umang Soni

2. Classical Logic
2
 Invented by ancient Greeks,
 used by mathematicians
In this logic
 Every statement is either TRUE or FALSE
 Statements can be combined with the logical connections:
AND and OR
 A statement can be modified with NOT
 Truth tables are used to evaluate the truth value of a complicated
statement (i.e., TRUEness or FALSEness)
 Logical IF–THEN statements are used to express “THEOREMS”
BRIEF HISTORY
Aristotle
Socrates

3. INTRODUCTION
• It is the mark of an instructed mind to rest satisfied with that degree of
precision which the nature of the subject admits, and not to seek exactness
where only an approximation of the truth is possible.
Aristotle, 384–322 BC (Ancient Greek philosopher)
• Precision is not truth , Henri E. B. Matisse, 1869–1954
• All traditional logic habitually assumes that precise symbols are being
employed. It is therefore not applicable to this terrestrial life but only to an
imagined celestial existence.
Bertrand Russell, 1923

4. • Most engineering texts do not address the uncertainty in the information, models,
and solutions that are conveyed within the problems addressed therein.
• The more complex a system is, the more imprecise or inexact is the information that
we have to characterize that system. It seems, then, that precision, information and
complexity are inextricably related in the problems we pose for eventual solution.
• However, for most of the problems that we face, we can do a better job in accepting
some level of imprecision.
• It seems intuitive that we should balance the degree of precision in a problem with
the associated uncertainty in that problem

5. Boolean Logic
5
• Based on Classical Logic
• In Boolean logic, we use only two possible values, called by various names,
such as
"true" and "false",
"yes" and "no",
"on" and "off“,
"1" and "0".
 Formulas evaluate truth values
• 1854: Logical algebra was published by George Boole
 known today as “Boolean Algebra”
 It’s a convenient and systematic way of expressing and analyzing the
operation of “logic circuits”.
• 1938: Boole’s work was applied to the analysis and design of logic circuits by
Claude Shannon.
BRIEF HISTORY
George Boole

6. 6
Boolean Logic
In Boolean logic, each element either belongs to or
does not belong to a set.
If an element is a member of a given set, the Boolean
logic will return :
1 (representing complete membership)
0 (representing non-membership)

7. 1
Boolean Logic
If A represents an ordinary crisp set/ Boolean set
Then A ={x | P(x)} indicates that the set A consists of those items
x for which the property P is true.
For example:
“THE BULB GLOWS AT A SUPPLY VOLTAGE OF 220V”
According to this statement the bulb will glow at 220V and not otherwise.
216 218 220 222 224 226
GLOW, 1
NOT GLOW, 0
BOOLEAN REPRESENTATION

8. 8
1
Fuzzy logic
The Statement “Today is sunny” can be
• 100% true if there are no clouds
• 80% true if there are a few clouds
• 50% true if it's hazy and
• 0% true if it rains all day

9. 9
1
Basics of Fuzzy Logic…
The condition “around 220V” cannot be represented by either 1 or 0, although the
human mind can very well comprehend that it refers to voltages little below or
higher than 220V. Thus “ around 220V” is not a binary /crisp condition. i.e. two
distinct states 1 and 0 are not enough to characterize it. So one might be inclined to
say that we require more states or multiple states. But how many states?
214 216 218 220 222 224 226
FUZZY REPRESENTATION
1
0
Now consider the statement “The bulb glows when supply voltage is "around
220V”
According to this statement , the bulb will glow even for voltages lower as well as
higher than 220V.
THE ANSWER LIES WITH FUZZY LOGIC

10. 10
Basics of Fuzzy Logic…
The terms like AROUND, APPROXIMATELY, MORE-OR-LESS,
SLIGHTLY, VERY represent an intuitive feel of expert human and
can be expressed as FUZZY SETS.
FUZZY SET
Fuzzy set is a mathematical measure of ambiguous phenomenon
and a technique for mathematically expressing linguistics
ambiguity.
The phrase” around 220V” can be represented by a set of points.
Each point is a measure of the degree to which the phrase”
around 220V” is true.

11. 11
Basics of Fuzzy Logic…
• The collection of points which determine the curve “AROUND
220V” can be written in the form
• The ∫ and  do not represent the conventional integration or
differentiation signs, but they only denote the collection of
points which form the set F. F is called a fuzzy Set.
• F= AROUND 220V = [0/208, 0.1/210, 0.2/212, 0.4/214,
0.6/216, 0.8/217, 1/220, 0.8/224, 0.6/226, 0.2/230, 0/234]
(x)/x
μ
OR F
(x)/x
μ
F
u
F
u
F 
 


12. • Suppose set A is the crisp set of all people with 5.0 ≤ x ≤ 7.0 feet.
• A particular individual, x1, has a height of 6.0 feet. The membership of this
individual in crisp set A is equal to 1, or full membership, given symbolically as
χA(x1) = 1.
• Another individual, say x2, has a height of 4.99 feet. The membership of this
individual in set A is equal to 0, or no membership, hence χA(x2) = 0.
• In these cases the membership in a set is binary, either an element is a member of
a set or it is not.
Membership functions for a crisp set A

13. • The sets on the universe X that can accommodate “degrees of membership”
were termed by Zadeh as fuzzy sets.
• Continuing further on the example on heights, consider a set H, consisting of
heights near 6 feet .
• Since the property near 6 feet is fuzzy, there is no unique membership function
for H.
• Rather, the analyst must decide what the membership function, denoted μH,
should look like.
Membership functions for a fuzzy set H.

14. • A key difference between crisp and fuzzy sets is their membership
function; a crisp set has a unique membership function, whereas a
fuzzy set can have an infinite number of membership functions to
represent it.
• For fuzzy sets, the uniqueness is sacrificed, but flexibility is gained
because the membership function can be adjusted to maximize the
utility for a particular application.

15. Fuzzy Set Operations
• Define three fuzzy sets A, B, and C on the universe X.
• For a given element x of the universe, the following function-theoretic
operations for the set-theoretic operations of union, intersection, and
complement are defined for A ,B, and C on X:
• Union μA∪B(x) = μA(x) ∨ μB(x) = max(A(x), B(x))
• Intersection μA∩B(x) = μA(x) ∧ μB(x) = min(A(x), B(x))
• Complement μ Ā(x) = 1 − μA(x)

16. Membership functions
• A triangular membership function is specified by three parameters {a,
b, c}:
• Triangle(x; a, b, c) = 0 if x  a;
• = (x-a)/(b-a) if a  x  b;
• = (c-b)/(c-b) if b  x  c;
• = 0 if c  x.

17. A trapezoidal membership function is specified by four
parameters {a, b, c, d} as follows:
Trapezoid(x; a, b, c, d) = 0 if x  a;
= (x-a)/(b-a) if a  x  b;
= 1 if b  x  c;
= (d-x)/(d-c) 0 if c  x  d;
= 0, if d  x.

18. A sigmoidal membership function is specified by two
parameters {a, c}:
• Sigmoid(x; a, c) = 1/(1 + exp[-a(x-c)]) where a controls slope at the
crossover point x = c.
• These membership functions are some of the commonly used
membership functions in the fuzzy inference systems.

19. Fuzzy Rules
• Fuzzy rules are useful for modeling human thinking, perception and
judgment.
• A fuzzy if-then rule is of the form “If x is A then y is B” where A and B
are linguistic values defined by fuzzy sets on universes of discourse X
and Y, respectively.
• “x is A” is called antecedent and “y is B” is called consequent.

20. Binary fuzzy relation
• A binary fuzzy relation is a fuzzy set in X × Y which maps each
element in X × Y to a membership value between 0 and 1. If X and Y
are two universes of discourse, then
• R = {((x,y), R(x, y)) | (x,y) Є X × Y } is a binary fuzzy relation in X × Y.
• X × Y indicates cartesian product of X and Y

21. Fuzzy rule as a relation
21
B
A
in
)
,
(
of
those
into
B
in
and
A
in
of
degrees
membership
the
ing
transform
of
task
the
performs
,
function"
n
implicatio
fuzzy
"
is
f
where
)
)
(
),
(
(
f
)
,
(
function
membership
dim
-
2
set with
fuzzy
a
considered
be
can
)
,
R(
)
B(
)
A(
:
)
,
R(
relation
by
d
represente
be
can
)
B(
then
),
A(
If
)
B(
),
A(
predicates
fuzzy
B
is
A,
is
B
is
then
A,
is
If
R



y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
B
A 



22. Fuzzy implications
22

23. Example of Fuzzy implications
23
 










)
,
/(
)
(
)
(
B
A
h)
R(t,
R(h)
R(t)
:
h)
R(t,
B
is
h
:
R(h)
A,
is
t
:
R(t)
B
is
h
then
A,
is
t
If
:
h)
R(t,
as
rewritten
be
can
rule
then the
H
B
,
high"
fairly
"
B
T
A
,
high"
"
A
H.
h
and
T
t
variables
define
and
humidity,
and
re
temperatu
of
universe
be
H
and
T
Let
h
t
h
t B
A 


24. Example of Fuzzy implications
24
 


 )
,
/(
)
(
)
(
B
A
h)
R(t, h
t
h
t B
A 

h
t
20 50 70 90
20 0.1 0.1 0.1 0.1
30 0.2 0.5 0.5 0.5
40 0.2 0.6 0.7 0.9

25. Example of Fuzzy implications
25
T
A
,
A
is
or t
high"
fairly
is
e
temperatur
"
When '
'

)
,
(
R
)
R(
)
R(
R(h)
find
to
relations
fuzzy
of
n
compositio
use
can
We
C
'
h
t
t
h 

h
t
20 50 70 90
20 0.1 0.1 0.1 0.1
30 0.2 0.5 0.5 0.5
40 0.2 0.6 0.7 0.9

26. Representation of Fuzzy Rule
26
Fact: is ' : ( )
Rule: If is then is : ( , )
Result: is ' : ( ) ( ) ( , )
u A R u
u A w C R u w
w C R w R u R u w

Single input and single output
' ' '
1 1 2 2
1 1 2 2
Fact: is ' and is ' and ... and is '
Rule: If is and is and ... and is then is
Result: is '
n n
n n
u A u A u A
u A u A u A w C
w C
Multiple inputs and single output
' ' '
1 1 2 2
1 1 2 2 1 1 2 2
Fact: is and is and ... and is
Rule: If is and is and ... and is then is , is ,..., is
Res
n n
n n m m
u A u A u A
u A u A u A w C w C w C
' ' '
1 1 2 2
ult: is , is ,..., is
m m
w C w C w C
Multiple inputs and Multiple outputs

27. Representation of Fuzzy Rule
27
Multiple rules
m
'
m
2
'
2
1
'
1
mj
'
mj
2j
'
2j
1j
'
1j
2
2
1
1
2
2
1
1
C
is
w
...,
,
C
is
w
,
C
is
w
:
Result
C
is
w
...,
,
C
is
w
,
C
is
then w
,
is
and
...
and
is
and
is
If
:
j
Rule
is
and
...
and
is
and
is
:
Fact
nj
'
n
j
j
'
n
'
n
'
A
u
A
u
A
u
A
u
A
u
A
u
'
'

28. Compositional rule of inference
28
The inference procedure is called as the “compositional rule of inference”. The
inference is determined by two factors : “implication operator” and
“composition operator”.
For the implication, the two operators are often used:
For the composition, the two operators are often used:

29. Representation of Fuzzy Rule
29
Max-min composition operator
Fact: is ' : ( )
Rule: If is then is : ( , )
Result: is ' : ( ) ( ) ( , )
u A R u
u A w C R u w
w C R w R u R u w

( , ):
R u w A C

Mamdani: min operator for the implication
Larsen: product operator for the implication