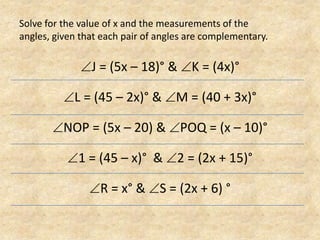The document defines and provides examples of complementary angles, supplementary angles, linear pairs, and vertical angles. It also states the Complement Theorem, Supplement Theorem, Linear Pair Postulate, and Vertical Angle Theorem. Several word problems are included where the value of x and angle measurements are solved for given complementary, supplementary, or congruent angle relationships.

1. Angle Pairs

2. Complementary AnglesComplementary angles are two angles whose measures have a sum of 90°.

3. Complementary AnglesThese two angles (40° and 50°) are complementary because they add up to 90°. But the angles don't have to be together.These two are complementary because27° + 63° = 90°.

4. Given that the two angles below are complementary, solve for the value of x and the angle measurements.mA 30mB  2x + 10 30° 60°mA + mB30 + 2x + 102x2xx909090 – 30 – 105025=====

5. Given that the two angles below are complementary, solve for the value of x and the angle measurements.mC 2x + 20mD  3x – 5 50° 40°mC + mD2x + 20 + 3x – 52x + 3x5xx909090 – 20 + 57515=====

6. Given that the two angles below are complementary, solve for the value of x and the angle measurements.mFEG 35 – xmGEH  45 + 2x 25° 65°mFEG + mGEH35 – x + 45 + 2x– x + 2xx909090 – 35 – 4510====

7. Solve for the value of x and the measurements of the angles, given that each pair of angles are complementary.J = (5x – 18)° & K = (4x)°L = (45 – 2x)° & M = (40 + 3x)°NOP = (5x – 20) & POQ = (x – 10)°1 = (45 – x)° & 2 = (2x + 15)°R = x° & S = (2x + 6) °

8. Solve for the value of x and the measurements of the angles, given that each pair of angles are complementary.J = (5x – 18)° & K = (4x)° 12 42 48L = (45 – 2x)° & M = (40 + 3x)° 5 35 55NOP = (5x – 20) & POQ = (x – 10)° 20 80 101 = (45 – x)° & 2 = (2x + 15)° 30 15 75R = x° & S = (2x + 6) ° 28 28 62

9. Supplementary AnglesSupplementary angles are two angles whose measures have a sum of 180°.

10. Supplementary AnglesThese two angles (140° and 40°) are supplementary because they add up to 180°. But the angles don't have to be together.These two are supplementary because27° + 63° = 180°.

11. Given that the two angles below are supplementary, solve for the value of x and the angle measurements.mT 50mV  3x + 40 50° 130°mT + mV50 + 3x + 403x3xX180180180 – 50 – 409030=====

12. Given that the two angles below are supplementary, solve for the value of x and the angle measurements.mW 3x – 55mX  155 – x 65° 115°mW + mX3x – 55 + 155 – x3x – x2xx180180180 + 55 – 1558040=====

13. Given that the two angles below are supplementary, solve for the value of x and the angle measurements.mBYA 3x + 5mAYZ  2x 110° 70°mBYA + mAYZ3x + 5 + 2x3x + 2x5xx180180180 – 517535=====

14. Solve for the value of x and the measurements of the angles, given that each pair of angles are supplementary.C = (2x – 2)° & D = (x – 34)°3 = (3x + 5)° & 4 = (5x + 5)°EFG = (x – 20)° & GFH = (x + 60)°J = (150 – x)° & K = (2x – 70)°LMN = (2x + 1)° & PQR = (3x – 1)°

15. Solve for the value of x and the measurements of the angles, given that each pair of angles are supplementary.C = (2x – 2)° & D = (x – 34)° 72 142 383 = (3x + 5)° & 4 = (5x + 5)° 15 100 80EFG = (x – 20)° & GFH = (x + 60)° 80 60 120J = (150 – x)° & K = (2x – 70)° 100 50 130LMN = (2x + 1)° & PQR = (3x – 1)° 36 73 107

16. The Complement Theorem: Complements of congruent angles are congruent. Given:C and O are complementary P and M are complementary O  M Prove: C  P

17. The Complement Theorem: Complements of congruent angles are congruent.STATEMENTC and O are complementaryP and M are complementaryO  MmC + mO = 90mP + mM = 90mC + mO = mP + mMmO = mMmC = mPC  PREASONGivenDefinition of complementary anglesTransitive Property of EqualityDefinition of congruent anglesSubtraction Property of EqualityDefinition of congruent angles

18. Theorem: If two angles are complementary and adjacent, then they form a right angle.

19. The Supplement Theorem: Supplements of congruent angles are congruent.

20. Linear PairA linear pair consists of two adjacent angles whose noncommon sides are opposite rays.Linear Pair Postulate: If two angles form a linear pair, then they are supplementary.

21. Vertical AnglesVertical angles are two nonadjacent angles formed by two intersecting lines.

22. Vertical Angle Theorem: Vertical angles are congruent.