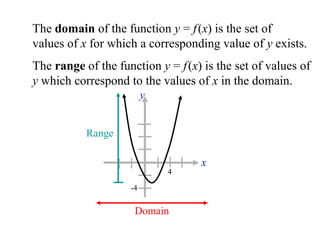
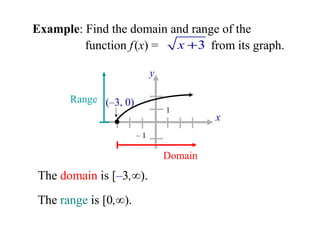
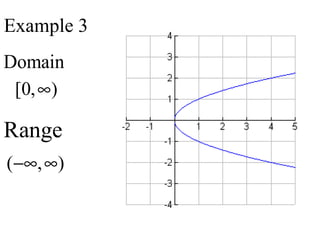
The document discusses domain and range for functions. It defines discrete and continuous functions. A discrete function has points that are not connected, while a continuous function forms a smooth, unbroken line or curve. Examples are given of determining the domain and range from graphs of continuous functions. The domain is the set of x-values for which there is a corresponding y-value. The range is the set of y-values. Homework problems on finding domain and range are assigned.

1. Warm-up
•
•
•
•
•
•
•
•
1. Given this relation:
{(2, -1), (4, -1), (3, 2), (5, 1), (4, 2), (5, 1)}
Domain?
Range?
Function or Not? Explain why?
2. Convert these to Interval Notation
x<6
2≤ x<5

2. Warm-up
•
•
•
•
•
1. Given this relation:
{(2, -1), (4, -1), (3, 2), (5, 1), (4, 2), (5, 2)}
Domain? {2,3,4,5}
Range? {-1,1,2}
Function or Not? NO, duplicated “x” values
• 2.
• x < 6 in interval notation (-∞, 6)
• 2 ≤ x < 5 in interval notation [2, 5)

3. Continuous Functions
vs
Discrete Functions
Domain and Range
Chapter 2
Section 2-1
Pages 72-81

4. Objectives
• I can determine Domain
and Range from a
Continuous Graph
• I can identify a discrete
and continuous function

5. Important Vocabulary
• Discrete Function
• Continuous Function

6. Discrete Function
• A function with ordered
pairs that are just points
and not connected.

7. Discrete Function

8. Continuous Functions??
• A function is continuous if it has an infinite
domain and forms a smooth line or curve
• Simply put: It has NO BREAKS!!!
• You should be able to trace it with your
pencil from left to right without picking up
your pencil
8

9. The domain of the function y = f (x) is the set of
values of x for which a corresponding value of y exists.
The range of the function y = f (x) is the set of values of
y which correspond to the values of x in the domain.
y
Range
4
-4
Domain
x

10. Example: Find the domain and range of the
x + 3 from its graph.
function f (x) =
y
Range (–3, 0)
1
–1
Domain
The domain is [–3,∞).
The range is [0,∞).
x

11. Example 1
Domain
(−∞, ∞)
Range
[−3, ∞)

12. Example 2
Domain
(−∞, ∞)
Range
(−∞, 4]

13. Example 3
Domain
[0, ∞)
Range
(−∞, ∞)

14. 8
Domain
(−∞, ∞)
6
4
Range
2
[2, ∞)
-5
5
-2

15. 6
Domain
(−∞,3]
4
Range
[1, ∞)
2
-5
5

16. Domain
(−∞, ∞)
Range
[0, ∞)

17. Domain
[0, ∞)
Range
[0, ∞)

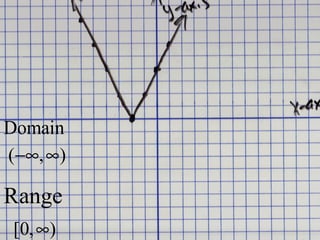
18. Domain
(−∞, −1) U [1, 6]
Range
(−∞, 6)

19. Homework
• WS 1-5: Domain and Range