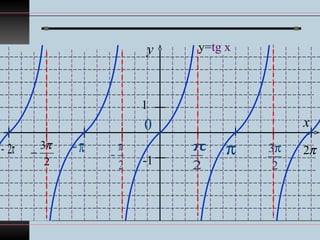
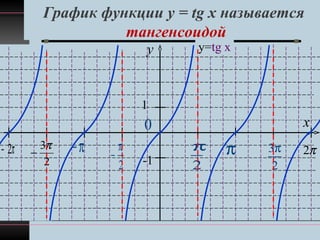
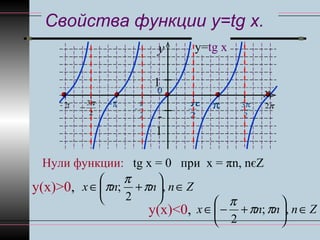
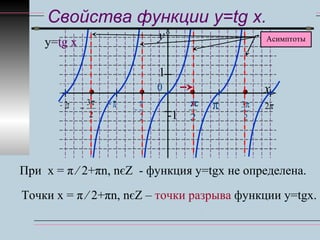
Документ описывает график функции y=tan x, называемой тангенсоидой, ее особенности и свойства, включая область определения, множество значений и периодичность. Он также рассматривает нули функции и точки разрыва, а также задачи по нахождению корней уравнения tan x = 2 и решения неравенства tan x ≤ 2 в заданном интервале. В работе представлены графики и разбивка на интервалы для нахождения решений.

1. Построение графика функции y=tg x.
х у=tg x
0 0
π ∕6 1 ∕ 3
π ∕4 1
π ∕3 3
π ∕2
Не
сущ.
y
x
1
-1
π
0
−π
2
π
2
π
−
у=tg x

2. y
x
1
-1
π
0
−π
2
π
2
π
−
у=tg x
3
2
π π2
2
3π
−π2−
График функции y = tg x называется
тангенсоидой

3. Функция y=tg x и её свойства.
1. Обл. определения:
2. Множество значений функции: уєR.
3. Периодическая, Т= π.
4. Нечётная функция.
5. Функция y=tg x возрастает на
промежутке
Znnх ∈+≠ ,
2
π
π
Znnn ∈





++− ,
2
;
2
π
π
π
π

4. Свойства функции y=tg x.
y
x
1
-
1
π
0
−π
2
π
2
π
−
у=tg x
3
2
π π2
2
3π
−π2−
Нули функции: tg х = 0 при х = πn, nєZ
у(х)>0,
у(х)<0,
Znnnх ∈





+∈ ,
2
; π
π
π
Znnnх ∈





+−∈ ,;
2
ππ
π

5. y
x
1
-1
π
0
−π
2
π
2
π
−
3
2
π π2
2
3π
−π2−
Свойства функции y=tg x.
у=tg x
При х = π ∕ 2+πn, nєZ - функция у=tgx не определена.
Точки х = π ∕ 2+πn, nєZ – точки разрыва функции у=tgx.
Асимптоты

6. Задача №1.
Отметьте на чертеже все корни уравнения
tgx=2 принадлежащих промежутку –π ≤ х ≤
3π ∕ 2.
y
x
1
-1
π
0
−π
2
π
2
π
−
3
2
π
2
3π
−
у=tg x
у=2
1. Построим графики
функций у=tgx и у=2
2. Отметим корни
х1х3 х2

7. Задача №2.
Найти все решения неравенства tgx ≤ 2
принадлежащих промежутку –π ≤ х ≤ 3π ∕ 2.
y
x
1
-1
π
0
−π
2
π
2
π
−
3
2
π
2
3π
−
у=tg x
у=2
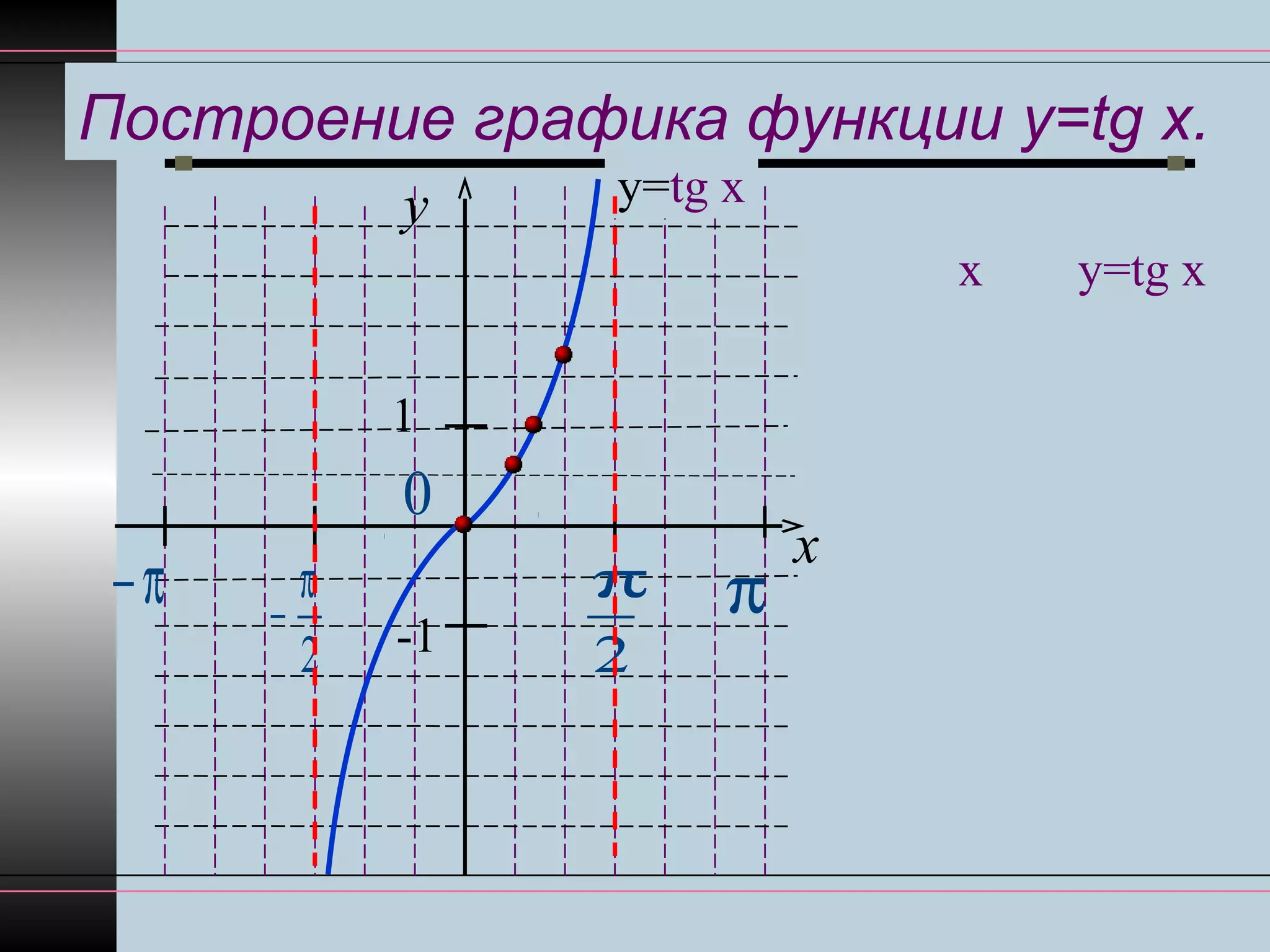
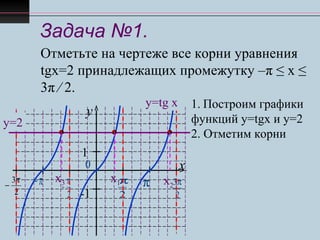
1. Построим графики
функций у=tgx и у=2
2. Отметим корни
уравнения tgx = 2
3. Ответ
х1х3 х2
3. хє[-π ; х3]U(-π ∕ 2; х1]U(π ∕ 2; х2]

8. y
x
1
-1
π
0
−π
2
π
2
π
−
у=tg x
3
2
π π2
2
3π
−π2−