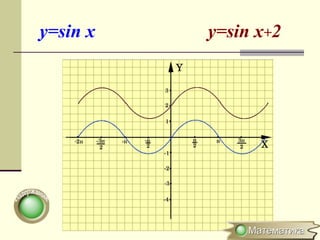
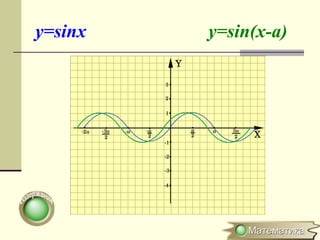
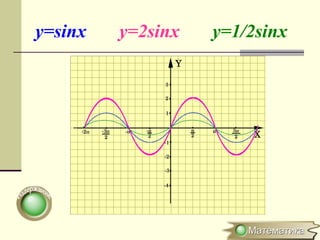
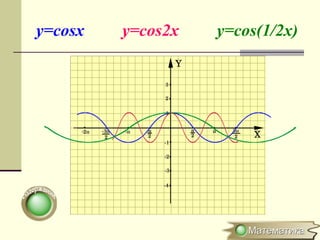
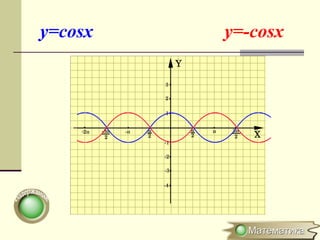
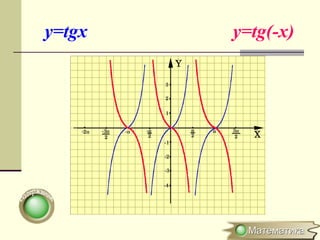
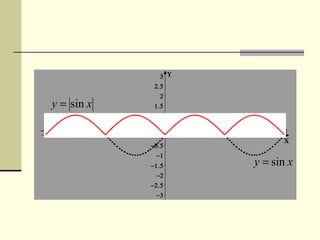
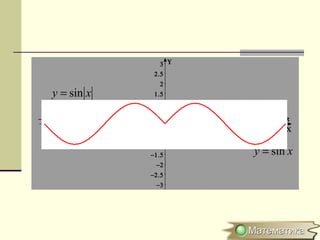
Документ описывает методы преобразования графиков функций, включая параллельные переносы, растяжения и симметричные отображения относительно осей координат. Рассматриваются конкретные примеры, такие как преобразования функций y=sin x и y=cos x. Кратко объясняется, как строить графики для модулей и абсолютных значений функций.

1. Преобразование графиков
функций

2. Содержание
 Параллельный перенос вдоль оси OY
 Параллельный перенос вдоль оси ОХ
 Растяжение (сжатие) в k раз вдоль оси OY
 Растяжение (сжатие) в k раз вдоль оси OХ
 Симметричное отображение относительно
оси OY
 Симметричное отображение относительно
оси OX
 Построение графика y=|f(x)|
 Построение графика y=f(|x|)

3. Параллельный перенос вдоль
оси OY
y=f(x) → y=f(x)+a
(x0;y0) → (x0;y0+a)
Для построения графика функции
y=f(x)+a необходимо график функции
y=f(x) перенести вдоль оси OY на
вектор (0;а)

4. y=sin x y=sin x+2

5. Параллельный перенос вдоль
оси ОХ
y=f(x) → y=f(x-a)
(x0;y0) → (x0+a;y0)
Для построения графика функции
y=f(x-a) необходимо график функции
y=f(x) перенести вдоль оси OX на
вектор (0;а)

6. y=sinx y=sin(x-a)

7. Растяжение (сжатие) в k раз вдоль
оси OY
y=f(x) → y=kf(x), где k>0
(x0;y0) → (x0;ky0)
Для построения графика функции y=kf(x)
необходимо график функции y=f(x)
растянуть в k раз вдоль оси ОY для k >1
или сжать в 1/k развдоль оси OY для k<1

8. y=sinx y=2sinx y=1/2sinx

9. Растяжение (сжатие) в k раз вдоль
оси OХ
y=f(x) → y=f(kx), где k>0
(x0;y0) → ( x0;y0)
k
1
Для построения графика функции
y=f(kx) необходимо график функции
y=f(x) сжать в k раз вдоль оси ОХ для
k >1 или растянуть в 1/k раз вдоль
оси OХ для k<1

10. y=cosx y=cos2x y=cos(1/2x)

11. Симметричное отображение
относительно оси OY
y=f(x) → y=-f(x)
(x0;y0) → (x0;-y0)
Для построения
графика функции
y=-f(x) необходимо
график функции
y=f(x)симметрично
отобразить
относительно оси
ОХ

12. y=cosx y=-cosx

13. Симметричное отображение
относительно оси OХ
y=f(x) → y=f(-x)
(x0;y0) → (-x0;y0)
Для построения
графика функции
y=f(-x) необходимо
график функции
y=f(x) симметрично
отобразить
относительно
оси ОY

14. y=tgx y=tg(-x)

15. Построение графика y=|f(x)|
Для построения графика функции y=|f(x)|
необходимо часть графика функции
y=f(x), лежащую выше оси OX, оставить
неизменной, а часть графика y=f(x),
лежащую ниже оси OХ, симметрично
отобразить относительно оси ОХ
f(x), если х 0
y=|f(x)|=
-f(x), если х < 0{ ≥

16. X
Y
−2π −1π 1π 2π
−3
−2.5
−2
−1.5
−1
−0.5
0.5
1
1.5
2
2.5
3
0
xy sin=
xy sin=

17. Построение графика y=f(|x|)
f(x), если х 0
y=f(|x|)=
f(-x), если х<0
Для построения графика функции y=f(|
х|) необходимо часть графика функции
y=f(x), лежащую правее оси OY,
оставить неизменной, а часть
графика y=f(x), лежащую левее оси OY
“отбросить” и достроить график
симметрично относительно оси ОY
{ ≥

18. X
Y
−2π −1π 1π 2π
−3
−2.5
−2
−1.5
−1
−0.5
0.5
1
1.5
2
2.5
3
0
xy sin=
xy sin=