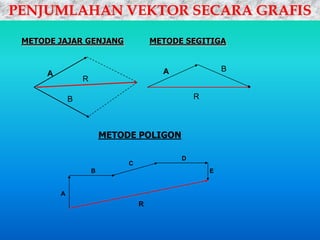
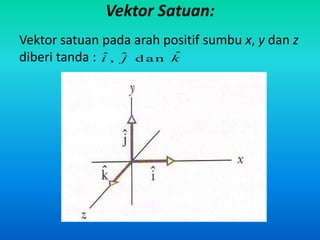
Dokumen ini menjelaskan konsep dasar vektor, termasuk besaran skalar dan vektor, serta metode penjumlahan dan pengurangan vektor. Juga dibahas perkalian vektor, baik skalar maupun silang, serta cara menentukan besar dan arah resultan antara dua vektor. Selain itu, terdapat contoh perhitungan yang merinci penggunaan rumus-rumus yang relevan.

1. Drs. Agus Purnomo
aguspurnomosite.blogspot.com

2. Pengenalan Vektor
 Besaran Skalar adalah :
Besaran yang hanya memiliki besar ( nilai ) saja
Ex. : panjang, massa, dan waktu
 Besaran Vektor adalah :
Besaran yang memiliki besar ( nilai ) dan juga arah
Ex. : gaya, kecepatan, dan percepatan
Penggambaran & Penulisan Vektor
Y Q Y Q
A B
P P
X X
Dua vektor yang sama posisi dan besarnya, tetapi arahnya berlawanan

3. P E N J U M L A H A N V E K T
O R
Jika vektor U ( a1, b1 ) dan vektor V ( a2, b2 ) adalah dua vektor pada
sebuah bidang datar, penjumlahan kedua vektor ini adalah U + V
U + V = ( a1 + a2, b1 + b2 )
Sedangkan pengurangan kedua vektor dapat dinyatakan sebagai
penjumlahan vektor U dengan vektor yang panjangnya sama dengan
V tetapi arahnya berlawanan
U - V = ( a1 - a2, b1 - b2 )
CONTOH
Jika U = ( 2, 6 ) dan V = ( -4, 8 ), tentukan U + V dan U – V
a. U + V = ( 2 + (-4), 6 + 8 ) = ( -2, 14 )
b. U – V = ( 2 – ( -4), 6 – 8 ) = ( 6, -2 )

4. PENJUMLAHAN VEKTOR SECARA GRAFIS
METODE JAJAR GENJANG METODE SEGITIGA
A B
A
R
B R
METODE POLIGON
D
C
B E
A
R

5. PENJUMLAHAN VEKTOR SECARA GRAFIS
  
s a b

6. • Komutatif :
   
a b b a

7. Assosiatif :
     
(a b) c a (b c)

8. Vektor b adalah vektor yang memiliki besaran
yang sama dengan vektor -b tetapi berlawanan
arah, bila dijumlahkan akan menghasilkan :
 
(b ) ( b) 0

9.  ax
Besar vektor a : a a
2
x
a
2
y
dan ta n
ay
 
Khusus untuk penjumlahan 2 vektor (
 ),
a dan b
besar vektor dapat dicari dengan rumus :
s
2 2
s a b 2 ab cos
Dalam perhitungan vektor dibutuhkan rumus trigonometri :
Dalil cosinus :
2 2 2
a b c 2 bc cos
2 2 2
b a c 2 ac cos
2 2 2
c a b 2 ab cos
Dalil sinus :
a b c
sin sin sin

10. Materi Pembelajaran
Jika vektor A dan B yang masing-masing
membentuk sudut θ dan β ingin dijumlahkan
secara analitik, maka dicari komponen
masing-masing vektor.
Ax = A cos θ ; Ay = A sin θ
Bx = B cos β ; By = B sin β

11. Materi Pembelajaran
Perkalian vektor dapat dilakukan
dengan dua metode, yaitu perkalian
Skalar dan perkalian silang.
Perkalian skalar vektor A dan vektor B
didefinisikan sebagai :
A . B = AB cos ө
Perkalian silang dua vektor didefinisikan sebagai :
A x B = AB sin ө

12.  
a .b ab cos

13. Dituliskan secara komponen bagian sebagai berikut :
 
a .b ( a cos )( b ) ( a )( b cos )
Scalar product berlaku hukum komutatif
   
a .b b .a
Jika ditulis dalam vektor satuan, maka perkalian scalar :
  ˆ ˆ ˆ
a .b (a xi ay ˆ
j ˆ
a z k ).( b x i by ˆ
j bz k )
Diperoleh hasil akhir sebagai berikut :
 
a .b a x bx a yby a z bz

14. Menghasilkan vector : Vector Product
Dikenal sebagai : Cross Product
  
a xb c
Dengan besar c adalah :
c ab sin
     
Besaran a x b ditulis a xb 0 jika a // b
 
dan maksimum jika a b

15. 
Arah dari vektor c tegak lurus bidang yang berisi vektor
 
a dan b dikenal sebagai hukum tangan kanan.
   
b xa (a x b )

16. Penulisan dalam vektor satuan :
  ˆ ˆ
a xb ( a x iˆ ay ˆ
j a z k ) x ( b x iˆ by ˆ
j bz k )
ˆ ˆ
a x i x bx i ˆ ˆ
a x b x (i x i ) 0
axi x by ˆ
ˆ j a x b y (i x ˆ )
ˆ j ˆ
a xby k
Hasil akhir :
 
axb ( a y b z b y a z )iˆ ( a z b x b z a x ) ˆ ( a x b y b x a y ) kˆ
j

17. Materi Pembelajaran
MENENTUKAN BESAR & ARAH RESULTAN DUA BUAH VEKTOR
2 2 2 2
RR F1F1 F F 2 F2 F 21 F 2 cos
2 1 F
2
cos
Besar / Nilai Resultan Dua Buah Vektor
R F2
sin sin
Arah Vektor

18. Materi Pembelajaran
MENENTUKAN BESAR & ARAH RESULTAN DUA BUAH VEKTOR
DENGAN MENGGUNAKAN VEKTOR KOMPOENEN
2 2
Fx F cos F FX FY FY F sin
Besar / Nilai Resultan Dua Buah Vektor
Fy
tan
Fx
Arah Vektor

19. Vektor Satuan:
Vektor satuan pada arah positif sumbu x, y dan z
ˆ
diberi tanda : i , ˆ d a n k
ˆ j

20.  
Kita dapat tulis vektor a dan b sebagai berikut :
 ˆ
a a xi ay ˆ
j
 disebut komponen vektor
b ˆ
bx i by ˆ
j

21. Materi Pembelajaran
CONTOH SOAL
1
Tentukan besar dan arah resultan dua buah
vektor perpindahan, jika diketahui vektor –
vektor komponennya sebagai berikut : Diketahui dua buah vektor
a. Ax = - 4 3 cm dan Ay = 4 cm kecepatan bergerak
b. Bx = 6 cm dan By = - 8 cm berlawanan arah dimana
vektor X besarnya 3 m/s
3 dan vektor Y besarnya 8 m/s
2 Tentukan nilai dan arah
Dua buah vektor gaya masing – masing resultan dua buah vektor
besarnya 4 N dan 5 N membentuk sudut apit kecepatan tersebut jika
sebesar 600. Tentukan besar / nilai resultan sudut apitnya 900 !
dua buah vektor gaya tersebut beserta
arahnya !

22. Terima
Kasih
Home SK & KD Materi Indikator Latihan RPP &
LKS

23. OK kawan....
Selamat Belajar ya
....
aguspurnomosite.blogspot.com