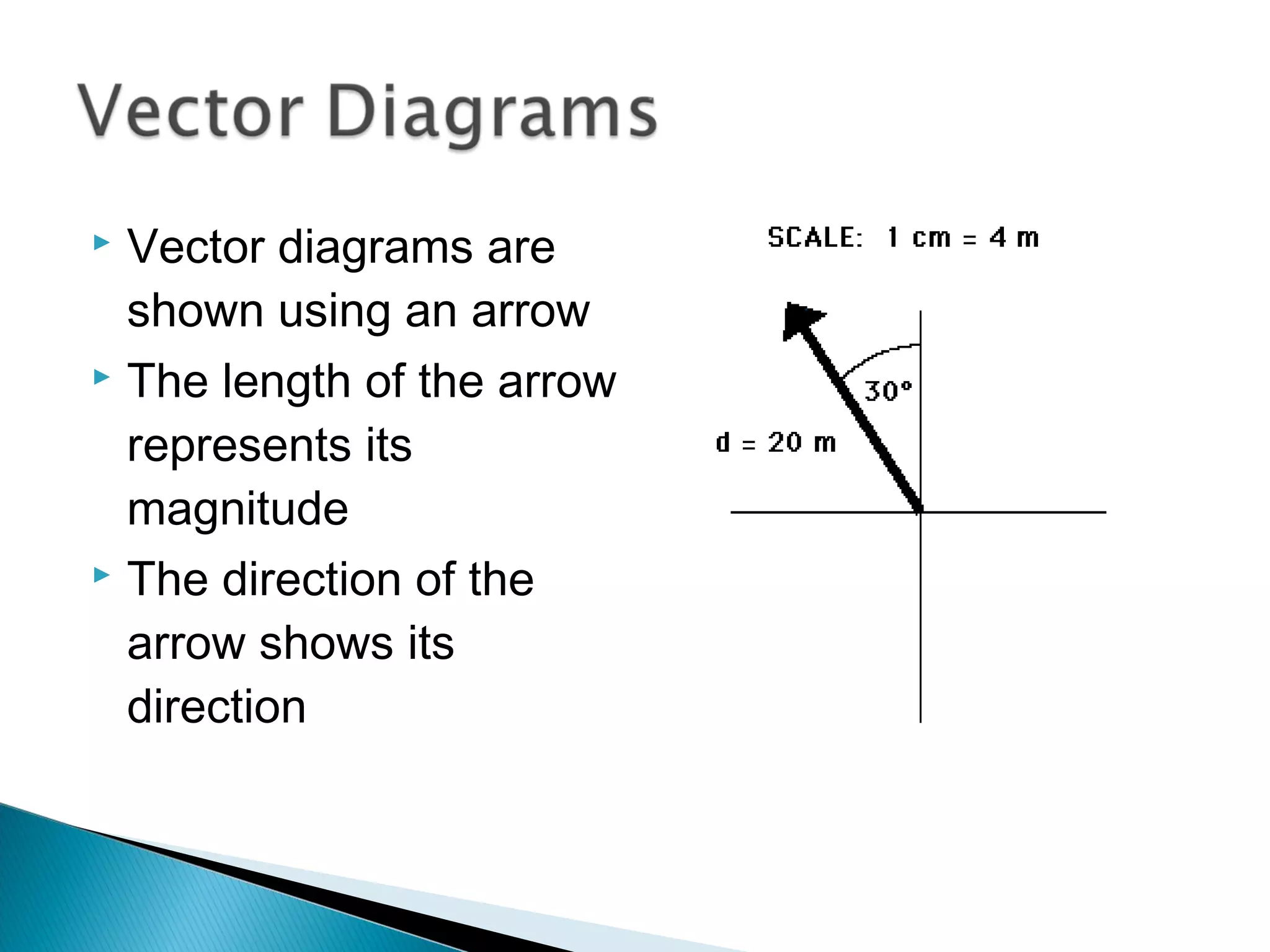
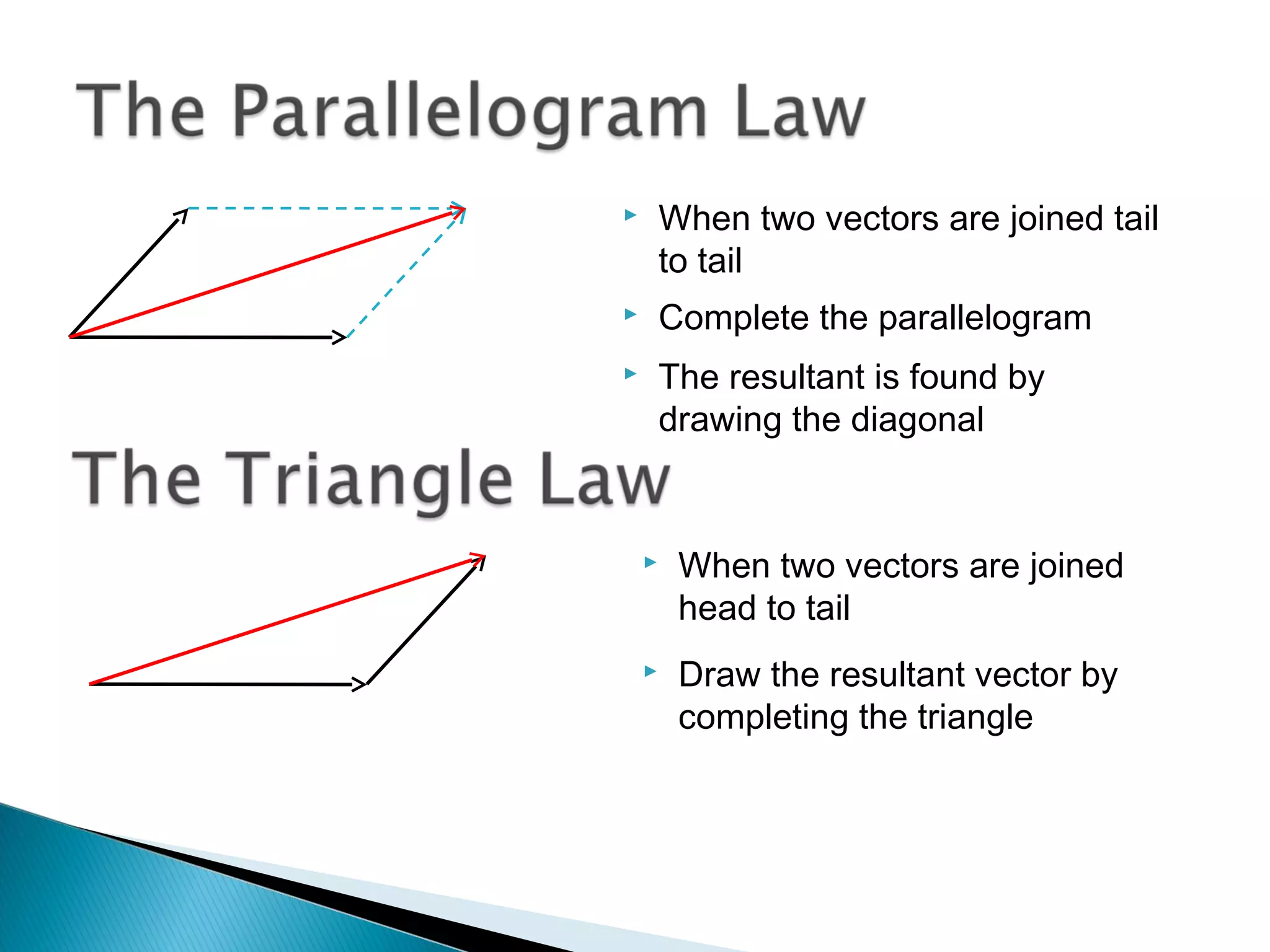
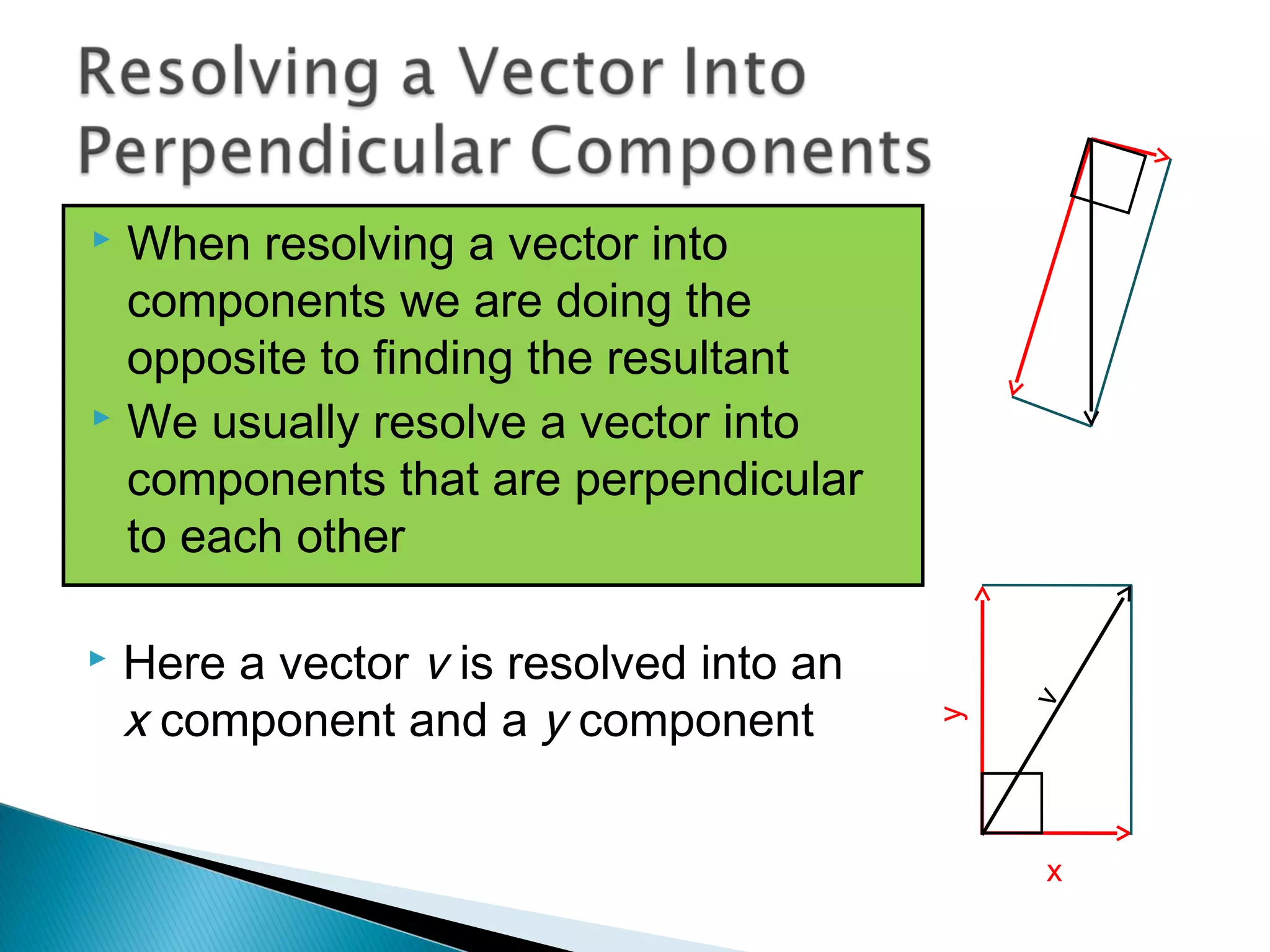
The document discusses scalar and vector quantities. It defines a scalar quantity as having only magnitude, and vector quantities as having both magnitude and direction. Length, time, and mass are provided as examples of scalars, while displacement, velocity, and force are examples of vectors. Vectors are represented using arrows with length indicating magnitude and direction indicating direction. The resultant of two vectors is found by combining them tail to tail using the parallelogram law or head to tail using the triangle law. Resolving vectors into perpendicular components and the relationships between magnitudes are also covered.

1. Copyright © John O’Connor
St. Farnan’s PPS
Prosperous
For non-commercial purposes only….. Enjoy!
Vectors and Scalars
Comments/suggestions please to the SLSS physics website forum
@ http://physics.slss.ie/forum

2.  A scalar quantity is a quantity that has magnitude
only and has no direction in space
Examples of Scalar Quantities:
 Length
 Area
 Volume
 Time
 Mass

3.  A vector quantity is a quantity that has both
magnitude and a direction in space
Examples of Vector Quantities:
 Displacement
 Velocity
 Acceleration
 Force

4.  Vector diagrams are
shown using an arrow
 The length of the arrow
represents its
magnitude
 The direction of the
arrow shows its
direction

5. Vectors in opposite directions:
6 m s-1
10 m s-1
= 4 m s-1
6 N 10 N = 4 N
Vectors in the same direction:
6 N 4 N = 10 N
6 m
= 10 m
4 m
 The resultant is the sum or the combined effect of
two vector quantities

6.  When two vectors are joined tail
to tail
 Complete the parallelogram
 The resultant is found by
drawing the diagonal
 When two vectors are joined
head to tail
 Draw the resultant vector by
completing the triangle

7. Solution:
 Complete the parallelogram (rectangle)
θ
 The diagonal of the parallelogram ac represents the
resultant force
2004 HL Section B Q5 (a)
Two forces are applied to a body, as shown. What is the
magnitude and direction of the resultant force acting on the
body?
5N
12 N
5
12
a
b c
d
 The magnitude of the resultant is found using
Pythagoras’ Theorem on the triangle abc
N13
512Magnitude 22
=
+==
ac
ac
°==⇒
=
−
67
5
12
tan
5
12
tan:ofDirection
1
θ
θac
 Resultant displacement is 13 N 67º
with the 5 N force
13 N

8. 45º
5 N
90ºθ
Find the magnitude (correct to two decimal places) and direction
of the
resultant of the three forces shown below.
5N
5
5
Solution:
 Find the resultant of the two 5 N forces first (do right angles first)
a b
cd
N07.75055 22
==+=ac
°=⇒== 451
5
5
tan θθ
7.07
N
10
N
135º
 Now find the resultant of the 10 N and 7.07
N forces
 The 2 forces are in a straight line (45º + 135º
= 180º) and in opposite directions
 So, Resultant = 10 N – 7.07 N = 2.93 N in
the direction of the 10 N force
2.93
N

9.  What is a scalar quantity?
 Give 2 examples
 What is a vector quantity?
 Give 2 examples
 How are vectors represented?
 What is the resultant of 2 vector quantities?
 What is the triangle law?
 What is the parallelogram law?

10.  When resolving a vector into
components we are doing the
opposite to finding the resultant
 We usually resolve a vector into
components that are perpendicular
to each other
y
v
x
 Here a vector v is resolved into an
x component and a y component

11.  Here we see a table
being pulled by a force of
50 N at a 30º angle to the
horizontal
 When resolved we see
that this is the same as
pulling the table up with a
force of 25 N and pulling
it horizontally with a force
of 43.3 N
50 Ny=25 N
x=43.3 N
30º
 We can see that it
would be more
efficient to pull the
table with a horizontal
force of 50 N

12.  If a vector of magnitude v and makes an angle θ with the
horizontal then the magnitude of the components are:
 x = v Cos θ
 y = v Sin θ
v
y=v Sin θ
x=v Cos θ
θ
y
 Proof:
v
x
Cos =θ
θvCosx =
v
y
Sin =θ
θvSiny =
x

13. 60º
2002 HL Sample Paper Section B Q5 (a)
A force of 15 N acts on a box as shown. What is the horizontal
component of the force?
Vertical
Component
Horizontal
Component
Solution:
N5.76015ComponentHorizontal =°== Cosx
N99.126015ComponentVertical =°== Siny
15N
7.5 N
12.99N

14.  A person in a wheelchair is moving up a ramp at constant speed.
Their total weight is 900 N. The ramp makes an angle of 10º with
the horizontal. Calculate the force required to keep the wheelchair
moving at constant speed up the ramp. (You may ignore the
effects of friction).
Solution:
If the wheelchair is moving at constant speed (no acceleration), then the force
that moves it up the ramp must be the same as the component of it’s weight
parallel to the ramp.
10º
10º80º
900 N
Complete the parallelogram.
Component of weight
parallel to ramp:
N28.15610900 =°= Sin
Component of weight
perpendicular to ramp:
N33.88610900 =°= Cos
156.28 N
886.33 N
2003 HL Section B Q6

15.  If a vector of magnitude v has two perpendicular
components x and y, and v makes and angle θ
with the x component then the magnitude of the
components are:
 x= v Cos θ
 y= v Sin θ
v
y=v Sin θ
x=v Cosθ
θ
y