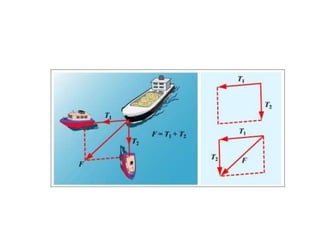
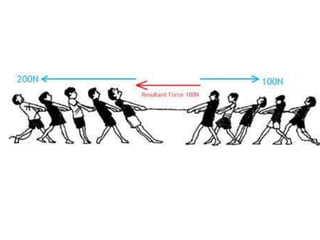
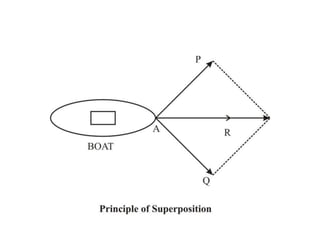
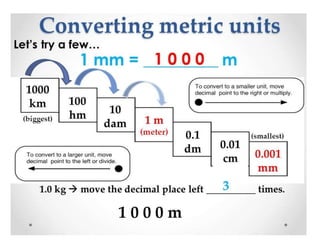
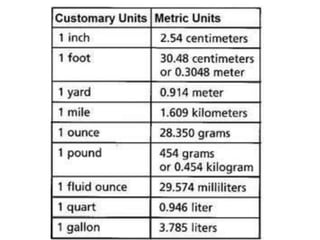
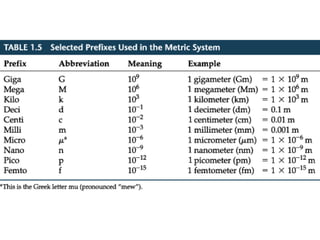
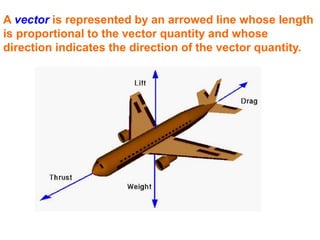
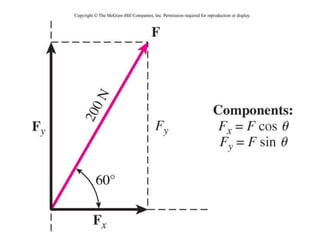
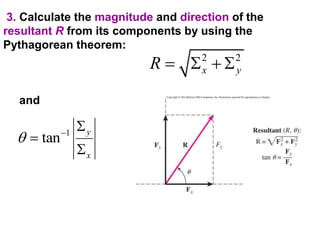
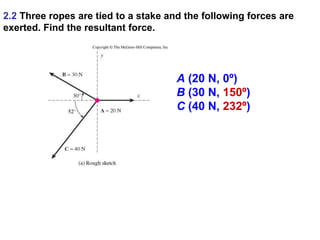
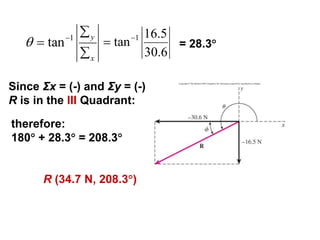
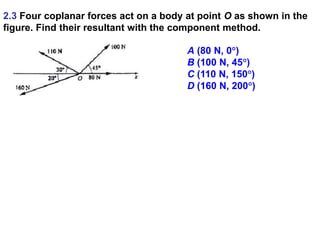
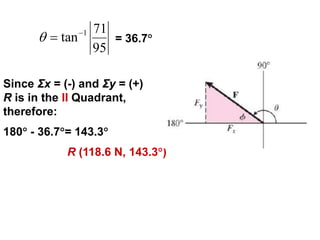
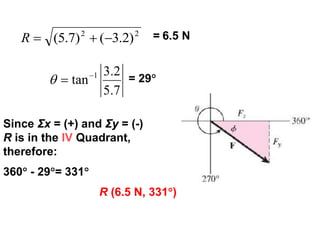
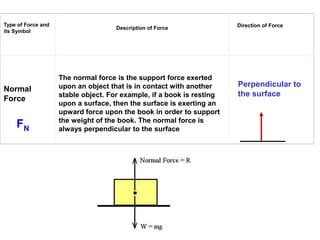
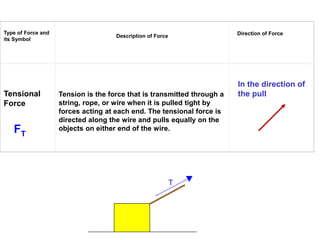
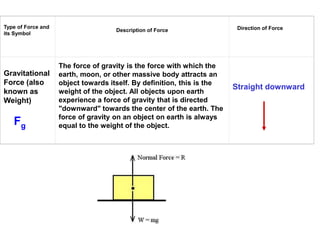
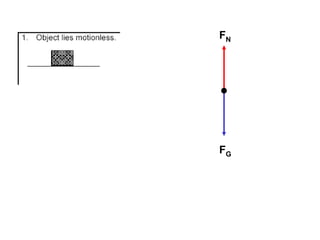
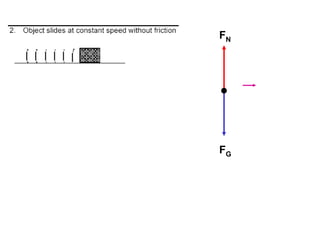
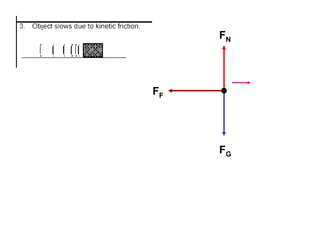
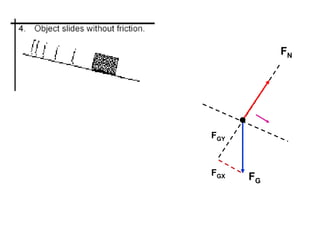
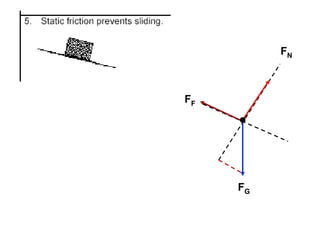
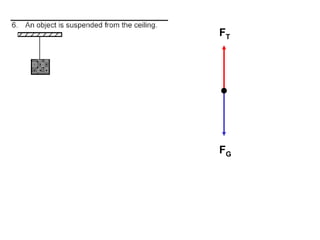
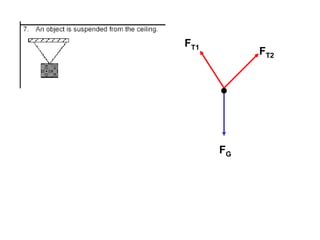
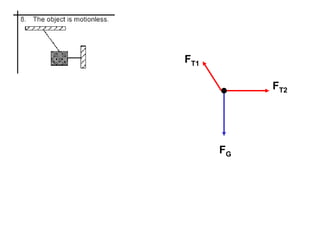
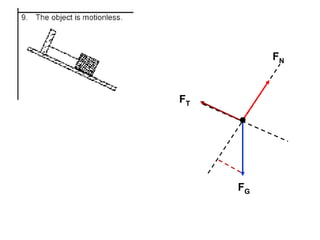
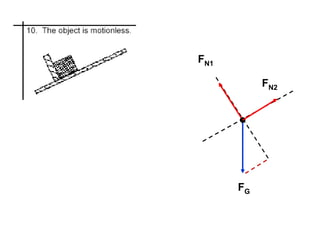
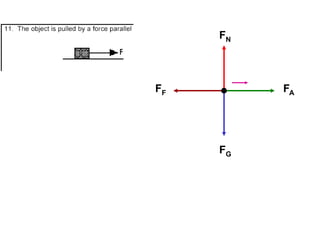
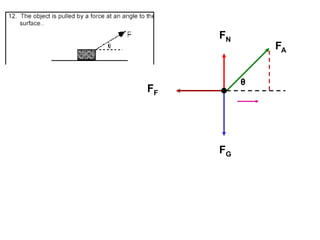
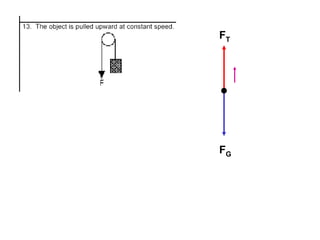
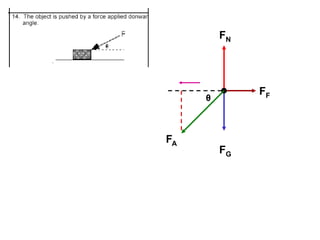
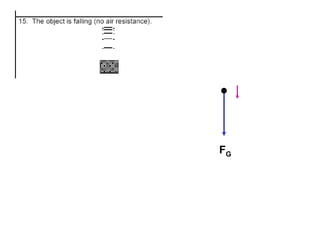
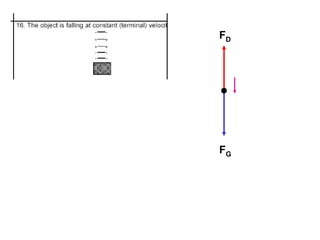
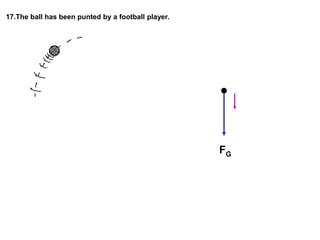
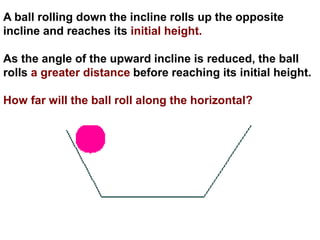
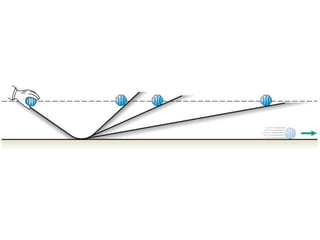
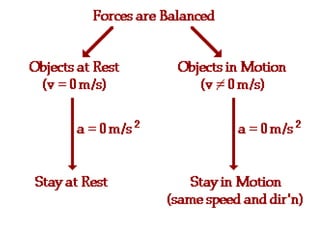
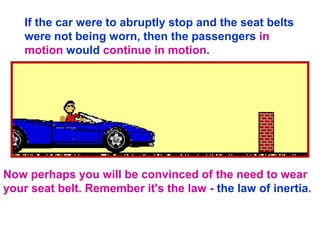
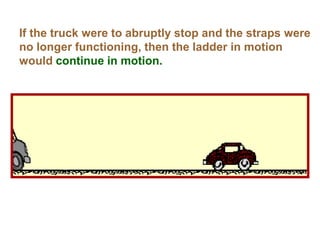
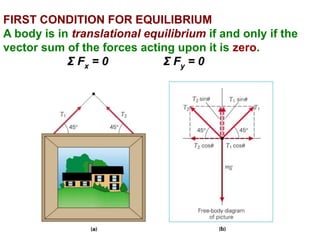
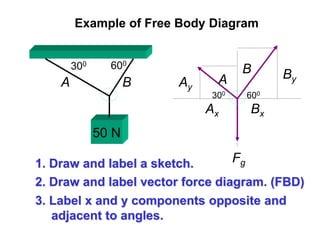
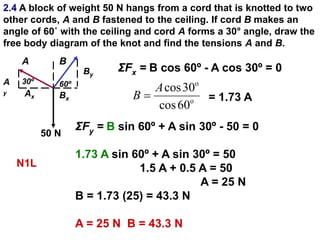
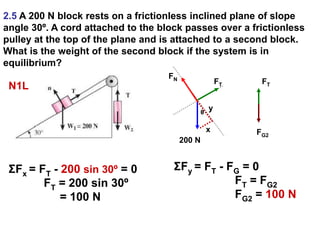
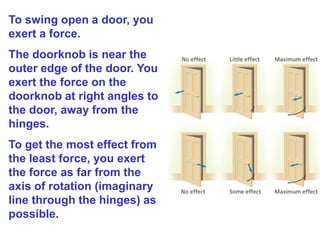
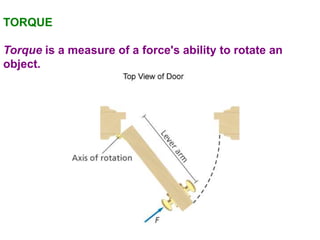
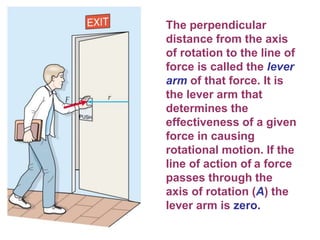
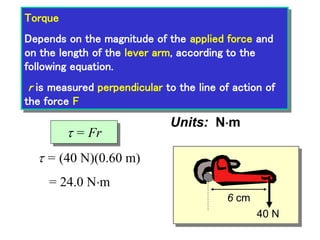
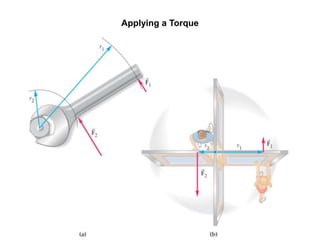
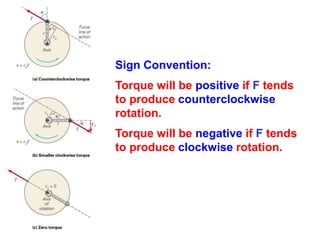
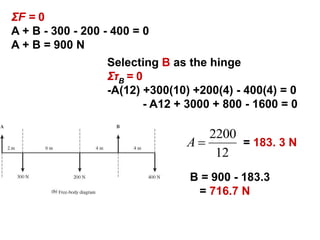
1. A resultant force is a single force that has the same effect on a rigid body as the original system of forces acting on it. It is obtained by combining all the individual forces.
2. The principle of superposition states that the combined effect of multiple forces acting on an object is equal to the sum of the effects of each individual force.
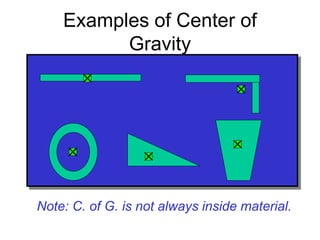
3. A rigid body is an idealization in which deformation is neglected, meaning the distances between any two points remain constant regardless of external forces.