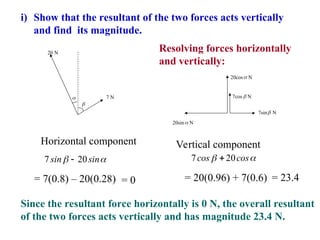
The document discusses the combination and resolution of forces into their components and finding the resultant force using various examples. It includes calculations for horizontal and vertical components, along with the application of trigonometric functions to determine the resultant force's magnitude and direction. The document also features scenarios involving multiple forces acting at a point and addresses specific cases to illustrate the principles of force resolution.

1. Components or resolved forces
We have seen that two forces can be combined into a
single force which is called their resultant.
There is the reverse process which consists of expressing
a single force in terms of its components. These
components are sometimes referred to as the resolved
parts of the force.
F
x
y

O X
Y
OX = F cos 
OY = F sin 
Learning objectives
Splitting forces into their components
Finding the resultant of two or more forces

2. Example
30
Y
X
20 N
30°
20 N
X = 20 x Cos 30 = 17.3 N
Y = 20 x Sin 30 = 10.0 N

3. More examples
X = -15  Cos 42 = -11.1 N
Y = 15  Sin 42 = 10.0 N
X = 35  Cos 62
=
16.4 N
Y = -35  Sin 62 = - 30.9 N
x
y
42°
15 N
x
y
62°
35 N
x
y
32°
10 N
X = -10  Sin 32
=
- 5.30 N
Y = -10  Cos 32 = -8.48 N

4. Finding the resultant of two forces
using the component method
30°
8 N
5 N
X = 8 + 5 x Cos 30 = 12.33 N
Y = 5 x Sin 30 = 2.5 N
12.33

2.5 N
Resultant
Resultant = 2
2
5
.
2
33
.
12  = 12.6 N
8 N 5cos30
5sin30
30°
  tan -1
(2.5/12.33)  11.5

5. Draw a force diagram
and, where appropriate,
redraw each force into
any two perpendicular
directions.
Find the resultant
in each direction.
Find the resultant of the following forces:
2 N
6 N
30°
2 N
6 N
30°
6 cos 30° N
6 sin 30° N
2 N
Horizontal component
X = 6 cos 30° + 2
= 7.196…
Vertical component
Y = 6 sin 30°
= 3
Find the overall
resultant.
2
2
3
...
19
.
7 

F
= 7.79… 7.1… N
3 N F N
The resultant force has magnitude 7.8 N (2 s.f.)

6. Find the resultant of the following forces:
10 N
4 N
120°
Draw a force diagram
and, where appropriate,
redraw each force
resolved into any two
perpendicular directions. 10 N
4 N
120°
60°
4 sin 60° N
10 N
4 cos 60° N
Find the resultant
in each direction.
Find the
overall resultant.
Horizontal component
X = 10 – 4 cos 60°
= 8
Vertical component
Y = 4 sin 60°
= 3.46…
2
2
8
...
46
.
3 

F
= 8.71…
The resultant force has magnitude 8.7 N (2 s.f.)
8 N
3.46… N F N

7. More than two forces
2
2
Y
X 
 Split each force into components in these directions.
 Choose two directions at right angles to each other.
 For each direction, find the sum of the components.
 Find the resultant.
 Find the required angle.
 Pythagoras: R 
 Angle with the X direction  = 






X
Y
1
tan

8. Example
2
2
Y
X 
x
y
20 N
70°
12 N
8 N
30°
Force X Y
20 N 20 cos 70 = 6.8404 20 sin 70 = 18.7939
12 N 12.0000 0
8 N -8 cos 30 =- 6.9282 -8 sin 30 = - 4.0000
Total 11.9122 14.7939

Resultant
R =
R = 19.0 N
 = 






X
Y
1
tan
 = 51.2°

9. Example
x
y
6 N
30 N
50°
20 N
35°
5 N
X = 20 cos 35 – 30 sin 50 – 5 = - 11.5983
Y = 6 – 20 sin 35 – 30 cos 50 = - 24.7552
 2
2
Y
X 
R = = 27.3 N
 = 






X
Y
1
tan = 64.9°

10. More example
Two forces act at a point. The magnitude of the forces are 3.95 N and
2.5 N, and angle between their direction is 90 + , where 0 << 90. The
resultant of the two forces has magnitude R N and its line of action
makes an angle of 90 with the force of magnitude 2.5 N, as shown in
the diagram. Find the value of R and .
R N
2.5 N
Resolving 
3.95 N

3.95 sin  = 2.5 : sin  = 2.5/3.95 : Giving  = 39.3°
Resolving  R = 3.95 x cos 39.3 = 3.06 N

11. Three forces, of magnitudes 8 N, 10 N, and 8 N, act at a point P in
the direction shown in the diagram. PQ is the bisector of the
acute angle between the two forces of magnitude 8 N.
Find
(i) the components of the resultant of the three forces a parallel to
PQ
(a) parallel to PQ
(b) perpendicular to PQ
(ii) the magnitude of the resultant of the three forces,
(iii) the angle that the resultant of the three forces makes with PQ.
8 N
8 N
10 N
P
Q
40°
40°
130°
150°

12. Resolving forces horizontally
and vertically:
10cos 10° N
10sin 10° N 8sin 40° N
8cos 40° N
8cos 40° N
8sin 40° N
8 N
8 N
10 N
P
Q
40°
40°
130°
10°
i) the components of the resultant of the three forces
(a) parallel to PQ
Horizontal component X = 8 cos 40° + 8 cos 40° – 10 cos 10°
= 2.4086…= 2.41 N (3 s.f.)
Vertical component Y = 10 sin 10° + 8 sin 40° – 8 sin 40°
= 1.7364…= 1.74 N (3 s.f.)
(b) perpendicular to PQ

13. ii) the magnitude of the resultant of the three forces,
2 2
F X Y
 
2
2
...
73
.
1
...
40
.
2 

= 2.9693…
The resultant force has magnitude 2.97 N (3 s.f.)
iii) the angle that the resultant of the three forces makes
with PQ.
...
40
.
2
...
73
.
1
tan 


The angle that the resultant makes with PQ is 35.8° (1 d.p.)
...
789
.
35




14. Two forces act in a vertical plane. The forces have
magnitudes 20 N and 7 N and make angles and respectively
with the upward vertical, as shown in the diagram. The
angles and are such that cos ≈ 0.96 and cos ≈ 0.6. [You are
given that sin ≈ 0.28 and sin ≈ 0.8.]
i) Show that the resultant of the two forces acts vertically and
find its magnitude.
ii) The two forces act on a particle of mass 2.5 kg. State, giving a
reason, whether the direction of the acceleration of the
particle is vertically upwards or downwards.
20 N
7 N



15. Resolving forces horizontally
and vertically:
20 N
7 N


7cos N
20sin N
7sin N
20cos N




i) Show that the resultant of the two forces acts vertically
and find its magnitude.
Horizontal component
= 7(0.8) – 20(0.28) = 0
Vertical component
= 20(0.96) + 7(0.6) = 23.4
7 20
sin sin
 
 7 20
cos cos
 

Since the resultant force horizontally is 0 N, the overall resultant
of the two forces acts vertically and has magnitude 23.4 N.

16. (ii) The two forces act on a particle of mass 2.5 kg. State, giving a
reason, whether the direction of the acceleration of the particle is
vertically upwards or downwards.
23.4 N
2.5g N = 24.5 N
Since the weight is greater than the upward force (the resultant
force), the direction of the acceleration is vertically downwards.