Download to read offline
Uploaded byNirmal Rizal
Vector and scalar
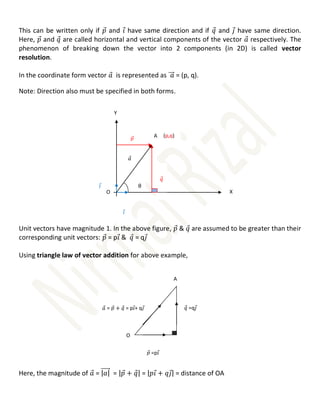
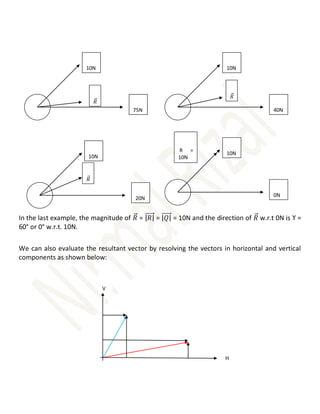
The document explains the fundamental concepts of scalar and vector quantities, including their definitions, representations, and operations. It covers examples of calculating distances, displacements, and resultant forces through vector addition and resolution, underscoring the importance of direction in vector analysis. The document also discusses the relationship between different vector quantities and how to derive scalar products.
More Related Content
![Motion In a Plane LNN [Lecture Note].pdf](https://cdn.slidesharecdn.com/ss_thumbnails/motioninaplanelecturenote-250429154348-b30844fd-thumbnail.jpg?width=640&height=640&fit=bounds)
![Polymer [ बहुलक ] Chemistry Notes PDF - Irfanullah Mehar - JJ Sir Chemistry.pdf](https://cdn.slidesharecdn.com/ss_thumbnails/polymerchemistrynotespdf-irfanullahmehar-jjsirchemistry-260210172118-3f9b37f7-thumbnail.jpg?width=640&height=640&fit=bounds)
Vector and scalar
- 1. Introduction to scalarand vector Let us begin with the following questions: a. You are at rest position and an object is moving at a speed of 10km/hr. What would be the distance (gap) between you and the object after 30 minutes? It is pretty simple. The distance will be 5 km. b. You are moving to the opposite of an object at a speed of 20 km/hr. The object is moving at a speed of 10km/hr in the North. (i) What would be the distance covered by you in 30 minutes? (ii) What would be the distance (gap) between you and the object in 30 minutes? (iii) What would be the displacement of the object in 30 minutes? (iv) What would be the displacement of the object w.r.t the origin in 15 minutes? (i) It is 10 km. (ii) In 30 minutes, you will cover a distance of 10 km (in the South) and the object will cover a distance of 5 km (in the North). So, a gap of 15 km will be made. (iii) Actually, the question is not precise. It should have been asked in this fashion, 'What would be the displacement of the object w.r.t you after 30 minutes'? The displacement w.r.t you will be 15 km in the case. (iv) It is 2.5 km to the North of the origin. (Note: displacement is a vector & direction must be specified for vectors) Q. How are magnitude and direction imparted to a vector quantity? Magnitude and direction are imparted on the Cartesian plane. To impart the magnitude, a reference point or an initial point is required as the magnitude is the distance between two points. While, to impart the direction, a line is required that passes through the reference point. It will become clear from the following diagram:
- 2. The magnitude of𝑎 ⃗ = |𝑎| ⃗⃗⃗⃗⃗⃗ = OA. OA can be evaluated if the coordinates of O and A are Known. If O = (0,0) and A = (a,b), OA = √𝑎2 + 𝑏2. It is not mandatory that the direction (θ) must be always about the horizontal line or x-axis. It can be about any line. But the line must be specified. For example, a ball is moving at a velocity of 5km/hr in the North or in the N45E. Here the line is specified. N45E is 45° about the North in clockwise direction. Here the line is specified as the North. So now on, we must be able to decide that the vector 𝑎 ⃗ has the magnitude |𝑎| ⃗⃗⃗⃗⃗⃗ and it is directed somewhere. Q. Look at the diagram, there are two vectors equal in magnitude. Are the vectors equal? No. Not only magnitude but also the direction of two vectors must be same in order tobe equal. Representation of vectors & resolution of vectors Vectors can be represented in the coordinate form (p,q) and in the form of unit vectors. If 𝑖 ⃗ and 𝑗 ⃗ are unit vectors along x-axis and y-axis respectively, 𝑝 ⃗ = p𝑖 ⃗ & 𝑞 ⃗ = q𝑗 ⃗ θ O A X Y 𝑎 ⃗ o
- 3. This can bewritten only if 𝑝 ⃗ and 𝑖 ⃗ have same direction and if 𝑞 ⃗ and 𝑗 ⃗ have same direction. Here, 𝑝 ⃗ and 𝑞 ⃗ are called horizontal and vertical components of the vector 𝑎 ⃗ respectively. The phenomenon of breaking down the vector into 2 components (in 2D) is called vector resolution. In the coordinate form vector 𝑎 ⃗ is represented as 𝑎 ⃗⃗⃗⃗ = (p, q). Note: Direction also must be specified in both forms. Unit vectors have magnitude 1. In the above figure, 𝑝 ⃗ & 𝑞 ⃗ are assumed to be greater than their corresponding unit vectors: 𝑝 ⃗ = p𝑖 ⃗ & 𝑞 ⃗ = q𝑗 ⃗ Using triangle law of vector addition for above example, Here, the magnitude of 𝑎 ⃗ = |𝑎| ⃗⃗⃗⃗⃗⃗ = |𝑝 ⃗ + 𝑞 ⃗| = |𝑝𝑖 ⃗ + 𝑞𝑗 ⃗| = distance of OA 𝑖 ⃗ (p,q) θ O A X Y 𝑎 ⃗ 𝑝 ⃗ 𝑞 ⃗ 𝑖 ⃗ 𝑗 ⃗ 𝑝 ⃗ =p𝑖 ⃗ 𝑞 ⃗ =q𝑗 ⃗ 𝑎 ⃗ = 𝑝 ⃗ + 𝑞 ⃗ = p𝑖 ⃗+ q𝑗 ⃗ O A
- 4. From above, wecan infer that a vector (p, q) = 𝒑𝒊 ⃗ + 𝒒𝒋 ⃗ has: a horizontal component = 𝒑 ⃗⃗⃗⃗ = 𝒑𝒊 ⃗ and a vertical component = 𝒒 ⃗⃗⃗⃗ = 𝒒𝒋 ⃗ Or, we can say that a vector is equal to the summation of it's components. Q. Can the resultant of two different vector quantities (example force and velocity) be evaluated? No. We cannot decide whether the resultant (𝑅 ⃗⃗) would be force (𝐹 ⃗) or velocity ( 𝑉 ⃗⃗) or any other quantity. Q. Give a justification for the statement 'Both the horizontal and vertical components of a vector are vectors'. Directions of the components of a vector can be identified w.r.t the vector itself or w.r.t the x- axis or w.r.t the y-axis. Q. How would a vector origin? A vector gets originated due to: The resultant of 2 vectors A single vector Cross/vector product between 2 vectors Let us have a look on the diagram that shows the distribution of forces at 4 different points outside the bounded region. An object of mass 0.5 kg is inside the bounded region and exerting equal force (5N) opposite to the forces as shown below: 𝐹 ⃗ 𝑉 ⃗⃗ 𝑅 ⃗⃗
- 5. At all thepoints, the mass of the object will remain unchanged as mass being scalar quantity is not affected by direction. But the resultant force at all the points will remain changed. Resultant of vectors 1. Imagine a ball is being pulled with two forces in opposite directions. Where would the ball go? The ball will move to the right side since the net force or the resultant of two forces is directed along the right side. The net/resultant force = 75-10 = 65N and the direction is along the direction of P. 2N 4N 6N 8N 5N 5N 5N 5N 𝑄 ⃗⃗ = 10N 𝑃 ⃗⃗ = 75N
- 6. 2. Imagine aball is being pulled with two forces in same direction. Where would the ball go? The ball will move to the right side since the net force or the resultant of two forces is directed along the right side. The net/resultant force = 75+10 = 85N and the direction is along the direction of P. In the problem 1: the angle between two forces is 180° and the resultant force is directed along the greater force. And, the magnitude of the resultant force = greater force-smaller force. In the problem 2: the angle between two forces is 0° and the resultant force is directed along the given forces. And, the magnitude of the resultant force = greater force + smaller force. 3. Imagine a ball is being pulled with two forces in different directions. Where would the ball go? To answer this we need to observe the previous problems. From those problems we can infer that the magnitude and the direction of the resultant force depend on: the angle between two forces and the magnitude of the forces. 75N 10N 10N 75N
- 7. 4. What wouldbe the direction of the resultant force? Just think of intuitive answer. The direction of the resultant force is always closer to the greater force and farther from the smaller force as the impact of the greater force is greater than that of the smaller force. The ball neither moves along 10N nor along 75N. Hence the ball moves midway between two forces being closer to the 75 N. 5. What would be the magnitude of the resultant force (𝑅 ⃗⃗) if θ = 60°? The resultant force (𝑅 ⃗⃗) will be such that R2 = |𝑃| ⃗⃗⃗⃗⃗⃗2 +|𝑄| ⃗⃗⃗⃗⃗⃗2 +2|𝑃| ⃗⃗⃗⃗⃗⃗|𝑄| ⃗⃗⃗⃗⃗⃗Cosθ where: 𝑃 ⃗⃗ and 𝑄 ⃗⃗ are two forces θ is the angle between two forces |𝑃| ⃗⃗⃗⃗⃗⃗ & |𝑄| ⃗⃗⃗⃗⃗⃗ are the magnitudes of 𝑃 ⃗⃗ & 𝑄 ⃗⃗ respectively. In this example, 𝑃 ⃗⃗ = 75𝑁 ⃗⃗⃗⃗⃗⃗⃗⃗⃗, 𝑄 ⃗⃗ = 10𝑁 ⃗⃗⃗⃗⃗⃗⃗⃗⃗, θ = 60° R2 = |75| ⃗⃗⃗⃗⃗⃗⃗⃗⃗2 +|10| ⃗⃗⃗⃗⃗⃗⃗⃗⃗2 +2|75| ⃗⃗⃗⃗⃗⃗⃗⃗⃗|10| ⃗⃗⃗⃗⃗⃗⃗⃗⃗Cos60 = 100+5625+2.10.75.0.5 = 5725+750= 6475 N2 θ 10N 75N 𝑅 ⃗⃗
- 8. Thus, 𝑅 ⃗⃗ =√6475 N = 80.46 N Since, the force is a vector quantity it must have direction too. Let ϒ be the angle between 𝑅 ⃗⃗ & 75𝑁 ⃗⃗⃗⃗⃗⃗⃗⃗⃗. Then ϒ will be the direction of 𝑅 ⃗⃗ w.r.t. the line of 75𝑁 ⃗⃗⃗⃗⃗⃗⃗⃗⃗. We can assign the direction for 𝑅 ⃗⃗ w.r.t. 10𝑁 ⃗⃗⃗⃗⃗⃗⃗⃗⃗ too. The direction of 𝑅 ⃗⃗ is such that: tan ϒ = QSin θ/(P+QCos θ) In this example, tan ϒ = 10.Sin60/(75+10.Cos60) or, tan ϒ = 8.66/80, or ϒ = 𝑡𝑎𝑛−1 (8.66/80) = 6°. Meaning, 𝑅 ⃗⃗ & 75𝑁 ⃗⃗⃗⃗⃗⃗⃗⃗⃗are at a gap of 6° while, 𝑅 ⃗⃗ & 10𝑁 ⃗⃗⃗⃗⃗⃗⃗⃗⃗are at a gap of 54°. It shows that the impact of 75𝑁 ⃗⃗⃗⃗⃗⃗⃗⃗⃗ is higher on the ball. 6. What would happen if θ = 80° instead of 60°in example 5? The angular gap of two vectors is greater for θ = 80°. Whatever the angular gap is, similar phenomenon occurs. Meaning, the greater force will have greater impact on the ball and the smaller force will have smaller impact. θ = 80° will occur if 10 N further rotates towards N in anticlockwise. During rotation of 10 N (to maintain θ = 80°), the resultant will get pulled a bit towards 10 N. This will lead in increasing of the value ϒ = 6°. 7. Let us decrease the value of 𝑃 ⃗⃗ progressively until 𝑃 ⃗⃗ becomes 0 keeping 𝑄 ⃗⃗ and θ unchanged. What would happen to 𝑅 ⃗⃗? The magnitude and direction of 𝑅 ⃗⃗ also changes progressively. Ultimately, 𝑅 ⃗⃗ becomes 𝑄 ⃗⃗ as there will be no 𝑃 ⃗⃗ to impart impact on the ball.
- 9. In the lastexample, the magnitude of 𝑅 ⃗⃗ = |𝑅| ⃗⃗⃗⃗⃗⃗ = |𝑄| ⃗⃗⃗⃗⃗⃗ = 10N and the direction of 𝑅 ⃗⃗ w.r.t 0N is ϒ = 60° or 0° w.r.t. 10N. We can also evaluate the resultant vector by resolving the vectors in horizontal and vertical components as shown below: 10N 75N 𝑅 ⃗⃗ 10N 40N 𝑅 ⃗⃗ 10N 20N 𝑅 ⃗⃗ 10N 0N R = 10N H V
- 10. There are twovectors denoted by blue and red line arrows. Both have horizontal and vertical components. Just add the horizontal component of one vector to the horizontal component of another vector. Do similar in case of their vertical components. The two components will be formed. The angle between these newly formed components will be 90°. Just put these components in the formula of resultant vector. Note: To study the net impact of 2 vectors on a body, the resultant of two vectors is necessary to identify. The magnitude and direction of the resultant vector are to be evaluated. The calculation of the magnitude is different to that of the scalar quantities. Dot product and vector product (i) Derivation of dot/scalar product between two vectors in 2D Let 𝒂 ⃗ ⃗⃗ and 𝒃 ⃗ ⃗⃗ be two vectors with the origin 'o' as the common reference or initial point. Let θ2 and θ1 be their corresponding directions as show in the figure. Let θ2 be greater than θ1 for instance. Hence, the angle between the vectors = θ2 – θ1 = θ. Points P and Q have been projected onto the x-axis normally. Thus, the two right angled triangles, ∆OPM and ∆OQN get developed. From ∆OPM and ∆OQN,
- 11. Cosθ2 = m/OP= m/√𝒎𝟐 + 𝒑𝟐 = m/|𝒂 ⃗ ⃗⃗|……………………….……..1 Cosθ1 = n/OQ = n/√𝒏𝟐 + 𝒒𝟐 = n/|𝒃 ⃗ ⃗⃗|……………………..………………..….2 Sinθ2 = p/OP = p/√𝒎𝟐 + 𝒑𝟐 = p/|𝒂 ⃗ ⃗⃗|………………………………….3 Sinθ1 = q/OQ = q/√𝒏𝟐 + 𝒒𝟐 = q/|𝒃 ⃗ ⃗⃗|………………………….….…4 Taking Cos to both sides of the expression θ2 – θ1 = θ, Cos θ = Cos (θ2 – θ1) = Cos θ2 Cos θ1+ Sin θ2Sinθ1………………….…….5 From 1, 2, 3, 4 & 5, mn+pq = |𝒂 ⃗ ⃗⃗||𝒃 ⃗ ⃗⃗| Cosθ…………………………….……..6 Let 𝒊 ⃗ and 𝒋 ⃗ be two unit vectors along x-axis and y-axis respectively. Vectors can be represented in the form of unit vectors as: 𝒂 ⃗ ⃗⃗ = (m, p) = m𝒊 ⃗+p𝒋 ⃗ =𝒎 ⃗⃗⃗⃗+𝒑 ⃗ ⃗⃗………………………………………………………….7 𝒃 ⃗ ⃗⃗ = (n, q) = n𝒊 ⃗+q𝒋 ⃗ ⃗⃗ = 𝒏 ⃗⃗⃗+𝒒 ⃗ ⃗⃗…………………………………………..………………8 From 7 & 8, m𝒊 ⃗ = 𝒎 ⃗⃗⃗⃗, n𝒊 ⃗ = 𝒏 ⃗⃗⃗, p𝒋 ⃗ = 𝒑 ⃗ ⃗⃗ and q𝒋 ⃗ ⃗⃗ =𝒒 ⃗ ⃗⃗ ……………………………..………………9 Multiplying 7 and 8, 𝒂 ⃗ ⃗⃗ .𝒃 ⃗ ⃗⃗ = (m𝒊 ⃗+p𝒋 ⃗) . (n𝒊 ⃗+q𝒋 ⃗ ⃗⃗) 𝒂 ⃗ ⃗⃗ .𝒃 ⃗ ⃗⃗ = mn (𝒊 ⃗ .𝒊 ⃗ ) + mq (𝒊 ⃗ .𝒋 ⃗ ) + pn (𝒋 ⃗ .𝒊 ⃗ ) + pq (𝒋 ⃗ .𝒋 ⃗ )…………….………..10 For, 𝒊 ⃗ .𝒊 ⃗ = 𝒋 ⃗ .𝒋 ⃗ = 𝟏 and 𝒊 ⃗ .𝒋 ⃗ = 𝒋 ⃗ .𝒊 ⃗ = 0 equation 10 becomes, 𝒂 ⃗ ⃗⃗ .𝒃 ⃗ ⃗⃗ = mn + pq………………………………………………………………… ……11 From 11 & 6, 𝒂 ⃗ ⃗⃗ .𝒃 ⃗ ⃗⃗ = mn+pq = |𝒂 ⃗ ⃗⃗||𝒃 ⃗ ⃗⃗| Cos θ iff 𝒊 ⃗ .𝒊 ⃗ = 𝒋 ⃗ .𝒋 ⃗ = 𝟏 and 𝒊 ⃗ .𝒋 ⃗ = 𝒋 ⃗.𝒊 ⃗ = 0 (ii) Derivation of cross/vector product between two vectors in 2D Taking Sin to both sides of the expression θ2 – θ1 = θ, Sin θ = Sin (θ2 – θ1) = Sin θ2 Cos θ1 - Cosθ2Sinθ1………………….…….12
- 12. From 1, 2,3, 4 & 5, pn-mq = |𝒂 ⃗ ⃗⃗||𝒃 ⃗ ⃗⃗| Sinθ…………………………….……..13 Let 𝒊 ⃗ and 𝒋 ⃗ be two unit vectors along x-axis and y-axis respectively. Vectors can be represented in the form of unit vectors as: 𝒂 ⃗ ⃗⃗ = (m, p) = m𝒊 ⃗+p𝒋 ⃗ =𝒎 ⃗⃗⃗⃗+𝒑 ⃗ ⃗⃗………………………………………………………14 𝒃 ⃗ ⃗⃗ = (n, q) = n𝒊 ⃗+q𝒋 ⃗ ⃗⃗ = 𝒏 ⃗⃗⃗+𝒒 ⃗ ⃗⃗…………………………………………..……………15 From 7 & 8, m𝒊 ⃗ = 𝒎 ⃗⃗⃗⃗, n𝒊 ⃗ = 𝒏 ⃗⃗⃗, p𝒋 ⃗ = 𝒑 ⃗ ⃗⃗ and q𝒋 ⃗ ⃗⃗ =𝒒 ⃗ ⃗⃗ ……………………………..……………16 Multiplying 7 and 8, 𝒂 ⃗ ⃗⃗*𝒃 ⃗ ⃗⃗ = (m𝒊 ⃗+p𝒋 ⃗) * (n𝒊 ⃗+q𝒋 ⃗ ⃗⃗) 𝒂 ⃗ ⃗⃗*𝒃 ⃗ ⃗⃗= mn (𝒊 ⃗*𝒊 ⃗) + mq (𝒊 ⃗ *𝒋 ⃗ ) + pn (𝒋 ⃗ * 𝒊 ⃗) + pq (𝒋 ⃗*𝒋 ⃗)…………….……….17 For, 𝒊 ⃗ * 𝒊 ⃗ = 𝒋 ⃗ *𝒋 ⃗ = 𝟎, 𝒊 ⃗ *𝒋 ⃗ = −𝟏 & 𝒋 ⃗ *𝒊 ⃗ = 1 equation 10 becomes, 𝒂 ⃗ ⃗⃗*𝒃 ⃗ ⃗⃗= pn - mq………………………………………………………………… ……18 From 11 & 6, 𝒂 ⃗ ⃗⃗*𝒃 ⃗ ⃗⃗= pn - mq= |𝒂 ⃗ ⃗⃗||𝒃 ⃗ ⃗⃗| Sin θ 𝒏 ̂ iff 𝒊 ⃗ * 𝒊 ⃗ = 𝒋 ⃗ *𝒋 ⃗ = 𝟎, 𝒊 ⃗ *𝒋 ⃗ = −𝟏 & 𝒋 ⃗*𝒊 ⃗ = 1 Since, |𝒂 ⃗ ⃗⃗||𝒃 ⃗ ⃗⃗| Sin θ is a formula of area and area is a vector whose direction is normal to the plane, the expression is multiplied by the unit vector 𝒏 ̂.