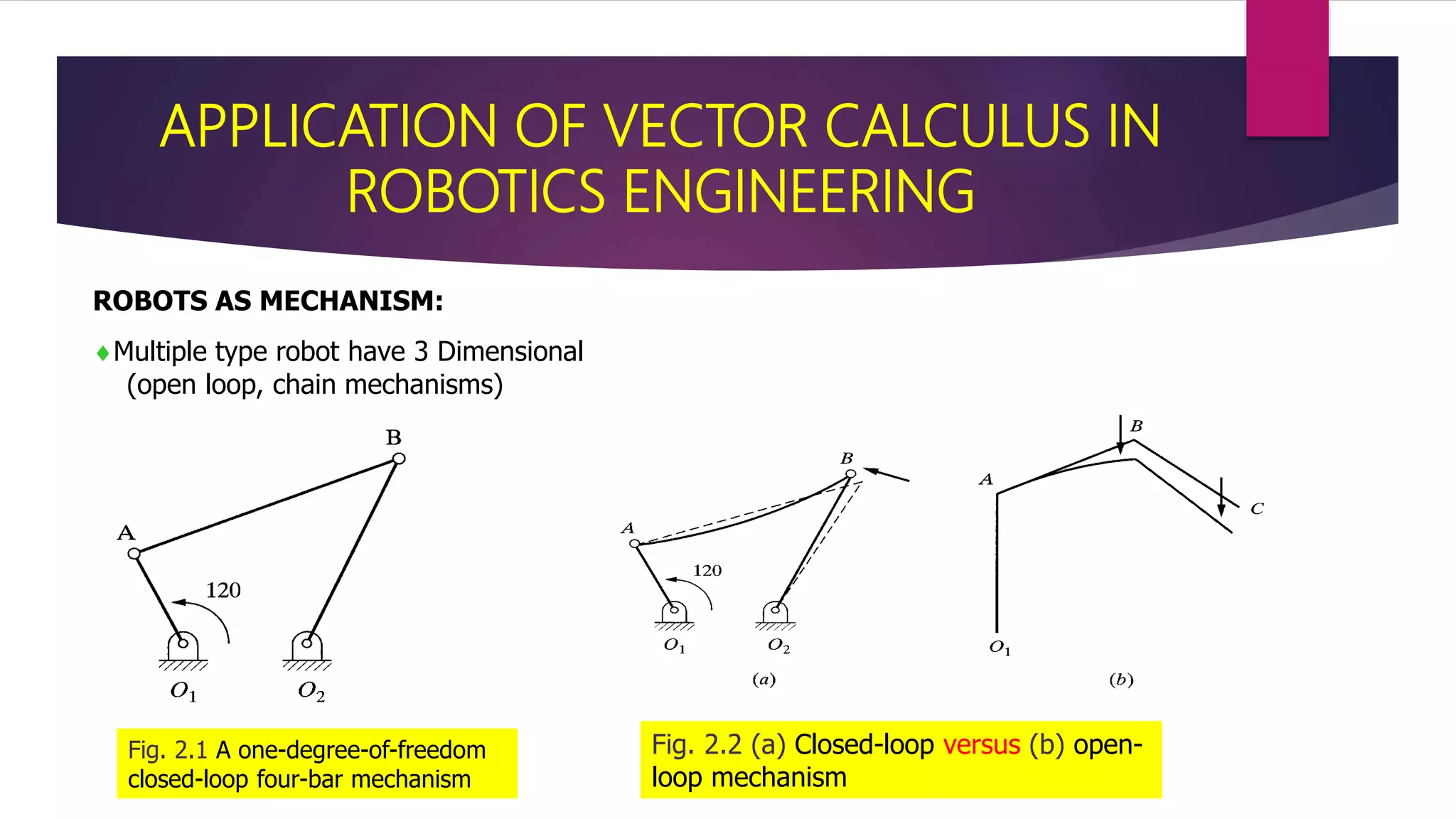
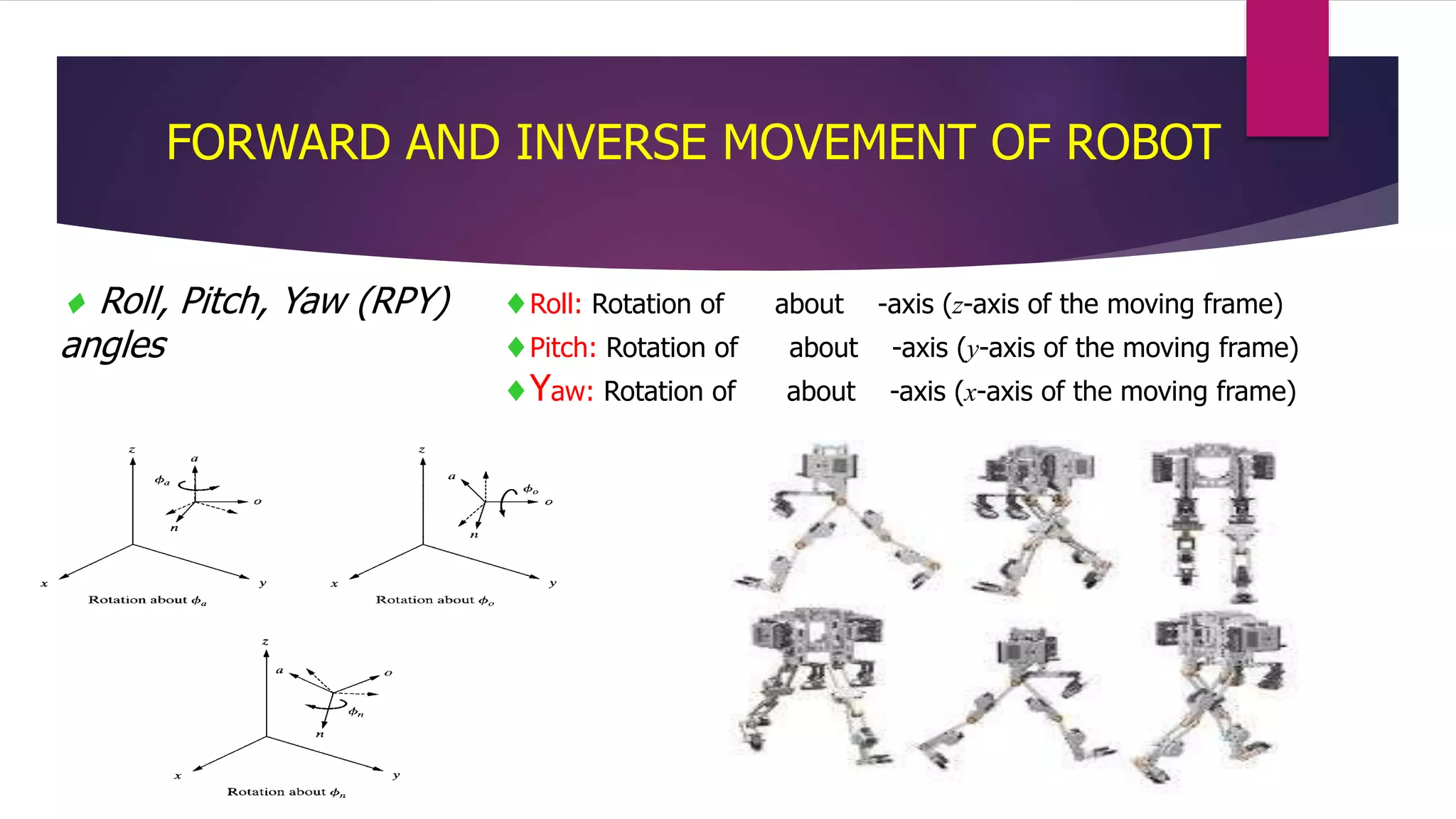
Vector calculus concepts such as angular velocity vectors, linear and rotational velocities, and Jacobians are important applications in robotics engineering. Vector calculus is used to represent points and vectors in robotic mechanisms with three coordinates and their magnitudes and directions. It allows determining the velocity of parts in a robot by propagating velocities between links using rotational and angular velocities. Jacobians relate Cartesian velocities to joint velocities in robots and are used for forward and inverse kinematics analysis to calculate robot positions and orientations.

1. APPLICATION OF VECTOR CALCULUS IN
ROBOTICS ENGINEERING
PRESENTED BY:-
NAVEEN A
SAISARAN K
ROOPESH P
PAAVAI ENGINEERING COLLEGE, (AUTONOMOUS) NAMAKKAL.

2. INTRODUCTION:
 Vector Calculus was developed by J. Willard
Gibbs.
 He was born on February 11 1839 United States.
 He studied at the Yale University.
 He is the founder of vector calculus.
 He died on April 28 1903.

3. VECTOR CALCULUS:
 Vector Calculus is a branch of mathematics concerned with differentiation
and integration of vector fields. Vector has both magnitude and direction.
The term “VECTOR CALCULUS” is sometimes used as a synonym for the
broader subject of multivariable calculus, which includes vector calculus as
well as partial differentiation and multiple integration.
 In vector calculus, various differential operators defined on scalar
or vector fields are studied, which are typically expressed in terms
of the del operator.
= (∂⁄∂x, ∂⁄∂y, ∂⁄∂z)

4. Do you know how the
VECTOR CALCULUS is
applied in ROBOTICS?

5. Movement Imitation - Example
vector calculus in robotics for the research path integration in robot
Navigation and path optimization technique using vector calculus.
Future technology in vector graphics is a humanoid robot.
VECTOR CALCULUS IN ROBOTICS

6. Position of tip in (x,y) coordinates

7. APPLICATION OF VECTOR CALCULUS IN
ROBOTICS ENGINEERING
ROBOTS AS MECHANISM:
Multiple type robot have 3 Dimensional
(open loop, chain mechanisms)
Fig. 2.1 A one-degree-of-freedom
closed-loop four-bar mechanism
Fig. 2.2 (a) Closed-loop versus (b) open-
loop mechanism

8. Representation of a Point in
ROBOT Mechanism:
A point P in Robot mechanism:
3 coordinates relative to a reference frame.
It has both magnitude and direction.
^^^
kcjbiaP zyx 
Representation of a point in space

9. Representation of a vector in space
A Vector P in robot mechanism:
3 coordinates of its tail and of its head
^^^__
kcjbiaP zyx 













w
z
y
x
P
__
Representation of a Vector in
ROBOT Mechanism:

10. Notations:
 The Angular Velocity Vector :
Angular velocity vector of a body ( is for a point) As a frame
represents the orientation of the body = rotational velocity of the frame.
Rotational velocity of frame {B} relative to frame {A}:
- it’s direction represents the instantaneous axis of rotation of {B}
relative to {A}
- it’s magnitude represents the speed of rotation.
the angular velocity of {B} relative to {A} expressed in {C}
In the universe frame {U}
10
  A
Cv
A
B 
 
C
A
B 
U
C C 

11. Linear and rotational velocities of rigid bodies
2. Rotational velocity: (Rotation only)
Two frames {A} and {B} have the same origin for all the time only the relative
orientation is changing in time 
is fixed in {B} 
What is the velocity of point Q in {A}
If is changing in {B}
11
A
B
B
Q 0B
QV 
 
A A A
Q B
A A B
B B
V Q
R Q
  
  
B
Q
?A
QV
   
 
A
A A A B B
Q B B Q
A A B A B
B B B Q
V R Q V
R Q R V
   
   

12. Velocity propagation from link to link
i
i
1
1
i
iv

i
iv
1
1
i
i

Starting from the base the velocity of any link
(i+1) equal to the previous link (i) + the relative
Velocity between (i+1) and (i)
• Angular velocity propagation
   
1 1
1
1 1 1 1 1 1
i i i
i i i
i i i i
i i i i i iz R z
 
 
 

     
  
   
1
1
0
0
1
i
iz

 
 
 
  
 
     
1
1 1 1 1
1 1 1 1
1 1 1 10 0 1
i i i i
i i i i i
Ti i i i i i
i i i i i i i i
R z
R z R
  
    

   
   
   
  
      

13. Jacobians
• In robotics, the Jacobian relates the Cartesian velocities with
joint velocities
≡ vector of joint angles
≡ vector of joint velocities
• General Case:
13
Instantaneous, as  is changing  J( ) is changing
11 12 1
21 22 20
1 2
( )
n
n
m m mn
J J J
J J J
J
J J J
 
 
  
 
 
 

14. Fig. 2.17 The hand frame of the robot relative to the reference frame.
Forward Kinematics Analysis:
• Calculating the position and orientation of the hand of the robot.
If all robot joint variables are known, one can calculate where the robot is
at any instant.
.
ROBOT NAVIGATION AND OPTIMIZATION
TECHNIQUE

15.  Roll, Pitch, Yaw (RPY)
angles
Roll: Rotation of about -axis (z-axis of the moving frame)
Pitch: Rotation of about -axis (y-axis of the moving frame)
Yaw: Rotation of about -axis (x-axis of the moving frame)
FORWARD AND INVERSE MOVEMENT OF ROBOT

16. CONCLUSION:
We have presented a novel neural framework for robot
navigation in a cluttered environment.
“A MATHEMATICIAN IS A BLIND MAN IN A
DARK ROOM LOOKING FOR A BLACK CAT
WHICH ISN’T THERE.”
-CHARLES DARWIN

17. Thank
you