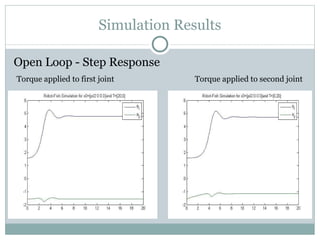
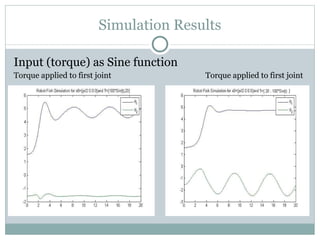
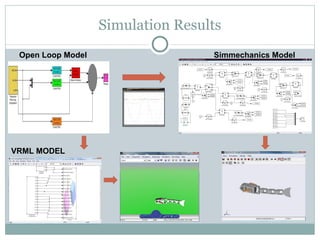
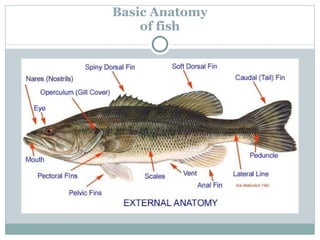
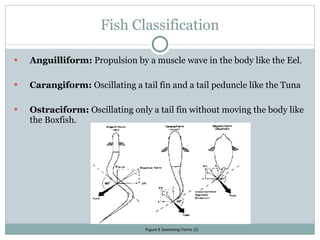
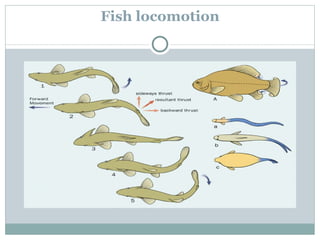
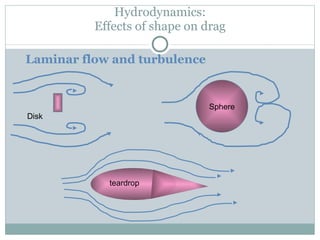
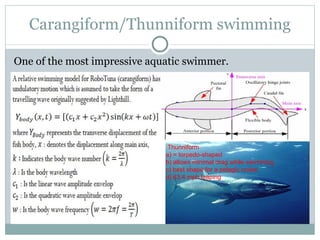
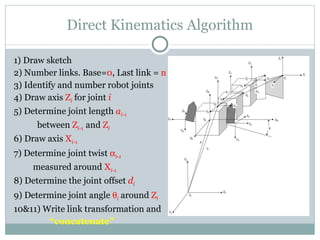
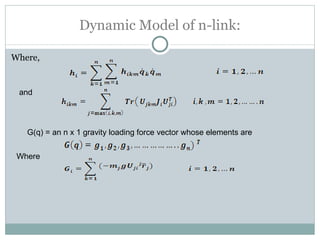
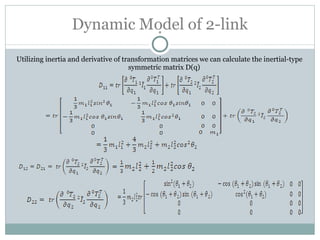
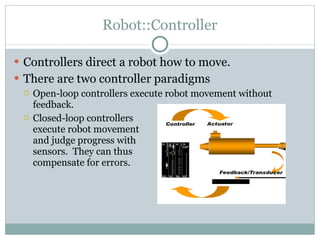
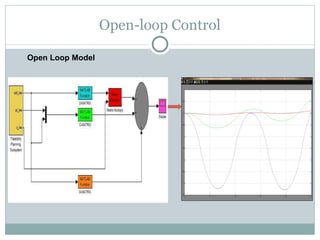
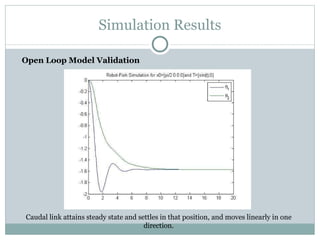
The document discusses the design of a robotic fish prototype. It covers the biomimetic inspiration of real fish motion, mathematical modeling including kinematics, dynamics, and degrees of freedom. Open and closed loop control strategies are examined through simulation. Potential applications of robotic fish include efficient ship propulsion and leading real fish to safety.

1. SUPERVISOR : A/P SANJIB KUMAR PANDA GUIDED BY : DR. RAJESH KUMAR Presented By: BHUNESHWAR PRASAD A0076967H ELECTRICAL ENGINEERING PROJECT PROJECT TITLE : ROBOT FISH

2. OUTLINE Introduction ( Biomimetic?, Previous Work, Project-Aims ) How do fish propel themselves in water? ( Fish Classification ,Motion types ) Mathematical Model ( Effecters & Actuators, DoF, Forward & Inverse Kinematics, Dynamics ) Controller ( Open loop Control, Closed loop Control ) Conclusion

3. Biomimetics

4. In this project… Building an electro-mechanical fish that mimics a real fish motion( prototype development under progress ) Kinematics and Dynamics analysis Overview Of Solidworks and 3 D Simulation Simulation Results ( open loop and closed loop control ) a a Z 0 X 0 Y 0 Z 3 X 2 Y 1 X 1 Y 2 d 2 Z 1 X 3 Z 2

5. Basic Anatomy of fish

6. Fish Classification Anguilliform: Propulsion by a muscle wave in the body like the Eel. Carangiform: Oscillating a tail fin and a tail peduncle like the Tuna Ostraciform: Oscillating only a tail fin without moving the body like the Boxfish. Figure 8 Swim ming Forms (2)

7. How do fish swim? Fi sh swim by their skeletons and muscles work together to allow them to swim . With pushing water away behind them, through by various methods. C.M. Breder (1966) classified into the following three general categories based on length of a tail fin and strength of its oscillation : (a) Anguilliform, (b) Carangiform, (c) Ostraciiform

8. Fish locomotion

9. Hydrodynamics: Effects of shape on drag Laminar flow and turbulence Disk Sphere teardrop

10. Carangiform/Thunniform swimming One of the most impressive aquatic swimmer. Thunniform a) = torpedo-shaped b) allows minimal drag while swimming c) best shape for a pelagic cruise d) 43.4 mph leaping

11. MATHEMATICAL MODELING Effectors and Actuators An effector is any device that affects the environment . A robot's effector is under the control of the robot. Effectors: Caudal fins, Pectoral fins, Dorsal fins, Pelvic and Anal fins. The role of the controller is to get the effectors to produce the desired effect on the environment , this is based on the robot's task.

12. Effectors and Actuators An actuator is the actual mechanism that enables the effector to execute an action. Actuators typically include : electric motors, hydrauli c cylinders, pneumatic cylinders, etc. The terms effector and actuator are often used interchangeably to mean "whatever makes the robot take an action." This is not really proper use : Actuators and effectors are not the same thing . And we'll try to be more precise .

13. Robot::Body Typically defined as a graph of links and joints : A link is a part, a shape with physical properties. A joint is a constraint on the spatial relations of two or more links .

14. Types of Joints Respectively, a ball joint , which allows rotation around x, y, and z, a hinge joint , which allows rotation around z, and a slider joint , which allows translation along x. These are just a few examples…

15. Degrees of freedom Most simple actuators control a single degree of freedom , i.e., a single motion (e.g., up-down, left-right, in-out, etc.). A motor shaft controls one rotational degree of freedom , for example. A sliding part on a crane controls one translational degree of freedom . How many degrees of freedom (DOF) a robot has is very important in determining how it can affect its world, and therefore how well, if at all, it can accomplish its task. We say many times that sensors must be matched to the robot's task. Similarly, effectors must be well matched to the robot's task also. When we design a robot our first task is decide the number of DOF and the geometry.

16. DOF In general, a free body in space has 6 DOF: three for translatio n (x,y,z), three for orientation/rotation (roll, pitch, and yaw). We need to know, for a given effector (and actuator/s): how many DOF are available to the robot , how many total DOF any given robot has. If there is an actuator for every DOF , then all of the DOF are controllable. Usually not all DOF are controllable , which makes robot control harder.

17. Definition of a HOLONOMIC robot When the number of controllable DOF is equal to the total number of DOF on a robot, the robot is called holonomic. If the number of controllable DOF is smaller than total DOF , the robot is non-holonomic. If the number of controllable DOF is larger than the total DOF , the robot is redundant. (like a human hand) Holonomic <= > Controllable DOF = total DOF Non-Holonomic <= > Controllable DOF < total DOF Redundant <= > Controllable DOF > total D OF

18. Kinematics Kinematics is the study of motion without regard for the forces that cause it. It refers to all time-based and geometrical properties of motion. It ignores concepts such as torque, force, mass, energy, and inertia . In order to control a ROBOT, we have to know its kinematics: 1. what is attached to what, 2. how many joints there are, 3. how many DOF for each joint, etc.

19. 1) Draw sketch 2) Number links. Base= 0 , Last link = n 3) Identify and number robot joints 4) Draw axis Z i for joint i 5) Determine joint length a i- 1 between Z i- 1 and Z i 6) Draw axis X i- 1 7) Determine joint twist  i - 1 measured around X i- 1 8) Determine the joint offset d i 9) Determine joint angle  i around Z i 10&11) Write link transformation and “ concatenate” Direct Kinematics Algorithm

20. Denavit-Hartenberg Convention Given the starting configuration of the mechanism and joint angles, we can compute the new configuration. For a mechanism robot, this would mean calculating the position and orientation of the end effector given all the joint variables. Denavit-Hartenberg Convention Link and Joint Parameters Joint angle θ i : the angle of rotation from the X i-1 axis to the X i axis about the Z i-1 axis. It is the joint variable if joint i is rotary. Joint distance di : the distance from the origin of the (i-1) coordinate system to the intersection of the Z i-1 axis and the X i axis along the Z i-1 axis. It is the joint variable if joint i is prismatic. Link length ai : the distance from the intersection of the Z i-1 axis and the X i axis to the origin of the ith coordinate system along the X i axis. Link twist angle α i : the angle of rotation from the Z i-1 axis to the Z i axis about the X i axis.

21. Denavit-Hartenberg Parameters Identified link parameters for the Robotic Fish model . Transformation Matrix: = Where and were the corresponding rotational and translational matrices respectively.

22. Dynamic Model of n-link: Dynamic model robot can be calculated by the below mentioned equation: D(q) = a n x n inertial acceleration - related symmetric matrix whose elements are: ) = an n x 1 nonlinear Coriolis and centrifugal force vector whose elements are =

23. Dynamic Model of n-link: Where, and G(q) = an n x 1 gravity loading force vector whose elements are Where

24. Dynamic Model of 2-link Based on the Lagrange –Euler methodology, Dynamics model for two links is shown below. For calculating the Dynamics of the whole model is done through MATLAB. Employing velocity coefficients matrix for revolute joints, we can write: The standard matrix for revolute joint is represented as

25. Dynamic Model of 2-link Assuming all the product of inertias is zero, we find:

26. Dynamic Model of 2-link Utilizing inertia and derivative of transformation matrices we can calculate the inertial-type symmetric matrix D(q) =

27. Dynamic Model of 2-link We can calculate the value for ,

28. Dynamic Model of 2-link Next we need to derive the gravity related terms,

29. Dynamic Model of 2-link Finally Lagrange-Euler equation of motion for two link manipulator are found and shown below:

30. Robot::Controller Controllers direct a robot how to move. There are two controller paradigms Open-loop controllers execute robot movement without feedback. Closed-loop controllers execute robot movement and judge progress with sensors. They can thus compensate for errors.

31. Open-loop Control Open Loop Model

32. Simulation Results Open Loop Model Validation Caudal link attains steady state and settles in that position, and moves linearly in one direction.

33. Simulation Results x 0 = [-pi/2 -pi/2 ] x 0 = [pi/2 -pi/2 ]

34. Simulation Results x 0 = [pi/2 pi/2] x 0 = [-pi/2 pi/2 ]

35. Simulation Results Open Loop - Step Response Torque applied to first joint Torque applied to second joint

36. Simulation Results Input (torque) as Sine function Torque applied to first joint Torque applied to first joint

37. Simulation Results Open Loop Model Simmechanics Model VRML MODEL

38. How can robot fish be used? There are many recent researches about biomimetic fish robot area such as Robo Tuna, ESSEX ROBOTIC FISH, STINGRAY. These studies can suggest a new and high efficient propulsion device for the ship or underwater vehicle.

39. For example, Maurizio Porfiri, assistant professor at Polytechnic Institute of New York University, has designed a robotic fish that leads real fish to safe water. Currently, the robotic fish can lead fish away from power plant turbines. Figure 2 3: Robotic Fish that protects fish from danger

40. Conclusion L earn t the different motion types and the needed mechanisms for the prototype development. T o implement these mechanisms, controller development is required. T ried to inspire by biological fishes ’ motion

41. References How a Fish Can Swim? Retrieved in December 16, from How Does a Fish Swim? | eHow.com http://www.ehow.com/how-does_4690184_a-fish-swim.html#ixzz18NF80duo Principles of the Swimming Fish Robot , Retrieved in December 17, from http://www.nmri.go.jp/eng/khirata/fish/general/principle/index_e.html Propulsion Technology, Retrieved in December 17, from http://www.tailboats.com/propulsion_technology.html Robo Tuna II , Retrieved In 17 December, from http://web.mit.edu/towtank/www/Tuna/Tuna2/tuna2.html Robotic fish that protect fish from danger, Retrieved in 19 December, from http://www.goodcleantech.com/2010/06/nyu_scientist_develops_robotic.php Why do Fish Have Scales? Retrieved in December 14, from http://www.letusfindout.com/why- do-fish-have-scales/ Why do Fish go belly up when they die? , Retrieved in December 18, from http://www.answerbag.com/q_view/153382#ixzz18NZ1QtVw