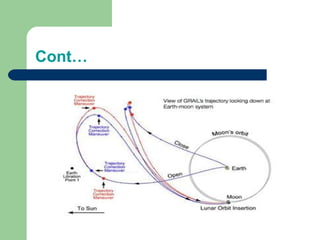
The document discusses complex integration, defining it as the integral of a function along an open or closed curve in the complex plane. It outlines various applications in physics, medical science, chemistry, signal analysis, computer science, electrical engineering, fluid dynamics, and civil and mechanical engineering. Additionally, it highlights the importance of complex numbers in describing and solving real-world problems in these fields.

2. Presented by:
SOHAIL AKBAR
UNIVERSITY of Engineering and
Technology , Taxila
COMSATS university . wah
Complex Integration its uses and types

3. Outline of Presentation
 Definition
 Real Life Applications
 Types
 Bibliography

4.  The integration of a function of a complex variable
along an open or closed curve in the plan of the
complex variable is called complex integration.
Close and Open Curve
Definition

5. 2nd
Definition
If f(z) is a single-valued, continuous function in some region R in the complex
plane then we define the integral of f(z) along a path C in R as in Fig.
( ) ( )( ).
C C
f z dz u iv dx idy= + +∫ ∫

6. Application in Physics
 To calculate the center of mass, center of gravity and
mass moment of inertia of vehicles, satellites.
 To calculate the velocity and trajectory of a satellite while
placing it an orbit like exactly which point you need to
give how much thrust to get the desired trajectory.
Applications

7. Cont…

8. Cont…
Application in Medical Science
 To study the spread of infectious disease.
 To determine how far and fast a disease is spreading,
where it may have originated from and how to best
treat it.

9. Cont…

10. Application in Chemistry
 To determine the rate of a chemical reaction and to
determine some necessary information of Radioactive
decay reaction.
Cont…

11. Cont…
Signal Analysis
 Complex numbers are used in signal analysis and other
fields for a convenient description for periodically
varying signals.
Arithmetic and Logic in Computer Science
 Algorithms for performing operations like addition,
subtraction, multiplication, and division in digital
computer systems are presented, with the goal of
explaining the concepts behind the algorithms.

12. Cont…
Electrical Engineering
 It helps us understand the behaviour of circuits which
contain reactance (produced by capacitors or inductors)
when we apply a.c. signals.
 It gives us a new way to think about oscillations. This is
useful when we want to apply concepts like the
conservation of energy to understanding the behaviour
of systems which range from simple a mechanical
pendulums to a quartz-crystal oscillator.

13. Cont…
Fluid Dynamics
 Influid dynamics, complex functions are used to
describe potential flow in two dimensions.
 Used in calculating forces and moments on aircraft, the
mass flow of petroleum through pipelines, and
prediction of weather patterns.

14. Civil and Mechanical Engineering
 The concept of complex geometry and Argand plane is
very much useful in constructing buildings and cars.
 This concept is used in 2-D designing of buildings and
cars.
 It is also very useful in cutting of tools.
 Another possibility to use complex numbers in simple
mechanics might be to use them to represent rotations.
Cont…

15. Types
1. Integrals of trigonometric functions from 0 to
2π:
2. Integral from
3. Combine 1 and 2
2
0
( )I trig function d
π
θ= ∫
to−∞ + ∞
( )I f x dx
+∞
−∞
=∫
trig function
I dx
polynomial
+∞
−∞
= ∫

16. Bibliography
[1] http://www.math.toronto.edu/mathnet/questionCorner/complexinlife.html
[2] http://www.physicsforums.com/showthread.php?t=159099
[3] http://www.ebookpdf.net/_engineering-application-of-complex-number-
(pdf)_ebook_.html.
[4] http:www.wikipedia.org.
[5] http://mathworld.wolfram.com
[6] http://euclideanspace.com