The guest lecture, given by Dr. Alaa Khamis at the University of Waterloo for ECE 486, focuses on the fundamentals of motion planning in robotics, covering concepts such as path planning, planning algorithms, and trajectory planning for robot manipulators. Key topics include discrete and combinatorial planning methods, configuration space representation, and the requirements of effective path planners. The lecture emphasizes the practical application of these concepts across multiple robotic systems and discusses the challenges of determining collision-free paths in dynamic environments.




![5Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Q: How can I get there from here?
A: Planning
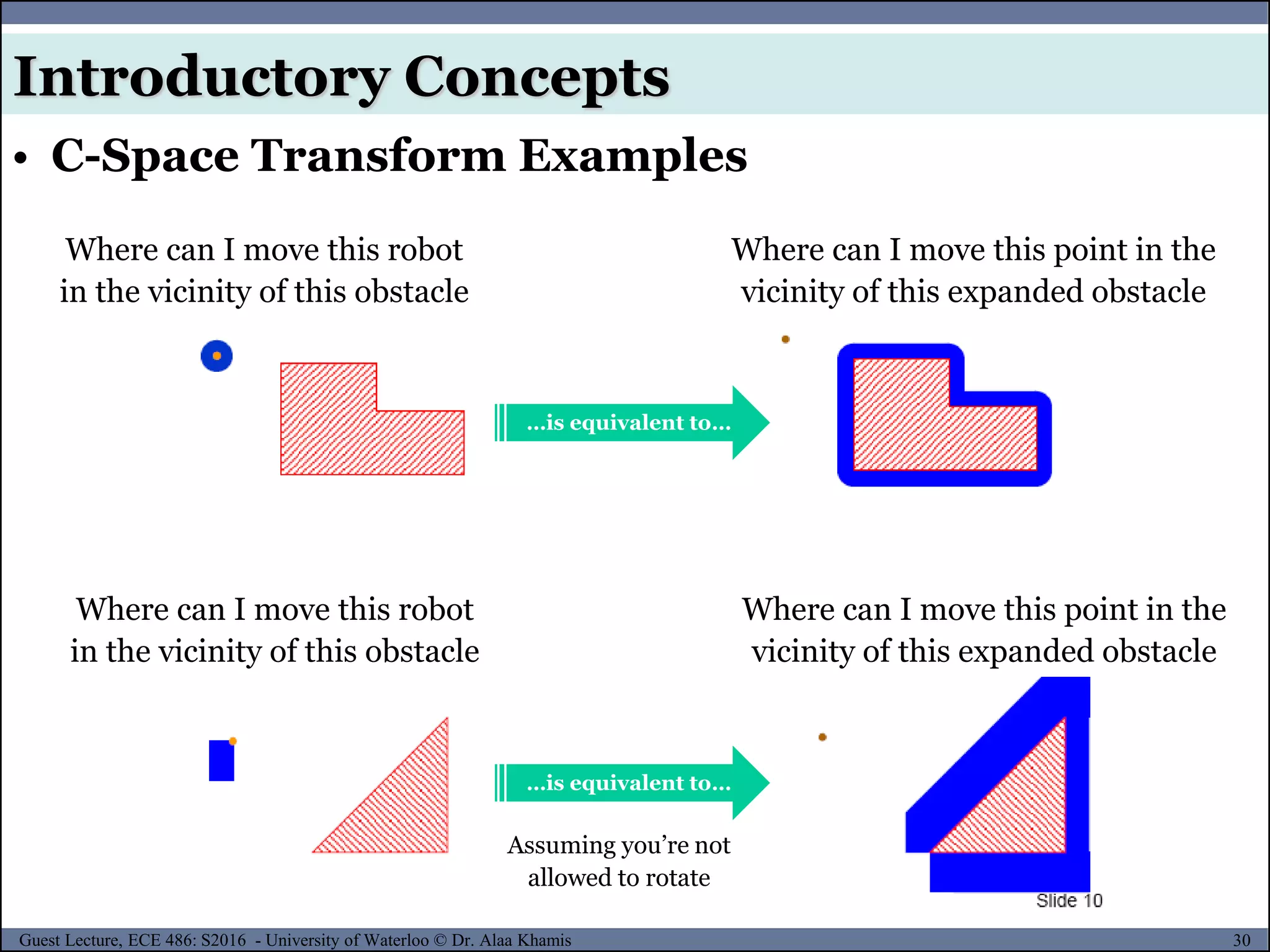
Introductory Concepts
Topic
High-level Functions
Partially understood
Not fully localized
Low-level Functions
Fully understood
Localized
Perception
Situation awareness
Natural Language Understanding
Pattern Discovery
Reasoning
Decision Making
Planning
Learning
etc.
SmellHearing Taste TouchSight
Brain functions
[1]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-5-2048.jpg)

![7Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Planning is everywhere
Introductory Concepts
AI Discrete Planning [2]
Piano Mover Problem [2] Unmanned Vehicles (UXVs) Planning
Rubik’s cube Sliding Puzzle
Robot Manipulator Planning
Unmanned
Aerial Vehicles
(UAV) & Micro
Aerial Vehicles
(MAV)
Unmanned
Underwater
Vehicles
(UUV)
Unmanned
Surface
Vehicles
(USV)
Unmanned
Ground
Vehicles
(UGV)](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-7-2048.jpg)



![11Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Introductory Concepts
• Planning Overview: Planning Environment
Kinds of events that trigger planning [3]:
Time-based: for example, a plan for automated
guided vehicle (AGV) needs to be made each season.
Event-based: a plan for AGV must be made after an event,
for example, a rush order in a factory.
Disturbance-based: a
plan must be adjusted
because a disturbance
occurs that renders the
plan invalid- for example,
unexpected moving
obstacle in the robot way. For reading: Can You Program Ethics Into a Self-Driving Car?](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-11-2048.jpg)


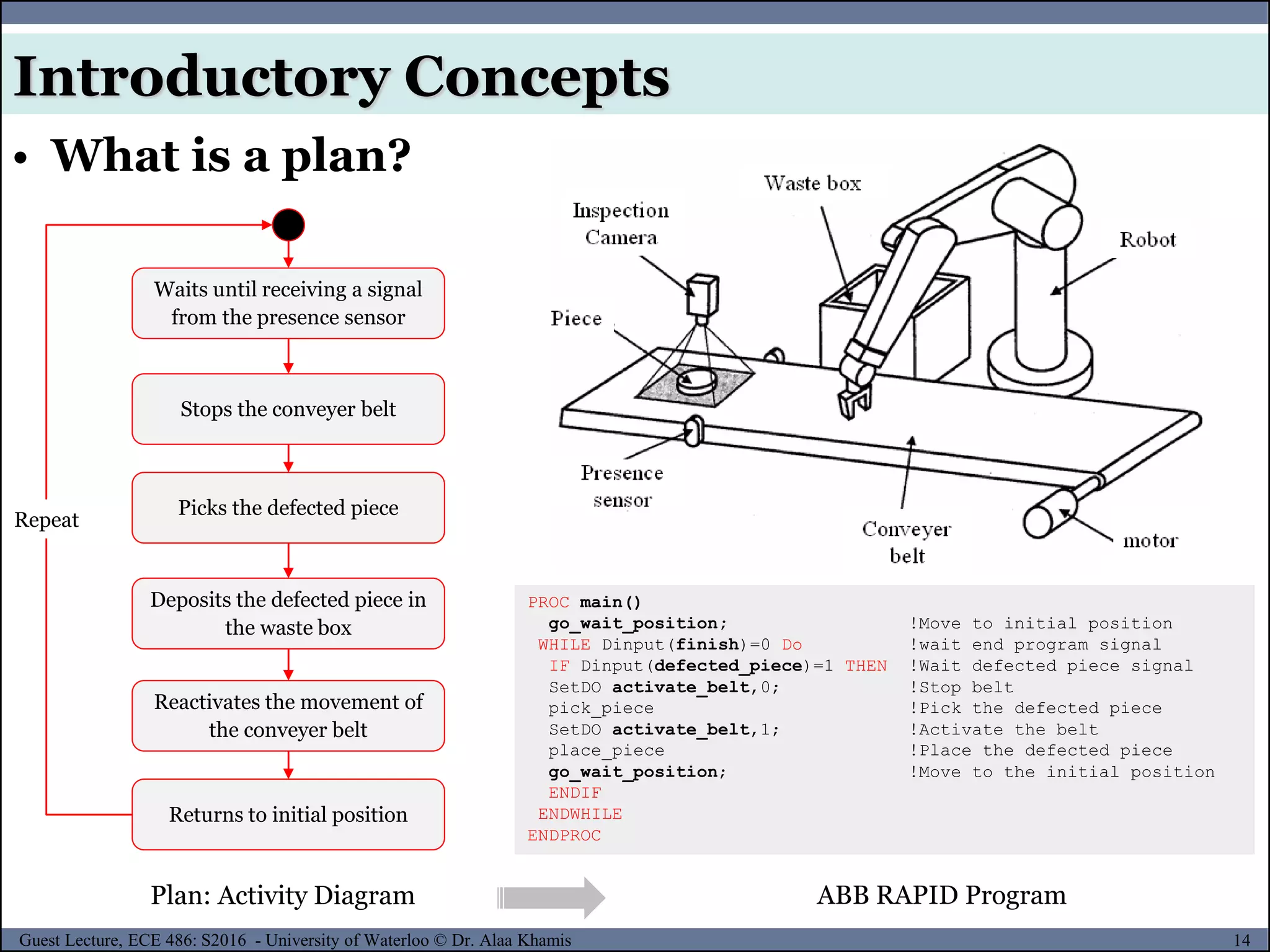




![19Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• What are the requirements of a path planner?
5. Determine the following:
Introductory Concepts
◊ Horizon: What time/space span does the
plan cover? Receding Horizon Control/planning (RHC)
◊ Frequency: How often is the plan created
or adapted?
[3]
◊ Level of detail: Does the plan need more detail in order to
be executed? Does the executing entity have to fill in the
details, or the plan used as a template for another planner
(multiresolutional planning)?
◊ (Re)presentation: How is the plan represented and
depicted? Does it specify the end state, or does it provide a
process description that leads to the end state?](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-19-2048.jpg)
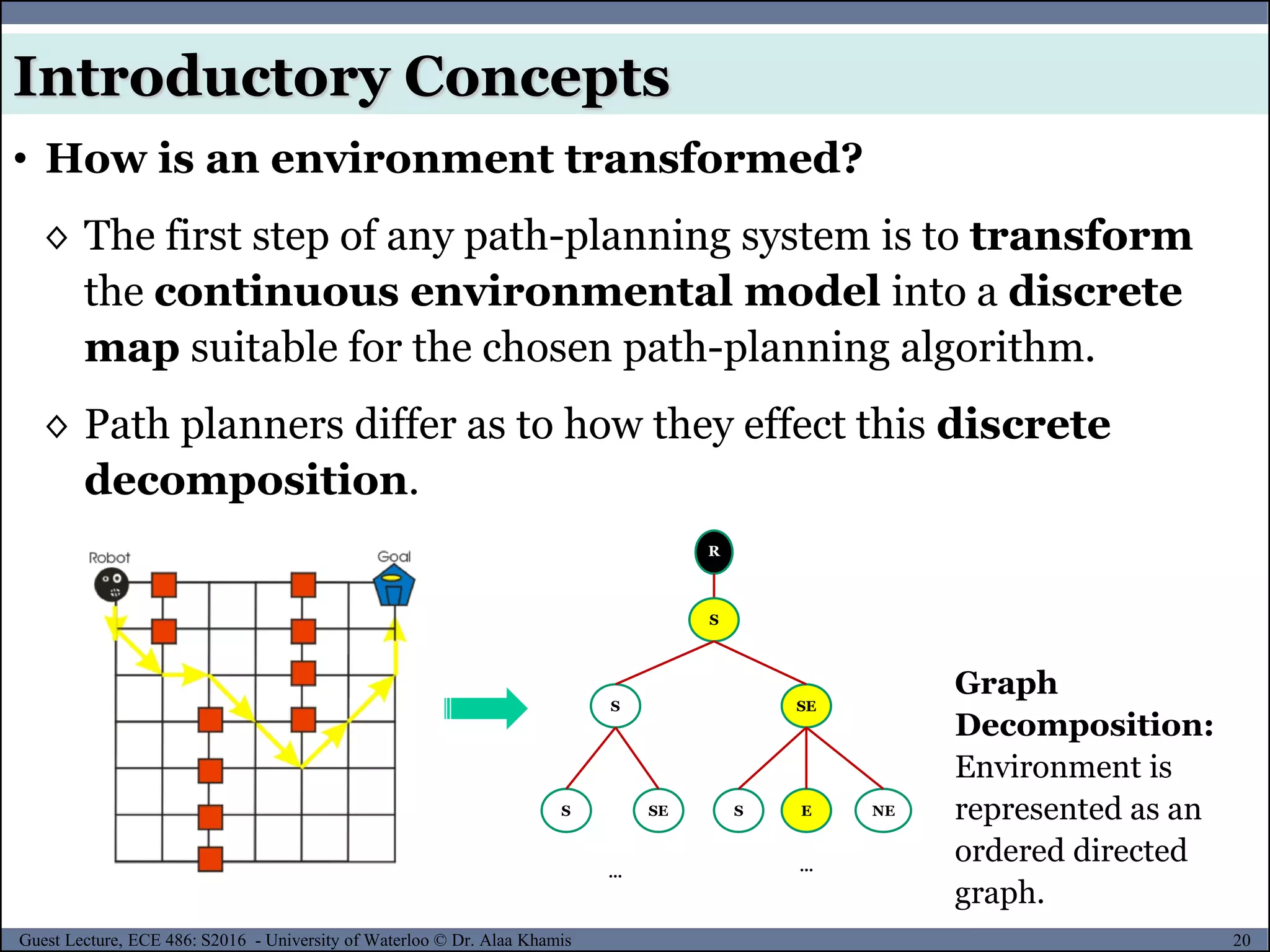

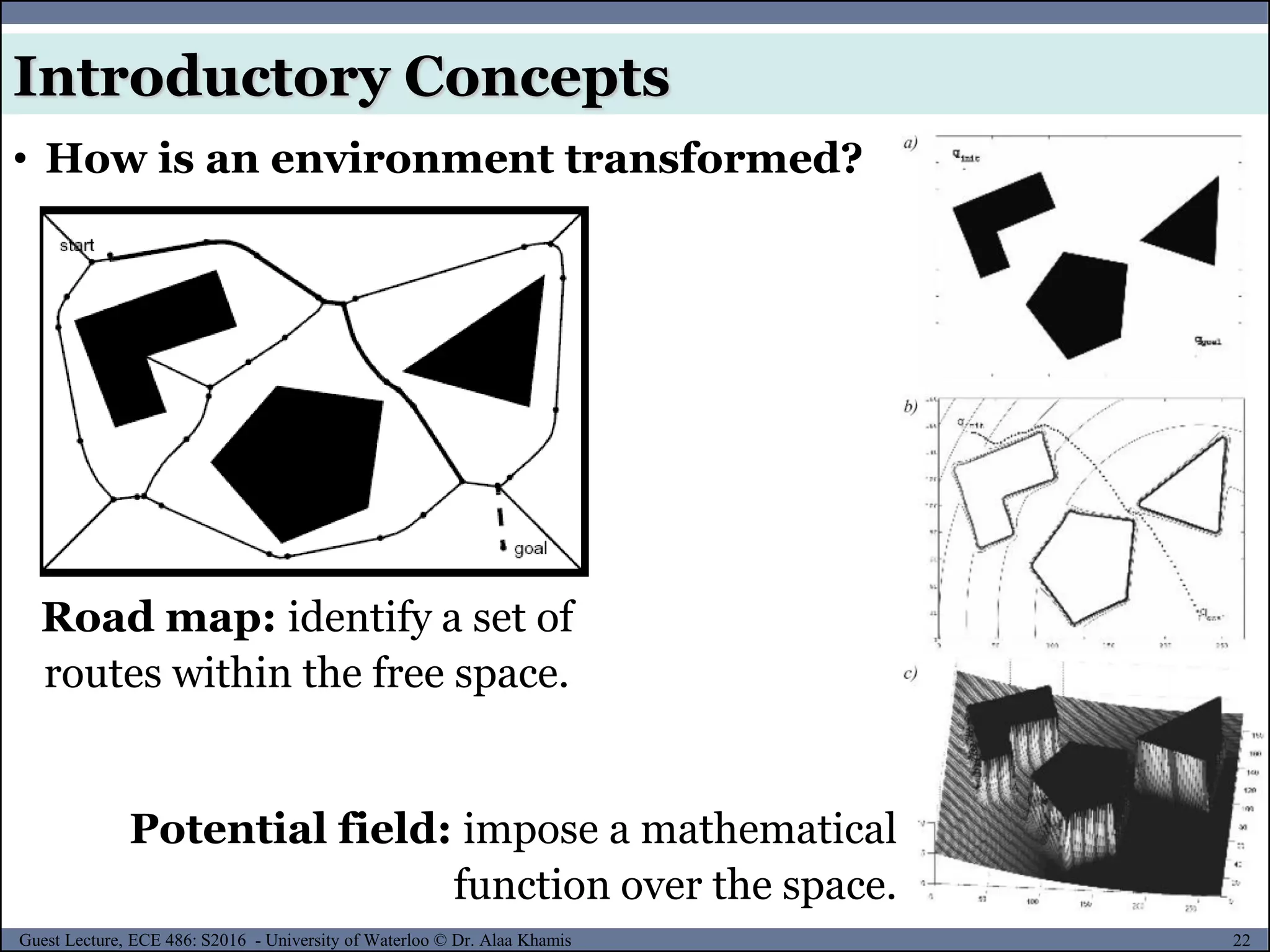

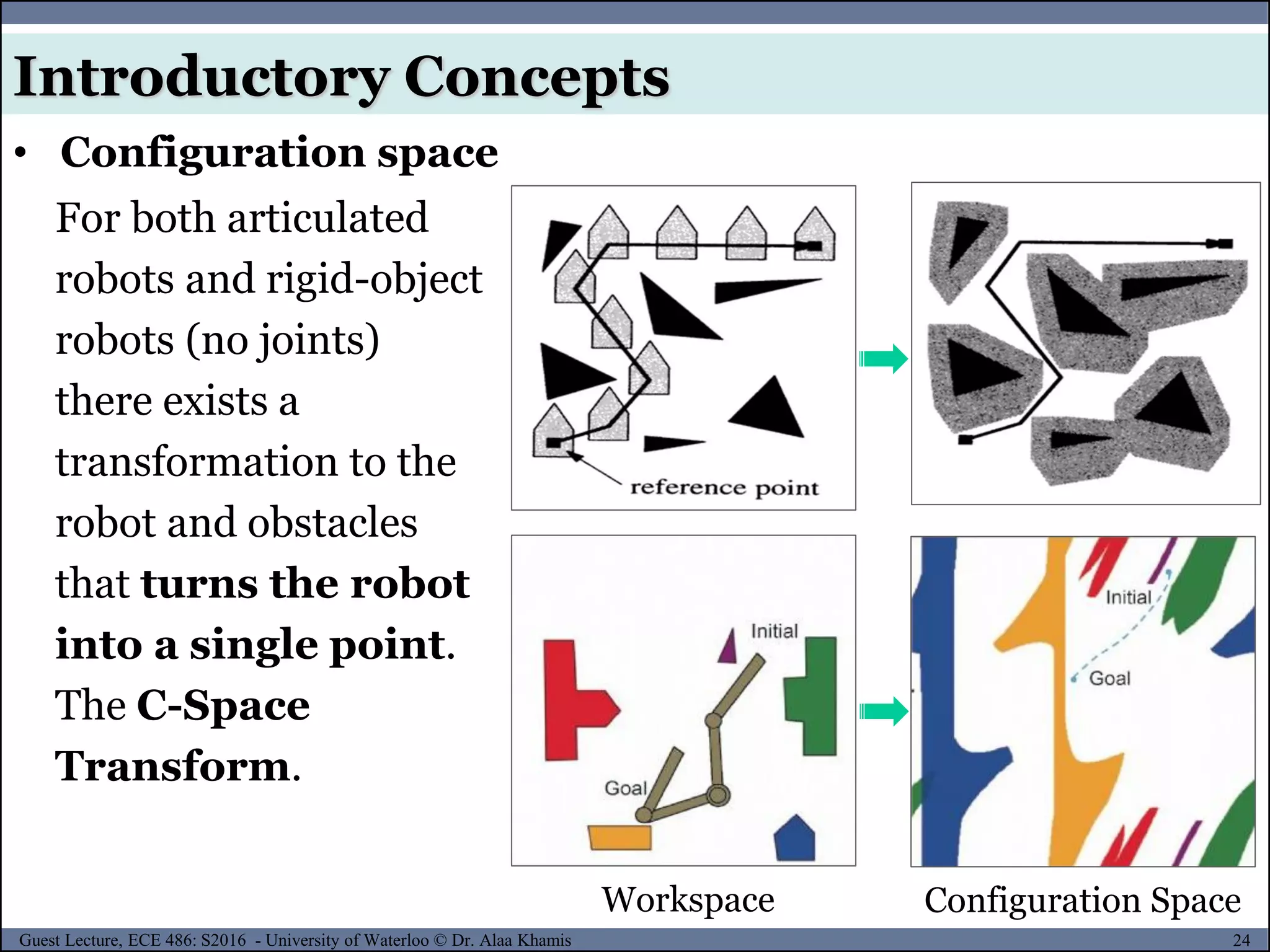
![25Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Introductory Concepts
• Configuration space
Assume the following:
[4]
𝒜 : a rigid/articulated robot;
𝒲 : the workspace (i.e., the Cartesian
space in which the robot moves);
𝒜(𝑞) : the subset of the workspace that is
occupied by the robot at configuration q
𝒪𝑖 : the obstacles in the workspace;
𝒪 = ⋃𝒪𝑖, obstructive region and
𝒞 : configuration space, which is the set of all possible
configurations. A complete specification of the location of every
point on the robot is referred to as a configuration.](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-25-2048.jpg)
![26Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Introductory Concepts
• Configuration space
[4]
𝒞obs: configuration space obstacle,
which is the set of configurations for
which the robot collides with an
obstacle, 𝒞obs ⊆ 𝒞
The set of collision-free configurations, referred to as the free
configuration space, is then simply
𝒞free = 𝒞𝒞obs
𝒞obs = 𝑞 ∈ 𝒞|𝒜(𝑞)⋂𝒪 ≠ 𝜙
𝒞 = 𝒞free ∪ 𝒞obs](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-26-2048.jpg)
![27Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Introductory Concepts
• Configuration space
[4]
The path planning problem is to find a
path from an initial configuration qinit to a
final configuration qfinal, such that the robot
does not collide with any obstacle as it
traverses the path.
A collision-free path from qinit to qfinal is a continuous map,
𝒯: 0,1 → 𝒞free
with
𝒯(0)= qinit and
𝒯(1)= qfinal
qinit
qfinal
𝒞free
𝒞obs](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-27-2048.jpg)
![28Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Introductory Concepts
• Configuration space: Articulated Robots
Consider a two-link planar arm in a workspace containing a
single obstacle
Two-link Planar Arm Configuration Space
[4]
The region 𝒞obswas computed
using a discrete grid on the
configuration space
Collision-free cells
Obstructive
cells](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-28-2048.jpg)







![37Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Who or what is going to use the plan?
global
local
Raw data
Environment Model
Local Map
“Position”
Global Map
Actuator Commands
Sensing Acting
Information
Extraction
Path
Execution
Cognition
Path Planning
Knowledge,
Data Base
Mission
Commands
Path
Real World
Environment
Localization
Map Building
MotionControl
Perception
[5]
Introductory Concepts](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-37-2048.jpg)




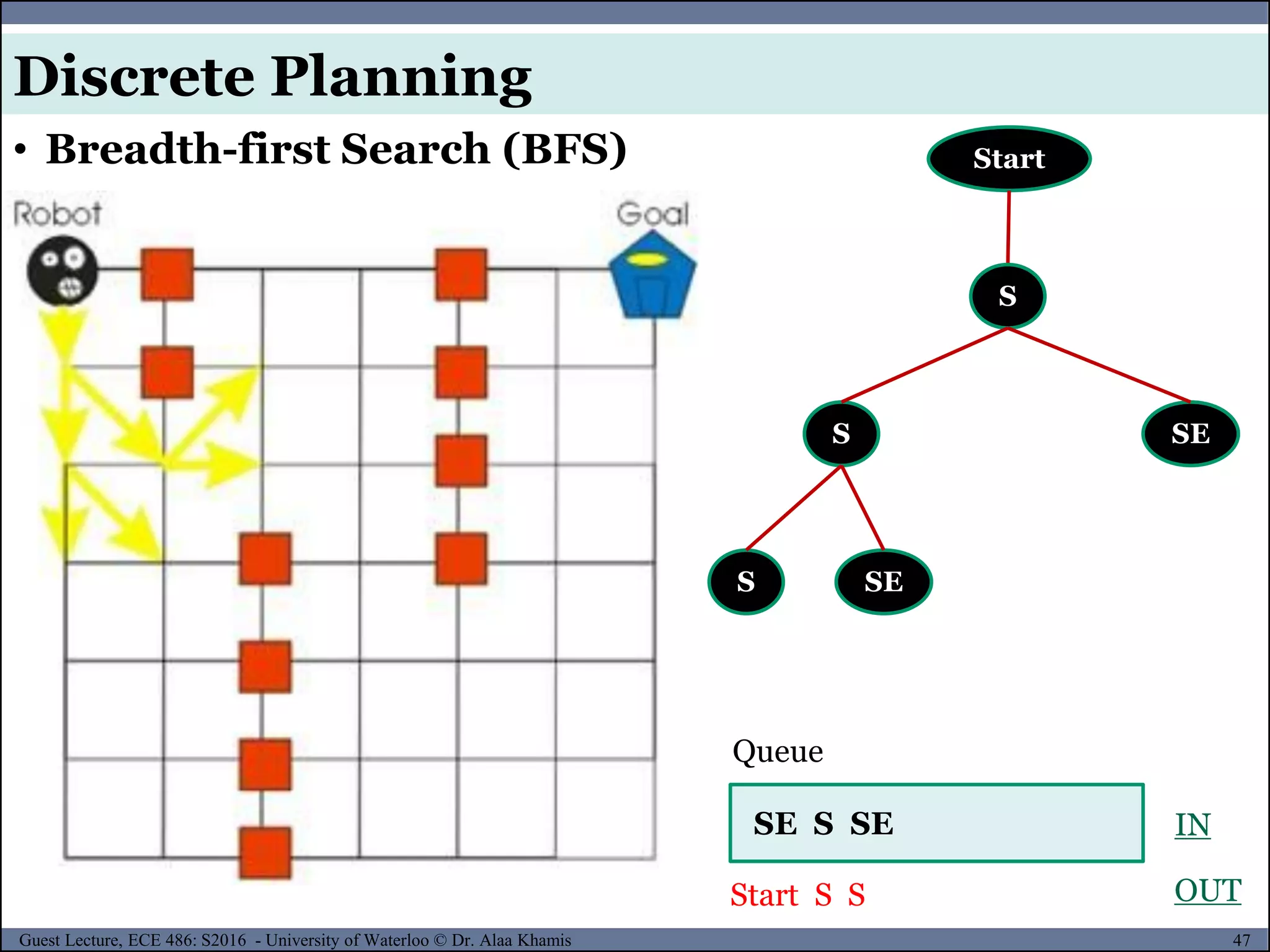
![42Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Step 1. Form a queue Q and set it to the initial state (for example, the Root).
Step 2. Until the Q is empty or the goal state is found
do:
Step 2.1 Determine if the first element in the Q is the goal.
Step 2.2 If it is not
Step 2.2.1 remove the first element in Q.
Step 2.2.2 Apply the rule to generate new state(s) (successor states).
Step 2.2.3 If the new state is the goal state quit and return this state
Step 2.2.4 Otherwise add the new state to the end of the queue.
Step 3. If the goal is reached, success; else failure.
[6]
• Breadth-first Search (BFS)
Discrete Planning](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-42-2048.jpg)

![44Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Start
Queue
Start IN
OUT
• Breadth-first Search (BFS)
Discrete Planning
[7]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-44-2048.jpg)













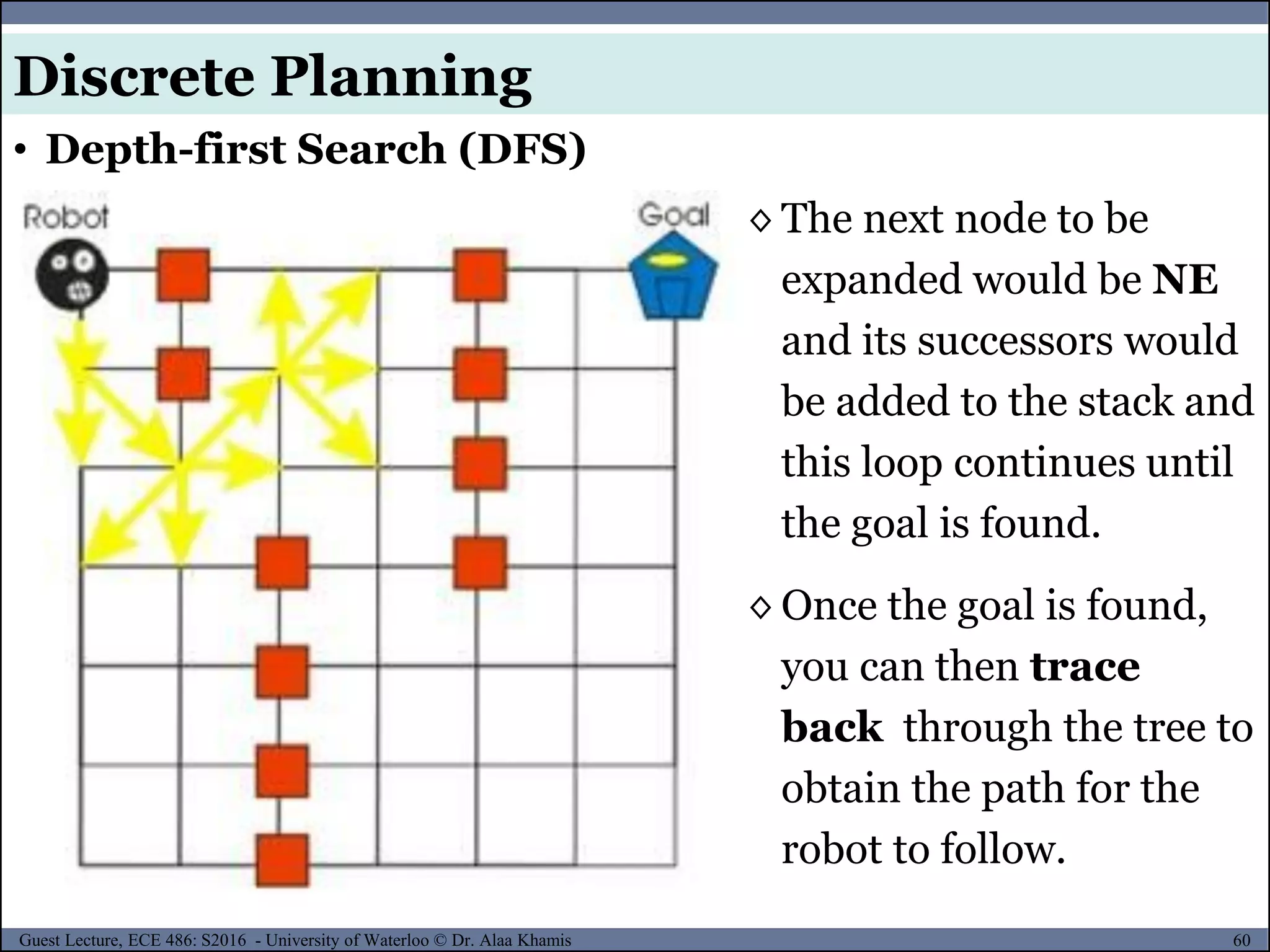




![65Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
◊ Blind search finds only one arbitrary solution instead of
the optimal solution.
◊ To find the optimal solution with DFS or BFS, you must not
stop searching when the first solution is discovered. Instead,
the search needs to continue until it reaches all the solutions,
so you can compare them to pick the best.
◊ The strategy for finding the optimal solution is called British
Museum search or brute-force search.
The inventors called this procedure the British Museum
algorithm "... since it seemed to them as sensible as
placing monkeys in front of typewriters in order to
reproduce all the books in the British Museum [5]."
• British Museum Search
Discrete Planning](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-65-2048.jpg)

![67Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
1. Init
Set start distance to 0, dist[s]=0,
others to infinite: dist[i]= (for is),
Set Ready = { } .
2. Loop until all nodes are in Ready
Select node n with shortest known distance that is not in Ready
set Ready = Ready + {n} .
FOR each neighbor node m of n
IF dist[n]+edge(n,m) < dist[m] /* shorter path found */
THEN { dist[m] = dist[n]+edge(n,m); pre[m] = n;}
• Dijkstra’s Algorithm
Discrete Planning](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-67-2048.jpg)
![68Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
S
c
0
a
d
b
10
9
9
3
2
5
6
1
From s to: S a b c d
Distance 0
Predecessor - - - - -
Step 0: Init list, no predecessors
Ready = {}
[7]
• Dijkstra’s Algorithm
Discrete Planning](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-68-2048.jpg)




![74Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Shortest path between s and a is {S, c, a} length=8
S
c
0
a
d
b
8
5 7
9
10
9
9
3
2
5
6
1
From s to: S a b c d
Distance 0 8 9 5 7
Predecessor - c a s c
◊ dist[a] = 8
◊ pre[a] = c
◊ pre[c] = S
◊ Shortest path:
Sc a,
◊ Length is 8
• Dijkstra’s Algorithm
Discrete Planning](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-74-2048.jpg)
![75Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Shortest path between s and b is {S, c, a,b} length=9
S
c
0
a
d
b
8
5 7
9
10
9
9
3
2
5
6
1 ◊ dist[b] = 9
◊ pre[b] = a
◊ pre[a] = c
◊ pre[c] = S
◊ Shortest path:
Sc a b
From s to: S a b c d
Distance 0 8 9 5 7
Predecessor - c a s c
• Dijkstra’s Algorithm
Discrete Planning](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-75-2048.jpg)
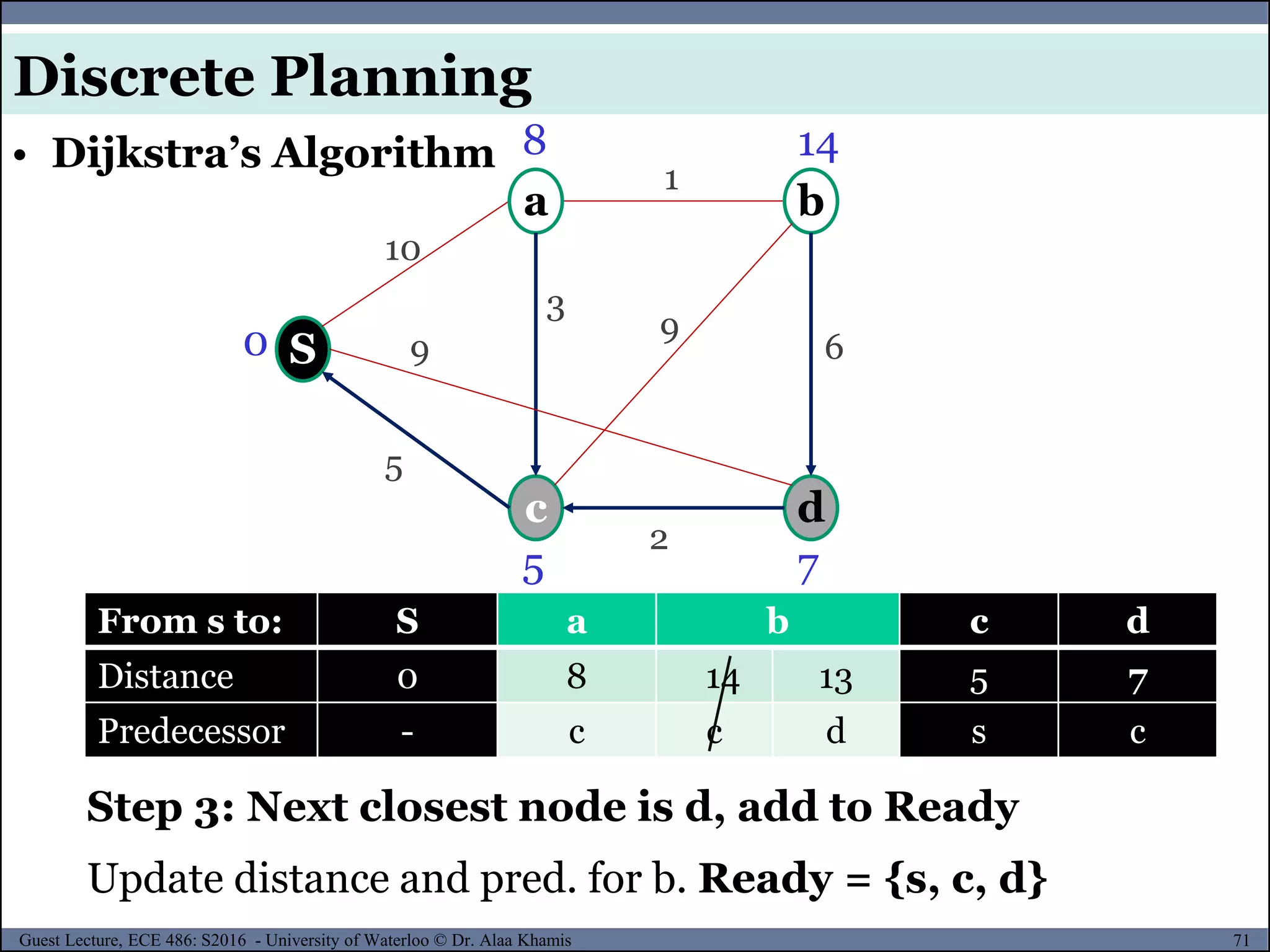
![76Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Shortest path between s and d is {S, c} length=5
S
c
0
a
d
b
8
5 7
9
10
9
9
3
2
5
6
1 ◊ dist[c] = 5
◊ pre[c] = S
◊ Shortest path:
Sc
From s to: S a b c d
Distance 0 8 9 5 7
Predecessor - c a s c
• Dijkstra’s Algorithm
Discrete Planning](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-76-2048.jpg)
![77Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Shortest path between s and d is {S, c, d} length=7
S
c
0
a
d
b
8
5 7
9
10
9
9
3
2
5
6
1 ◊ dist[d] = 7
◊ pre[d] = c
◊ pre[c] = S
◊ Shortest path:
Sc d
From s to: S a b c d
Distance 0 8 9 5 7
Predecessor - c a s c
• Dijkstra’s Algorithm
Discrete Planning](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-77-2048.jpg)
![78Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Dijkstra’s Algorithm
Discrete Planning
As can be seen from previous example, instead of solving
subproblems recursively, solve them sequentially and store their
solutions in a table. The trick is to solve them in the right order
so that whenever the solution to a subproblem is needed, it is
already available in the table [I. Parberry. Problems on algorithms. Prentice-Hall, 1995].](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-78-2048.jpg)











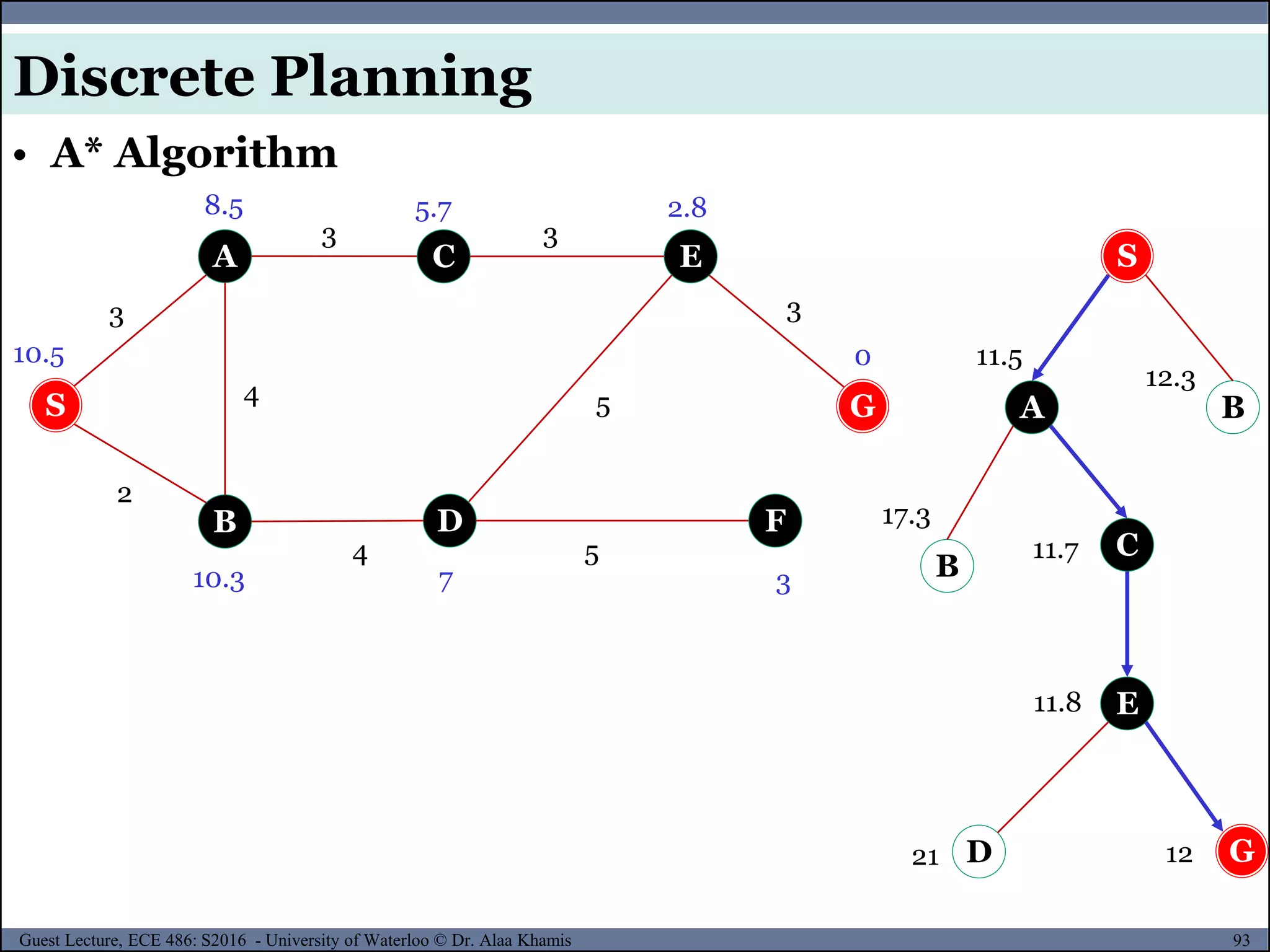



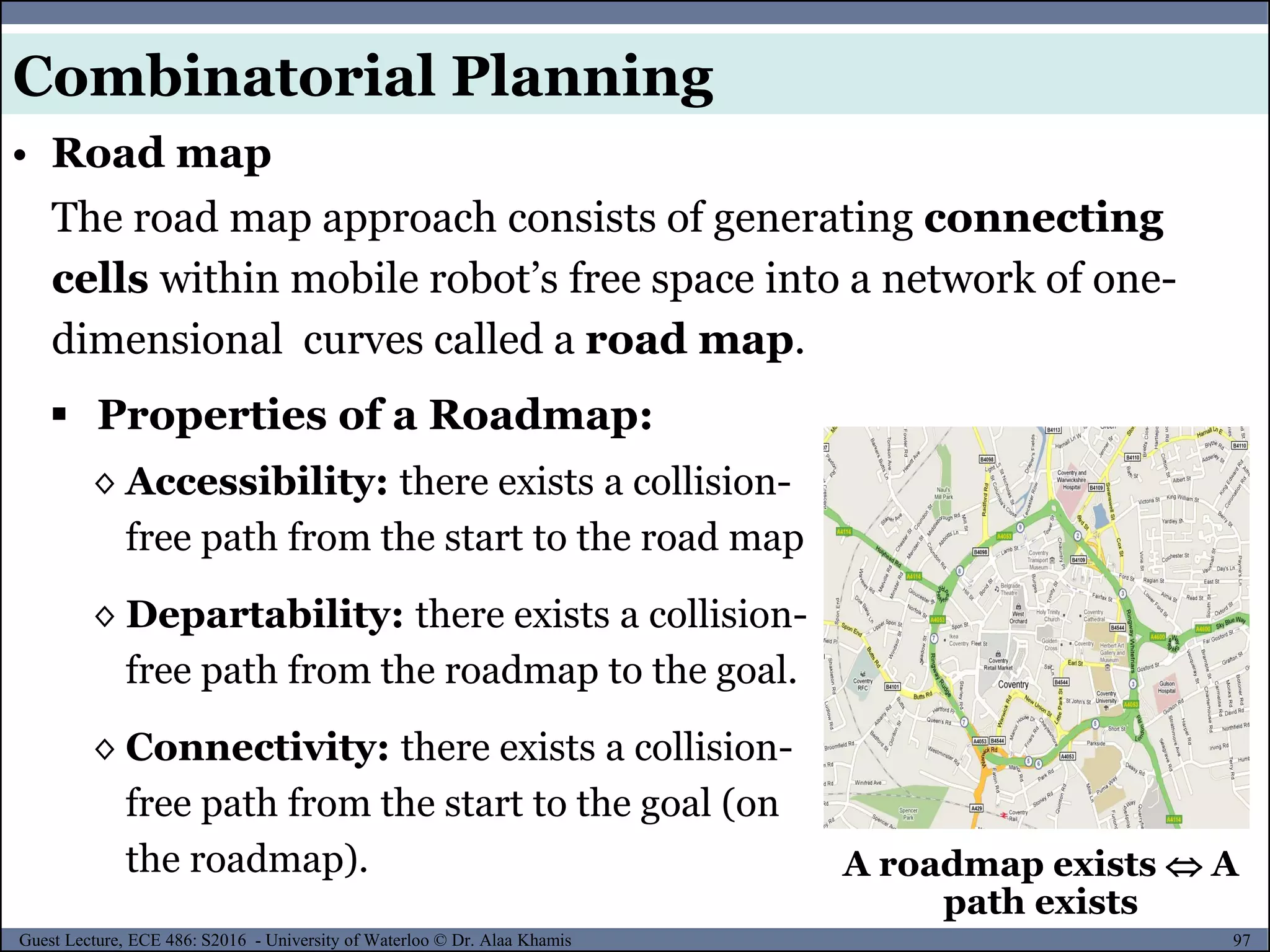








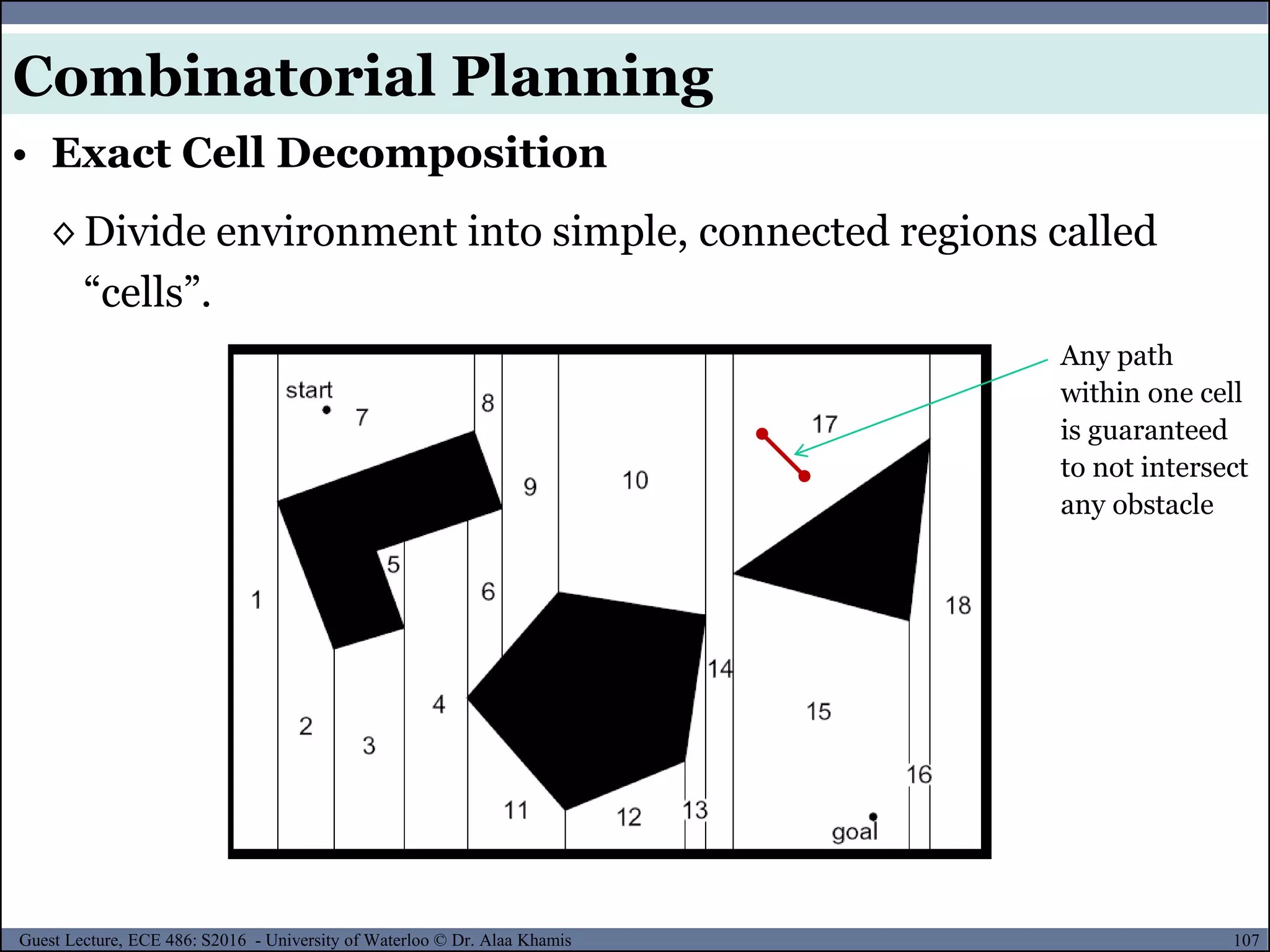














![122Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• The main idea of sampling-based motion planning is to avoid
the explicit construction of 𝒞obs, and instead conduct a search
that probes the C-space with a sampling scheme.
Sampling-based Motion Planning
Geometric
Models
Collision
Detection
Sampling-based Motion
Planning Algorithm
Discrete
Searching
C-Space
Sampling
[2]
• The sampling-based planning philosophy uses collision
detection as a “black box” that separates the motion planning
from the particular geometric and kinematic models.
• C-space sampling and discrete planning (i.e., searching) are
performed.](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-122-2048.jpg)
![124Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Sampling-based Motion Planning
• Probabilistic Roadmaps (PRMs)
Given: G(V,E) represents a
topological graph in which V is a
set of vertices and E is the set of
paths that map into 𝒞free.
Under the multiple-query philosophy, motion planning is
divided into two phases of computation:
Preprocessing/Learning Phase Query Phase
Build G in a way that is useful for
quickly answering future queries. For
this reason, it is called a roadmap,
which in some sense should be
accessible from every part of 𝒞free.
roadmap
query
(qinit,qgoal) pair
Path
[2]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-124-2048.jpg)
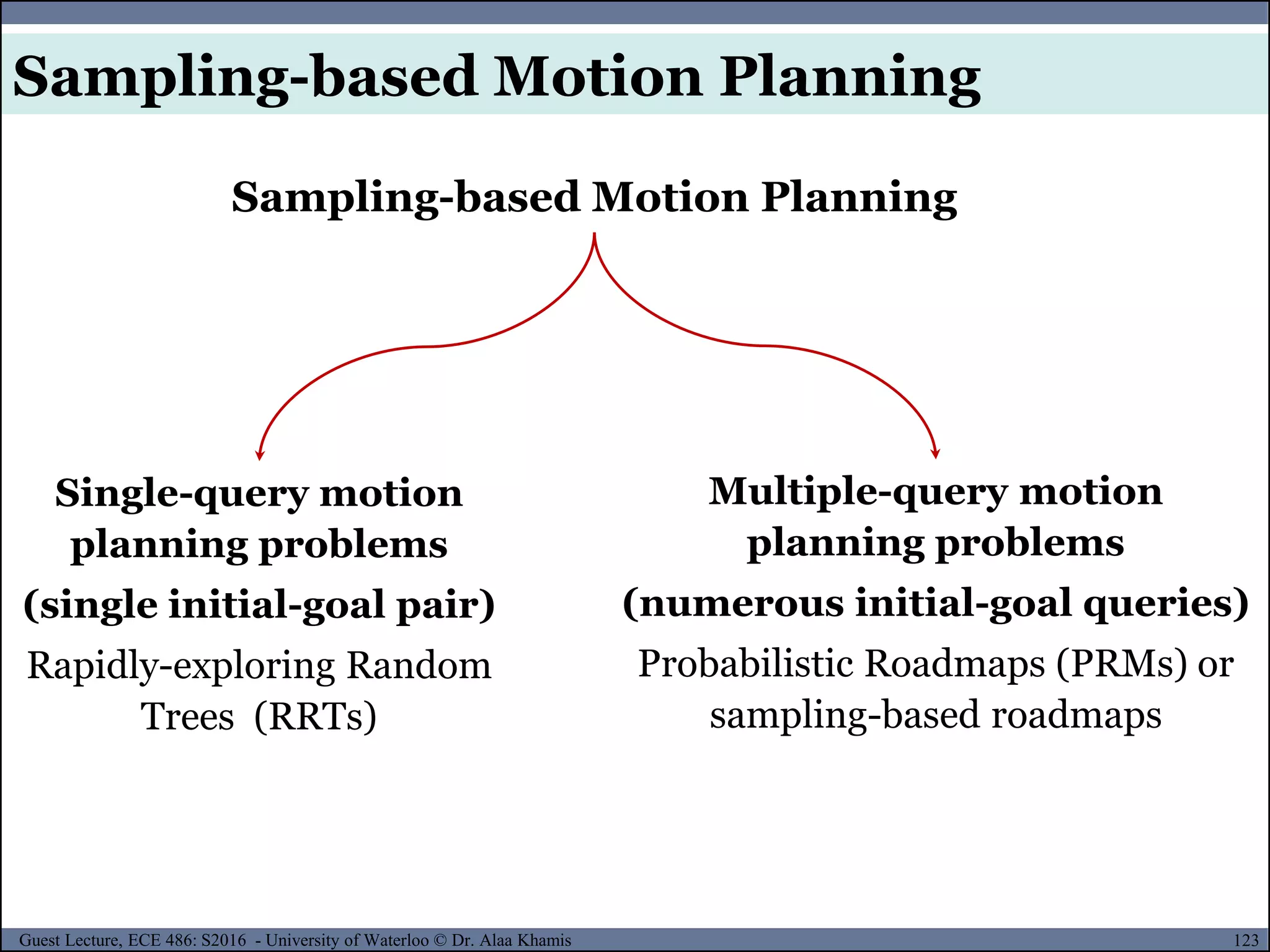
![125Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Sampling-based Motion Planning
• PRM: Preprocessing/Learning Phase
The sampling-based roadmap
is constructed incrementally by
attempting to connect each
new sample, (i), to nearby
vertices in the roadmap
Note that i is not incremented if (i) is in collision. This forces i
to correctly count the number of vertices in the roadmap.
[2]
Possible selection methods:
Nearest K;
Radius;
Visibility
…](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-125-2048.jpg)

![128Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Sampling-based Motion Planning
• PRM: Summary
a) A set of random sample is
generated in the configuration
space. Only collision-free samples
are retrained.
b) Each sample is connected to its
nearest neighbors using a simple,
straight-line path. If such a path
causes a collision, the
corresponding samples are not
connected in the roadmap
[4]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-128-2048.jpg)
![129Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Sampling-based Motion Planning
• PRM: Summary
c) Since the initial roadmap contains
multiple connected components,
additional samples are generated and
connected to the roadmap.
d) A path from qinit to qgoal is found by
connected qinit and qgoal to the
roadmap and then searching this
augmented roadmap for a path from
qinit to qgoal
[4]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-129-2048.jpg)












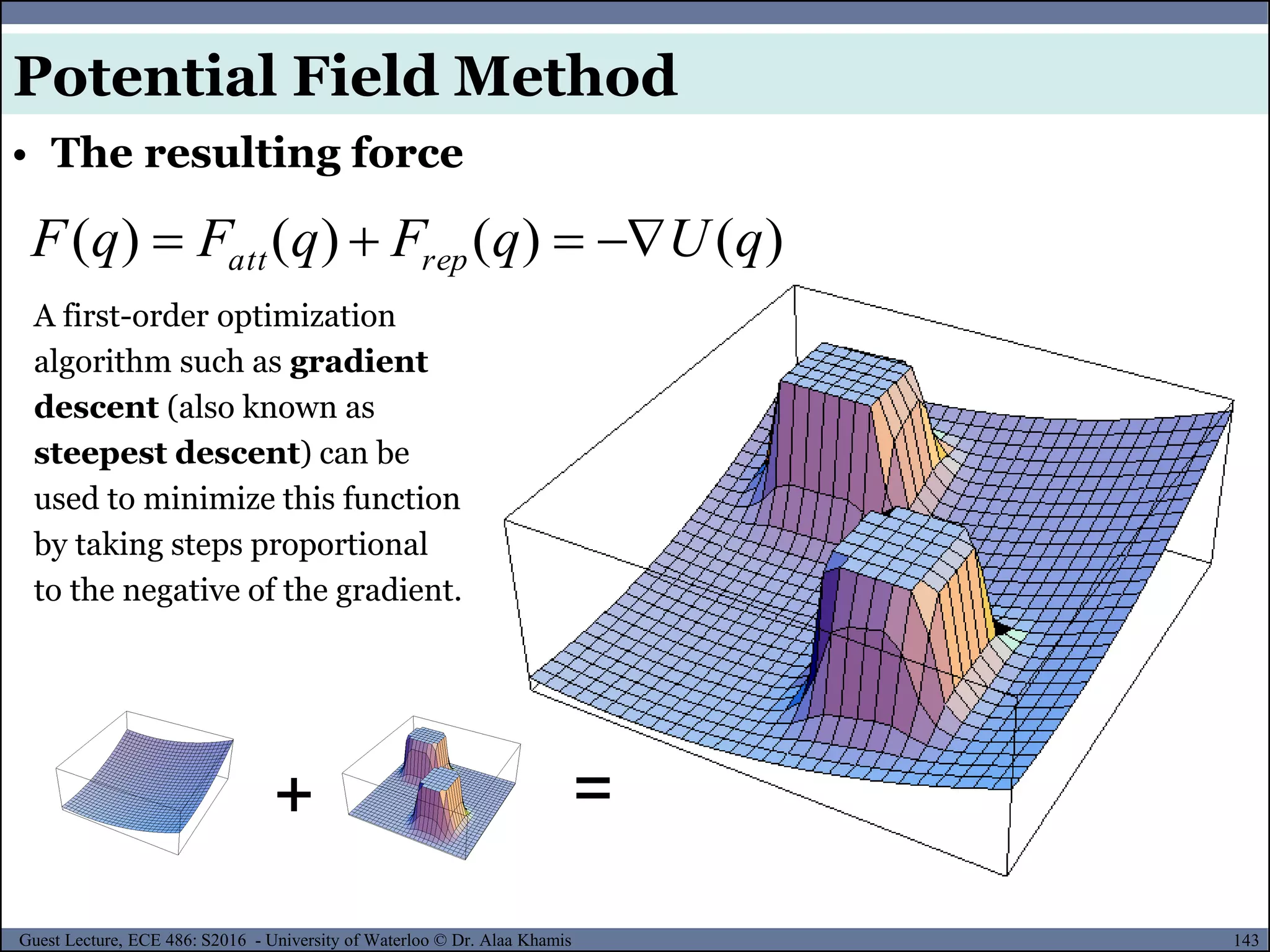







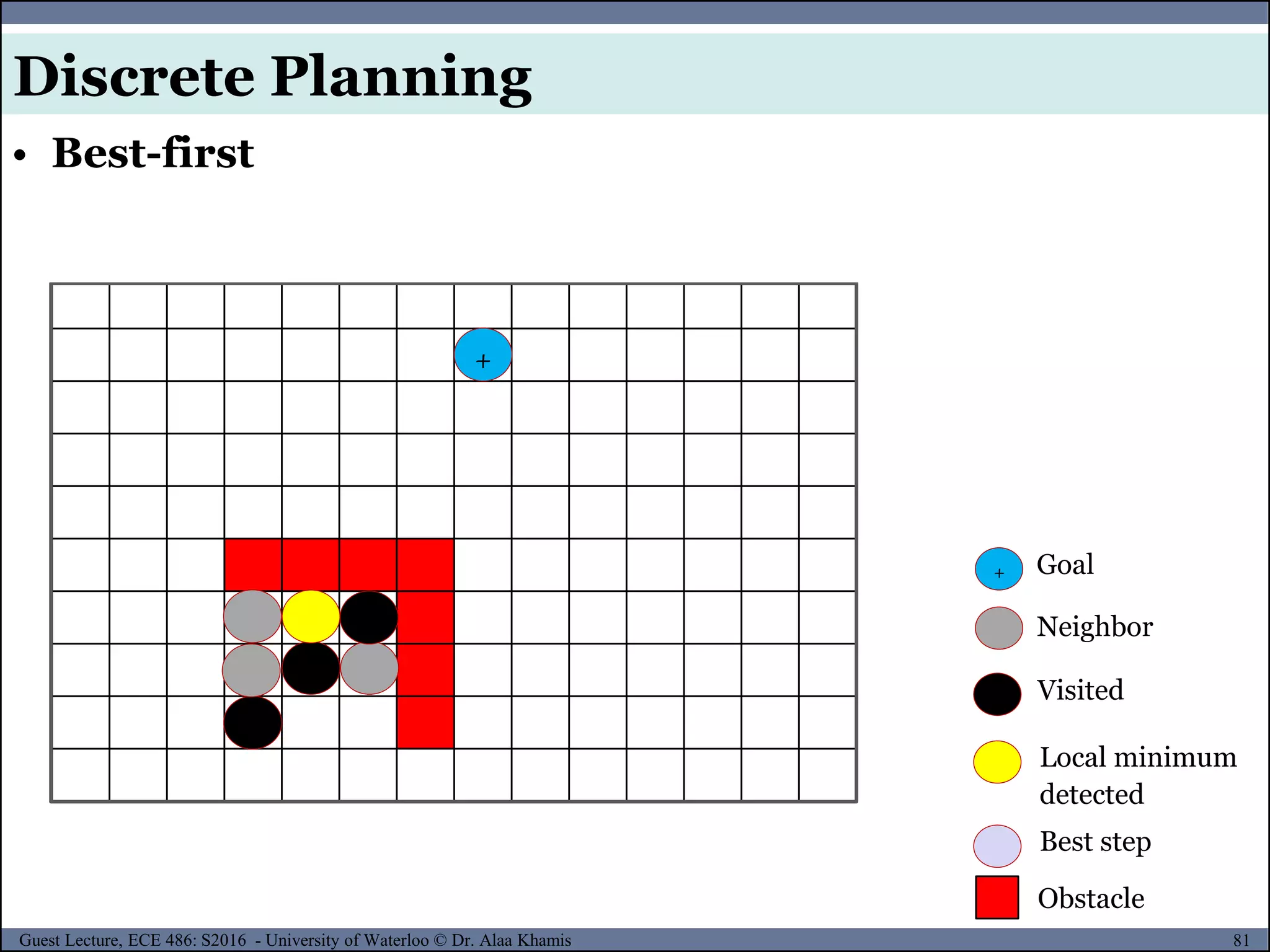
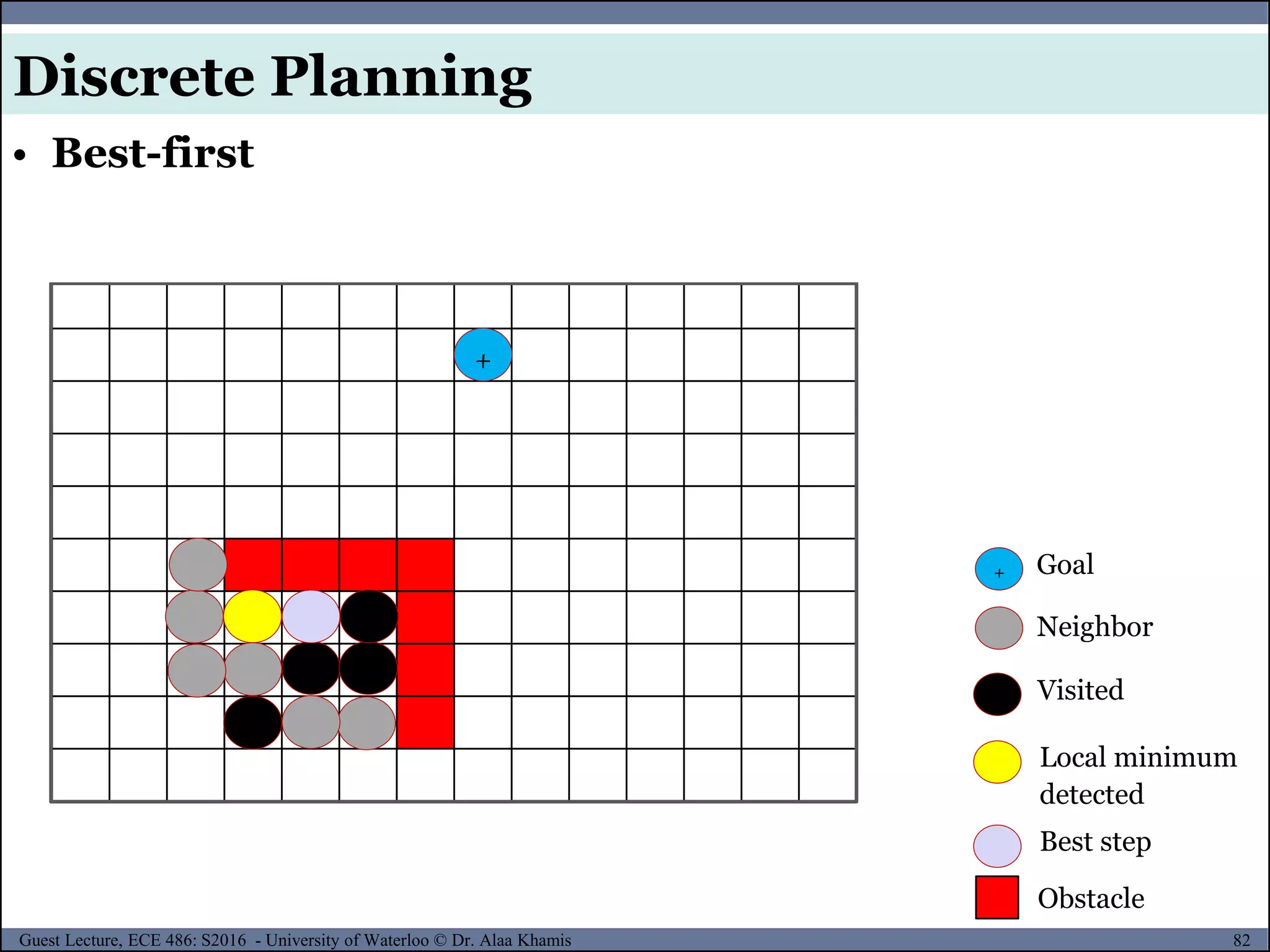
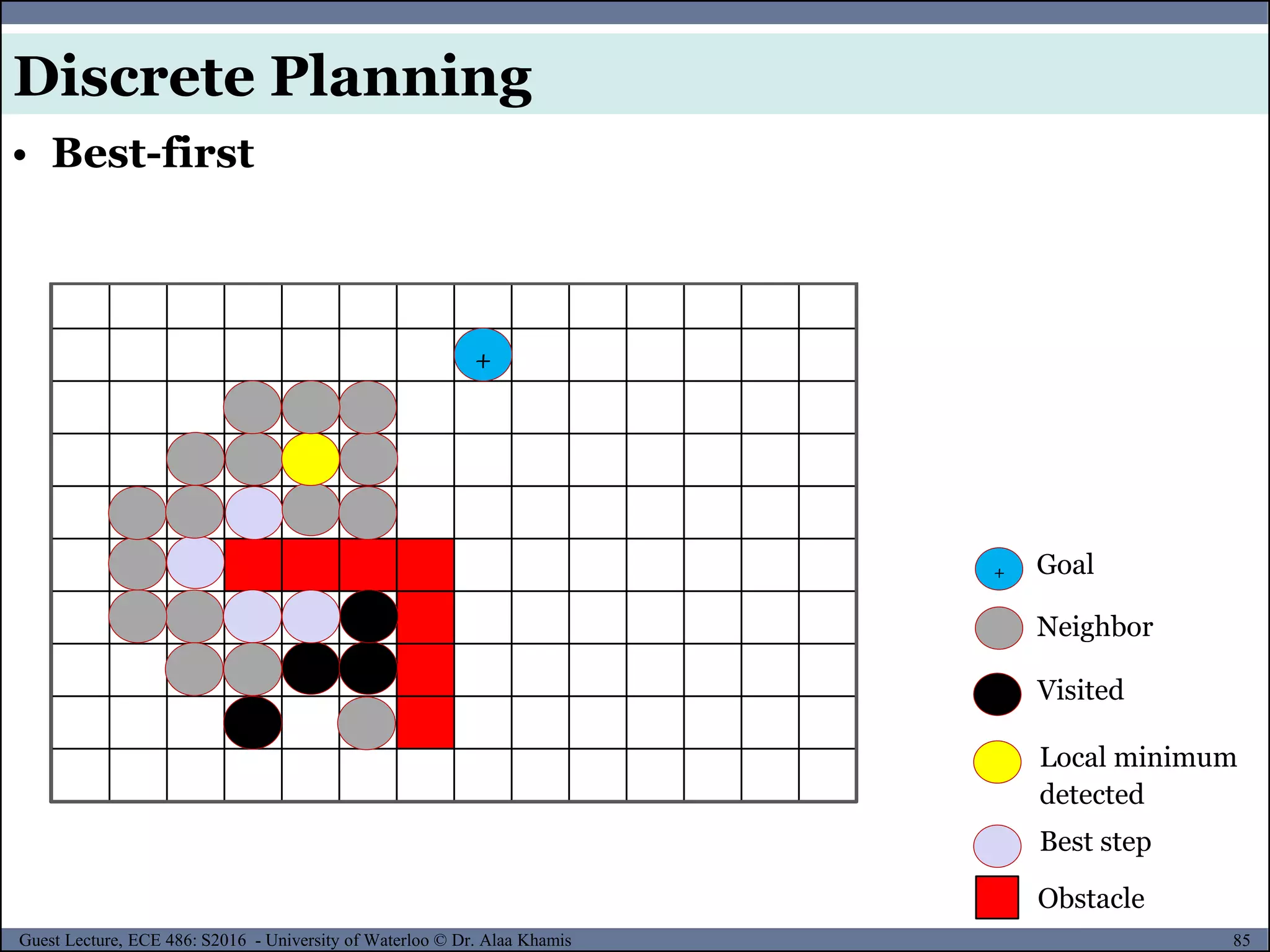
![151Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
The configuration qmin is a local minimum in the potential field.
At qmin the attractive force exactly cancels the repulsive fore and
the planner fails to make further progress.
• Problems of Potential Field Method
Potential Field Method
[4]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-151-2048.jpg)




![156Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
◊ A path is defined as the
collection of a sequence of
configurations a robot
makes to go from one place to
another without regard to the
timing of these
configurations.
Sequential robot movements in a path
◊ A trajectory is related to the timing at which each part of the
path must be attained.
◊ As a result, regardless of when points B and C in the figure are
reached, the path is the same, whereas depending on how fast
each portion of the path is traversed, the trajectory may differ.
Same Path Different
Trajectories
Trajectory Planning
• Path versus Trajectory
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-156-2048.jpg)
![157Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
◊ The points at which the robot may be on a path and on a
trajectory at a given time may be different, even if the robot
traverses the same points.
◊ On a trajectory, depending on the velocities and
accelerations, points B and C may be reached at different
times, creating different trajectories.
Sequential robot movements in a path
◊ In this lecture, we are not only concerned about the path a
robot takes, but also its velocities and accelerations.
Trajectory Planning
• Basics: Path versus Trajectory
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-157-2048.jpg)
![158Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Basics: Joint-space Motion Description
1000
zpzazozn
ypyayoyn
xpxaxoxn
6
5
4
3
2
1
θ
θ
θ
θ
θ
θ
Inverse Kinematics
Joint ValuesDesired End-effector Pose B
Joint Controllers
New Pose
B
◊ In this case, although the robot will eventually reach the
desired position, but as we will see later, the motion between
the two points is unpredictable.
◊ The joint values calculated using
inverse kinematics are used by the
controller to drive the robot joints to
their new values and, consequently,
move the robot arm to its new position.
Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-158-2048.jpg)
![159Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Sequential motions of a robot to follow a straight line
• Basics: Cartesian-space Motion Description
◊ Now assume that a straight line is drawn between points A
and B, and it is desirable to have the robot move from point A
to point B in a straight line.
◊ To do this, it will be necessary to divide the line into small
segments, as shown above and to move the robot through all
intermediate points.
Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-159-2048.jpg)
![160Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Basics: Cartesian-space Motion Description
◊ To accomplish this task, at each intermediate location, the
robot’s inverse kinematic equations are solved, a set of joint
variables is calculated, and the controller is directed to drive
the robot to those values. When all segments are completed,
the robot will be at point B, as desired.
◊ However, in this case, unlike the
joint-space case, the motion is
known at all times.
◊ The sequence of movements the
robot makes is described in
Cartesian-space and is converted
to joint-space at each segment.
Sequential motions of a robot to follow
a straight line
Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-160-2048.jpg)
![161Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Basics: Cartesian-space Motion Description
◊ Cartesian-space trajectories are very easy to visualize. Since
the trajectories are in the common Cartesian space in which we
all operate, it is easy to visualize what the end-effector’s
trajectory must be.
◊ However, Cartesian-space
trajectories are
computationally
expensive and require a
faster processing time
for similar resolution than
joint-space trajectories.
Sequential motions of a robot to follow
a straight line
Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-161-2048.jpg)
![162Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Basics: Cartesian-space Motion Description
◊ Although it is easy to visualize the trajectory, it is difficult to
visually ensure that singularities will not occur.
For example, consider the situation shown here.
◊ If not careful, we may specify a trajectory that requires the
robot to run into itself or to reach a point outside of the
work envelope—which, of course, is impossible-and yields
an unsatisfactory solution.
The trajectory specified
in Cartesian coordinates
may force the robot to
run into itself.
The trajectory may
require a sudden change
in the joint angles.
Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-162-2048.jpg)
![163Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Basics:
Given: a simple 2-DOF robot (mechanism)
Required:
2-DOF Mechanism
Move the robot from point A to point B.
Suppose that:
At initial point A: =200 & =300.
At final point B: =400 & =800.
Both joints of the robot can move at the maximum rate of 10
degrees/sec.
Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-163-2048.jpg)
![164Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Joint-space, Non-normalized Movements:
One way to move the robot from point A to B is to run both
joints at their maximum angular velocities. This means
that at the end of the second time interval, the lower link of the
robot will have finished its motion, while the upper link
continues for another three seconds, as shown here:
Joint-space, non-normalized movements of a 2-DOF Mechanism
The path is irregular, and
the distances traveled by the
robot’s end are not uniform.
Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-164-2048.jpg)
![165Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Basics: Joint-space, Normalized Movements
The motions of both joints of the robot are normalized such that
the joint with smaller motion will move proportionally slower so
that both joints will start and stop their motion simultaneously.
In this case, both joints move at different speeds, but move
continuously together. changes 4 degrees/second while
changes 10 degrees/second.
Joint-space, normalized movements of a 2-DOF Mechanism
The segments of the
movement are much more
similar to each other than
before, but the path is still
irregular (and different
from the previous case)
Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-165-2048.jpg)
![166Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Basics: Cartesian-space Movements
Now suppose we want the robot’s hand to follow a known path
between points A and B, say, in a straight line.
The simplest solution would be to draw a line between points A
and B, divide the line into, say, 5 segments, and solve for
necessary angles and at each point. This is called
interpolation between points A and B.
Cartesian-space movements of a 2-DOF Mechanism
The path is a straight line,
but the joint angles are not
uniformly changing.
Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-166-2048.jpg)
![167Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Basics: Cartesian-space Movements
◊ Although the resulting motion is a straight (and consequently,
known) trajectory, it is necessary to solve for the joint
values at each point.
◊ Obviously, many more points must be calculated for better
accuracy; with so few segments the robot will not exactly
follow the lines at each segment.
◊ This trajectory is in Cartesian-
space since all segments of the
motion must be calculated based
on the information expressed in a
Cartesian frame.
Cartesian-space movements
Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-167-2048.jpg)
![168Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Basics: Cartesian-space Movements
◊ In this case, it is assumed that the robot’s actuators are
strong enough to provide the large forces necessary to
accelerate and decelerate the joints as needed. For
example, notice that we are assuming the arm will be
instantaneously accelerated to have the desired velocity right
at the beginning of the motion in segment 1.
◊ If this is not true, the
robot will follow a
trajectory different
from our assumption; it
will be slightly behind as
it accelerates to the
desired speed.
Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-168-2048.jpg)
![169Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Basics: Cartesian-space Movements
◊ Note how the difference between two consecutive values is
larger than the maximum specified joint velocity of 10
degrees/second (e.g., between times 0 and 1, the joint must
move 25 degrees).
◊ Obviously, this is not attainable. Also note how, in this case,
joint 1 moves downward first before moving up.
Cartesian-space movements of a 2-DOF Mechanism
!!
Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-169-2048.jpg)

![171Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
◊ Trajectory planning with an acceleration/deceleration
regiment:
Of course, we still need to solve the inverse kinematic
equations of the robot at each point, which is similar to the
previous case.
However, in this case, instead of dividing the straight line AB
into equal segments, we may divide it based on x=(1/2).at2
until such time t when we attain the cruising velocity of v=at.
Similarly, the end portion of the motion can be divided based
on a decelerating regiment.
• Basics: Cartesian-space Movements
Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-171-2048.jpg)
![172Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
◊ Another variation to this trajectory planning is to plan a path
that is not straight, but one that follows some desired path,
for example a quadratic equation.
To do this, the coordinates of each segment are calculated based
on the desired path and are used to calculate joint variables at
each segment; therefore, the trajectory of the robot can be
planned for any desired path.
• Basics: Cartesian-space Movements
A case where straight line
path is not recommended.
Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-172-2048.jpg)



![177Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
◊ By solving these four equations simultaneously, we get the
necessary values for the constants. This allows us to calculate
the joint position at any interval of time, which can be
used by the controller to drive the joint to position. The same
process must be used for each joint individually, but they are
all driven together from start to finish.
◊ Applying this third-order polynomial to each joint motion
creates a motion profile that can be used to drive each joint.
3
2
1
2
32
3210
0010
1
0001
c
c
c
c
tt
ttt
θ
θ
θ
θ o
ff
fff
f
i
f
i
• 3rd Order Polynomial
Joint-Space Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-177-2048.jpg)

![179Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
◊ Example: It is desired to have the first joint of a 6-axis robot
go from initial angle of 30o to a final angle of 75o in 5 seconds.
Using a third-order polynomial, calculate the joint angle at 1, 2,
3, and 4 seconds.
◊ Given:
0)(
0)(
75)(
30)(
f
i
f
i
t
t
t
t
5
0
f
i
t
t
◊ Required:
4and1,2,3at t
• 3rd Order Polynomial
Joint-Space Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-179-2048.jpg)
![180Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
◊ Example (cont’d):
◊ Solution: Substituting the boundary conditions:
0)5(3)5(2)(
0)(
75)5()5()5()(
30)(
2
321
1
3
3
2
21
ccct
ct
cccct
ct
f
i
of
oi
032)(
0)(
)(
)(
2
321
1
3
3
2
21
fff
i
ffffof
ioi
tctcct
ct
tctctcct
ct
72.0,4.5,0,30 321 cccco
• 3rd Order Polynomial
Joint-Space Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-180-2048.jpg)
![181Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
◊ Example (cont’d): This results in the following cubic
polynomial equation for position as well as the velocity and
acceleration equations for joint 1:
tt
ttt
ttt
32.484.10)(
16.284.10)(
72.04.530)(
2
32
Substituting the desired time intervals into the motion
equation will result in:
oooo
32.70)4(,16.59)3(,84.45)2(,68.34)1(
• 3rd Order Polynomial
Joint-Space Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-181-2048.jpg)

![183Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
◊ Specifying the initial and ending positions, velocities, and
accelerations of a segment yields six pieces of information,
enabling us to use a fifth-order polynomial to plan a
trajectory, as follows:
3
5
2
432
4
5
3
4
2
321
5
5
4
4
3
3
2
21
201262)(
5432)(
)(
tctctcct
tctctctcct
tctctctctcct o
These equations allow us to calculate the coefficients of a fifth-
order polynomial with position, velocity, and acceleration
boundary conditions.
• 5th Order Polynomial
Joint-Space Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-183-2048.jpg)
![184Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
◊ Example: Repeat Example-1, but assume the initial
acceleration and final deceleration will be 5o/sec2.
2
2
/sec5/sec075
/sec5/sec030
o
f
o
f
o
f
o
i
o
i
o
i
Substituting in the following equations will result in:
◊ Solution: From Example-1 and the given accelerations, we
have:
3
5
2
432
4
5
3
4
2
321
5
5
4
4
3
3
2
21
201262)(
5432)(
)(
tctctcct
tctctctcct
tctctctctcct o
0464.058.06.1
5.2030
543
21
ccc
ccco
• 5th Order Polynomial
Joint-Space Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-184-2048.jpg)
![185Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
◊ Example (cont’d): This results in the following motion
equations:
32
432
5432
928.09.66.95)(
232.032.28.45)(
0464.058.06.15.230)(
tttt
ttttt
ttttt
Joint positions, velocities, and accelerations
• 5th Order Polynomial
Joint-Space Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-185-2048.jpg)
![186Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
◊ To ensure that the robot’s accelerations will not exceed its
capabilities, acceleration limits may be used to calculate the
necessary time to reach the target.
Joint positions, velocities, and
accelerations
In example-2:
The maximum acceleration is
8.7o/sec2< max
0and0For fi
2max
6
if
if
tt
8.10
05
30756
2max
sec/7.8max
o
• 5th Order Polynomial
Joint-Space Trajectory Planning
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-186-2048.jpg)

![188Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
• Cartesian-space trajectories relate to the motions of a robot
relative to the Cartesian reference frame, as followed by the
position and orientation of the robot’s hand.
• In addition to simple straight-line trajectories, many other
schemes may be deployed to drive the robot in its path between
different points.
• In fact, all of the schemes used for joint-space trajectory
planning can also be used for Cartesian-space trajectories.
• The basic difference is that for Cartesian-space, the joint values
must be repeatedly calculated through the inverse
kinematic equations of the robot.
Cartesian-Space Trajectories
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-188-2048.jpg)
![189Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
1. Increment the time by t=t+t.
2.Calculate the position and orientation of the hand
based on the selected function for the trajectory.
3.Calculate the joint values for the position and
orientation through the inverse kinematic equations of
the robot.
4.Send the joint information to the controller.
5.Go to the beginning of the loop.
• Procedure
Cartesian-Space Trajectories
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-189-2048.jpg)
![190Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
A 3-DOF robot designed for lab
experimentation has two links, each 9
inches long. As shown in the figure, the
coordinate frames of the joints are such
that when all angles are zero, the arm is
pointed upward.
The inverse kinematic equations of the robot are also given
below.
We want to move the robot from point (9,6,10) to point
(3,5,8) along a straight line.
Find the angles of the three joints for each intermediate point
and plot the results.
• Example
Cartesian-Space Trajectories
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-190-2048.jpg)
![191Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
Given:
13
3311
2
22
11
3
1
1
118
18
cosθ
162
1628/
cosθ
)/(tanθ
CC
SPCPC
PCP
PP
yz
zy
yx
Required:
Angles of the three joints for each intermediate point and plot
the results.
Inverse Kinematics Solution
B(3,5,8)A(9,6,10) linestraight
• Example (cont’d)
Cartesian-Space Trajectories
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-191-2048.jpg)

![193Guest Lecture, ECE 486: S2016 - University of Waterloo © Dr. Alaa Khamis
The inverse kinematic equations are used to calculate the
joint angles for each intermediate point, as shown in the
table.
The joint angles
are shown here.
Joint angles
• Example (cont’d)
Cartesian-Space Trajectories
[8]](https://image.slidesharecdn.com/motionplanning-171103002414/75/Motion-Planning-193-2048.jpg)
