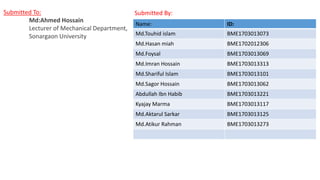
This document contains a presentation on vector analysis and matrices submitted by mechanical engineering students at Sonargaon University. It includes definitions of vectors, types of vectors, vector operations of addition, subtraction, dot product and cross product. It also defines different types of matrices, matrix operations of addition and subtraction, and scalar multiplication. Applications of vectors and matrices are discussed for calculating forces, velocities, and in cryptography to encrypt data for privacy.

1. Sonargaon University
Mechanical Department
BME0218-Sofia
A presentation of
“Vector Analysis & Matrix”

2. Submitted To:
Md:Ahmed Hossain
Lecturer of Mechanical Department,
Sonargaon University
Name: ID:
Md.Touhid islam BME1703013073
Md.Hasan miah BME1702012306
Md.Foysal BME1703013069
Md.Imran Hossain BME1703013313
Md.Shariful Islam BME1703013101
Md.Sagor Hossain BME1703013062
Abdullah Ibn Habib BME1703013221
Kyajay Marma BME1703013117
Md.Aktarul Sarkar BME1703013125
Md.Atikur Rahman BME1703013273
Submitted By:

3. Vector Analysis & Matrix

4. Vector
• A vector is a quantity having both magnitude and direction, such a displacement, velocity, force, and acceleration.
• A unit vector is a having unit magnitude, if A is a vector magnitude A≠0,then A/A is a unit vector having the same
direction as A.
Any vector A can be represented by a unit vector a in the direction A multiplied by the magnitude of A. In symbols,
A=Aa.
• Equal vector are those vector which have equal magnitude, same direction (parallel) and same sense (arrow).

5. • Zero vector or Null vector is that vector whose magnitude is zero.
• Addition of vector:
• A vector whose effect is the as set If of two vectors, is called the sum or the resultant of the given vectors.
let 𝑎 and 𝑏 two given vector. If 𝑂𝐴 = 𝑎 and 𝐴𝐵 = 𝑎 then the vector 𝑂𝐵 is called the sum of 𝑎 and 𝑏. Symbolically
𝑂𝐴+𝐴𝐵=𝑂𝐵
𝑎+ 𝑏=𝑂𝐵
• SUBTRACTION OF VECTORS
The subtraction of a vector 𝑎 vector 𝑏 from a is the addition of - 𝑏 to 𝑎.
𝑎- 𝑏= 𝑎+(- 𝑏)

6. • THE DOT OR SCALAR PRODUCT of two vectors A and B, denoted by A.B, is defined as the
product of the magnitude of A and B and the cosine of the angle between them.in
symbols,
A.B = A B cos𝜃
• THE CROSS OR VECTOR PRODUCT of A and B is a vector C=A×B.The magnitude of
A×B= 𝑨 𝑩 𝐬𝐢𝐧𝜽
• A× 𝑩 =
𝒊 𝒋 𝒌
𝑨𝟏 𝑨𝟐 𝑨𝟑
𝑩𝟏 𝑩𝟐 𝑩𝟑

7. Application Of Vector
• Force, torque, acceleration, velocity etc.
For calculating every vector unit, you need vector. For example, there is a tire with mass (m) and it has initial
and final velocity, acceleration, gravitational, reaction, friction forces and due to rotation it has torque. For
getting the result, you need vectors.
May be it seems like boring problem, but we need it in daily life, for instance finding velocity or acceleration of
cars. In construction, every architect have to know their buildings of durability, for this they need forces that
max how many force will apply to their building and of course they need again vectors. So you can see how the
vectors are important.

8. Matrices

9. The above system of numbers, arranged in a rectangular array in rows and columns
and bounded by brackets , is called a matrix.
Various Types Of Matrices:
(a)Row Matrix: If a matrix has only one row and any number of columns, its called
row matrix. e . g
[2 7 3 9]
(b) Column Matrix: A matrix, having one column and any number of rows, its called
column matrix. e . g
1
2
3
1
(C) Null Matrix/Zero Matrix: Any matrix, in which all the elements are zeros, is called
a zero matrix/ null matrix. e . g
0 0 0
0 0 0

10. (d) Square Matrix: A matrix, in which the number of rows is equal to the number of
columns, is called a square matrix. E . g
2 5
1 4
(e) Diagonal Matrix: A square matrix is called a diagonal matrix, if all its non-diagonal
elements are zero. E . g
1 0 0
0 3 0
0 0 4
(f) Unit/Identity Matrix: A square matrix is called a unit matrix if all the diagonal
elements are unity and non-diagonal elements are zero. E . g
1 0 0
0 1 0 , 1 0
0 0 1 0 1

11. (g) Transpose of a matrix: If a given matrix a, we interchange the row and the
corresponding columns, the new matrix obtained is called the transpose of the matrix
A and denoted by A’ or A e . g
a h g
h b f
g f c
(h) Singular matrix: It the determinant of the matrix is zero . then the matrix is know
is singular matrix. e.g.
If l A l = 1 2 = 6-6 =0,then A is a singular matrix.
3 6

12. ADDITION OF MATRICES:
If A and B be two matrices of the same order , then their sum , A+B is defined as the matrix,
each element of which is the sum of the corresponding elements of A and B.
Thus if
A= 4 2 5 B = 1 0 2
1 3 -6 , 3 1 4
Then A+B= 4 +1 2+0 5+2 = 5 2 7
1+3 3+1 -6+4 4 4 -2
SUBTRACTION OF MATRICES:
The difference of two matrices is a matrix , each element of which is obtained by subtracting
the elements of the second matrix from the corresponding element of the first.
A-B = aij- bij
Thus 8 6 4 ‒ 3 5 1
1 2 0 7 6 2
8 -3 6 -5 4 -1 = 5 1 3
1-7 2-6 0-2 -6 -4 -2

13. SCALAR MULTIPLE OF A MATRIX:
If a matrix is multiplied by a scalar quantity K, then each element is multiplied by K, i.e.
A = 2 3 4
4 5 6
6 7 9
3A=3 2 3 4 3*2 3*3 3*4 6 9 12
4 5 6 = 3*4 3*5 3*6 = 12 15 18
6 7 9 3*6 3*7 3*9 18 21 27

14. Application of matrix
• Cryptography is the process of encrypting data so that third party can’t read it and privacy
can be maintained.
• It was started with the TV cable industries where even people who were not the customer
could watch the TV programs.
• So, video cipher encryption system was invented which would convert signals into digital
form i. e .encrypt it, and the data were send over the satellite. The video cipher box would
decrypt the signal and those satellite dish owner who had video cipher box would receive
the decrypted signal i . e the original signal before encryption.
• In matrix same thing can be done.

15. THANK YOU