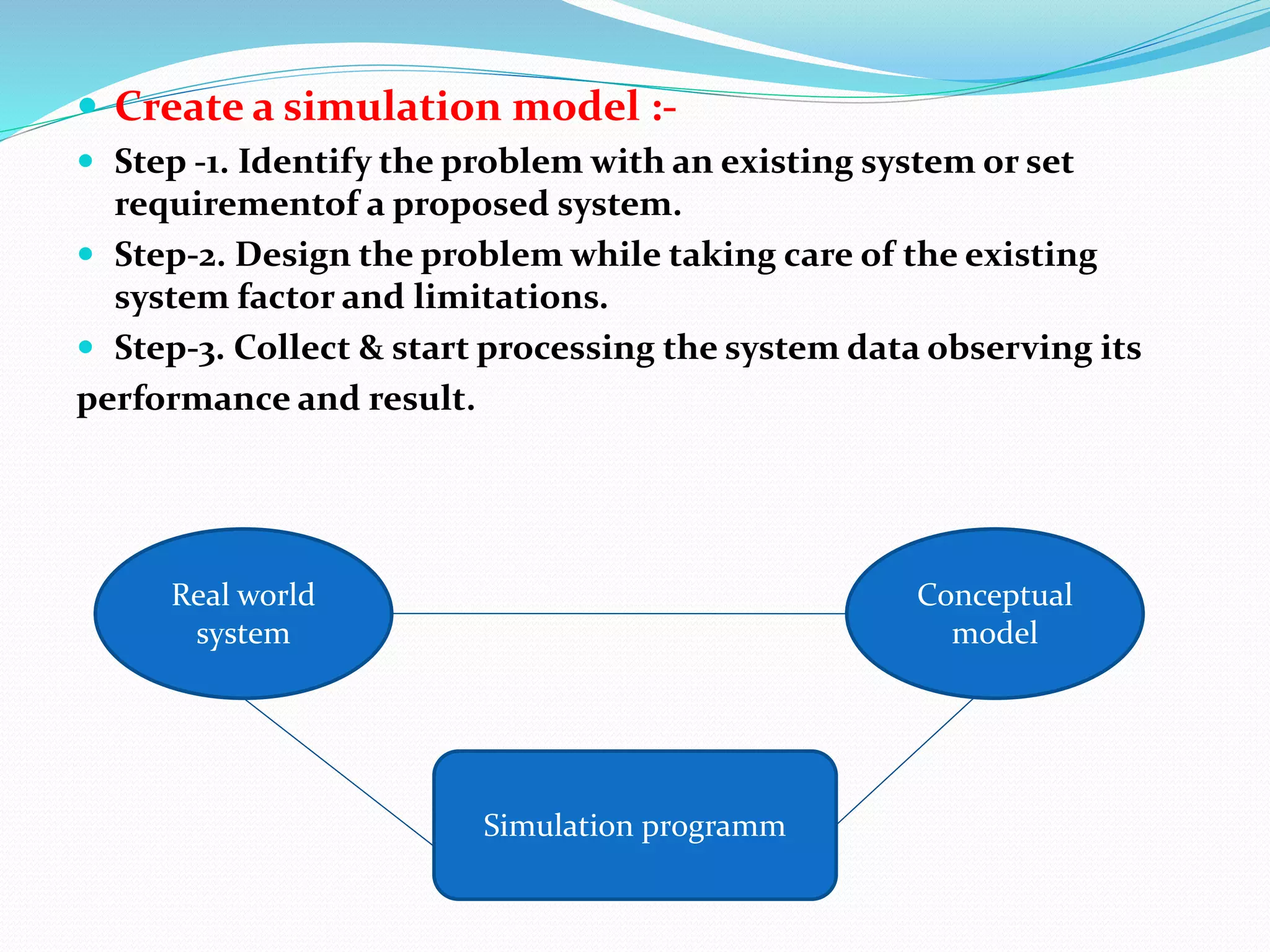
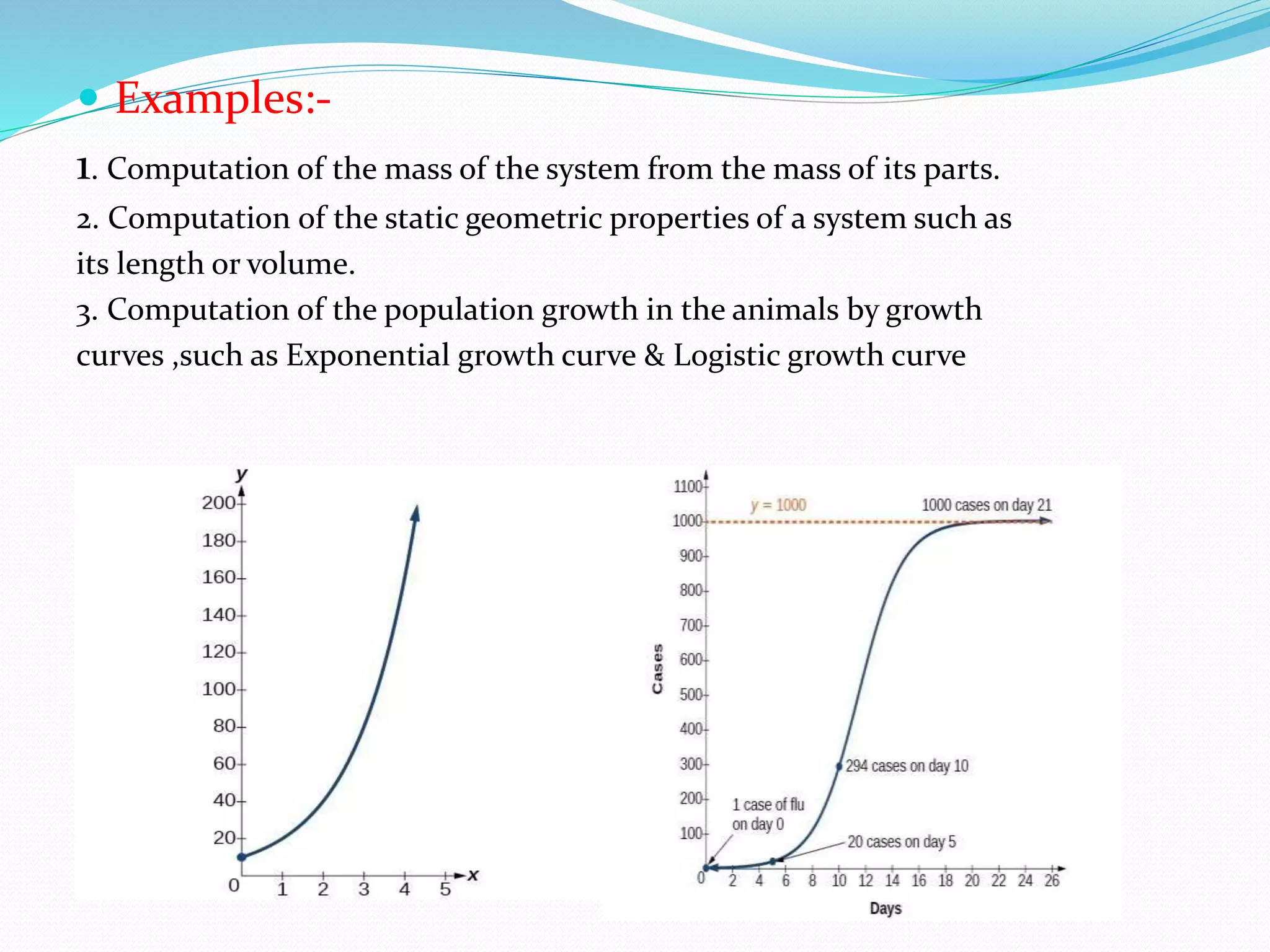
This document provides an overview of mathematical modeling. It defines mathematical modeling as using mathematical concepts and language to describe a system. The summary explains that mathematical modeling involves converting a real-world problem into a mathematical problem through interpretation, then deriving a mathematical solution and interpreting it back in terms of the real problem. It also discusses the key components, properties, types and examples of mathematical modeling, as well as its merits in fields like epidemiology, economics, and engineering. However, it notes that models are simplifications and may not replace reality.

1. UTTAM MEMORIAL COLLEGE PATELPALI
RAIGARH C. G.
Sub – quantitative biology
Topic – mathematical modelling
Guided by – sushmita sharma
Asst prof. Of zoology
Submitted by- nikita jaiswal
Msc. Zoology 1st sem

2. Synopsis:-
 1. Introductionn
 2. Definition
 3. Technique of mathematical modelling
 4. Principle of mathematical modelling
 5. Component of mathematical modelling
 6. Properties of mathematical modelling
 7. Types of mathematical modeling
 8. Explanation of modeling with Example
 9.Merits of mathematical modeling
 10.Demerits of mathematical modeling
 11.Conclusion
 12.Reference.

3. •Introduction:-
Mathematical model is a description of a
system using mathematical concepts and language. The
process of developing a mathematical model is termed
mathematical modeling. Mathematical models are used in the
natural sciences and engineering disciplines, as well as in nonphysical
systems such as the social sciences.
Through the mathematical modelling the real problem
of the a object or system is converted into a mathematical
model ,due to which the real problem gets solved easily. Many
problem such as interpretation of Tower’s height, interpretation
of River’s width, interpretation of earth’s weight etc.Their
solution can be done in a very simple way by mathematical modelling.

4. •Definition:-
 (1) “Mathematicalmodellingg is the process by which the
behaviour of an object and phenomenon is represented,
which is
based on the following mathematical language-
 1. Algebraic equation
 2. Differential equation
 3. Integral equation
 4. Algorithms
 5. Formulae
 6. Theorems.
 (2) “Mathematicall modeling is the process of using various
mathematical structures – graphs, equations, diagrams,
scatterplots, tree diagrams, and so forth – to represent real
world
situations”.

5. •Technique of mathematical modelling :-
The technique of mathematical modelling are very
important ,because by this process can be solved real world
problem, the technique of mathematical modelling in a
system
is as follows –
REAL PROBLEM
OBJESCT/ SYSTEM
INTERPRETATION
REAL PROBLEM
LANGUAGE
MATHEMATICAL
PROBLEM
MODELING PROCESS
MATHEMATICAL
SOLUTION
PREDICTION

6. In the technique, first the real problem of an object is
converted into a mathematical problem by modelling. In
the modelling process a model is created using
mathematical languages. Based on the mathematical
modelling a mathematical solution is derived, which is
based on the prediction and logic of that real problem.
The mathematical solution is explained in the language
of real problem which is called “Interpretation of
modelling” the formation of a model through any
specific technique
called “Modelling cycle” .

7. •Principle of Mathematical
modelling:-
 A model would be useful to understand the behaviour
of any system, as well as provide important information about
the system. Modelling is sequential and interactive process
that aids in simulation, analytical and statistics.
The Walters(1971) followed to 4 basic elements of
Mathematical modelling-
 1. System variables:-In this element the ‘Number of
sets’
present which represents the condition of the system.
 2. Functional relationship:-In this element ‘Model’s equation’
present ,which represent the interaction between a system and
their components.

8.  3. Fareing function:- It is an equation that represent
the input of the system.
 4. Parameters:- It element is on tank formula of
mathematical equation, which is assessed by the
model.
 SYSTEM VARIABLE
 FUNCTION RELATIONSHIP
 PARAMETER

9.  • Component of mathematical model:-
 1. Variable or decision parameter.
 2. Constant and calibration parameters.
 3. Input parameter.
 4. Output parameter.
 5. Data phase parameter.
 6. Noise and random parameter.
 • Properties of mathematical modelling:-
 (1) Realistic of Model- The mathematical model should always
be the one to
 show the reality, the more real the model, the more easily it can
be solved.
 (2) History of Model- The model represents any problem and
phenomenon
 more realistically.
 (3) Relatine precision of Model - The precision of different
models variable
 depending on the technique of its formation.

10.  (4) Robiatness of Model – Mathematical model Robiatness ,if
there is a
 slight change in their value, then there will be a change in the
real
 value.
 (5) Complication of Model – mathematical model are more
complicated
 . Because various relative mathematical point such as –Algebraic,
 Integral, Equations are used while preparing the model.
 (6) Choice of Model- All models give better and simple
mathematical
 . Results, but the same models is used ,which interpret the real
 problem.
 (7) Combination of Model- It is the property of modelling ,that
too small
 . models can be combined to form a complete mathematical
model.

11.  (8) Practical of Model – At the time of modeling ,first a
partial
 . model should be prepared for a sub-system, which should
 . be practical & test , then integrated into a cocomple
model.
 (9) Improvement of Model- There is a possibility of
improvement
 . in mathematical modelling ,So it can be improved on the
 . basis of practical and test.
 (10) Points of Model – The following points are essential for
 . preparing any mathematical model-
 . 1. Theories ,Technique & Practical.
 . 2. Real problem, structure & position.
 3. complete dictionary of mathematical modelling

12. • Type of mathematical
modelling:-
 1. Simulation modeling
 2. Analytical modeling
 3. Statistical modeling.
 1) Simulation Modelling –Mathematical simulation is an process to
identify and
predict the behaviour , performance & optimization of some physical or abstract
system corresponding to various scientific and engineering applications the
correct is mathematical Modeling and simulation. The simulation represent high
levels of abstraction and reproduce all features of real problem.
“Simulation is the process of model ,to study the behaviour and performance
of an actual or theoretical system. It's mostly mathematical and computerized.”
 Type of simulation:-1. Abstraction(Analytical).
 2. Heuristic (Algorithmic).
 3. Insilication(Computational).

13.  Create a simulation model :-
 Step -1. Identify the problem with an existing system or set
requirementof a proposed system.
 Step-2. Design the problem while taking care of the existing
system factor and limitations.
 Step-3. Collect & start processing the system data observing its
performance and result.
Real world
system
Conceptual
model
Simulation programm

14. 2) Analytical Modelling :-
Analytical models are mathematical models that have A
closed solution means the solution to the equation used to
describe changes in a system can been expressed as a
mathematical analytic function.
Analytical model is quantitative in nature, and used to
answer a specific question or make a specific design
decision.
Different analytical models are used to address different
aspects of the system, such as its performance, reliability, or
mass properties.
 Categories of analytical:-
 (a) Descriptive,(b) Diagnostic,(c) Predictive,(d) Prescriptiv

15.  Examples:-
1. Computation of the mass of the system from the mass of its parts.
2. Computation of the static geometric properties of a system such as
its length or volume.
3. Computation of the population growth in the animals by growth
curves ,such as Exponential growth curve & Logistic growth curve

16. 3) Statistical ModelIing:-
A statistical model is a mathematical model
that embodies a set of statistical assumption concerning the generation of
sample data. A Statistical model represents ofton in considerably
idealized
form the data generating process.
“Statistical model is a mathematical representation of observed data.”
Examples- logistic regression, time- series, clustering & decision
trees.
• Explanation of Mathematical Modelling with suitable Example
Equation and graphs are the most common type of mathematical
model. There are other type that fall into this category some of these
include pic-chart, tables, line-graph,chemical formulas or diagrams.

17. • Interpretation of Tower’s height:- The height of the tower can be
calculated with respect to some distance from the towers on the
ground and the angle made at that distance.

18. Merits of Mathematical modelling:-
 1) In Epidemiology- Mathematical modelling can be used to
understanding
how a virus spreads within a population. The essence of mathematical
modelling lies in writing down a set of mathematical equation that mimic
reality. These are then solve for certain values of the parameters within
the
equation.

19. 2) In Economic:-
Economists use models as the
primary tool for explaining or
making predictions about
economic issues and problems.

20. 3) Software development:-
Models are forms of description often
adoptedin software development.They
are abstractions used to represent and
communicate what is important.

21.  4) Financial industry engineering:-
The output of a financial model is
used for decision making and performing financial analysis,
whether
inside or outside of the company.
5) Optimal Business:- models are important for both new and
established businesses. They help new, developing companies
attract
investment, recruit talent, and motivate management and staff.
 6) Vehicular Traffic:- modelling plays an important part in
traffic
engineering. ... First is the traffic flows. In traffic flows, alternative
routes can be identified based on the number of vehicles. By using
the
simulation model, modeller can devise on how to reduce the levels
of

22. •Demerits of Mathematical
modelling:-
 1. The model is a simplification of the real problem and
does not include all aspects of the problems.
2. The model May only work in certain situations.
3. Model is idealization and can’t possibly replace reality.
4. Mathematical parameters are uncertain because they are
empirically determined.
5. The cost of running several different simulationsmay be
high.
6. Most models can't incorporate all the details of complex
natural phenomena & missing details.

23. • Conclusion:-
Mathematical models support our current concepts about
the population dynamics of resistance and can be useful tools
to quantitatively evaluate the relative contribution of
individual risk factors for resistance. As such they are
extremely valuable for the planning of future intervention
strategies.
The “Real world problem” is solved by mathematical model,
this is the reason that despite being mathematical, this
modelling plays on important role in biology.
 Reference:-
 . “ Fundamental of Ecological Modelling-
S.E.Jorgensen&G.Bendoricchio

24. THANKS FOR
WATCHING