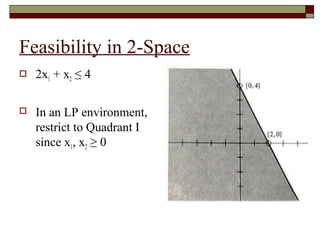
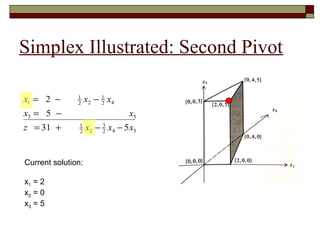
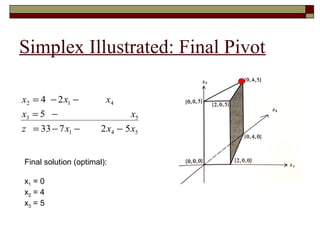
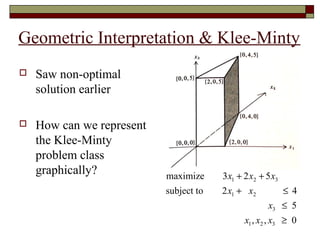
The document discusses the time complexity of the simplex algorithm for solving linear programming problems. It begins by defining time complexity as the number of arithmetic operations required to solve a problem. It then provides an overview of different time complexities such as polynomial time and exponential time. The rest of the document focuses on using geometric interpretations to understand the simplex algorithm and analyze cases where it exhibits exponential running time. It illustrates concepts like the region of feasibility and simplex pivoting through examples. It also reviews the Klee-Minty example, which shows that the simplex algorithm can require an exponential number of iterations in the worst case.

1. Time complexity of
simplex algorithm
Albi thomas
M.tech (TM)
Roll no.11

2. Introduction
 Time complexity of an algorithm counts the
number of arithmetic operations sufficient for
the algorithm to solve the problem
 Understand properties of LP in terms of
geometry
 Use geometry as aid to solve LP
 Some concepts new

3. Overview
 Polynomial time-complexity(bound)
Eg.gaussian elimination
 Exponential time complexity
Eg. Buchberger's algorithm
 Feasibility
 Simplex Method
 Simplex Weaknesses
 Exponential Iterations
 Convex Sets and Hulls

4. Region of Feasibility
 Graphical region describing all feasible
solutions to a linear programming problem
 In 2-space: polygon, each edge a constraint
 In 3-space: polyhedron, each face a constraint

5. Feasibility in 2-Space
 2x1 + x2 ≤ 4
 In an LP environment,
restrict to Quadrant I
since x1, x2 ≥ 0

6. Simplex Method
 Every time a new dictionary is generated:
 Simplex moves from one vertex to another vertex
along an edge of polyhedron
 Analogous to increasing value of a non-basic
variable until bounded by basic constraint
 Each such point is a feasible solution
 Average time taken is linear in 2 space

7. Feasibility in 3-Space
 maximize 3 x1 + 2 x2 + 5 x3
subject to 2 x1 + x2 ≤4
x3 ≤ 5
x1 , x2 , x3 ≥ 0
 Five total constraints;
therefore 5 faces to the
polyhedron

8. Simplex Illustrated: Initial Dictionary
x4 = 4 − 2 x1 − x2
x5 = 5 − x3
z = 3 x1 + 2 x2 + 5 x3
Current solution:
x1 = 0
x2 = 0
x3 = 0

9. Simplex Illustrated: First Pivot
x4 = 4 − 2 x1 − x2
x3 = 5 − x5
z = 25 + 3 x1 + 2 x2 − 5 x5
Current solution:
x1 = 0
x2 = 0
x3 = 5

10. Simplex Illustrated: Second Pivot
x1 = 2 − 1
2 x 2 − 1 x4
2
x3 = 5 − x5
z = 31 + 1
2 x2 − 3 x4 − 5 x5
2
Current solution:
x1 = 2
x2 = 0
x3 = 5

11. Simplex Illustrated: Final Pivot
x2 = 4 − 2 x1 − x4
x3 = 5 − x5
z = 33 − 7 x1 − 2 x4 − 5 x5
Final solution (optimal):
x1 = 0
x2 = 4
x3 = 5

12. Simplex Review and Analysis
 Simplex pivoting represents traveling along
polyhedron edges
 Each vertex reached tightens one constraint
(and if needed, loosens another)
 May take a longer path to reach final vertex
than needed

15. Simplex Weaknesses: Exponential
Iterations: Klee-Minty Reviewed
100 x1 + 10 x2 + x3 = z
x1 ≤ 1
20 x1 + x2 ≤ 100
200 x1 + 20 x2 + x3 ≤ 10, 000
x1 , x2 , x3 ≥ 0
 Cases with high complexity (2n-1 iterations)
 Normal complexity is O(m3)
 How was this problem solved?

16. Geometric Interpretation & Klee-Minty
 Saw non-optimal
solution earlier
 How can we represent
the Klee-Minty
problem class
graphically? maximize 3 x1 + 2 x2 + 5 x3
subject to 2 x1 + x2 ≤ 4
x3 ≤ 5
x1 , x2 , x3 ≥ 0

17. Step 1: Constructing a Shape
c1 x1 + c2 x2 + c3 x3 = z
 Start with a cube.
x1 ≤ 1
x2 ≤ 1
 What characteristics do x3 ≤ 1
we want the cube to x1 , x2 , x3 ≥ 0
have?
 What is the worst case
to maximize z?

18. Step 1: Constructing a Shape
 Goal 1: Create a shape
with a long series of
increasing facets
 Goal 2: Create an LP
problem that forces this
route to be taken

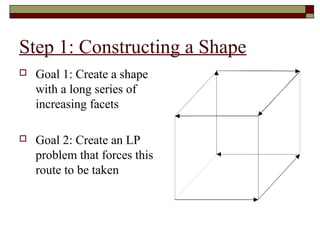
19. Step 2: Increasing Objective Function:
Modifying the Cube
[0, 1, 0.8] [0, 1, 0.82]
 Squash the cube
100 x1 + 1, 000 x2 + 10, 000 x3 = z
x1 ≤ 1
0.2 x1 + x2 ≤ 1 [0, 0, 1] [1, 0, 0.98]
0.02 x1 + 0.2 x2 + x3 ≤ 1
x1 , x2 , x3 ≥ 0
[0, 1, 0] [1, 0.8, 0]
 New dictionary
x4 = 1 − x1
x5 = 1 − 0.2 x1 − x2
x6 = 1 − 0.02 x1 − 0.2 x2 − x3 [1, 0, 0]
[0, 0, 0]

20. Step 3: Achieving 2n-1 Iterations:
Altering the Algebra
Let
sjxj = xj 100
x1
s1
+ 1, 000
x2
s2
+ 10, 000
x3
s3
= z
s1 1
x1 ≤
s4 s4
Convert s1 s2 1
z = v + ∑ d jxj 0.2 x1
s5
+
s5
x2 ≤
s5
j∈N s1 s2 s3 1
0.02 x1 + 0.2 x2 + x3 ≤
s6 s6 s6 s6
to x1 , x2 , x3 ≥ 0
z = v + ∑ (d j s j ) x j
j∈N

21. The Final Solution
 Most desirable: x1 , x4
 Least desirable: x3
s1 = s4 = 1, s2 = s5 = 0.01, s3 = s6 = 0.0001
100 x1 + 10 x2 + x3 = z
x1 ≤ 1
20 x1 + x2 ≤ 100
200 x1 + 20 x2 + x3 ≤ 10, 000
x1 , x2 , x3 ≥ 0

22. Thank you