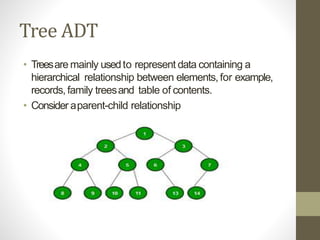
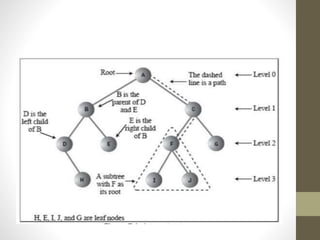
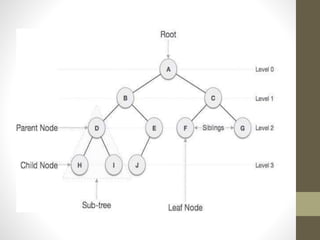
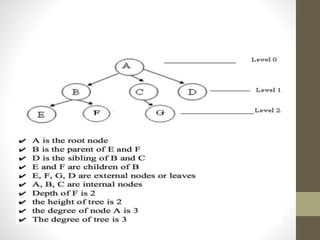
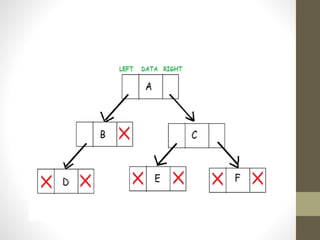
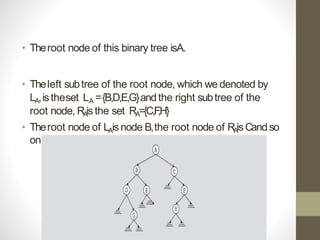
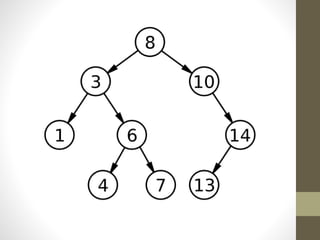
Trees are hierarchical data structures used to represent data with parent-child relationships. A tree has a root node with child nodes, and each non-root node has one parent. Trees allow fast search, insertion, and deletion similar to linked lists but can also maintain ordering like arrays. Binary trees restrict nodes to at most two children, enabling efficient search, storage of expressions, and routing algorithms. Binary search trees organize nodes to enable fast lookups based on key values.

1. UNIT 3 - TREES

2. Tree ADT
• Treesare mainly usedto represent data containing a
hierarchical relationship between elements, for example,
records, family treesand table of contents.
• Consider aparent-child relationship

3. • Treeis asequence of nodes
• There is astarting node known asaroot node
• Everynode other than the root hasaparentnode.
• Nodes mayhaveany number of children

6. Key terms
• Root−Node at the top of the treeiscalled root.
• Parent −Anynode except root node hasone edgeupward to anode called parent.
• Child−Node below agiven node connected by its edgedownward is called its child
node.
• Sibling– Childof samenode are calledsiblings
• Leaf−Node which does not haveanychild node is called leaf node.
• Subtree −Subtree represents descendants of anode.
• Levels−Levelof anode represents the generation of anode. If root node is at level
0, then itsnext child node isat level 1, its grandchild isat level 2 and soon.
• keys−Keyrepresents avalue of anode basedon which asearch operation is to be
carried out for anode.

7. • Degreeof anode:
• Thedegree of anode isthe number of children of that node
• Degreeof aTree:
• Thedegree of atree isthe maximum degree of nodes in agiventree
• Path:
• It isthe sequenceof consecutive edgesfrom sourcenode to
destination node.
• Height of anode:
• Theheight of anode isthe maxpath length form that node to aleaf
node.
• Height of atree:
• Theheight of atree isthe height ofthe root
• Depth of atree:
• Depth of atree isthe maxlevel of anyleaf in the tree

9. Characteristicsof trees
• Non-linear datastructure
• Combinesadvantagesof anordered array
• Searchingasfast asin ordered array
• Insertion and deletion asfast asin linked list
• Simple and fast

10. Applications
• Directory structure of afilestore
• Structure of an arithmeticexpressions
• Usedin almost every 3Dvideo gameto determine
what objects need tobe rendered.
• Usedin almost every high-bandwidth router for storing
router-tables.
• used in compression algorithms, suchasthose used by the
.jpeg and .mp3 file- formats.

11. Tree Traversal
• Traversalis aprocessto visit all the nodes of atree
and mayprinttheir values too.
• All nodes are connected via edges(links) we always
start from theroot (head) node.
• There are three wayswhich we useto traverse atree
• In-orderTraversal
• Pre-orderTraversal
• Post-orderTraversal
• Generally we traverse atree to search or locate given item
or keyin the tree or to print all the values it contains.

12. Pre-order,In-order,Post-order
• Pre-order
• <root><left><right>
• In-order
• <left><root><right>
• Post-order
• <left><right><root>

13. Pre-orderTraversal
• Thepreorder traversal of anonempty binary tree
is defined asfollows:
• Visit the root node
• Traversethe left sub-tree inpreorder
• Traversethe right sub-tree inpreorder

14. In-ordertraversal
• Thein-order traversal of anonempty binary tree is
defined asfollows:
• Traversethe left sub-tree inin-order
• Visit the root node
• Traversethe right sub-tree ininorder
• Thein-order traversal output of the given treeis
• H D I B E A F C G

15. Post-ordertraversal
• Thein-order traversal of anonempty binary tree is
defined asfollows:
• Traversethe left sub-tree inpost-order
• Traversethe right sub-tree inpost-order
• Visit
• Thein-order traversal output of the given treeis
• H I D E B F G C A
• the root node

16. Binary Trees
• Abinary tree, isatree in which no node canhave
more thantwo children.
• Consider abinary tree T
,here ‘A’isthe root node of the
binary treeT
.
• ‘B’ isthe left child of ‘A’and
‘C’istheright child of ‘A’
• i.eAisafather of BandC.
• Thenode BandCarecalled siblings.
• NodesD,H,I,F
,Jare leafnode

18. • Theroot node of this binary tree isA.
• Theleft subtree of the root node, which we denoted by
LA,istheset LA ={B,D,E,G}andthe right subtree of the
root node, RA
isthe set RA={C,F
,H}
• Theroot node of LAisnode B,the root node of RA
isCandso
on

19. BinaryTreeProperties
• If abinary tree contains m nodesat level L,it contains
atmost 2m nodes at levelL+1
• Sinceabinary tree cancontain at most 1 node at level 0
(the root),it contains at most 2Lnodesat levelL.

20. Typesof BinaryTree
• Complete binary tree
• Strictly binary tree
• Full binary tree
• Perfect binary tree
• Balanced binary tree
• Degenerate binary tree

21. Strictly binarytree
• If every non-leaf node in abinary tree hasnonempty leftandright sub-
trees,then suchatree iscalled astrictly binarytree.
• Or,to put it anotherway,all of the nodesin astrictly binary tree areof
degreezero or two, never degreeone.
• Astrictly binary tree with
• Nleavesalwayscontains 2N–1 nodes.

22. Completebinarytree
• Acomplete binary tree is a binary tree in which every
level, except possibly the last, is completely
• filled, and all nodes are asfar left aspossible.
• Acomplete binary tree of depth d is called strictly binary
tree if all of whose leaves are at level d.
• Acomplete binary tree has2d nodes at every depthd and
2d -1 non leaf nodes

23. Full binary tree
• It is a special kind of a binary tree that has either zero children or
two children. It means that all the nodes in that binary tree
should either have two child nodes of its parent node or the
parent node is itself the leaf node or the external node.
• In other words, a full binary tree is a unique binary tree where
every node except the external node has two children. When it
holds a single child, such a binary tree will not be a full binary
tree. Here, the quantity of leaf nodes is equal to the number of
internal nodes plus one. The equation is like L=I+1, where L is the
number of leaf nodes, and I is the number of internal nodes.

24. Perfect binary tree
• A binary tree is said to be ‘perfect’ if all the internal nodes
have strictly two children, and every external or leaf node is at
the same level or same depth within a tree. A perfect binary
tree having height ‘h’ has 2h – 1 node. Here is the structure of
a perfect binary tree

25. Balanced Binary Tree
• A binary tree is said to be ‘balanced’ if the tree height is
O(logN), where ‘N’ is the number of nodes. In a balanced
binary tree, the height of the left and the right subtrees of
each node should vary by at most one.
• An AVL Tree and a Red-Black Tree are some common examples
of data structure that can generate a balanced binary search
tree. Here is an example of a balanced binary tree

26. Degenerate Binary Tree
• A binary tree is said to be a degenerate binary tree or
pathological binary tree if every internal node has only a single
child.
• Such trees are similar to a linked list performance-wise. Here
is an example of a degenerate binary tree:

27. Benefits of a Binary Tree
• The search operation in a binary tree is faster as
compared to other trees
• Only two traversals are enough to provide the elements
in sorted order
• It is easy to pick up the maximum and minimum
elements
• Graph traversal also uses binary trees
• Converting different postfix and prefix expressions are
possible using binary trees

28. Expression Trees
• An Expression tree is a binary tree in which the operators are
stored in the interior nodes and the operands are stored in
the exterior nodes which are the leaves
• Construction of Expression Tree:
• 1) If character is operand push that into stack
2) If character is operator pop two values from stack make
them its child and push current node again.
At the end only element of stack will be root of expression
tree.
• https://www.techiedelight.com/expression-tree/

29. Applications of Trees
1) Manipulate hierarchical data
2) Make information easy to search
3) Manipulate sorted lists of data
4) Router algorithms
5) Form of a multi-stage decision-making, like Chess Game

30. BinarySearchTree(BST)
• Abinary search tree (BST)is a binary tree that is either
empty or in which every node contains a key (value)
and satisfies the following conditions:
• All keys in the left sub-tree of the root are smaller than
the key in the root
• node
• All keysin the right sub-tree of the root are greater than the
keyin the root node
• Theleft and right sub-trees of the root are againbinary
search trees

32. WhyBinarySearchTree?
• Some maythink of usingalinked list becauseit permits
insertion and deletion to be carried outby adjusting only
few pointers.
• But in ann-linked list, there isno wayto move through
thelist other than one node at atime, permitting only
sequentialaccess.
• Binary trees provide anexcellent solution to this problem.
Bymaking the entries of anordered list into the nodes of a
binary searchtree, we find that we cansearchfor akeyin
O(logn)

33. Insertion,Deletion,Search
• https://www.codesdope.com/course/data-structures-binary-
search-trees/
• https://www.codespeedy.com/insertion-and-deletion-in-a-
binary-search-tree-in-python/

34. Threaded binary trees
• Threaded binary tree is a simple binary tree but they have a
speciality that null pointers of leaf node of the binary tree is
set to inorder predecessor or inorder successor.
• https://www.youtube.com/watch?v=ffgg_zmbaxw
• Operations:
• Insert
• Search
• Delete

35. Applications
• To make inorder traversal of the binary tree faster and do it
without using any extra space, so sometimes in small systems
where hardware is very limited we use threaded binary tree
for better efficiency of the software in a limited hardware
space.