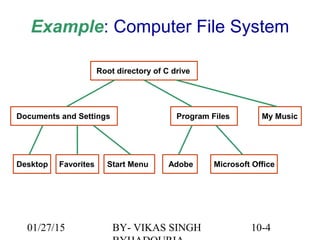
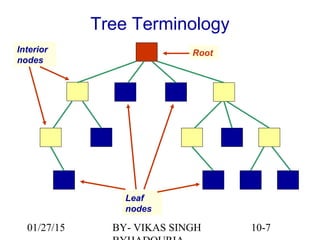
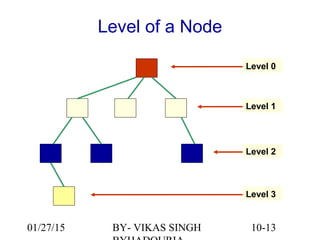
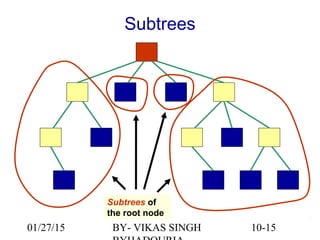
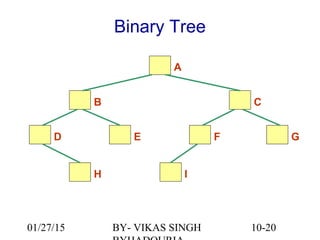
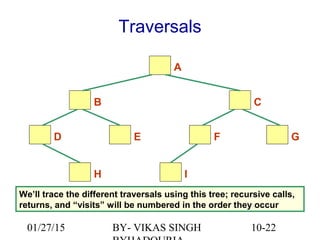
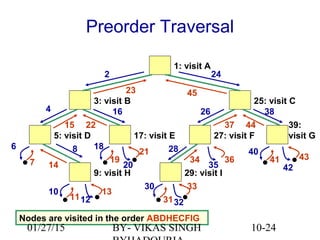
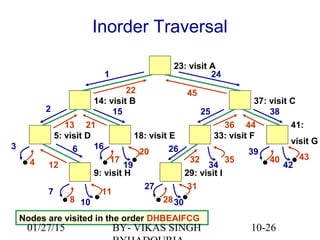
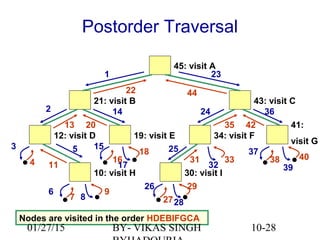
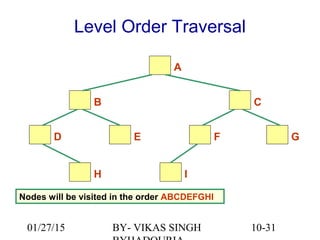
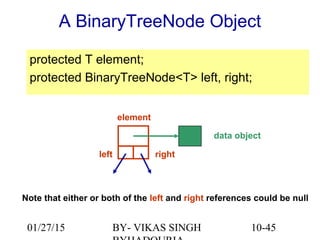
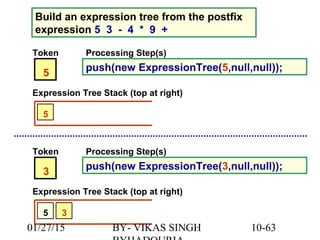
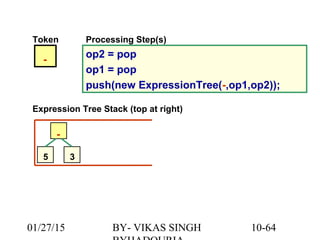
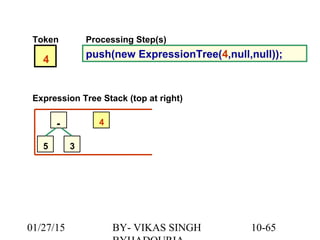
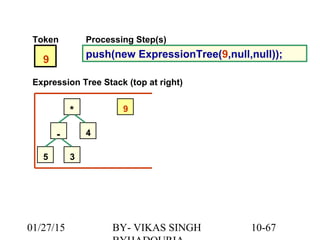
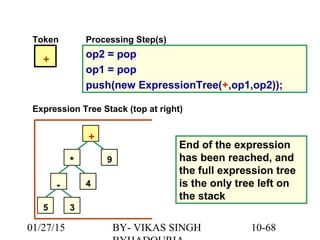
The document provides an overview of binary trees, defining key concepts such as nodes, edges, root, leaf nodes, and traversal algorithms. It outlines tree structures and their hierarchical nature, focusing on binary trees, which have a maximum of two children per node, and details various traversal methods including preorder, inorder, postorder, and level-order. Additionally, the document discusses common operations performed on binary trees, including adding and removing elements, and presents a linked binary tree implementation.