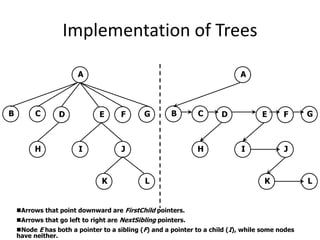
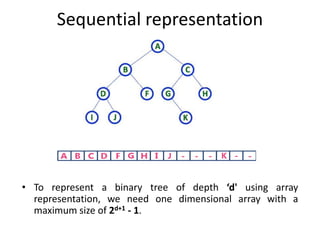
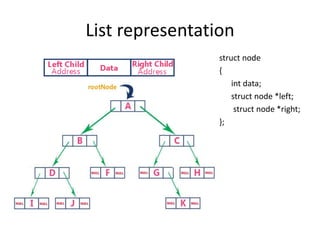
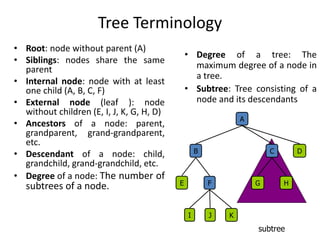
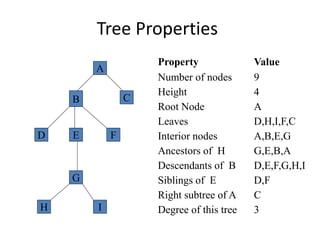
1. Trees are non-linear data structures that represent hierarchical relationships. They consist of nodes connected by edges, with one node designated as the root. 2. Trees can be represented using arrays or linked lists. Array representation requires knowing the height of the tree in advance, while linked lists do not waste memory but have slower access times. 3. Common tree terminology includes root, leaf nodes, internal nodes, siblings, ancestors, descendants, depth, height, and subtrees. Binary trees restrict nodes to at most two children each.

1. NON LINEAR DATA STRUCTURES
– TREES
B.Vijayalakshmi,AP(SG)/CSE
Ramco Institute of Technology,
Rajapalayam

2. Nature View of a Tree
branches
leaves
root

3. Computer Scientist’s View
branches
leaves
root
nodes

4. TREES
• Trees are one of the important non- Linear data
structure.
• A tree is a Multilevel data structure that represent a
hierarchical relationship between the Set of
individual elements called nodes.
• Each tree structure starts with a node Which is called
the root node of the Tree.

5. Tree- Definition
• A tree is a collection of nodes. The collection can be
empty; otherwise, a tree consists of a distinguished
node r, called the root, and zero or more non-empty
(sub) trees T1, T2, …, Tk each of whose roots are
connected by a directed edge from r.
• A tree is a collection of N nodes, one of which is the
root and N-1 edges.
Source:Mark Allen Weiss

6. Tree terminology
• The root of each subtree is said to be a child
of r and r is said to be the parent of each
subtree root.
• Leaves: nodes with no children (also known as
external nodes)
• Internal Nodes: nodes with children
• Siblings: nodes with the same parent
Source:Mark Allen Weiss - edited by Evan Korth

7. Tree terminology (continued)
• A path from node n1 to nk is defined as a sequence of
nodes n1, n2, …, nk such that ni is the parent of ni+1
for 1<= i <= k.
• The length of this path is the number of edges on
the path namely k-1.
• The length of the path from a node to itself is 0.
• There is exactly one path from the root to each node.
Source:Mark Allen Weiss

8. Tree terminology (continued)
• Depth of node is the length of the unique
path from the root to a node.
– Root is at depth 0.
• Depth (of tree): The depth of a tree is equal to
the depth of its deepest leaf.
• Height of node is the length of the longest
path from a node to a leaf.
• All leaves have a height of 0
• The height of a tree is equal to the height of
the root.
• The height of the root is equal to the depth of
the tree
Source:Mark Allen Weiss

9. Tree terminology (continued)
• Level number Every node in the tree is
assigned a level number in such a way that the
root node is at level 0, children of the root
node are at level number 1.
• Forests- A forest is a disjoint union of trees. A
set of disjoint trees (or forests) is obtained by
deleting the root and the edges connecting
the root node to nodes at level 1.

10. subtree
Tree Terminology
• Root: node without parent (A)
• Siblings: nodes share the same
parent
• Internal node: node with at least
one child (A, B, C, F)
• External node (leaf ): node
without children (E, I, J, K, G, H, D)
• Ancestors of a node: parent,
grandparent, grand-grandparent,
etc.
• Descendant of a node: child,
grandchild, grand-grandchild, etc.
• Degree of a node: The number of
subtrees of a node.
A
B DC
G HE F
I J K
• Degree of a tree: The
maximum degree of a node in
a tree.
• Subtree: Tree consisting of a
node and its descendants

11. Tree Properties
A
B C
D
G
E F
IH
Property Value
Number of nodes 9
Height 4
Root Node A
Leaves D,H,I,F,C
Interior nodes A,B,E,G
Ancestors of H G,E,B,A
Descendants of B D,E,F,G,H,I
Siblings of E D,F
Right subtree of A C
Degree of this tree 3

12. Implementation of Trees
• One way to implement a tree would be to have in
each node, besides its data, a pointer to each child of
the node.
• However, since the number of children per node can
vary so greatly and is not known in advance, it might
be infeasible to make the children direct links in the
data structure, because there would be too much
wasted space.
• The solution is simple: Keep the children of each
node in a linked list of tree nodes.

13. Implementation of Trees
struct TreeNode
{
char Element;
TreeNode* FirstChild;
TreeNode* NextSibling;
}

14. Implementation of Trees
A
B C GD E F
H I J
K L
A
B C GD E F
H I J
K L
Arrows that point downward are FirstChild pointers.
Arrows that go left to right are NextSibling pointers.
Node E has both a pointer to a sibling (F) and a pointer to a child (I), while some nodes
have neither.

15. Binary trees
• A binary tree is a tree in which no node can
have more than two children.
• Each node has an element, a reference to a
left child and a reference to a right child.
• Maximum number of nodes on level i is 2𝑖−1
for i>=1

16. Full Binary Tree
• A binary tree in which every node has either
two or zero number of children is called Full
Binary Tree

17. Complete Binary Tree
• A binary tree in which all the levels are completely filled
except possibly the last level and the last level has all keys as
left as possible is known as complete binary tree.
• In a Binary tree all internal nodes have 2 children and all
leaves are at same level then it is called perfect binary tree.
• Maximum Number of nodes = 2d+1 – 1
• Number of leaf nodes = 2d , Where, d – Depth of the tree

18. Left Skewed and Right Skewed Trees
• Binary tree has only left sub trees - Left
Skewed Trees
• Binary tree has only right sub trees - Right
Skewed Trees

19. Binary Tree Representation
1. Sequential representation using arrays
2. List representation using Linked list

20. Sequential representation
• To represent a binary tree of depth ‘d' using array
representation, we need one dimensional array with a
maximum size of 2d+1 - 1.

21. Sequential Representation
For any element in array position i, its left and
right child are in the position given by
• Left child= 2*i
• Right child= 2*i+1
• Parent= i/2

22. Sequential representation
• Advantages:
– Direct access to all nodes (Random access)
• Disadvantages:
– Height of tree should be known
– Memory may be wasted
– Insertion and deletion of a node is difficult

23. List representation
struct node
{
int data;
struct node *left;
struct node *right;
};

24. List Representation
• Each node is a structure consisting of the
element and pointer to the left and right child
of a node
• For every binary tree with N nodes would
require N+1 NULL pointers.

25. List representation
• Advantages:
– Height of tree need not be known.
– No memory wastage.
– Insertion and deletion of a node is done without
affecting other nodes.
• Disadvantages:
– Direct access to node is difficult.
– Additional memory required for storing address of
left and right node.

26. Applications of trees
• Trees are used to store simple as well as
complex data.
• Trees are often used for implementing other
types of data structures like hash tables, sets
and maps.
• Trees are used in database design, file system
directories.
• Trees are also widely used for information
storage and retrieval in symbol tables.

27. Class Poll
1. Node with out degree zero is called
A. Root
B. Sub tree
C. Leaf
D.Internal Nodes

28. Class Poll
2. In tree Construction which is suitable and
efficient data structure?
A.Array
B. Linked List
C. Stack
D.Queue

29. Class Poll
3. Using the array implementation of tree, the
right child of the key value in index i is found at
what index?
a) i + 2
b) 2i
c) 2i + 1
d) 2i + 2