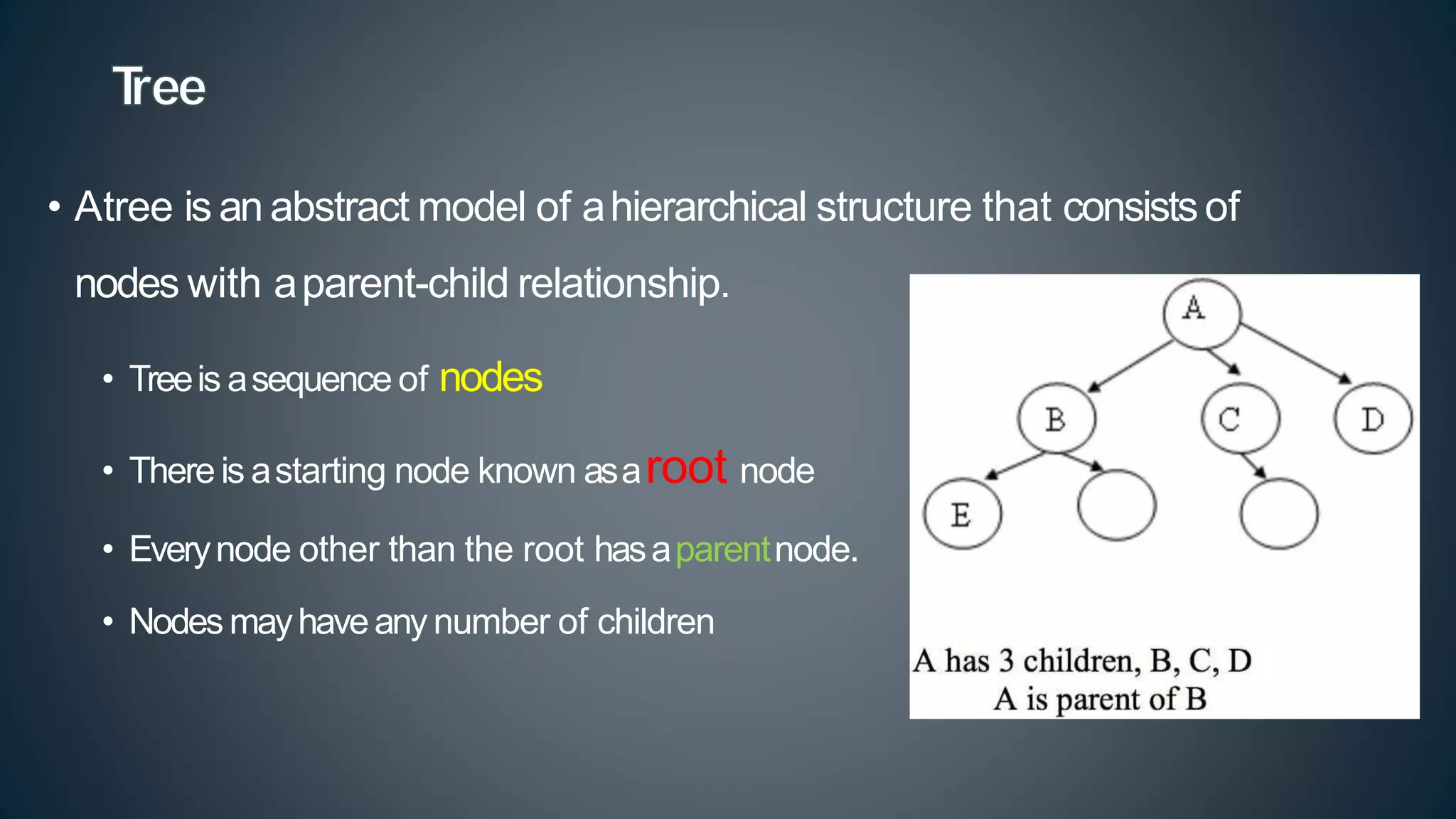
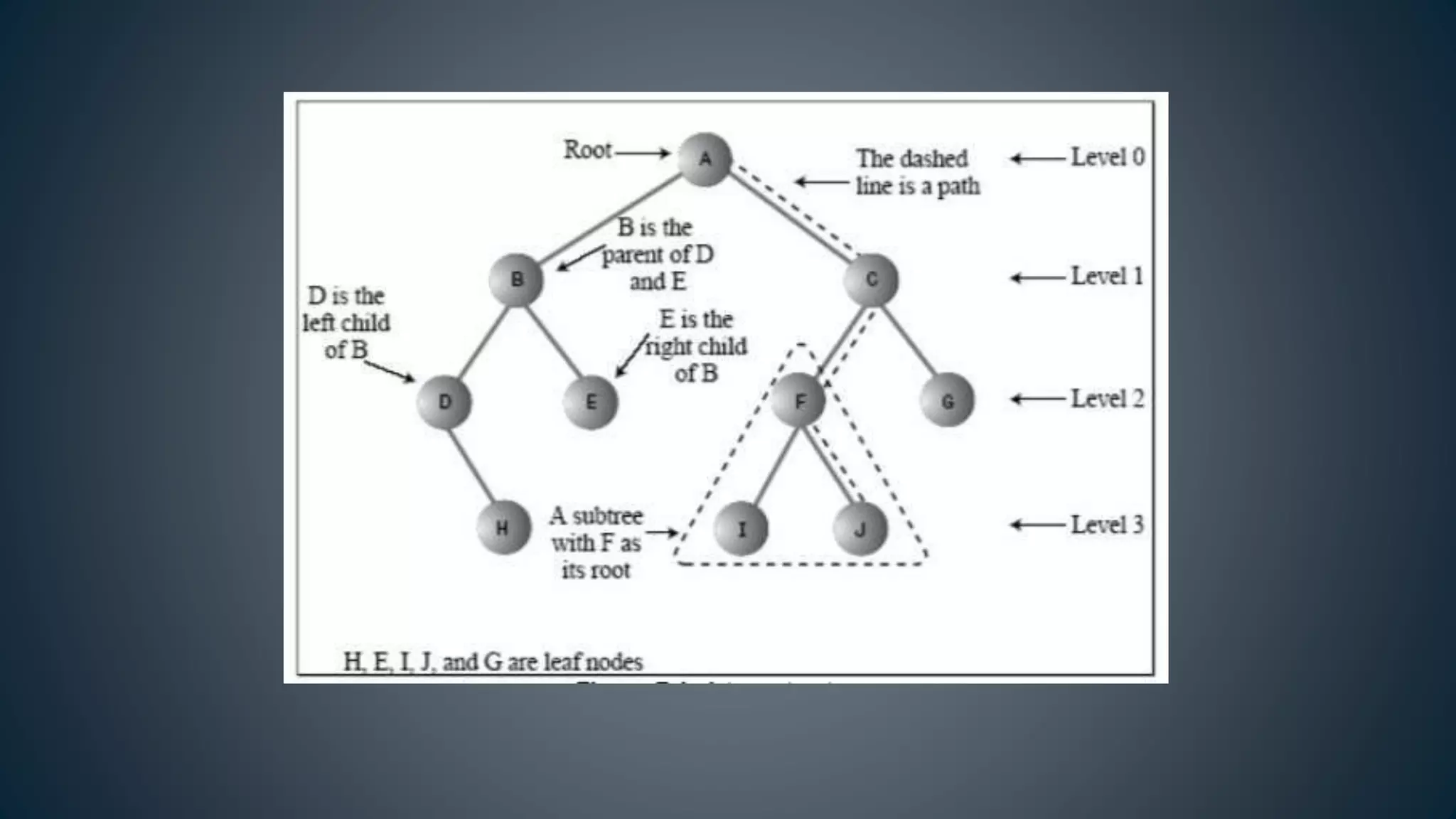
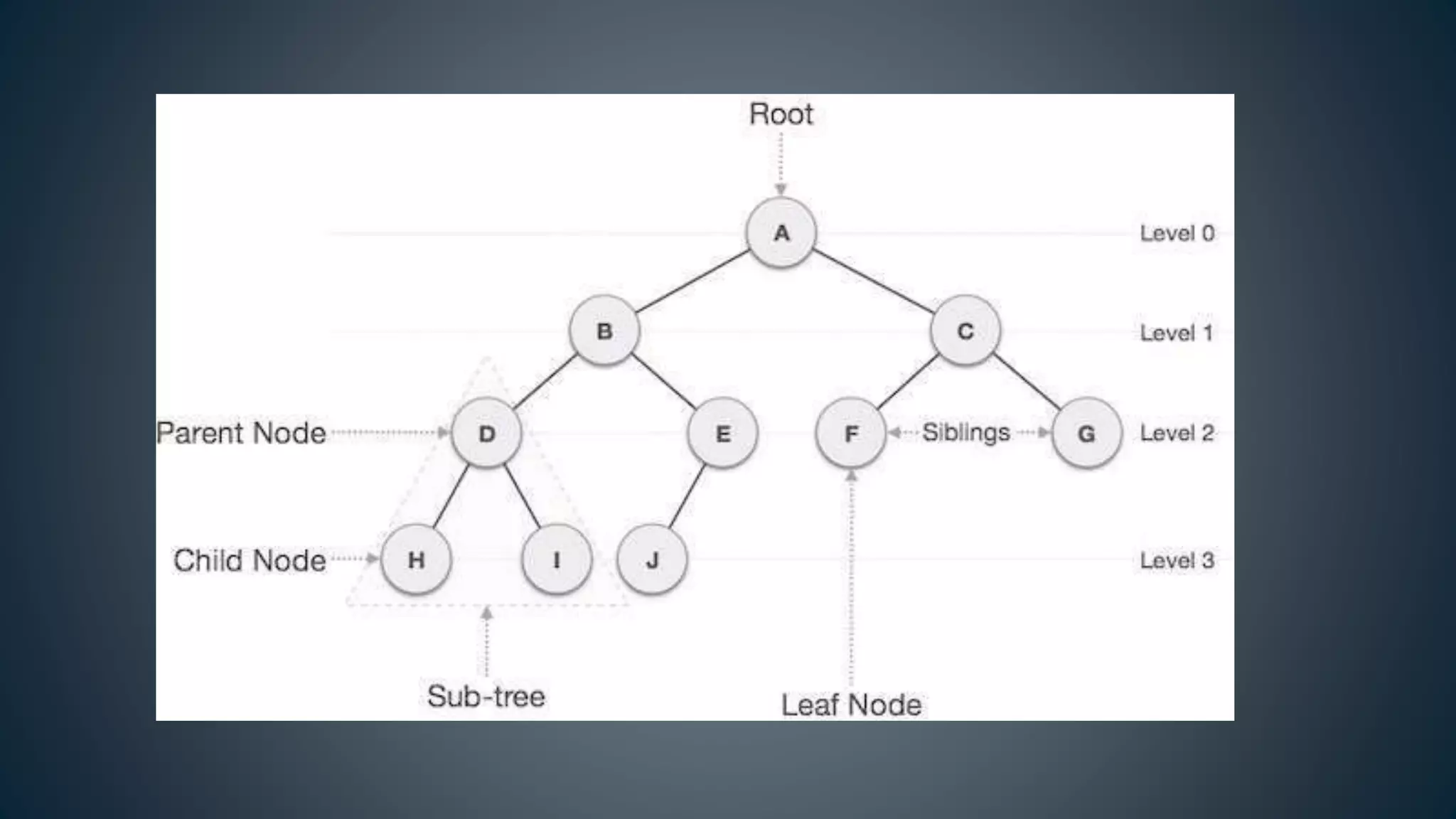
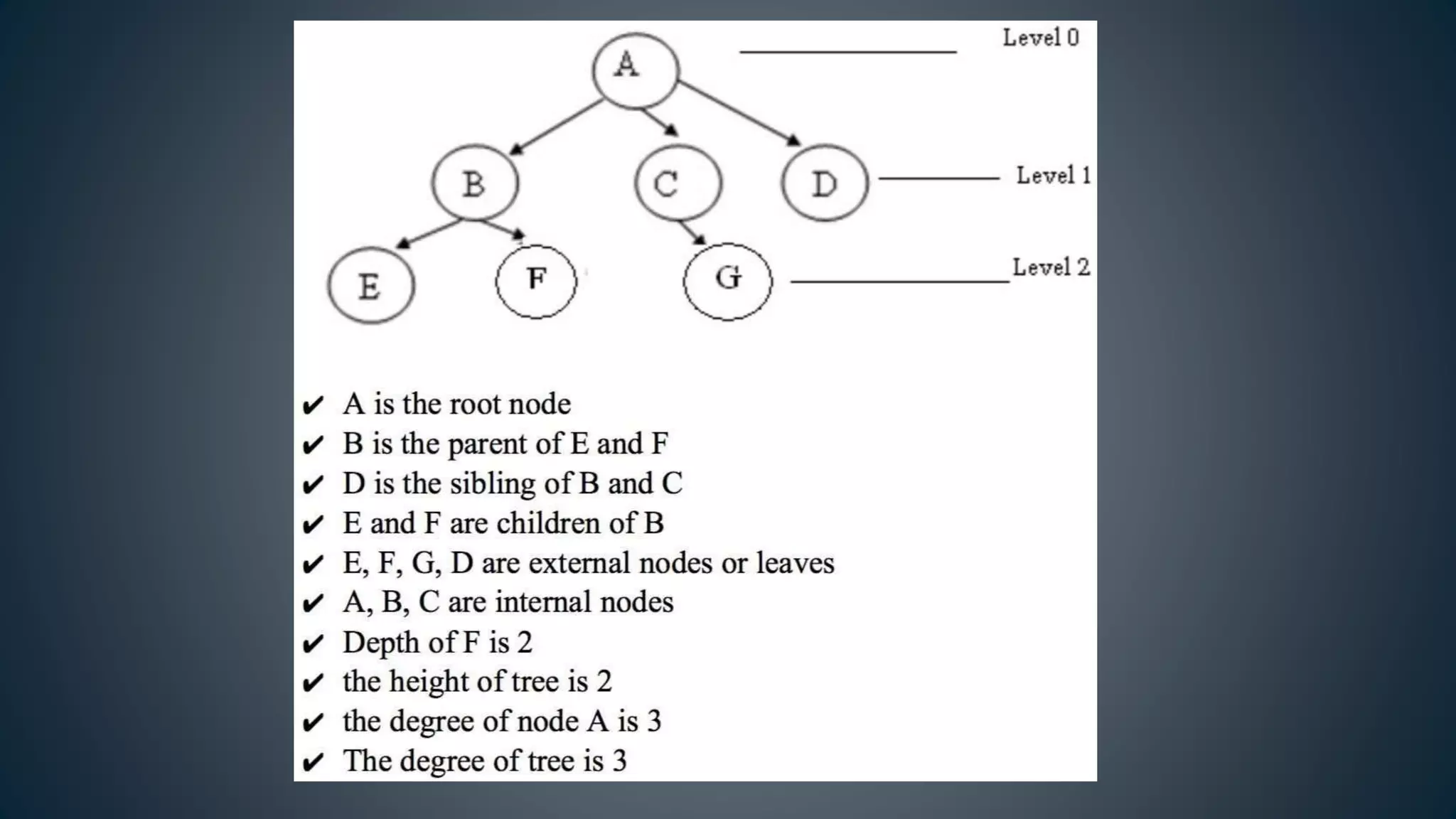
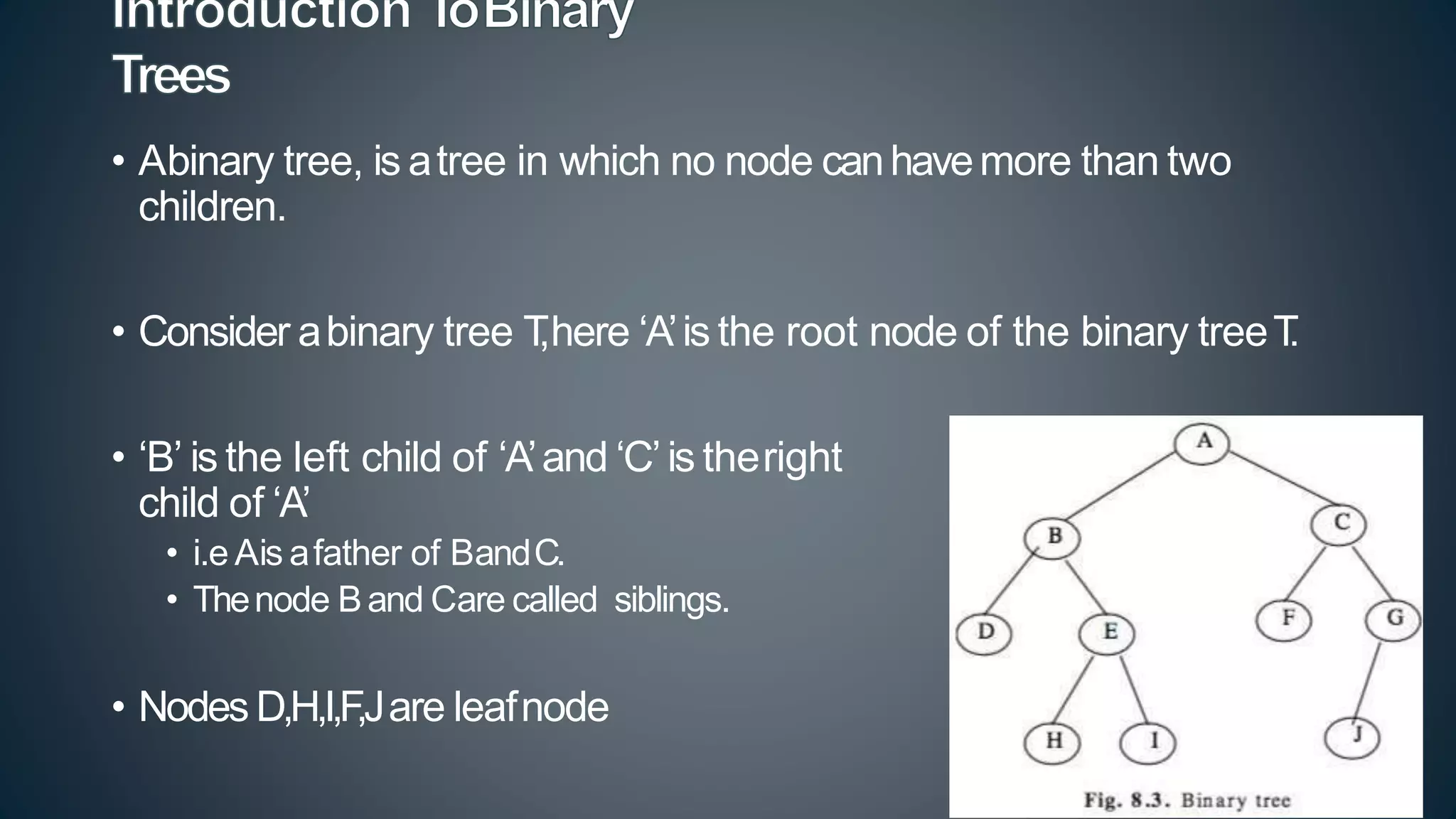
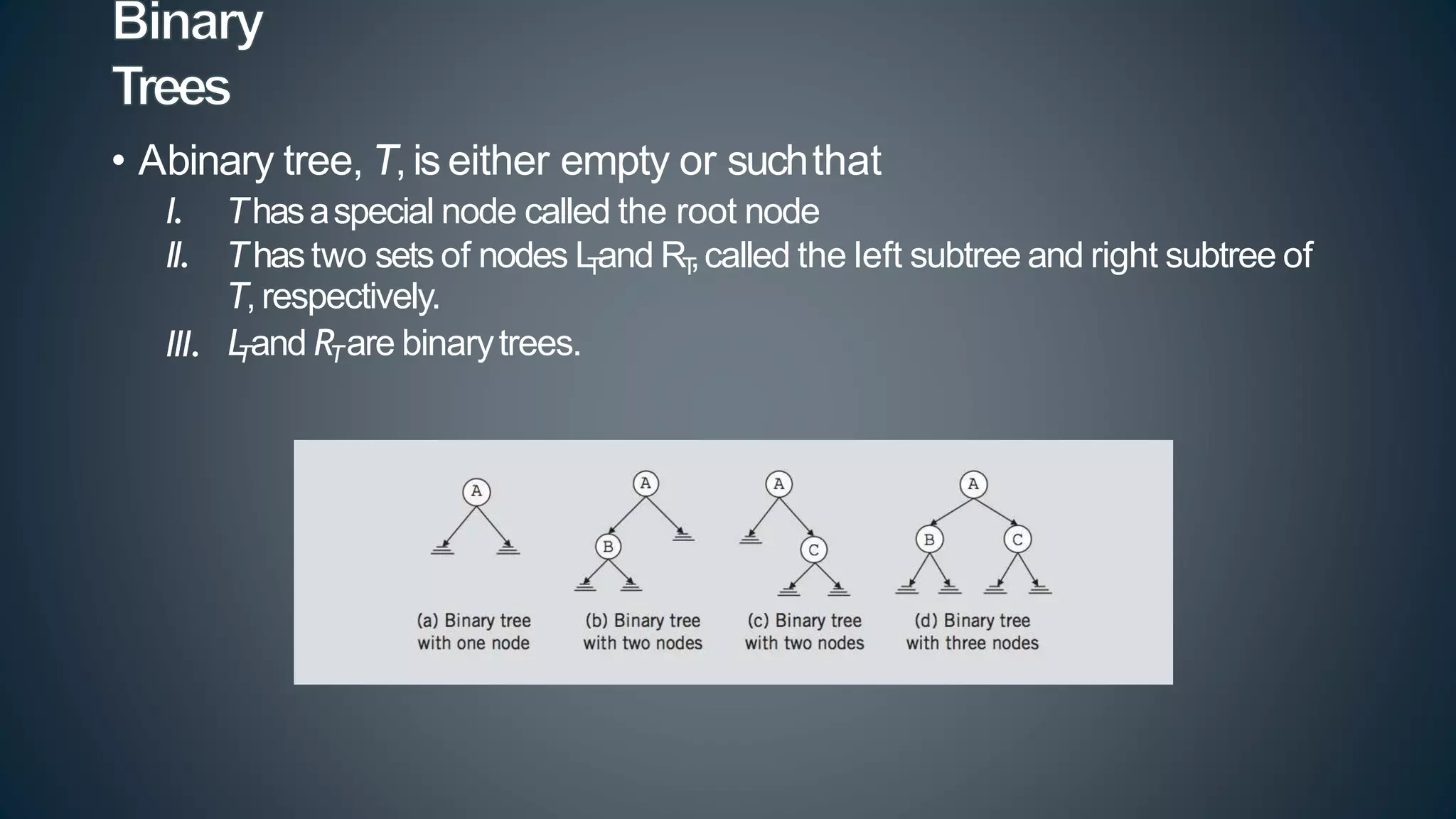
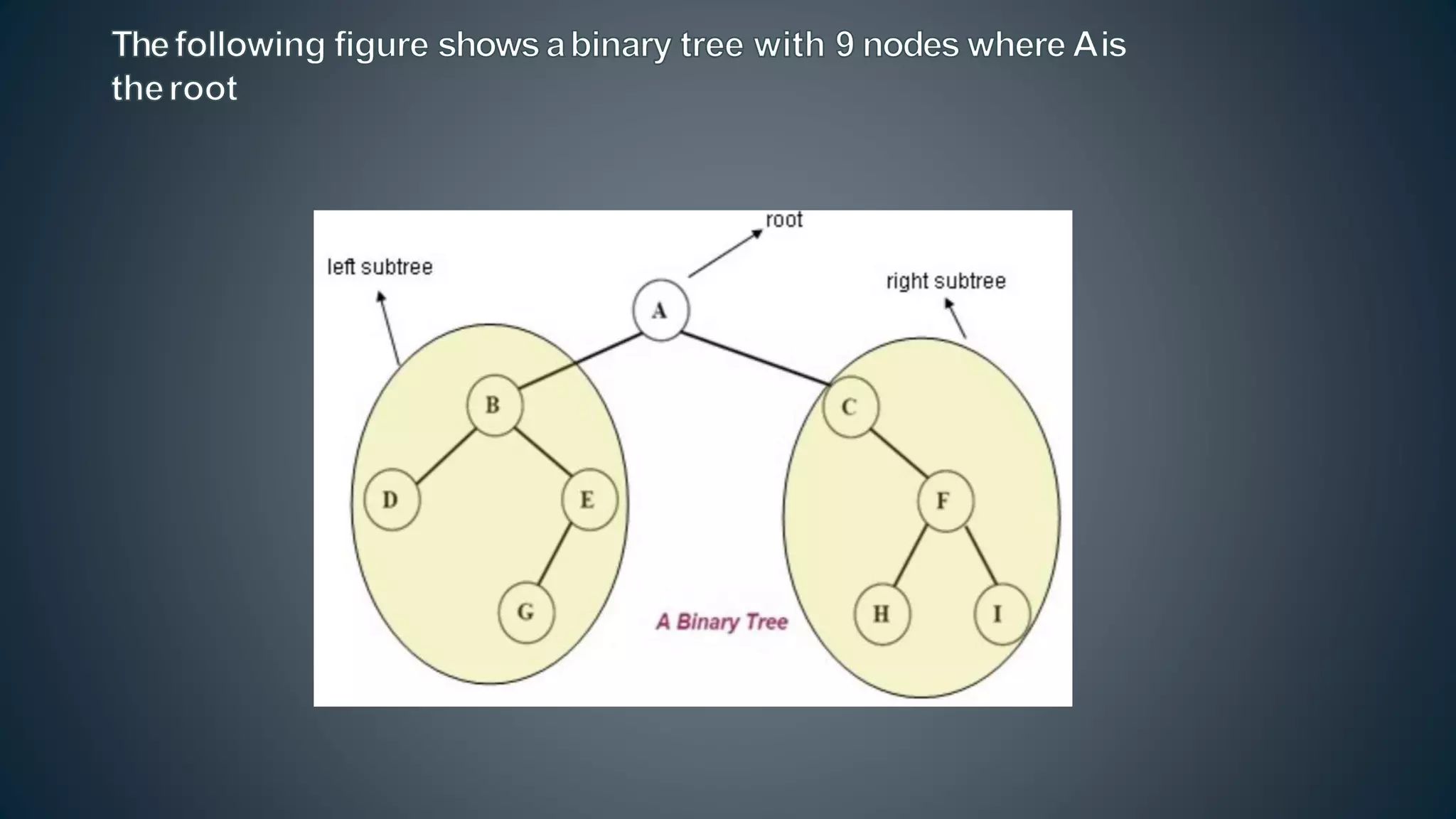
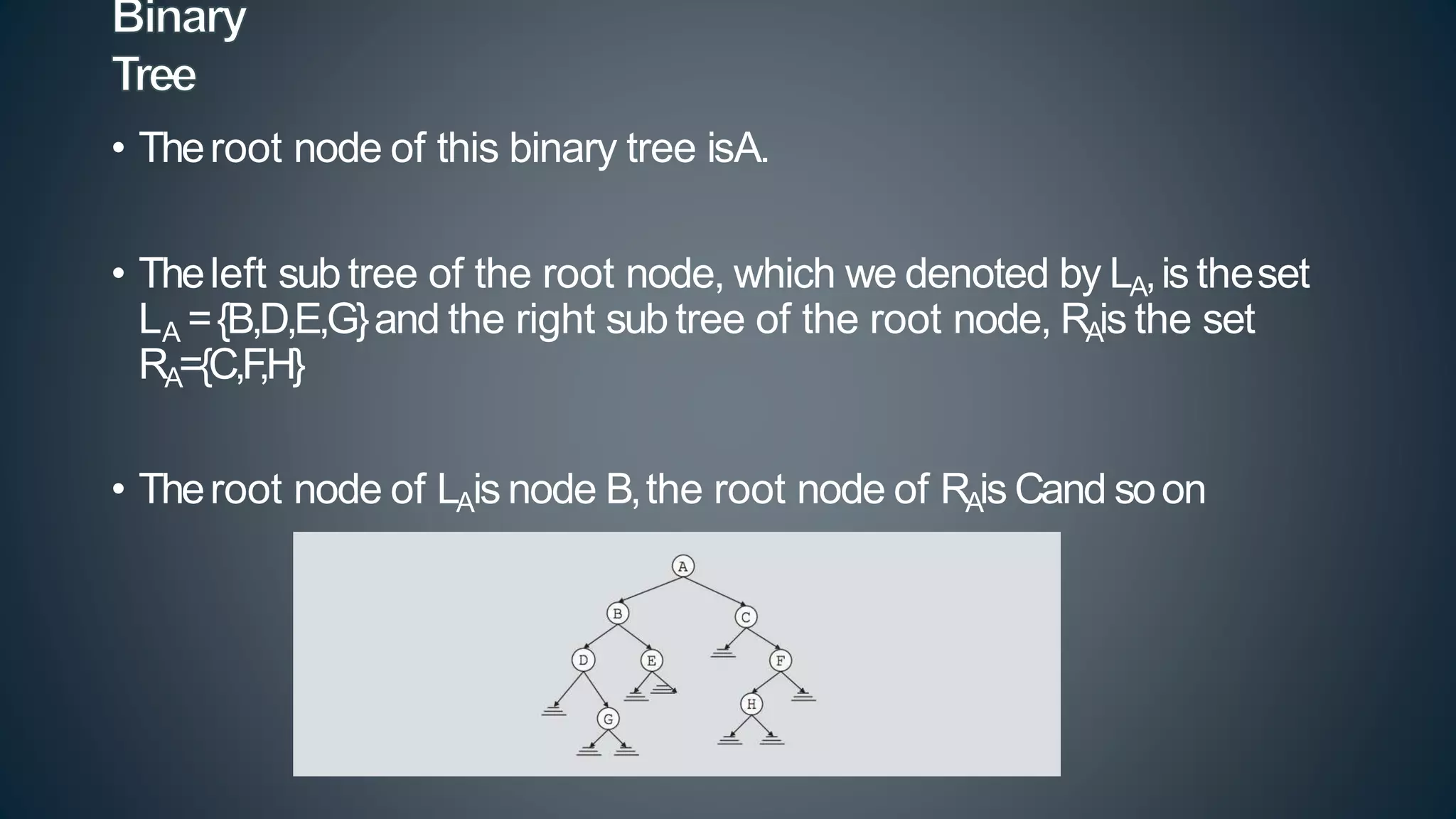
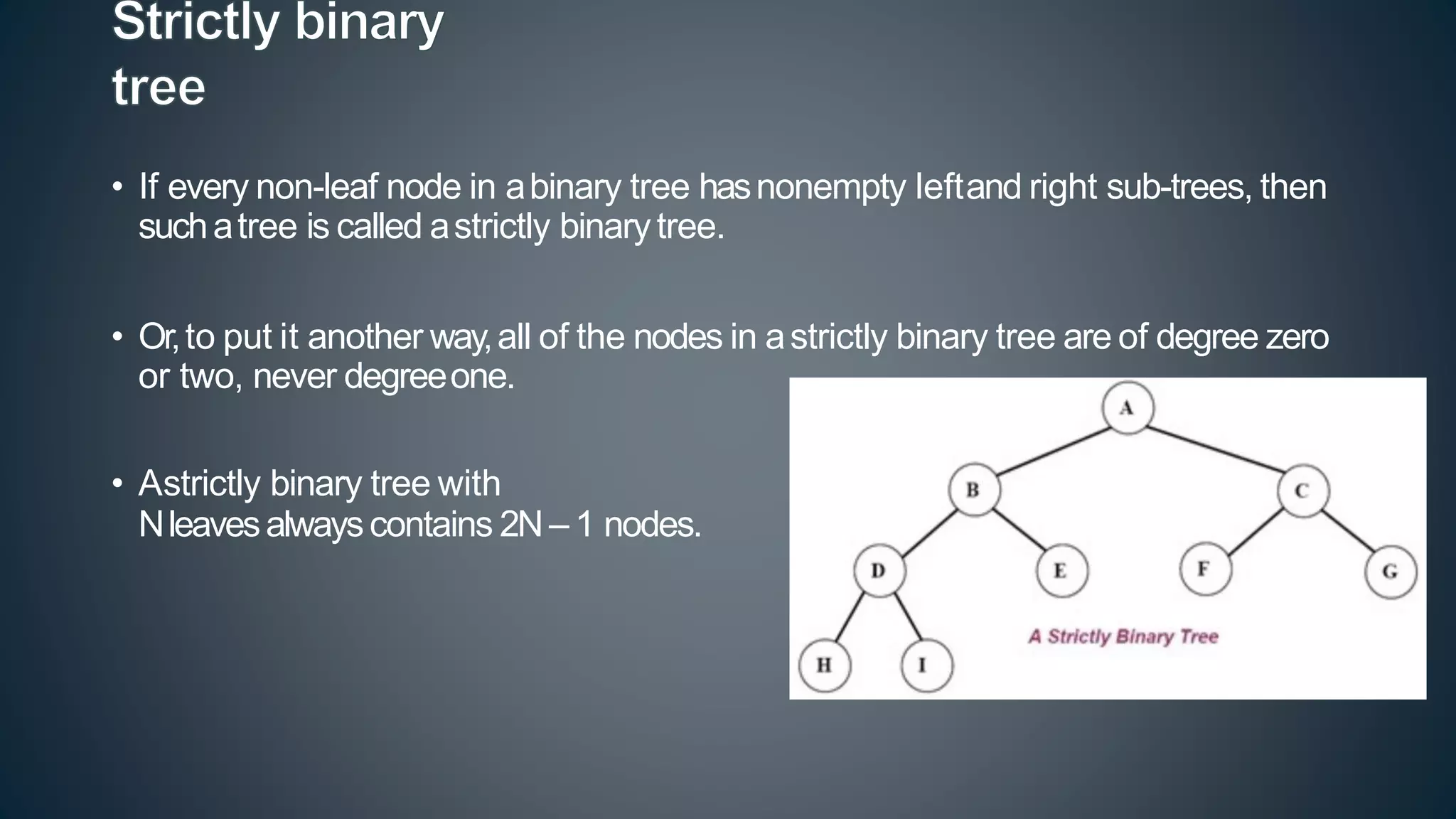
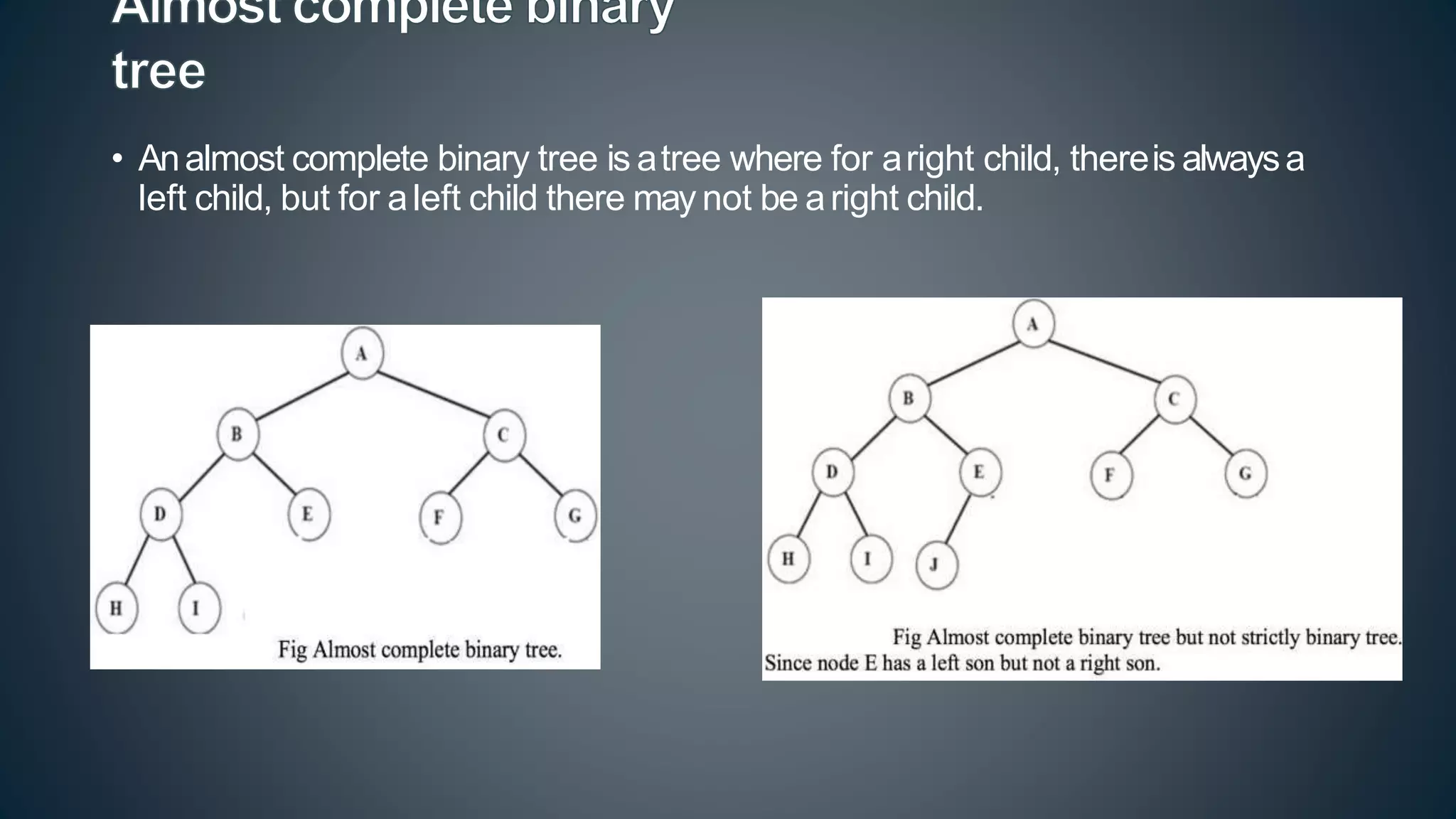
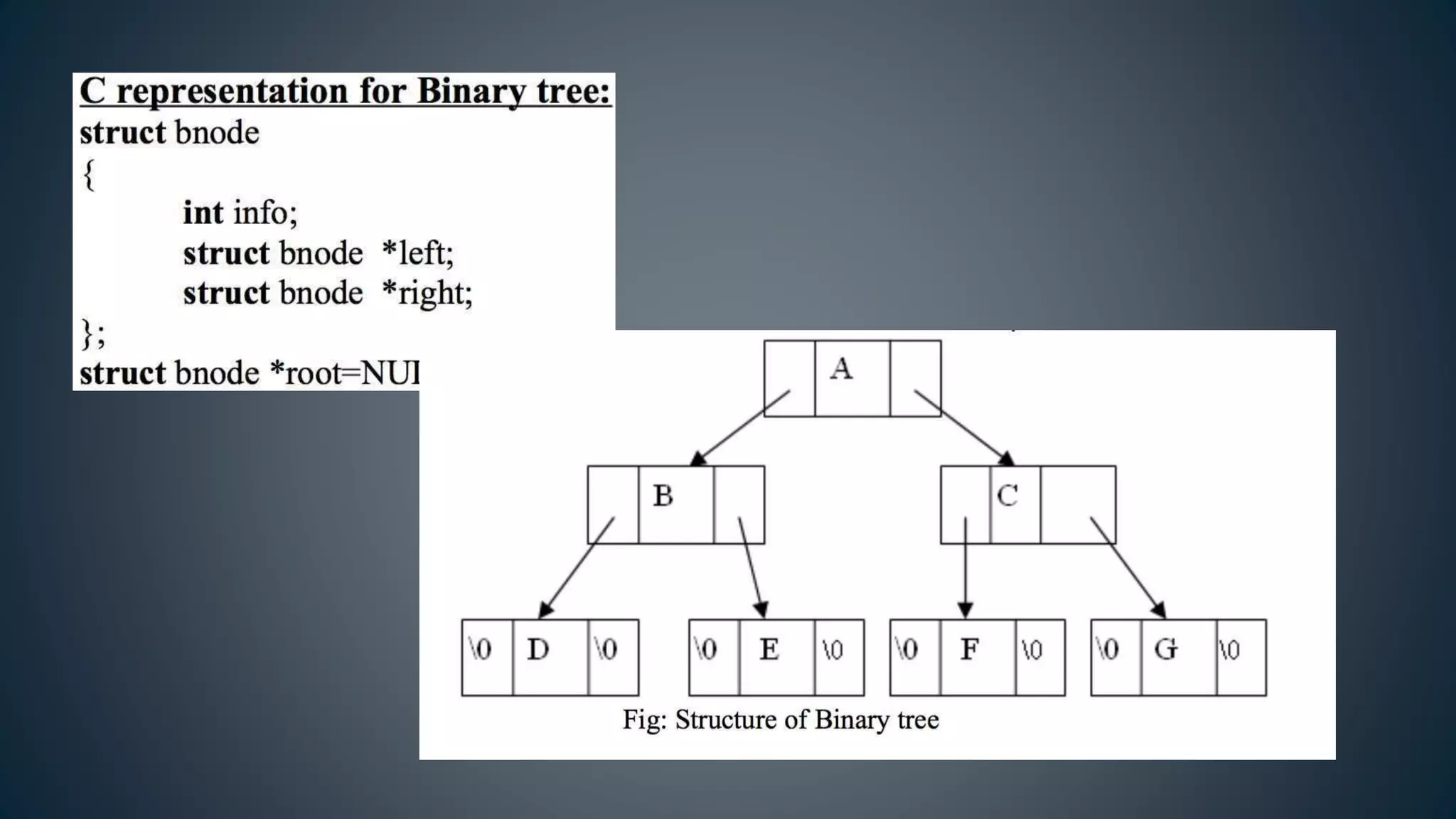
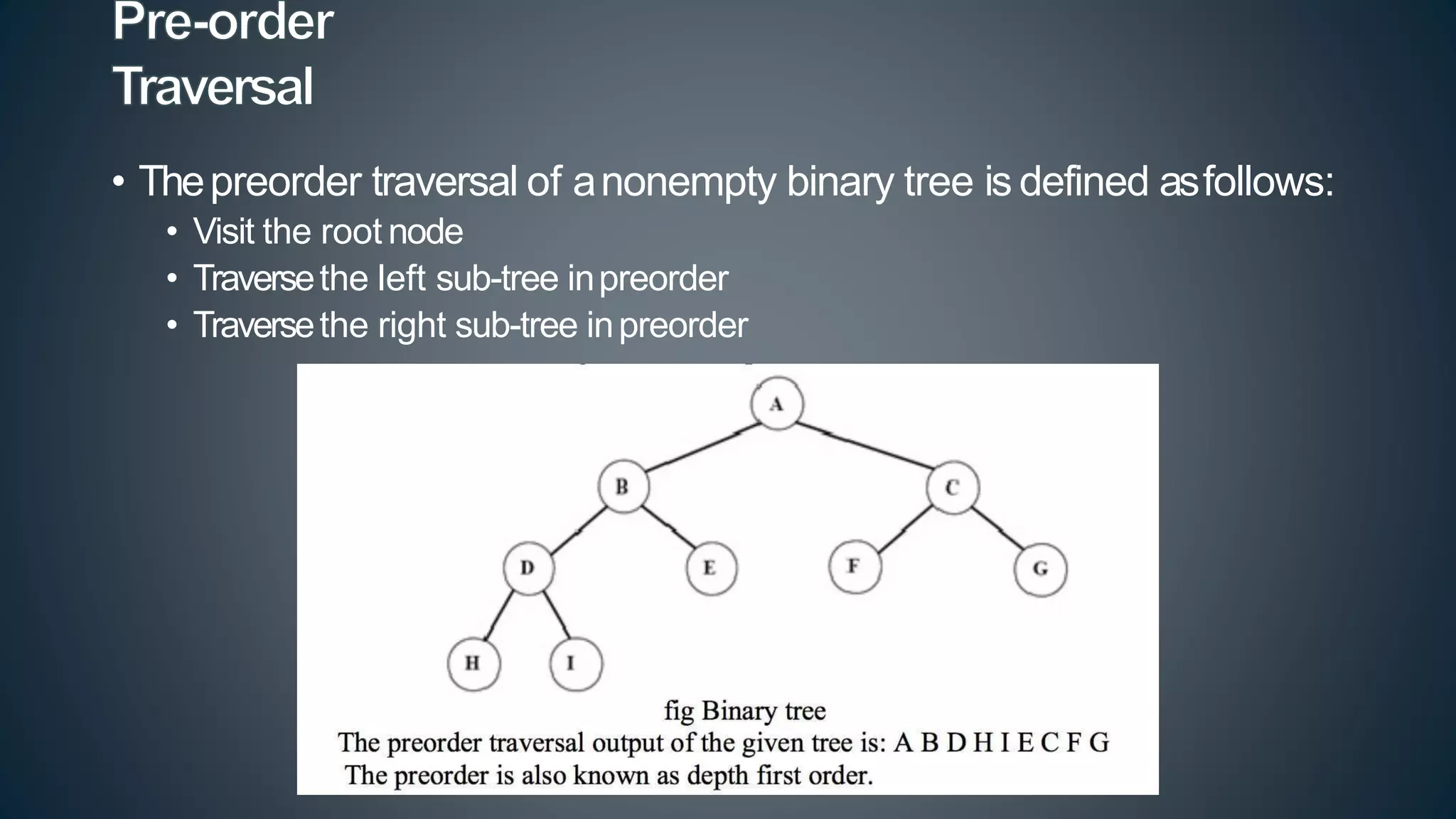
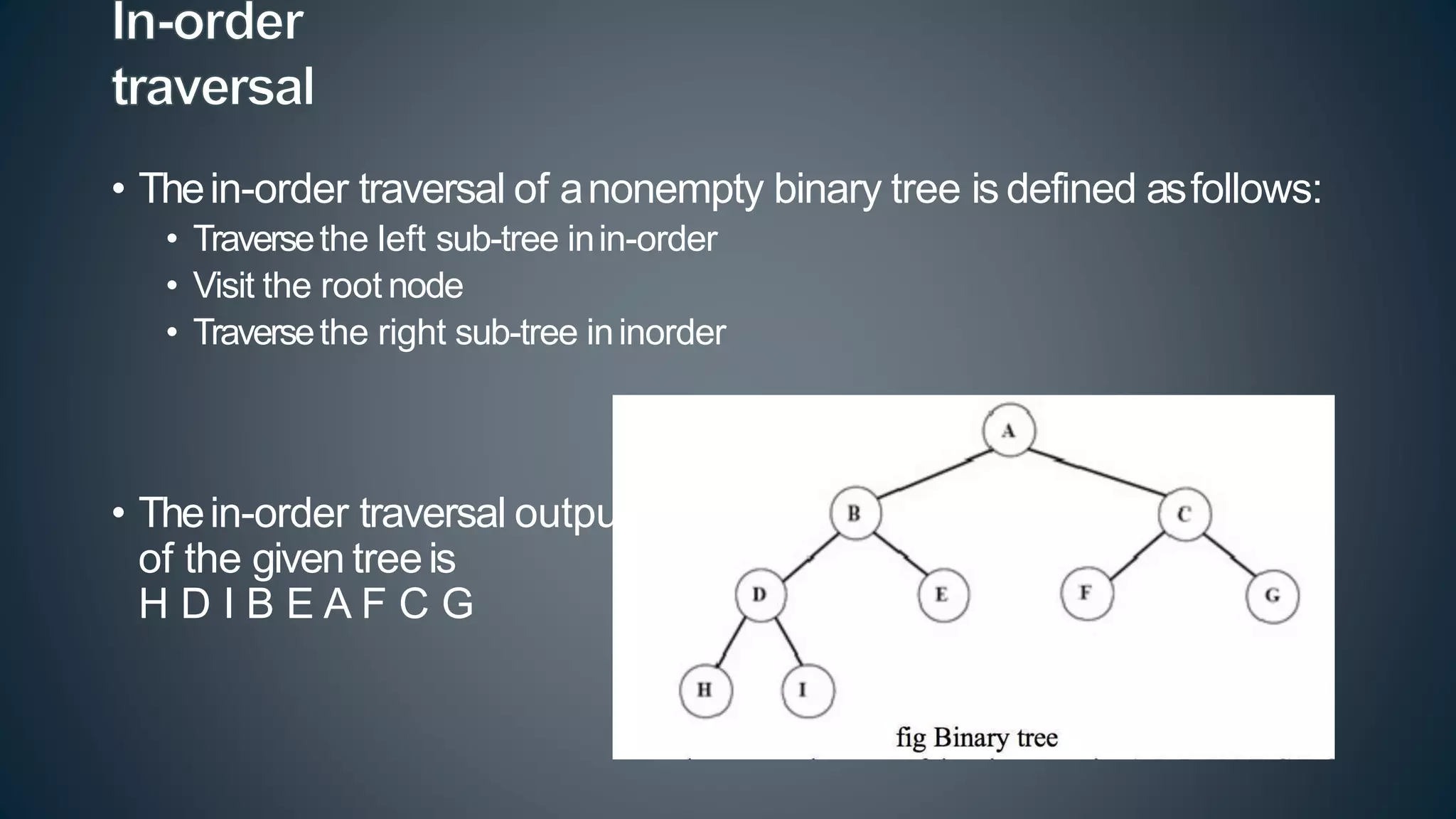
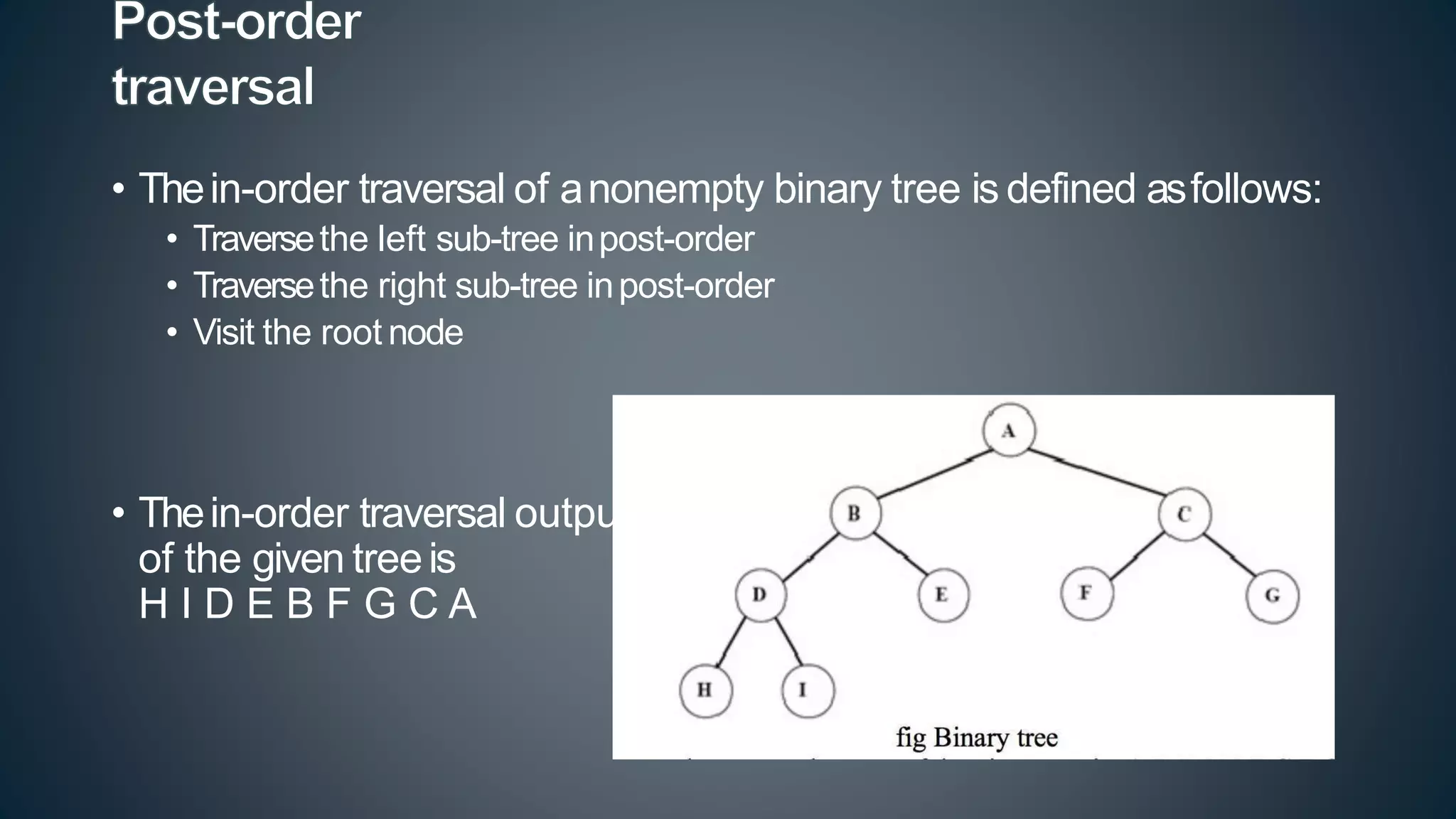
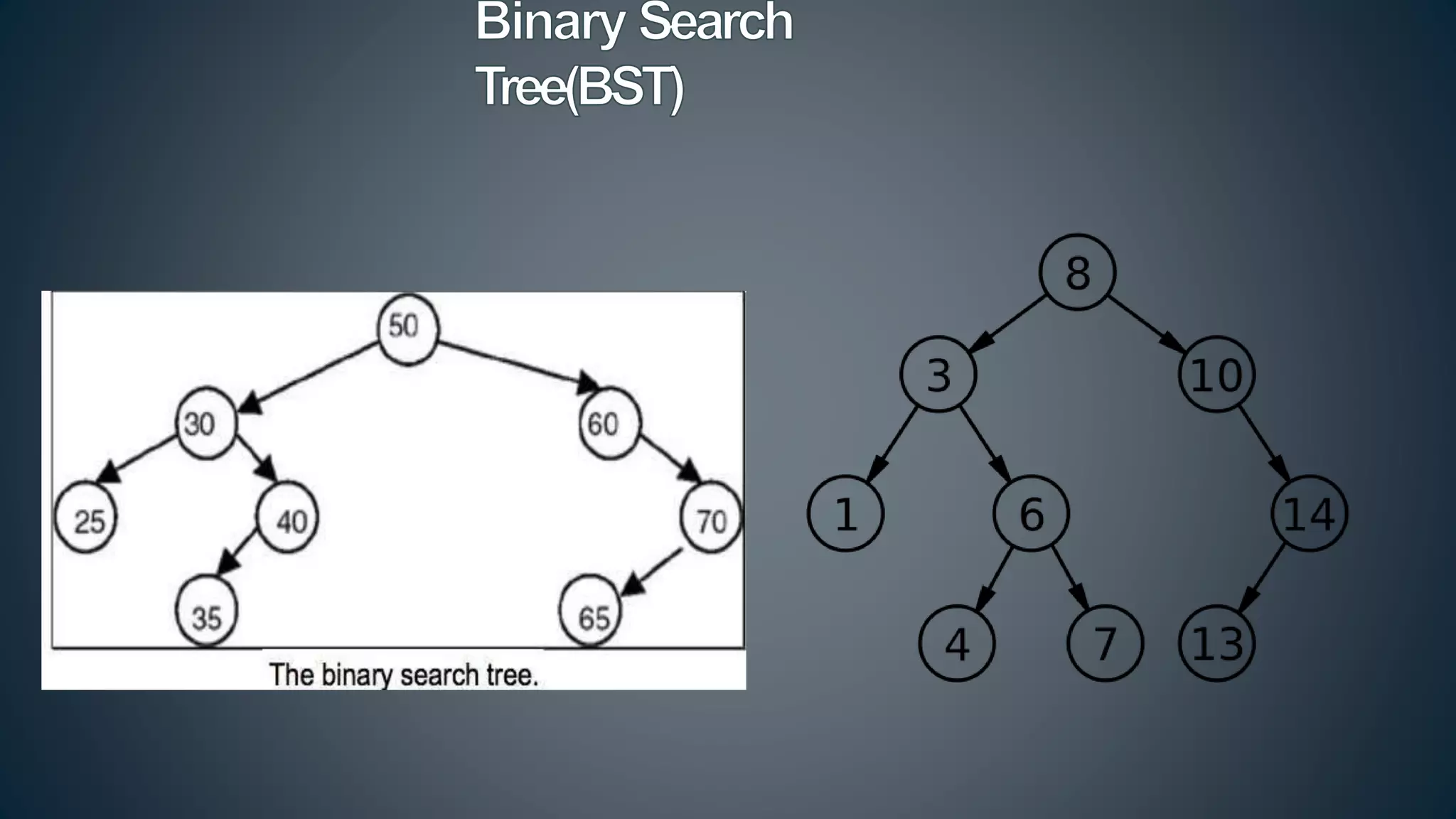
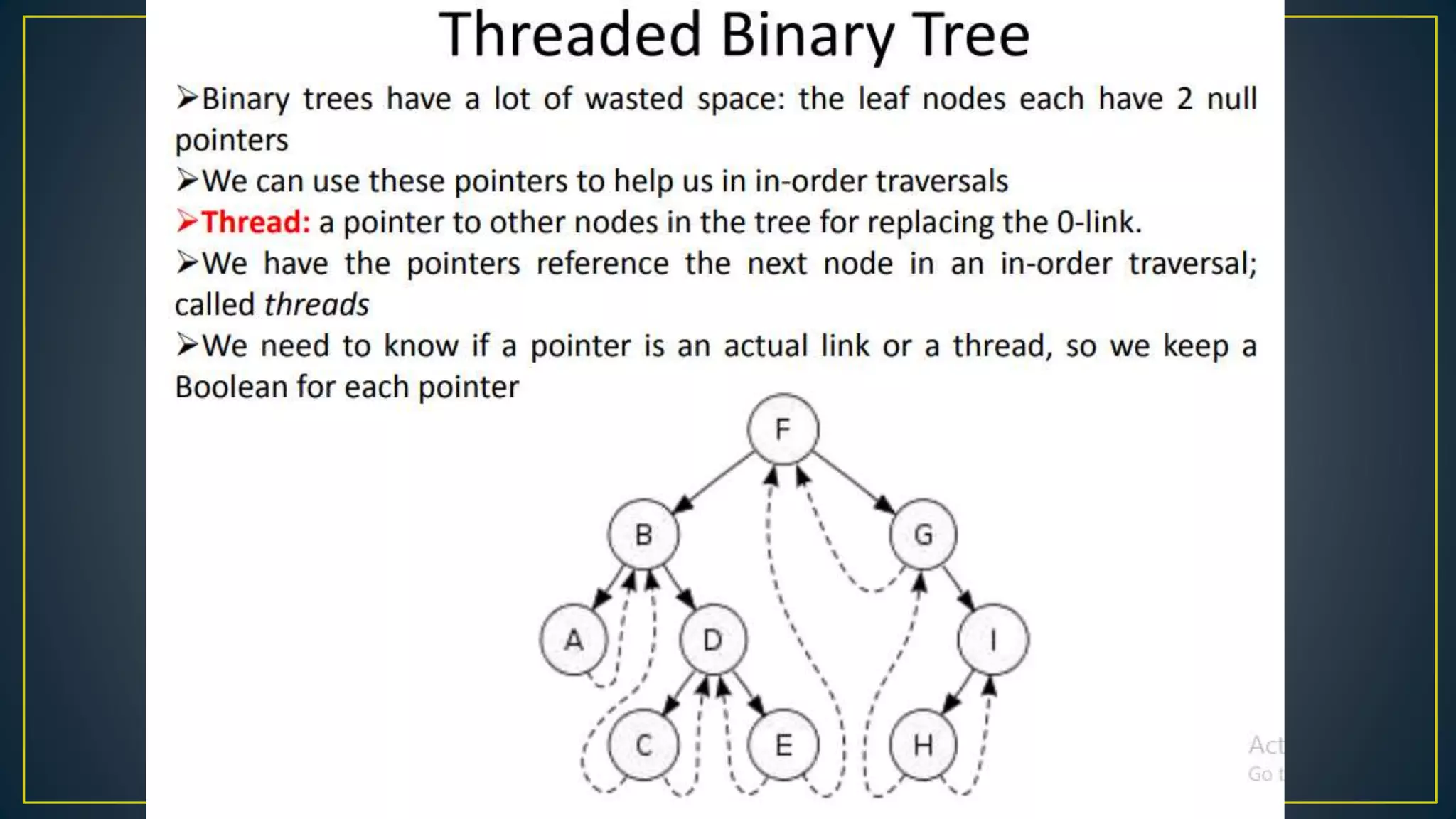
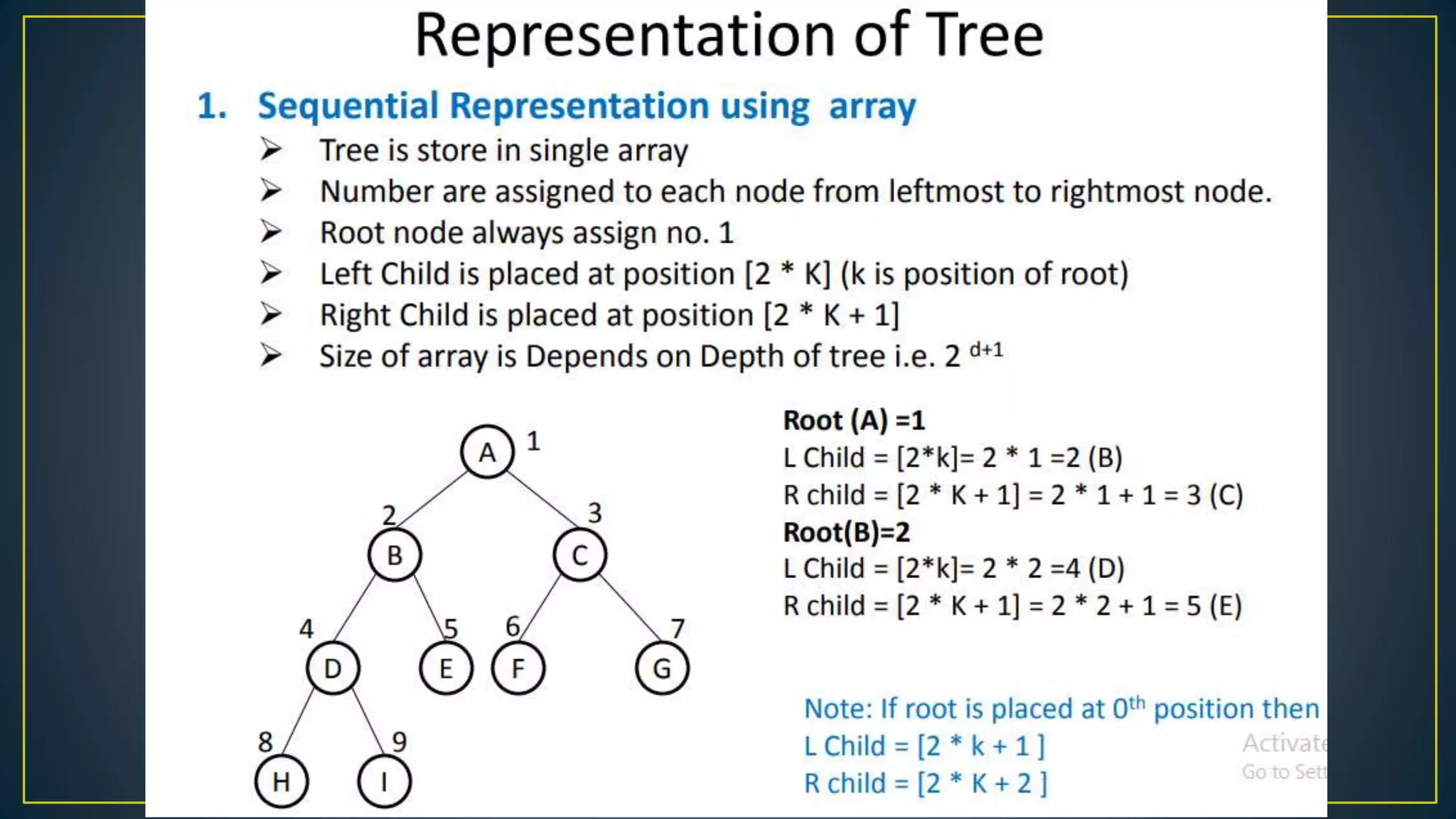
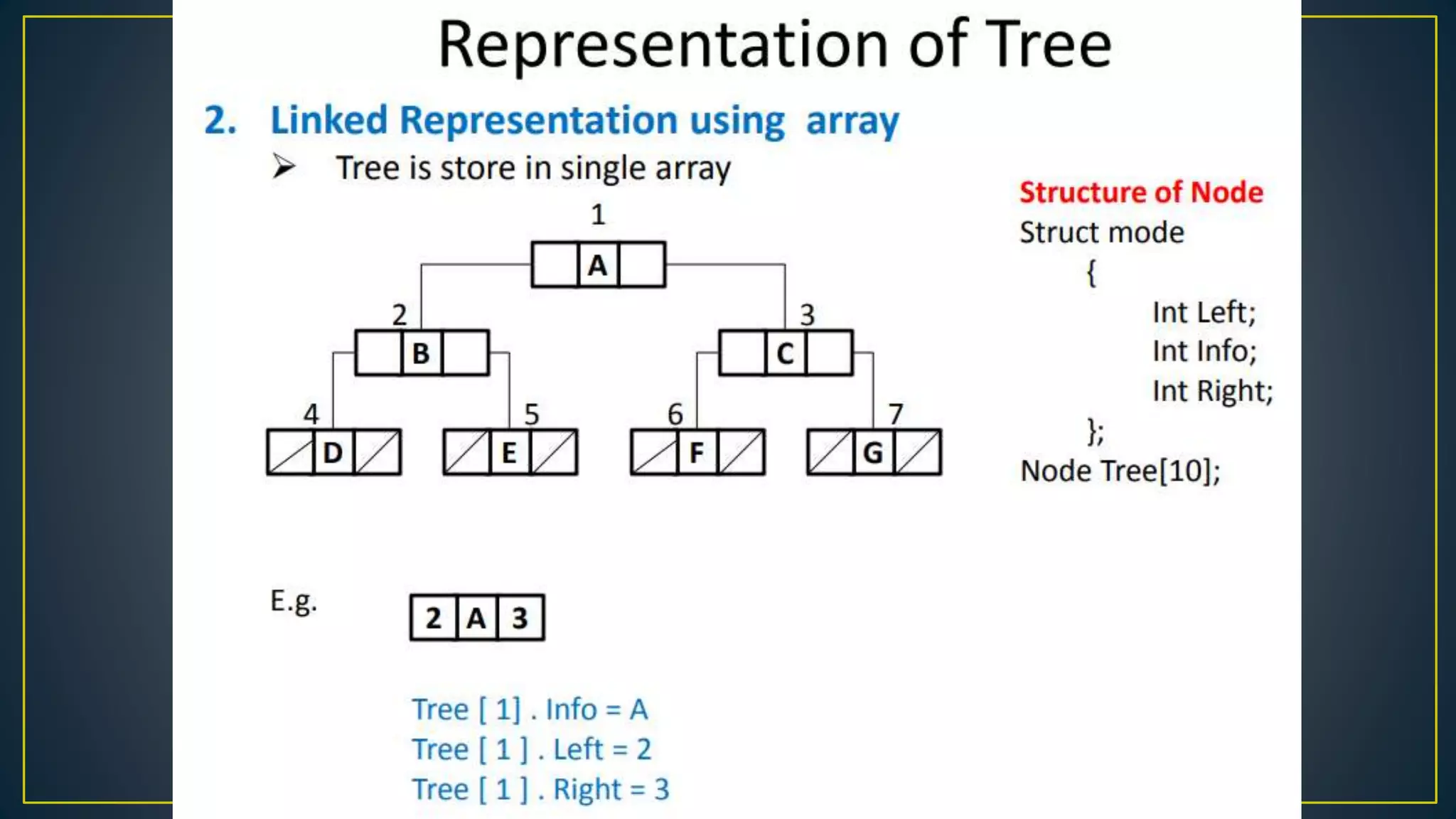
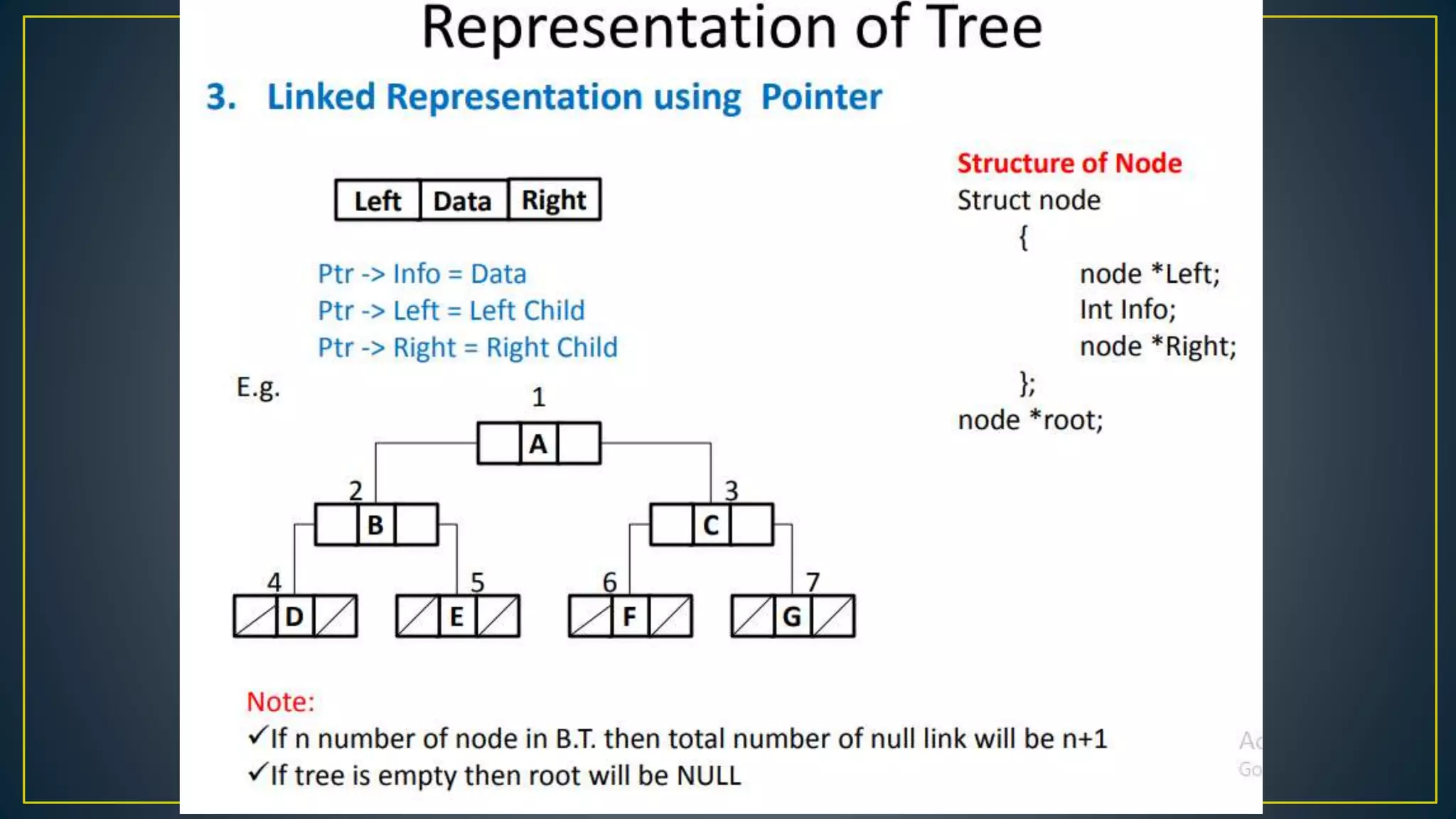
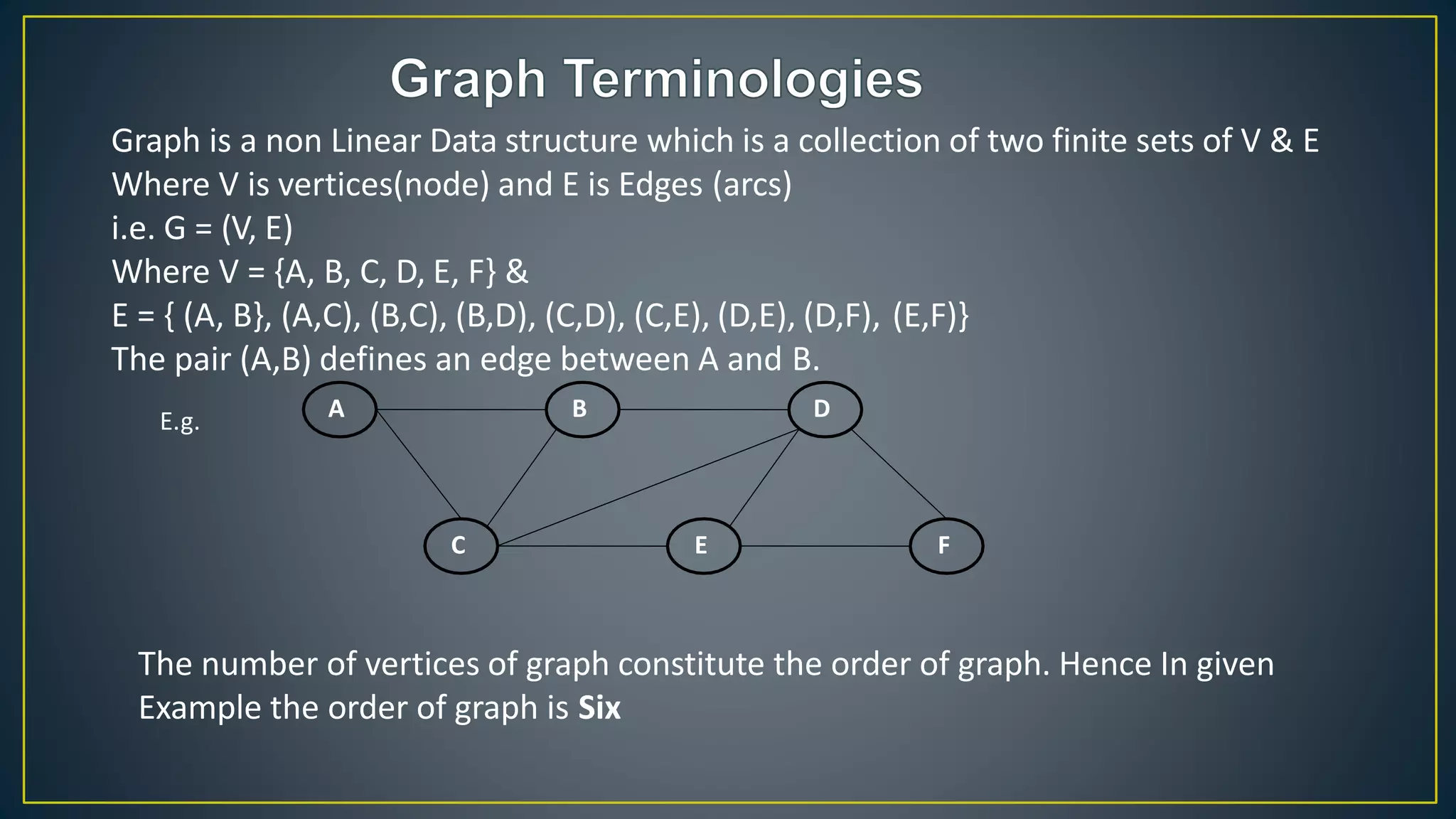
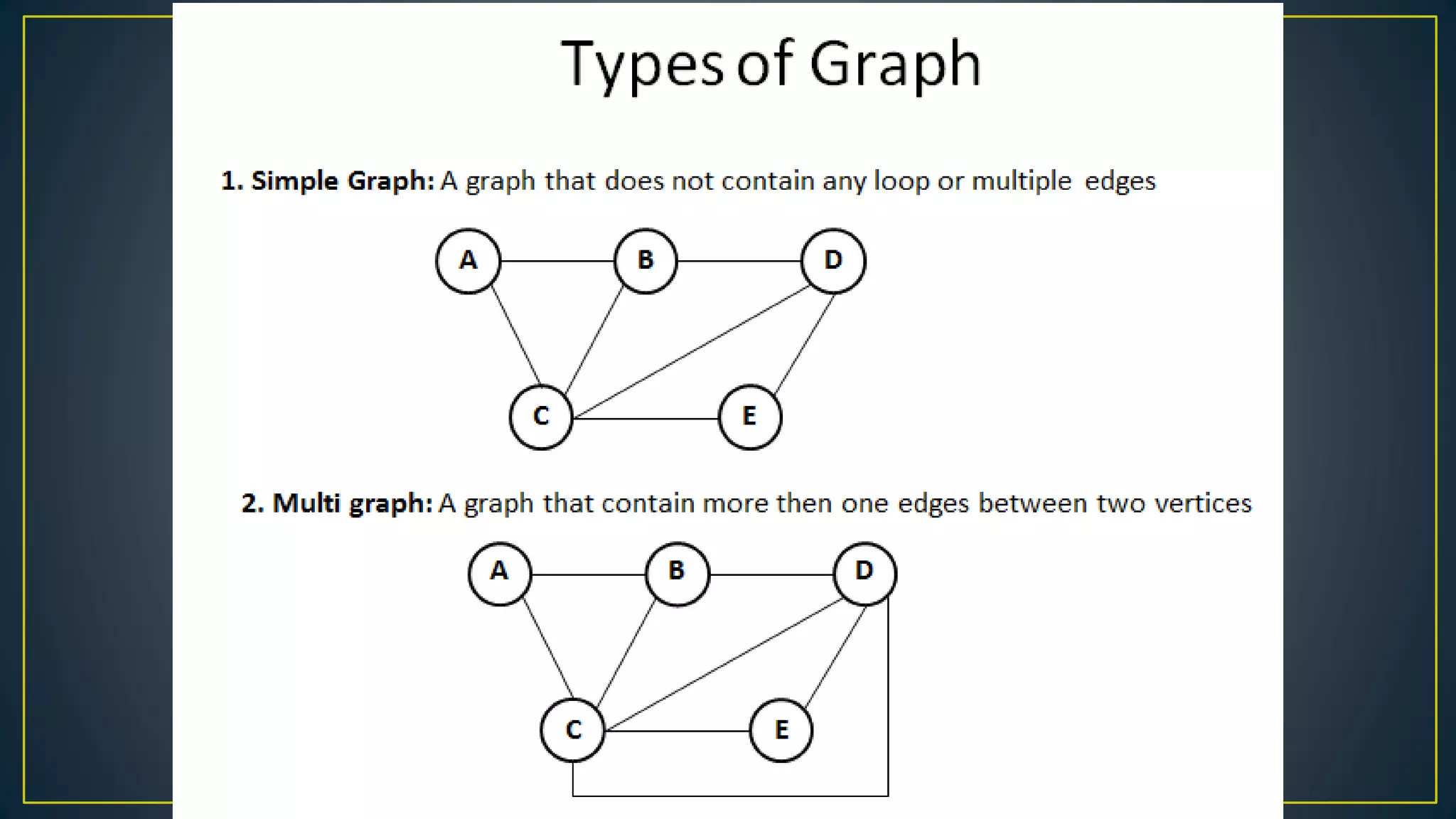
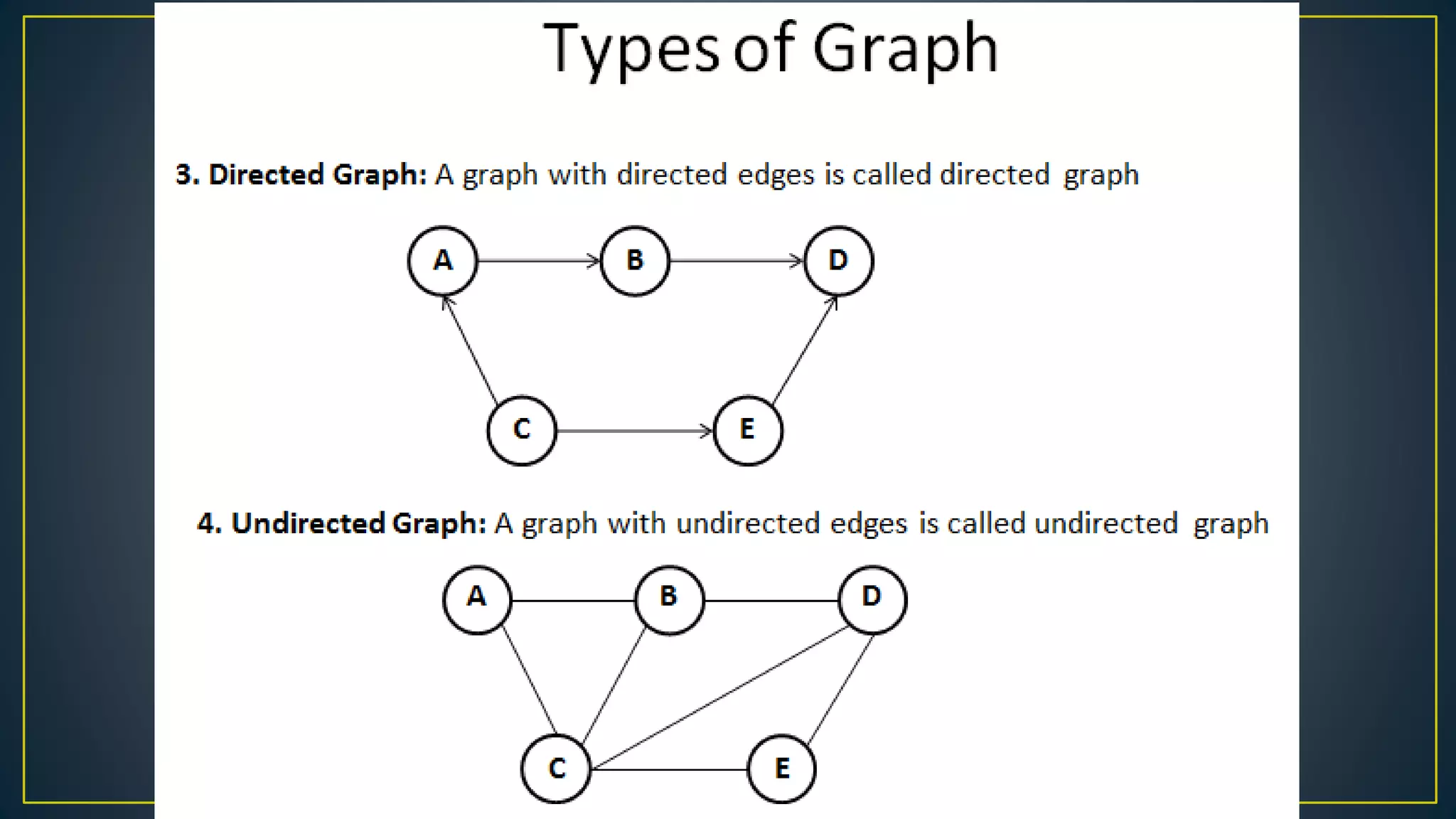
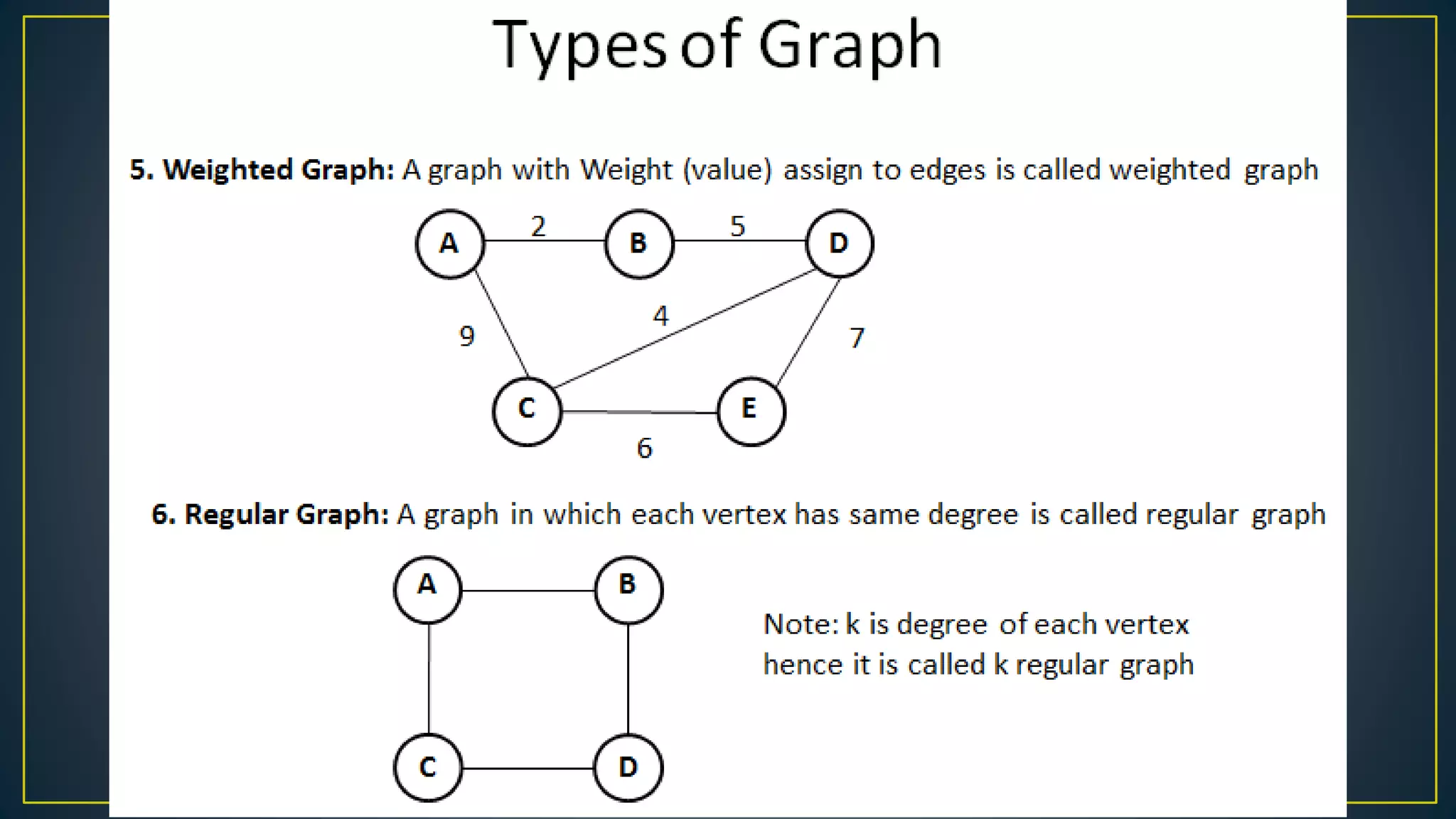
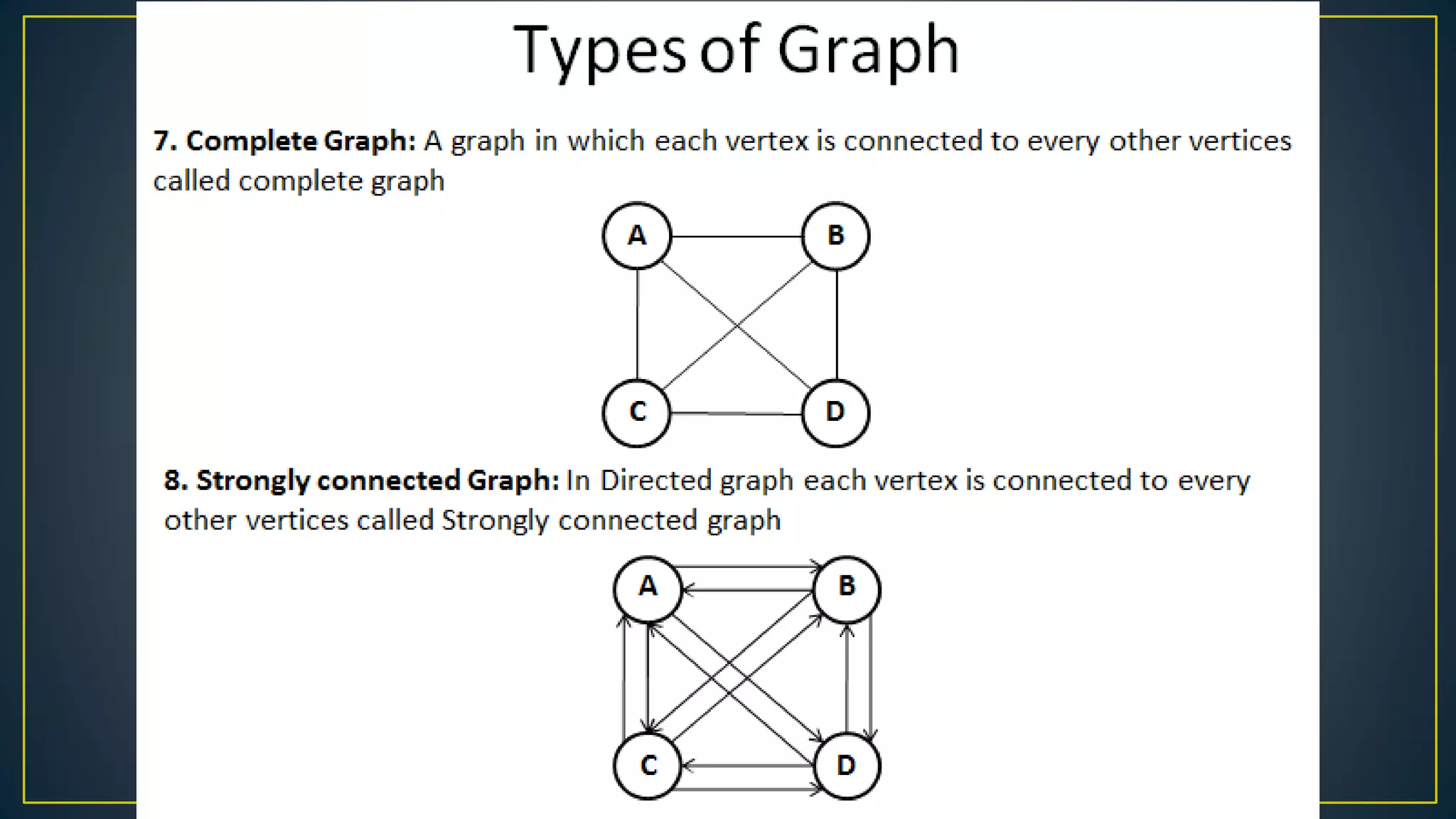
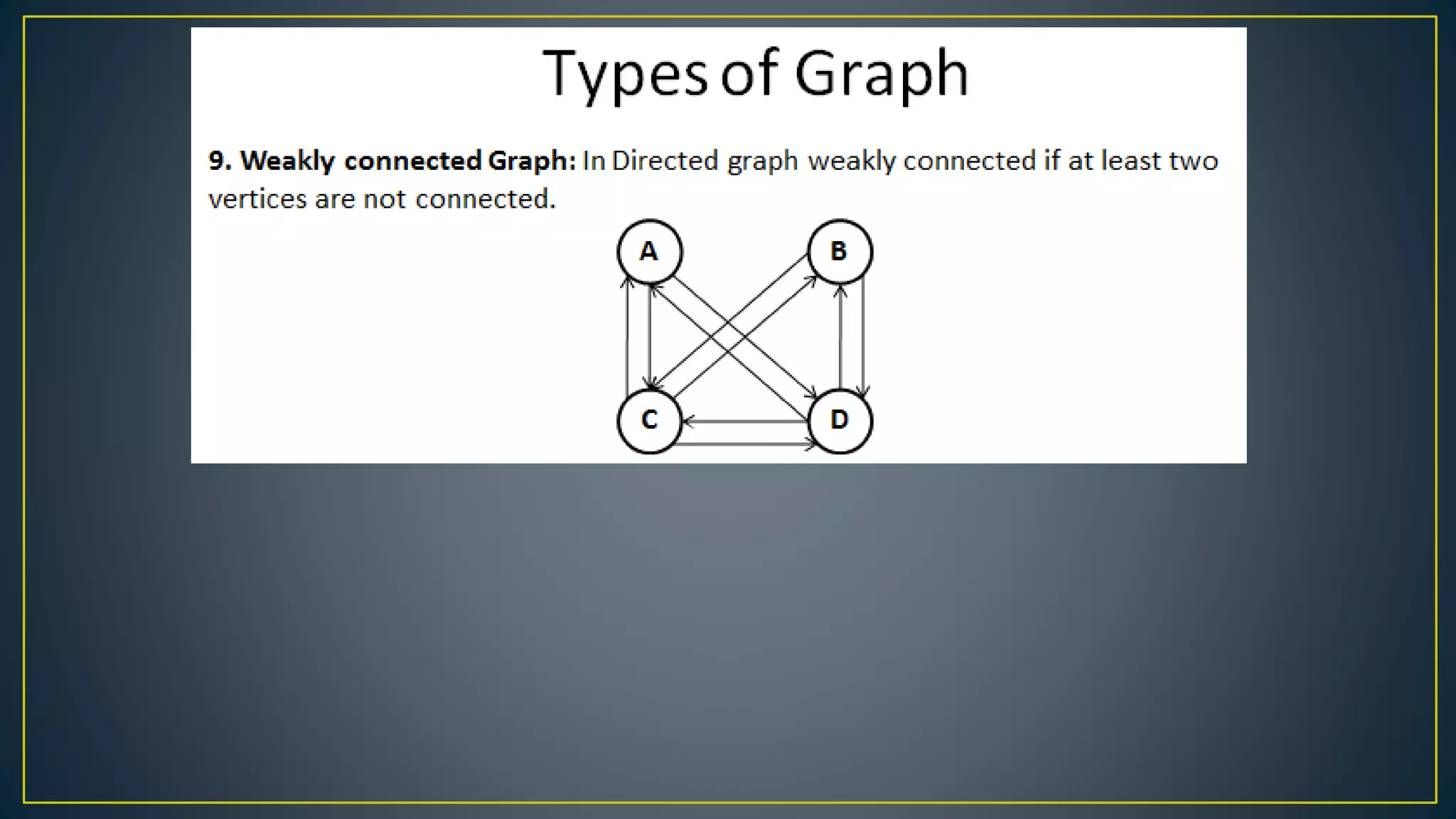
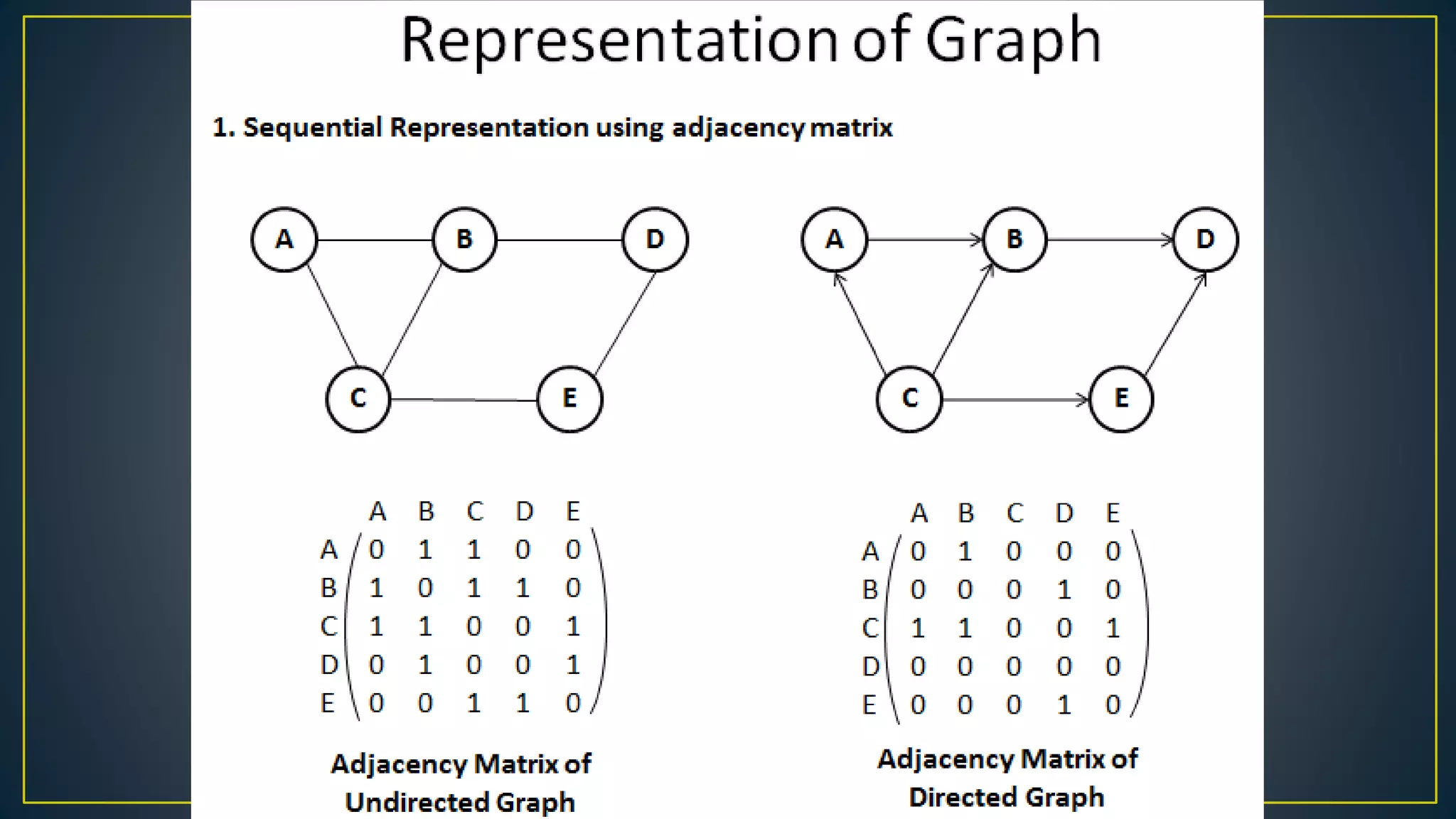
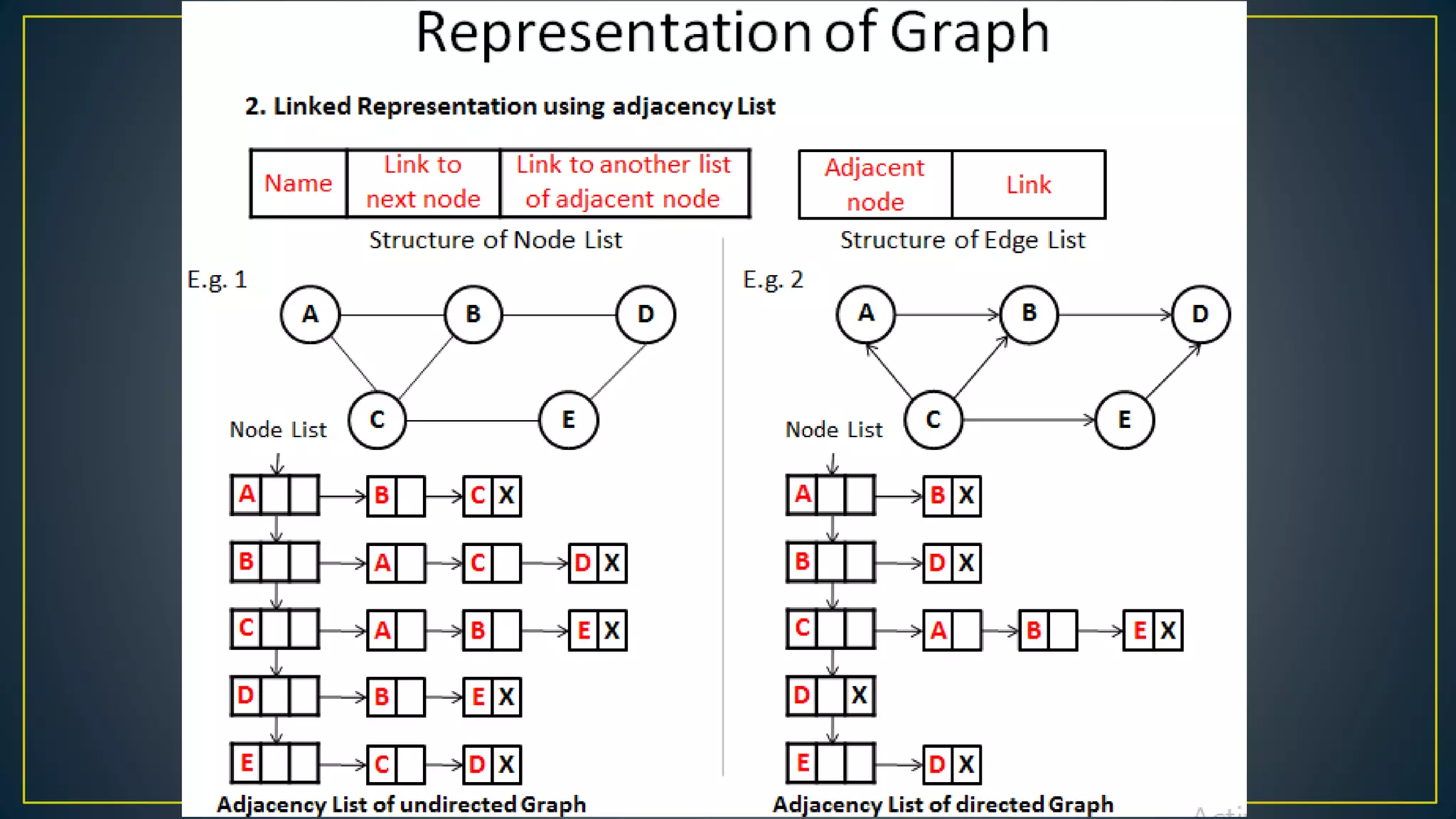
This document discusses data structures and algorithms related to trees and graphs. It begins by defining trees and describing their key properties like root, parent, child, leaf nodes, subtrees, levels, and tree traversal methods. It then discusses binary trees and their representations. The document also covers graph representations and key graph concepts like vertices, edges, paths, cycles, degrees. It describes traversal methods for graphs like depth first search and breadth first search. Finally, it discusses applications of trees and graphs in areas like routing, compression, and 3D graphics.

1. Data Structures and Algorithms
Unit - II

2. Unit II
Trees – Binary tree representations – Tree
Traversal – Threaded Binary Trees – Binary Tree
Representation of Trees – Graphs and
Representations – Traversals, Connected
Components and Spanning Trees – Shortest
Paths and Transitive closure – Activity Networks –
Topological Sort and Critical Paths.

3. • Atree is an abstract model of ahierarchical structure that consistsof
nodes with aparent-child relationship.
• Treeis asequence of nodes
• There is astarting node known asaroot node
• Everynode other than the root hasaparentnode.
• Nodes mayhaveany number of children

6. • Root −Node at the top of the treeis called root.
• Parent −Any node except root node has one edge upward to a node called parent.
• Child − Node below agiven node connected by its edge downward is called its child node.
• Sibling – Child of same node are called siblings
• Leaf −Node which does not have any child node is called leaf node.
• Subtree −Subtree represents descendants of a node.
• Levels −Level of anode represents the generation of anode. If root node is at level 0, then
itsnext child node is at level 1, its grandchild is at level 2 and soon.
• keys−Keyrepresents avalue of anode based on which asearch operation is to be carried
out for anode.

7. • Degree of anode:
• Thedegree of anode is the number of children of that node
• Degree of aTree:
• Thedegree of atree is the maximum degree of nodes in agiventree
• Path:
• It is the sequence of consecutive edges from source node to destination node.
• Height of anode:
• Theheight of anode is the maxpath length form that node to aleaf node.
• Height of atree:
• Theheight of atree is the height ofthe root
• Depth of atree:
• Depth of atree is the maxlevel of any leaf in the tree

9. • Non-linear data structure
• Combinesadvantages of an ordered array
• Searchingasfast asin ordered array
• Insertion and deletion asfast asin linked list
• Simple and fast

10. • Directory structure of afile store
• Structure of an arithmetic expressions
• Used in almost every 3D video game to determine what
objects need to be rendered.
• Used in almost every high-bandwidth router for storingrouter-
tables.
• used in compression algorithms, such asthose used by the .jpeg
and .mp3 file- formats.

11. • Abinary tree, is atree in which no node canhavemore than two
children.
• Consider abinary tree T
,here ‘A’is the root node of the binary treeT
.
• ‘B’ is the left child of ‘A’and ‘C’is theright
child of ‘A’
• i.e Ais afather of BandC.
• Thenode Band Care called siblings.
• Nodes D,H,I,F
,Jare leafnode

12. • Abinary tree, T,is either empty or suchthat
III.
I. Thasaspecial node called the root node
II. Thastwo sets of nodes L
Tand RT
,called the left subtree and right subtree of
T, respectively.
L
Tand RTare binarytrees.

13. • Abinary tree is a finite set of elements that are either empty or is
partitioned into three disjointsubsets.
• Thefirst subset contains asingle element called the root of the tree.
• Theother two subsets are themselves binary trees called the left and right
sub-trees of the originaltree.
• Aleft or right sub-tree canbeempty.
• Eachelement of abinary tree is called anode of thetree.

15. • Theroot node of this binary tree isA.
• Theleft sub tree of the root node, which we denoted by LA,is theset
LA ={B,D,E,G}and the right sub tree of the root node, RAis the set
RA={C,F
,H}
• Theroot node of LAis node B,the root node of RAis Cand soon

16. • Complete binary tree
• Strictly binary tree
• Almost complete binary tree

17. • If every non-leaf node in abinary tree hasnonempty leftand right sub-trees, then
suchatree is called astrictly binarytree.
• Or,to put it another way,all of the nodes in astrictly binary tree are of degree zero
or two, never degreeone.
• Astrictly binary tree with
Nleavesalwayscontains 2N– 1 nodes.

18. • Acompletebinarytree is abinarytree in which every level, except possiblythe last, is completely
filled, and all nodes are asfar leftaspossible.
• Acompletebinarytreeof depth d is called strictly binary tree if all of whose leavesare at level d.
• Acomplete binary tree has2d nodes at every depthd and 2d -1 non leaf nodes

19. • Analmost complete binary tree is atree where for aright child, thereis alwaysa
left child, but for aleft child there may not be aright child.

22. • Traversalis aprocessto visit all the nodes of atree and mayprinttheir
values too.
• All nodes are connected via edges(links) we alwaysstart from theroot
(head)node.
• There are three wayswhich we useto traverse atree
• In-orderTraversal
• Pre-orderTraversal
• Post-orderTraversal
• Generally we traverse atree to search or locate given item or keyin the tree
or to print all the values it contains.

23. • Pre-order
<root><left><right>
• In-order
<left><root><right>
• Post-order
<left><right><root>

24. • Thepreorder traversal of anonempty binary tree is defined asfollows:
• Visit the root node
• Traversethe left sub-tree inpreorder
• Traversethe right sub-tree inpreorder

25. • Thein-order traversal of anonempty binary tree is defined asfollows:
• Traversethe left sub-tree inin-order
• Visit the root node
• Traversethe right sub-tree ininorder
• Thein-order traversal output
of the given treeis
H D I B E A F C G

26. • Thein-order traversal of anonempty binary tree is defined asfollows:
• Traversethe left sub-tree inpost-order
• Traversethe right sub-tree inpost-order
• Visit the root node
• Thein-order traversal output
of the given treeis
H I D E B F G C A

27. • A binary search tree (BST) is a binary tree that is either empty or in
which every node contains a key (value) and satisfies the following
conditions:
• All keys in the left sub-tree of the root are smaller than the key in the root
node
• All keysin the right sub-tree of the root are greater than the keyin the root
node
• Theleft and right sub-trees of the root are again binary search trees

29. • Abinary search tree is basically abinary tree, and therefore it canbe
traversed in inorder, preorder andpostorder.
• If we traverse abinary search tree in inorder and print the identifiers
contained in the nodes of the tree, we get asorted list of identifiers in
ascending order.

30. • Following operations canbe done in BST
:
• Search(k,T):Searchfor keyk in the tree T
.If k is found in somenode oftree
then return true otherwise returnfalse.
• Insert(k,T):Insert anew node with value k in the info field in the tree Tsuch
that the property of BSTismaintained.
• Delete(k, T):Delete anode with value k in the info field from the tree Tsuch
that the property of BSTismaintained.
• FindMin(T), FindMax(T): Find minimum and maximum element from the
given nonempty BST
.

35. Graph is a non Linear Data structure which is a collection of two finite sets of V & E
Where V is vertices(node) and E is Edges (arcs)
i.e. G = (V, E)
Where V = {A, B, C, D, E, F} &
E = { (A, B}, (A,C), (B,C), (B,D), (C,D), (C,E), (D,E), (D,F), (E,F)}
The pair (A,B) defines an edge between A and B.
A
E.g. B D
C E F
The number of vertices of graph constitute the order of graph. Hence In given
Example the order of graph is Six

36. 1. Adjacent vertices: Two vertices are said to be adjacent if they are connected by an edge.
e.g. B & C
2. Adjacent Edges: Two edges are said to be adjacent if they are incident on the common
vertex.
e.g. CD & CE.
3. Path: A Path is a sequence of distinct vertices in which each vertex is adjacent to next one.
e.g. ABCDEF
4. Cycle: A cycle is a path consisting of at least three vertices where last vertex is adjacent to
the first vertex.
e.g. C D F E C
5. Loop: It is special cycle that start and end with same vertex without visiting any other vertex.
6. Degree of Vertex: The degree of a vertex is the number of lines incident on it
e.g. degree of D is 4
7. Out-Degree: The out Degree of directed graph is the number of arcs leaving the vertex.
8. In-Degree: In degree of directed graph is number of arcs entering the vertex.
9. Multiple Edges: The distinct parallel edges that connect the same end point.2