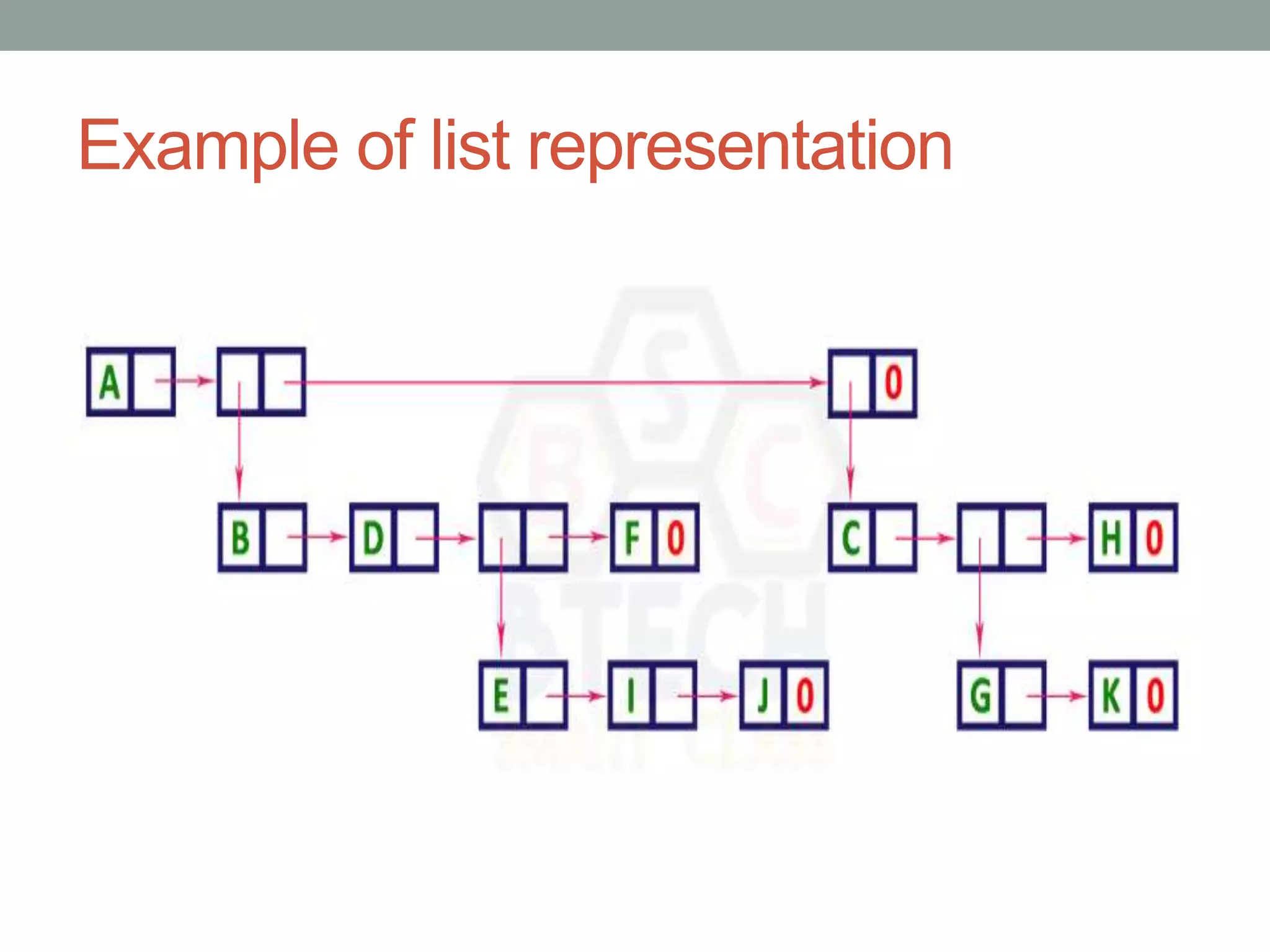
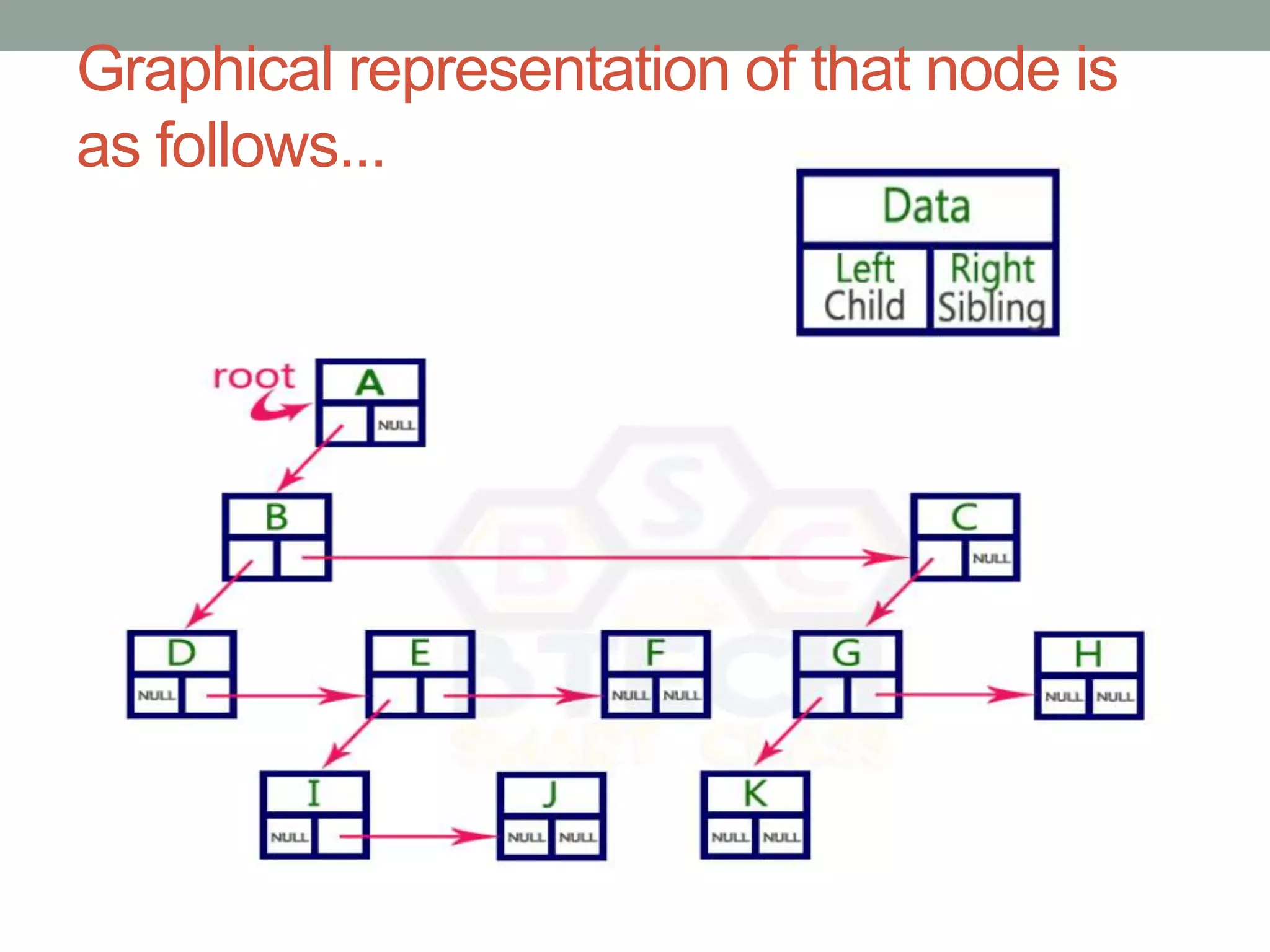
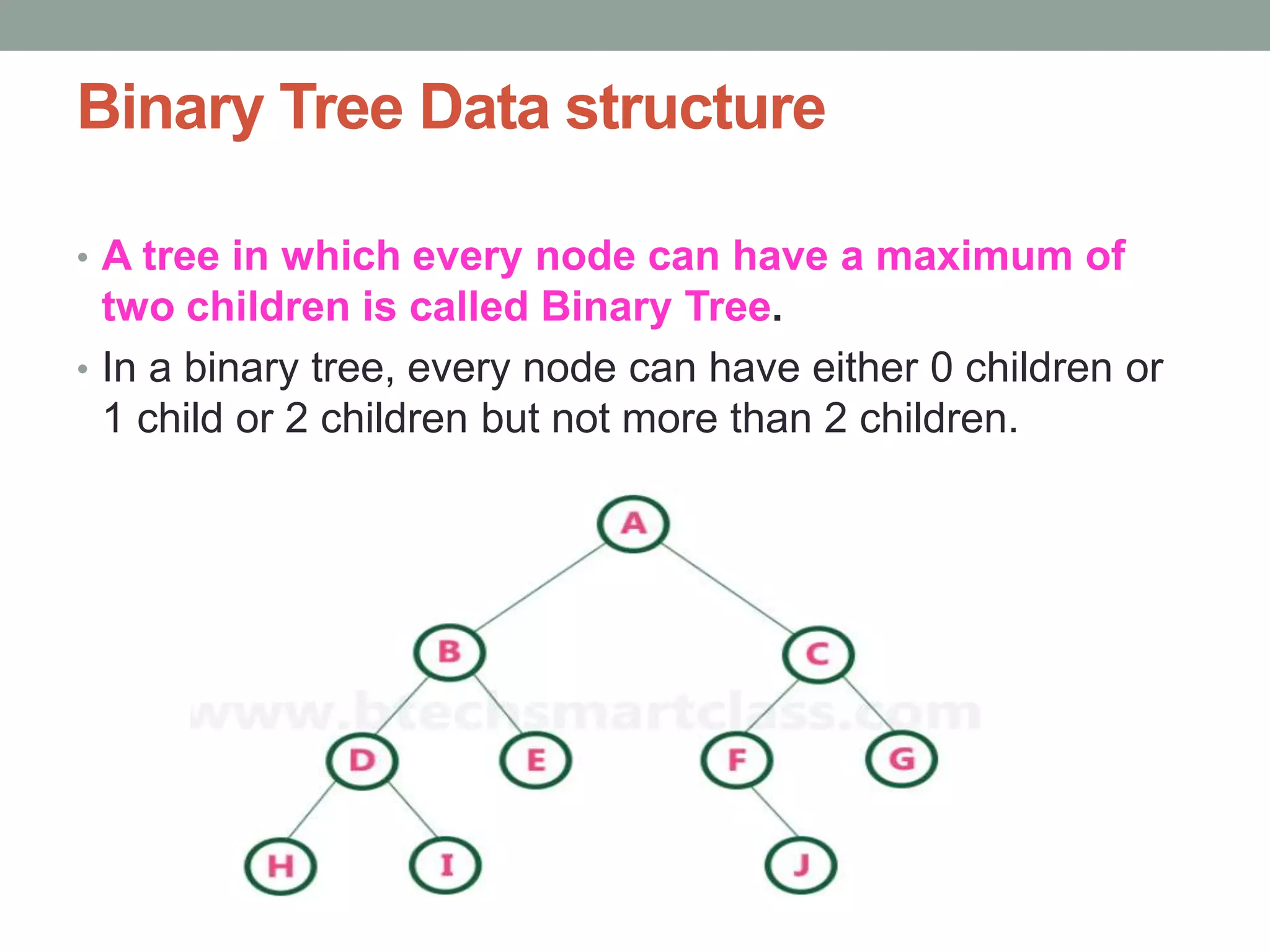
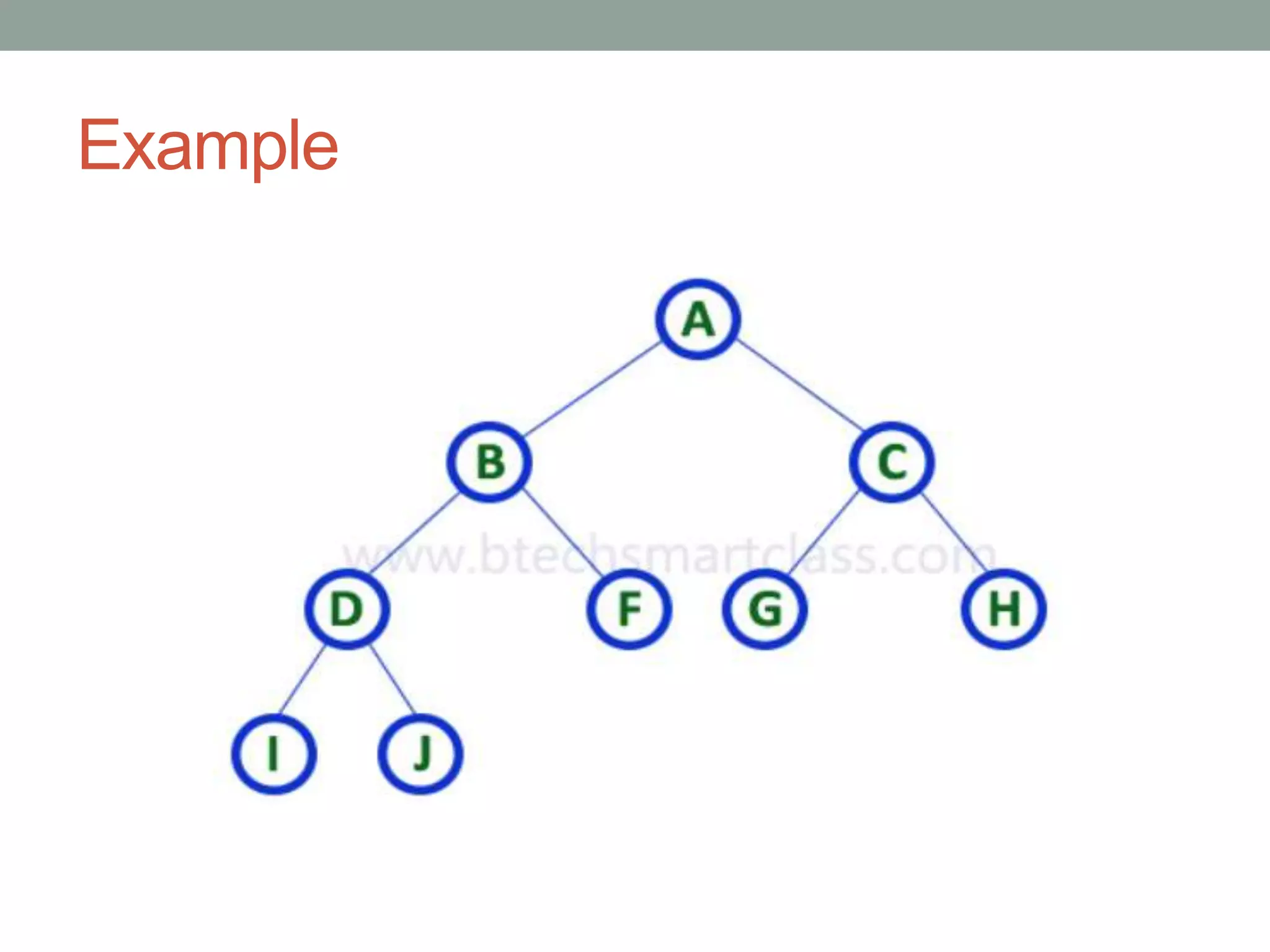
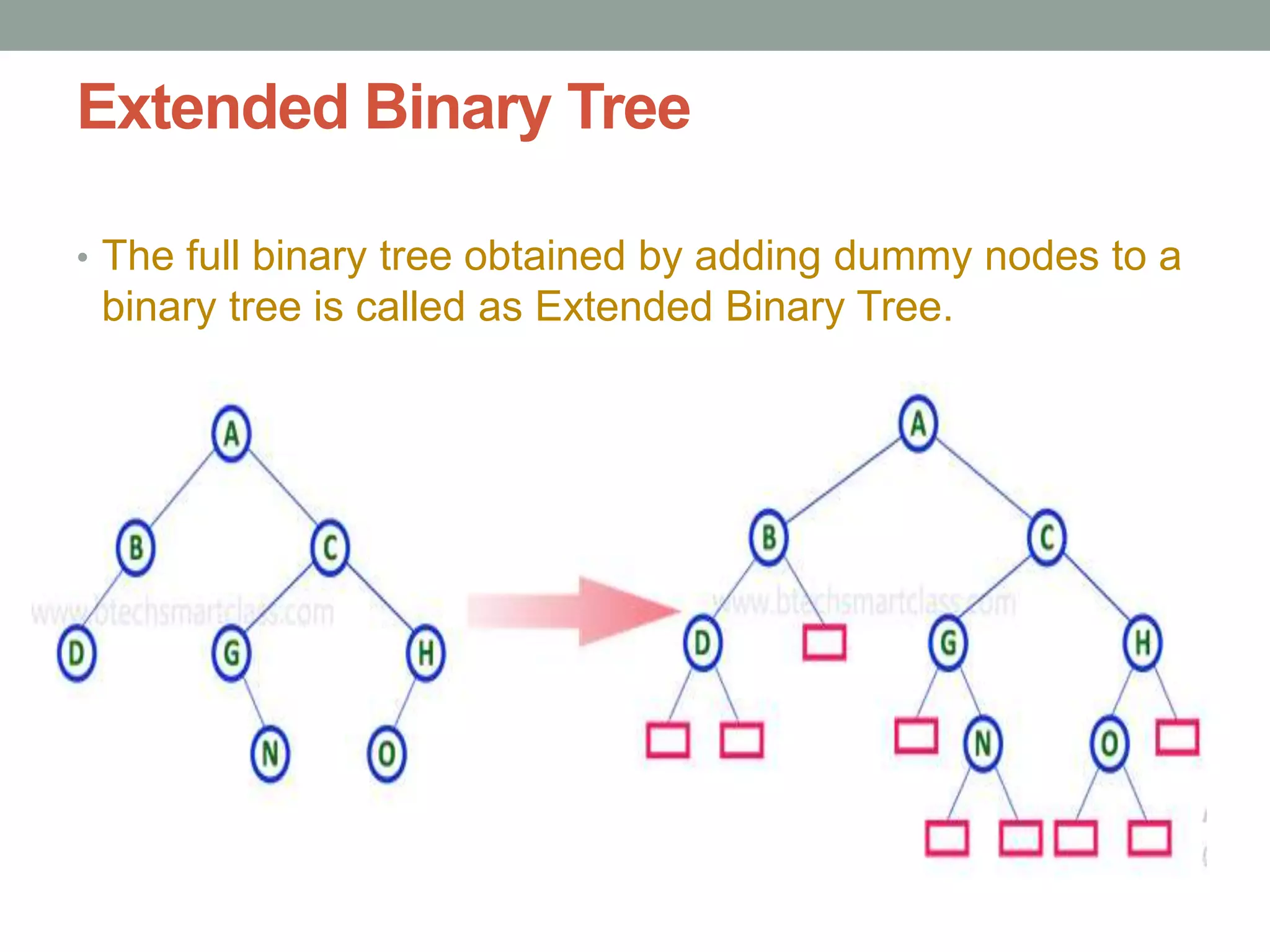
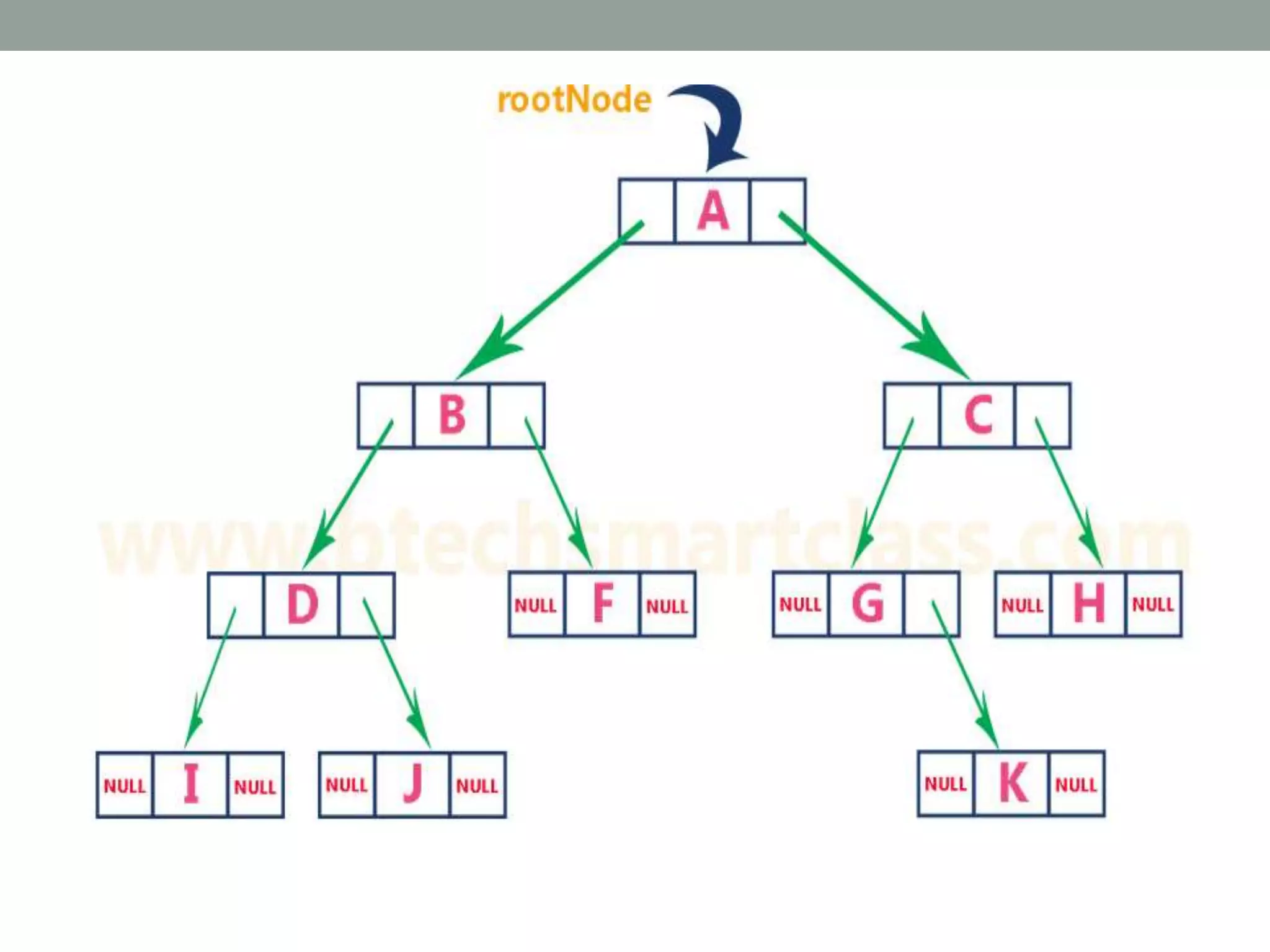
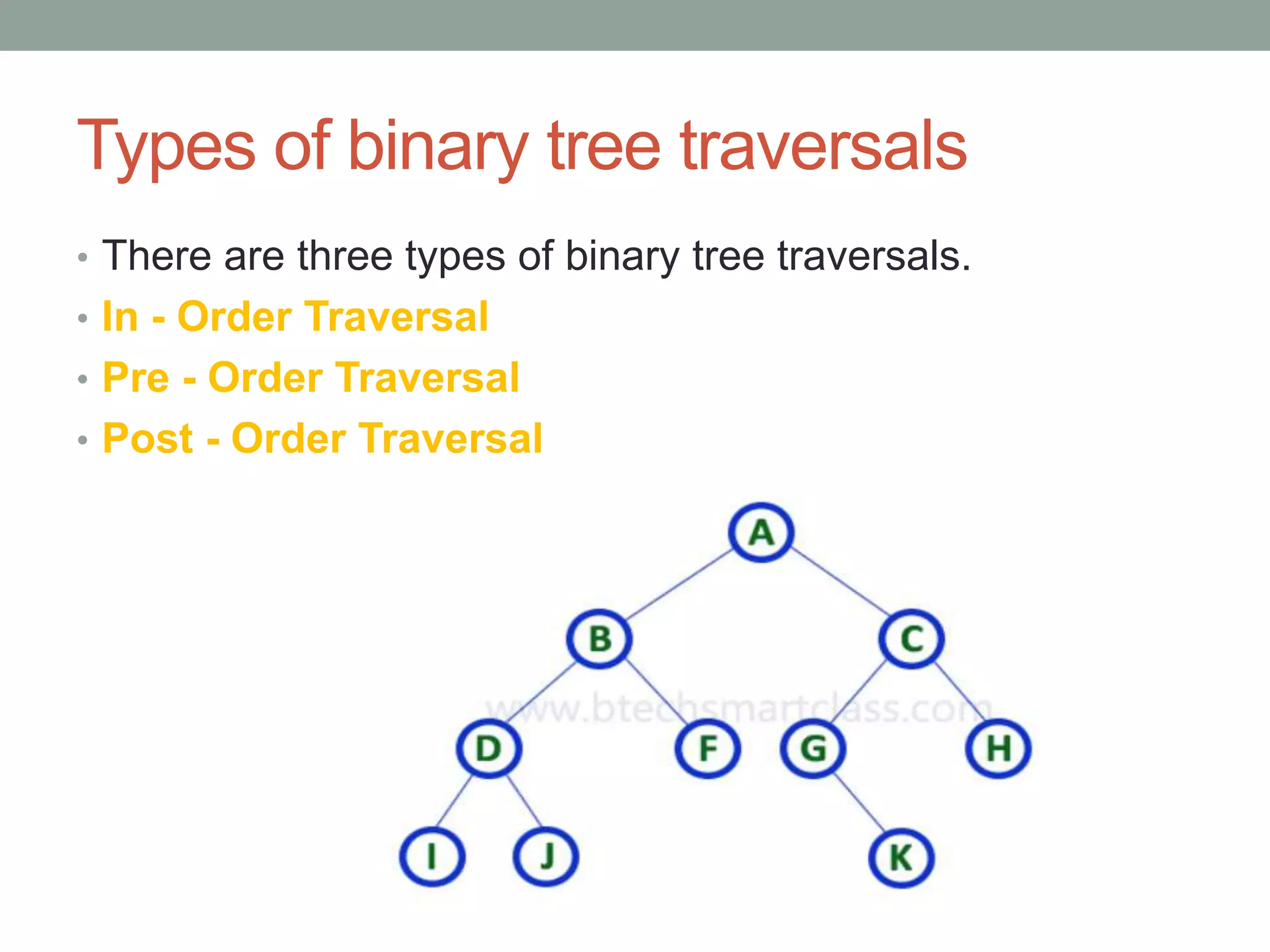
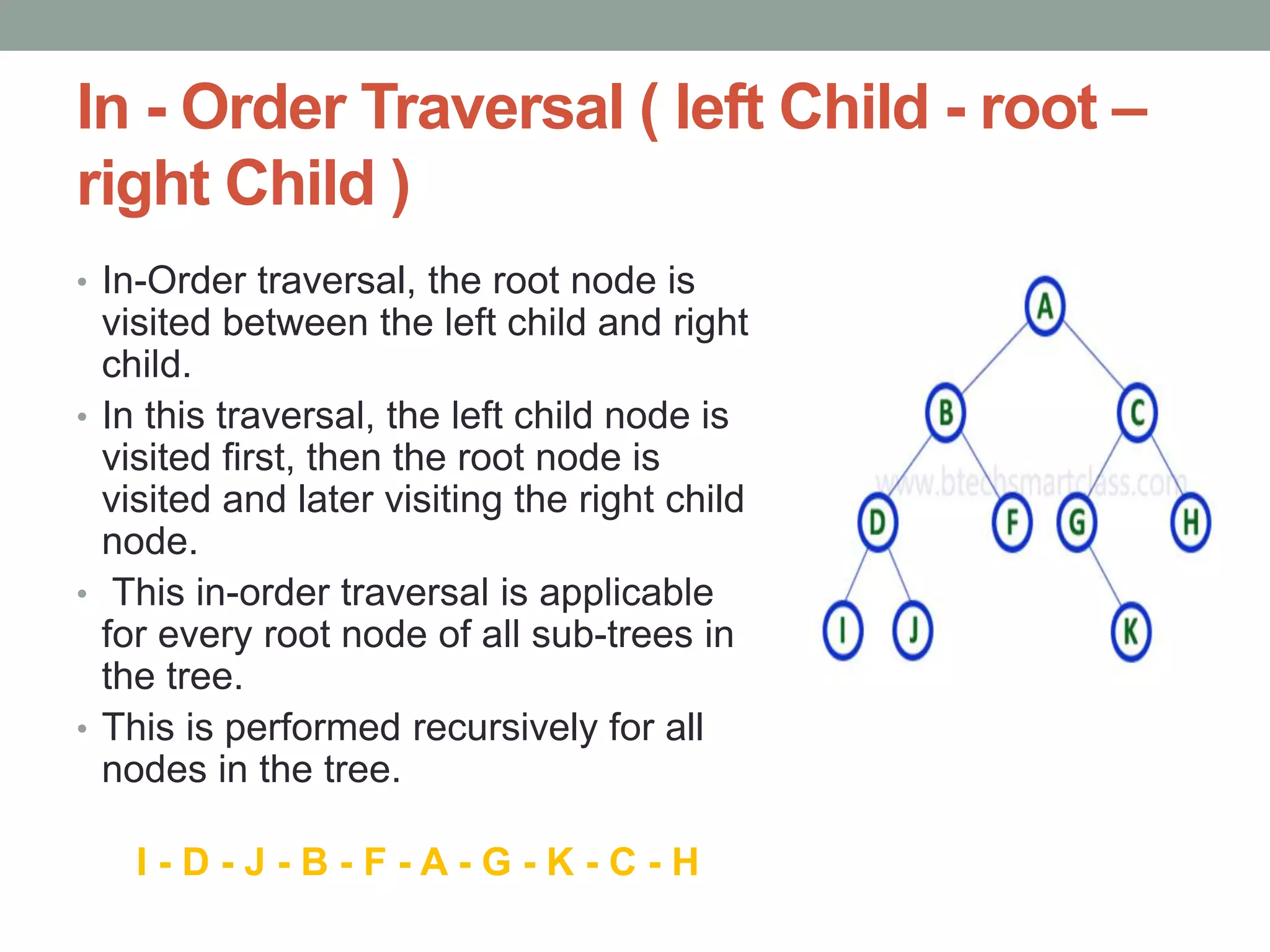
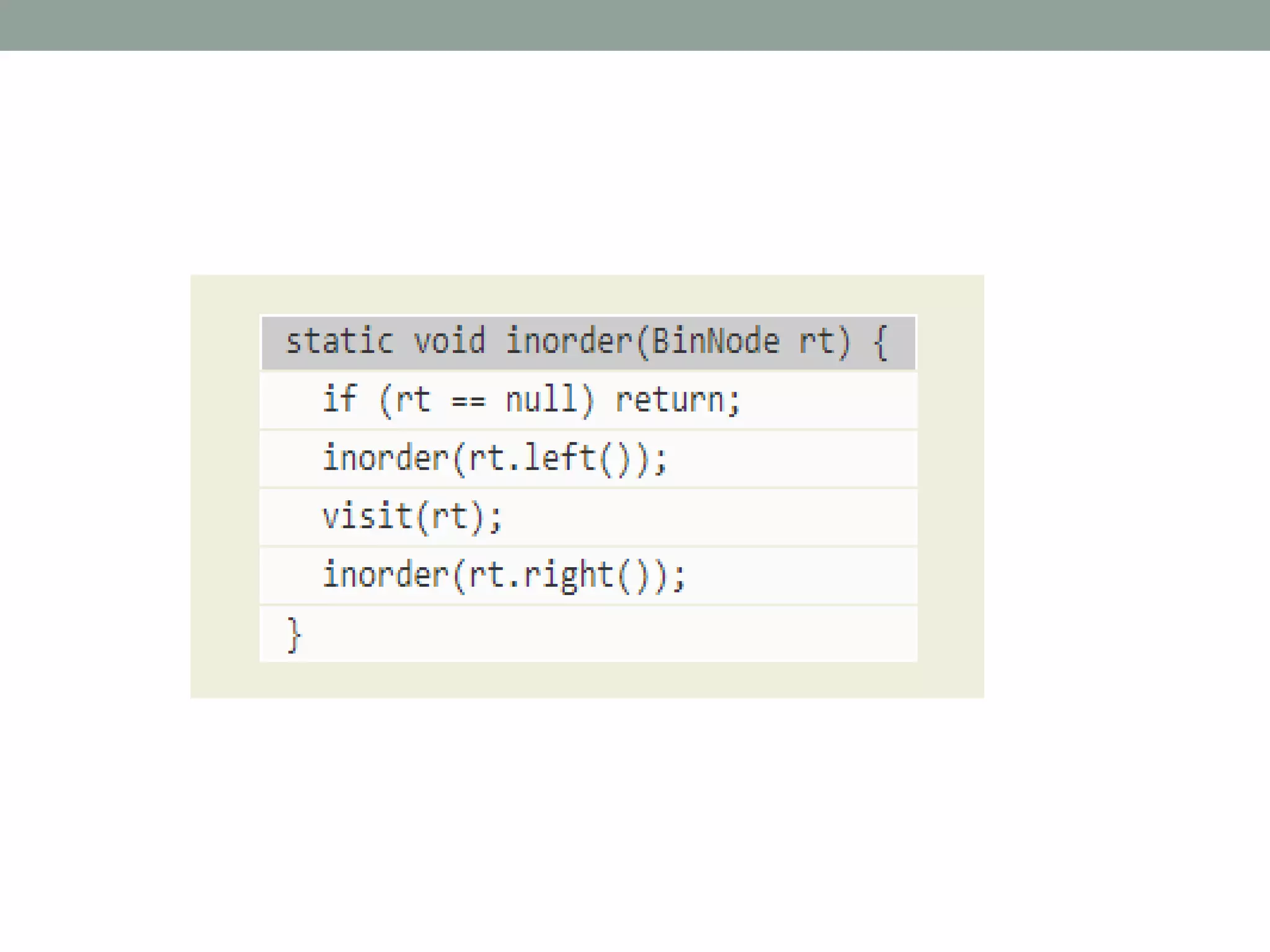
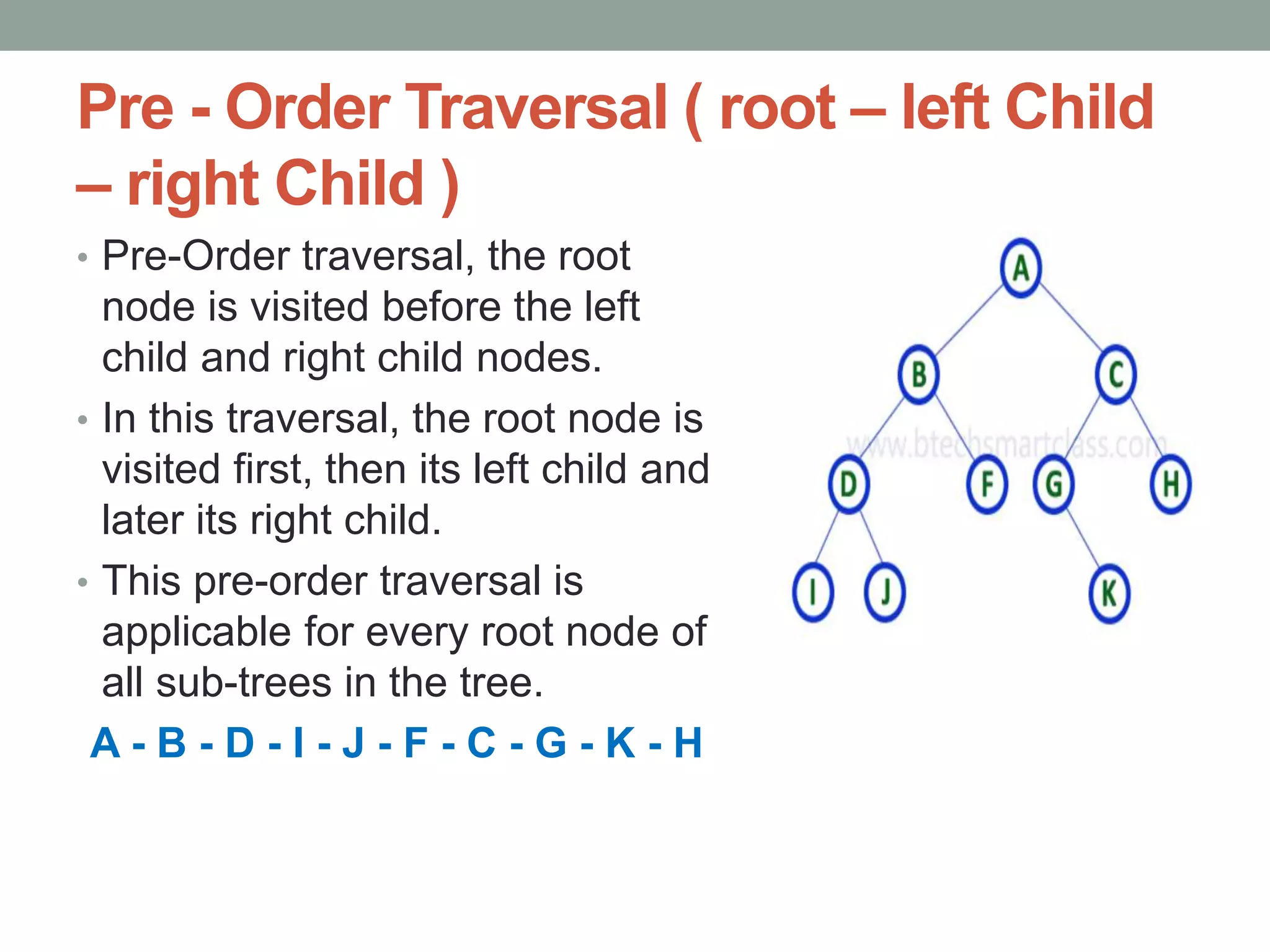
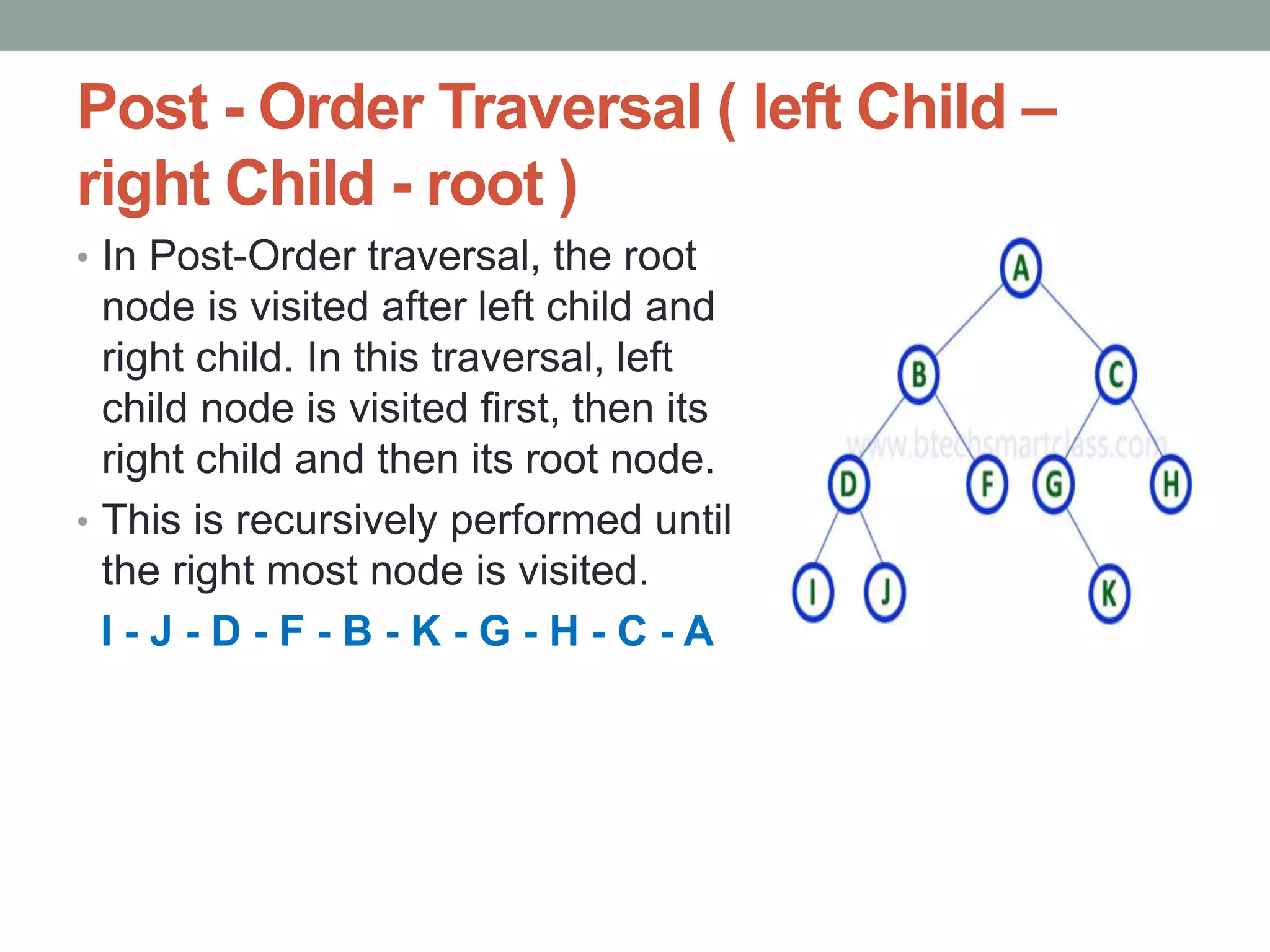
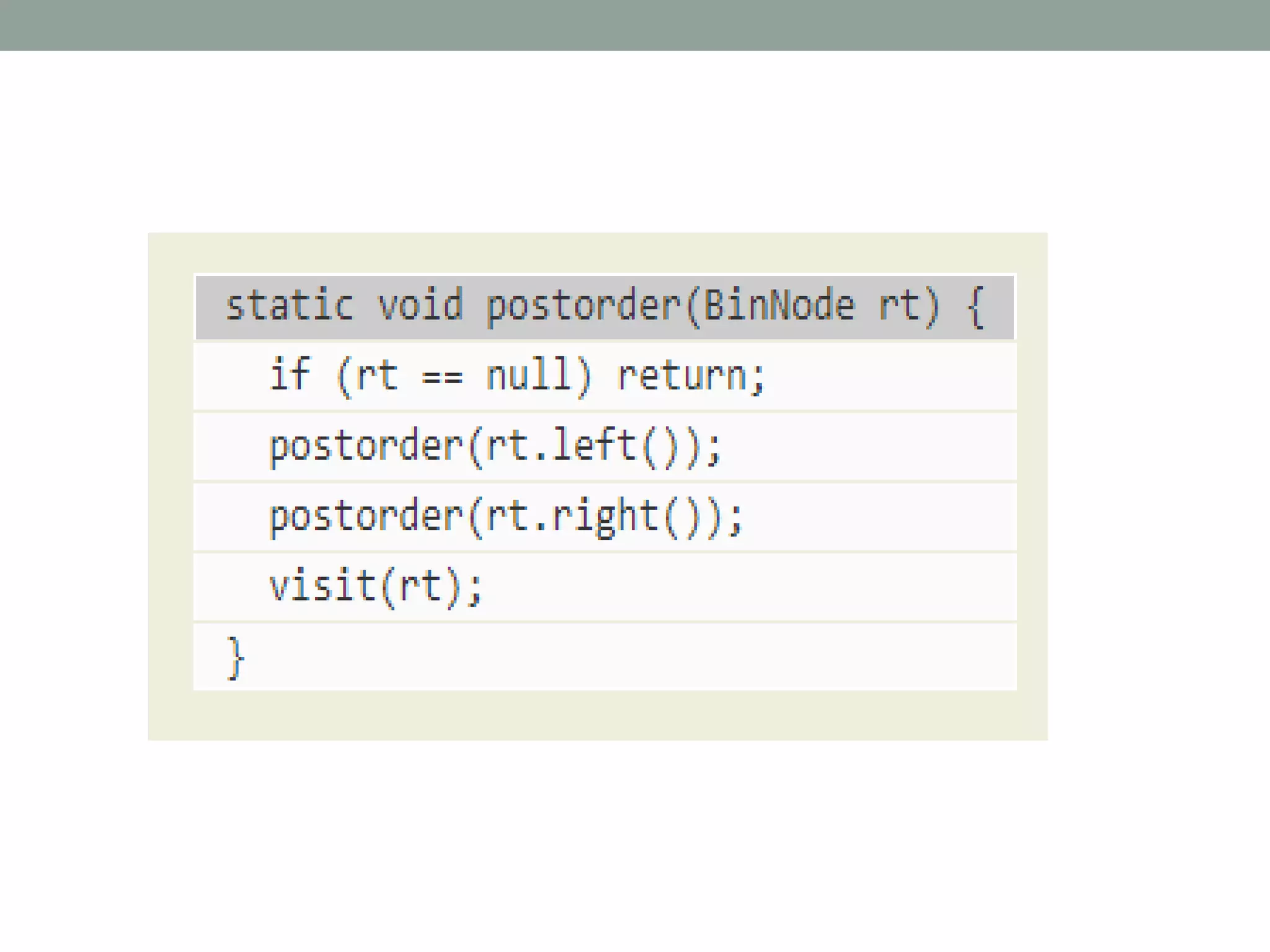
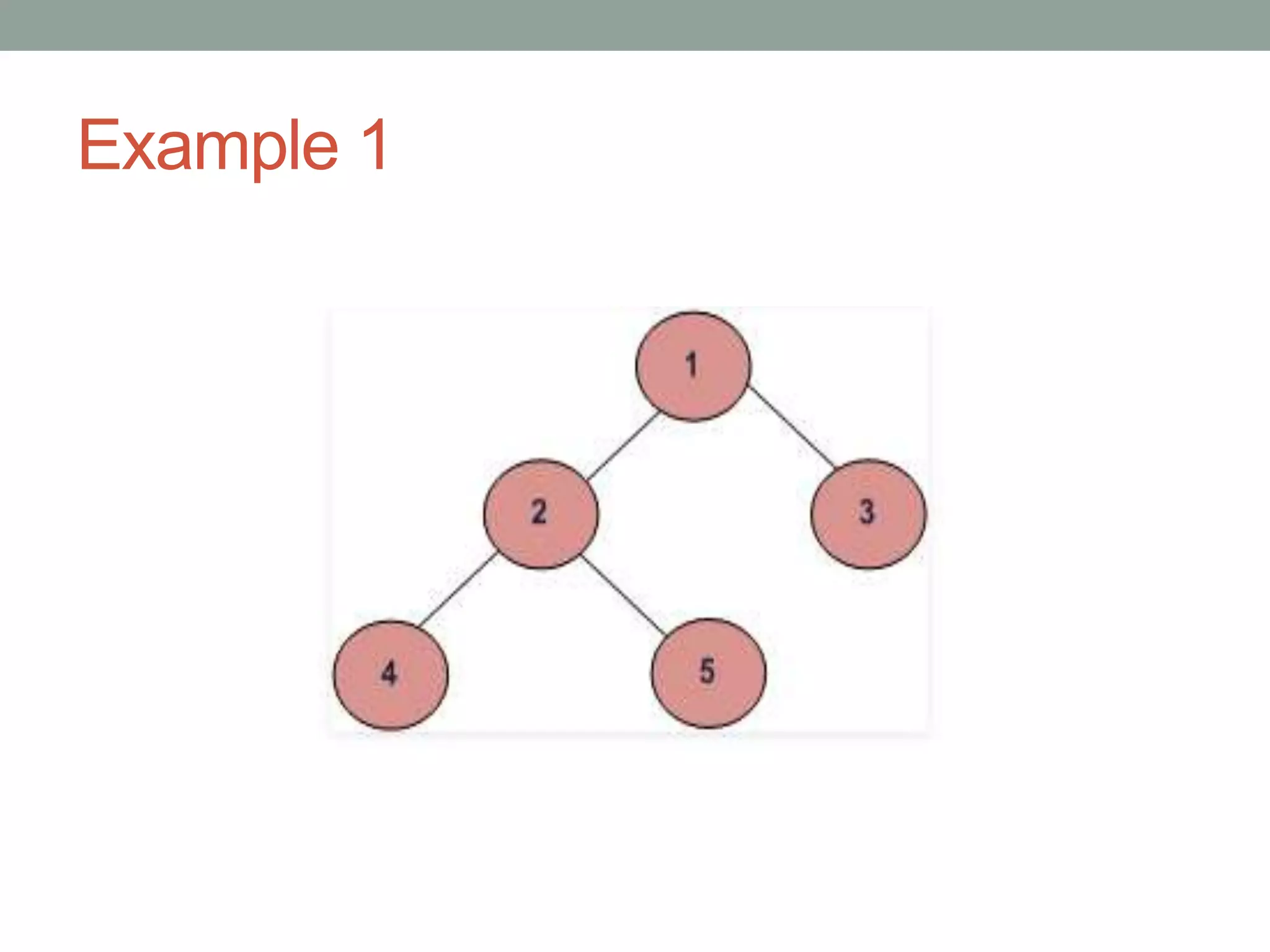
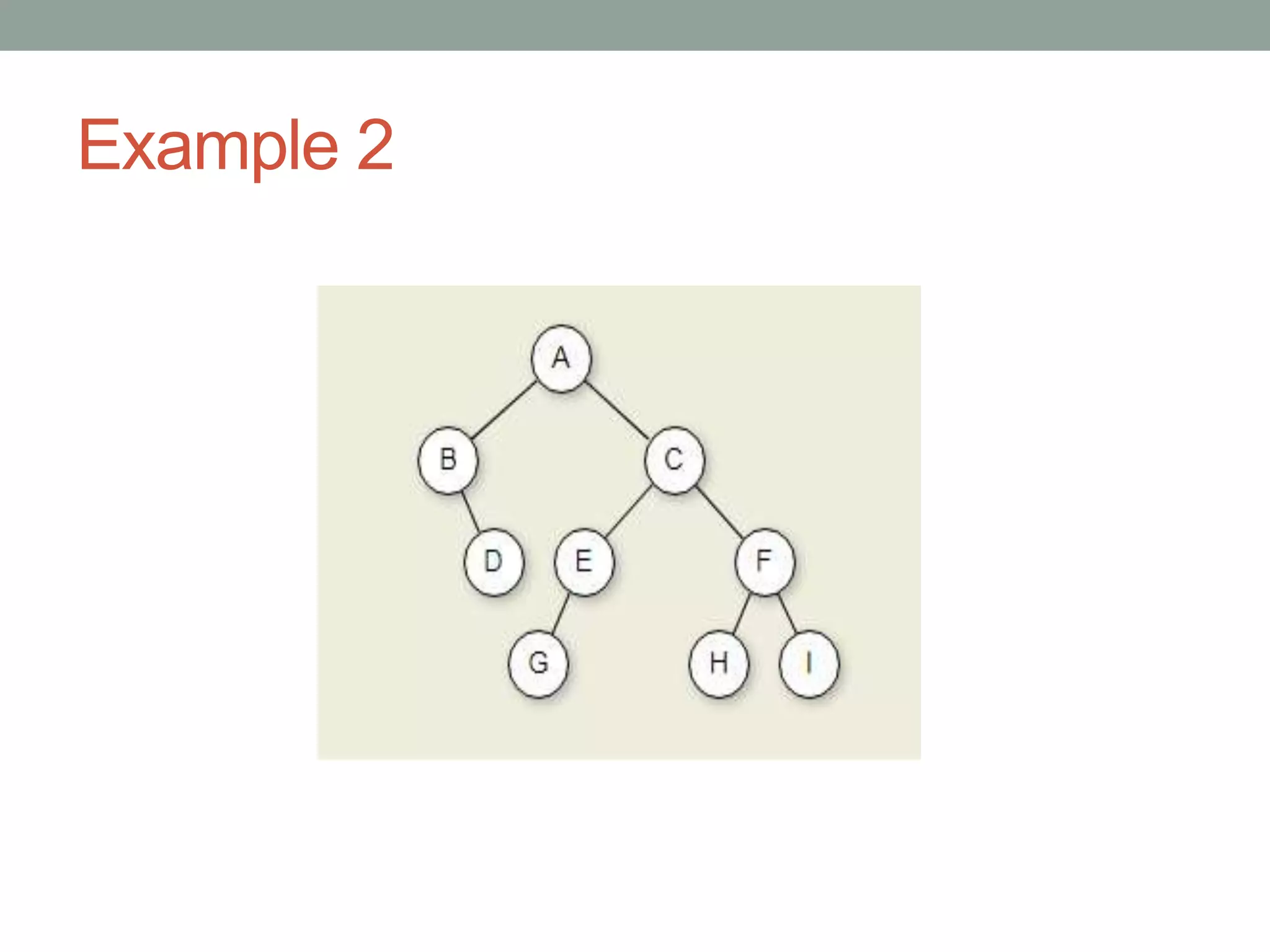
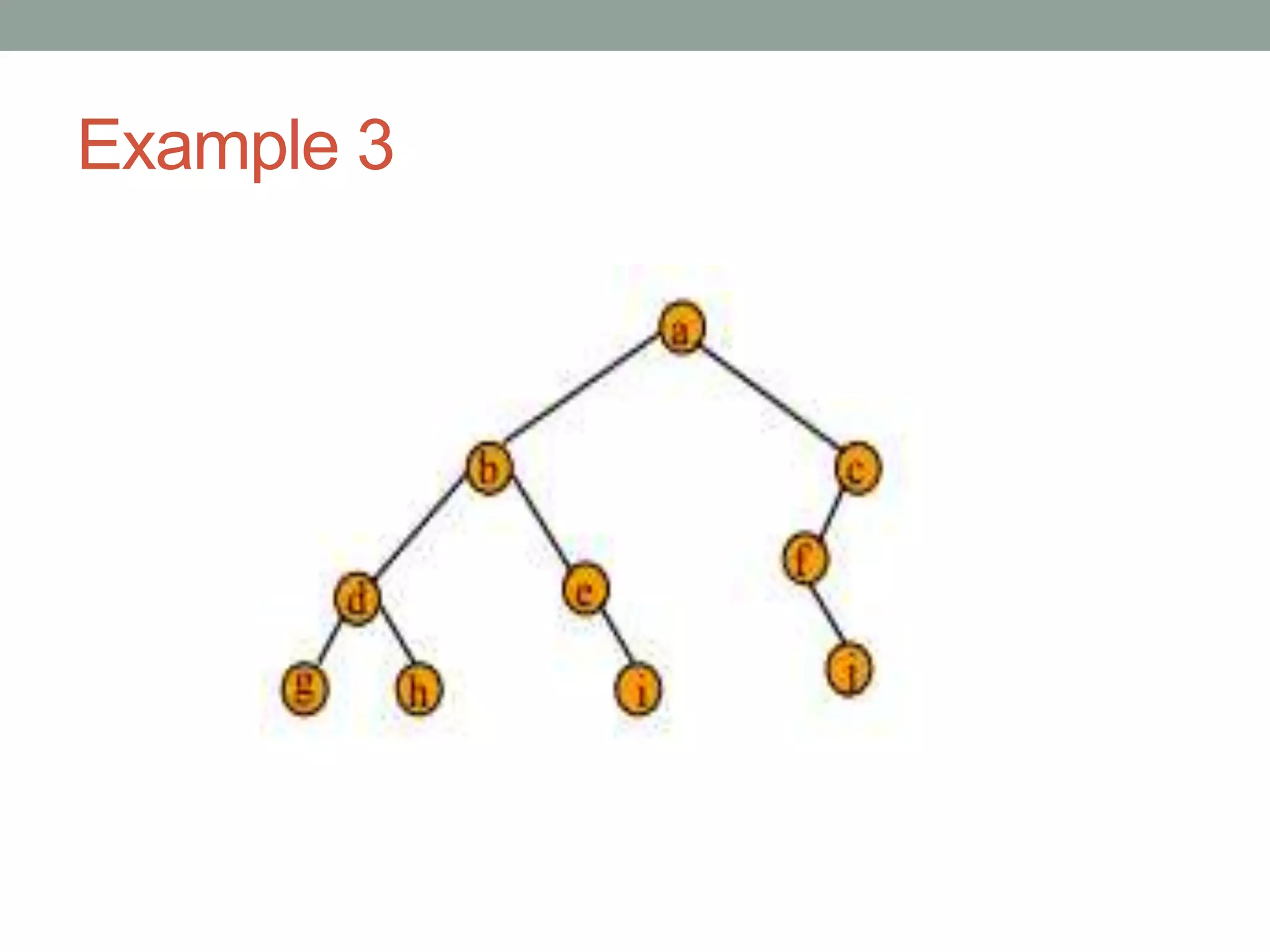
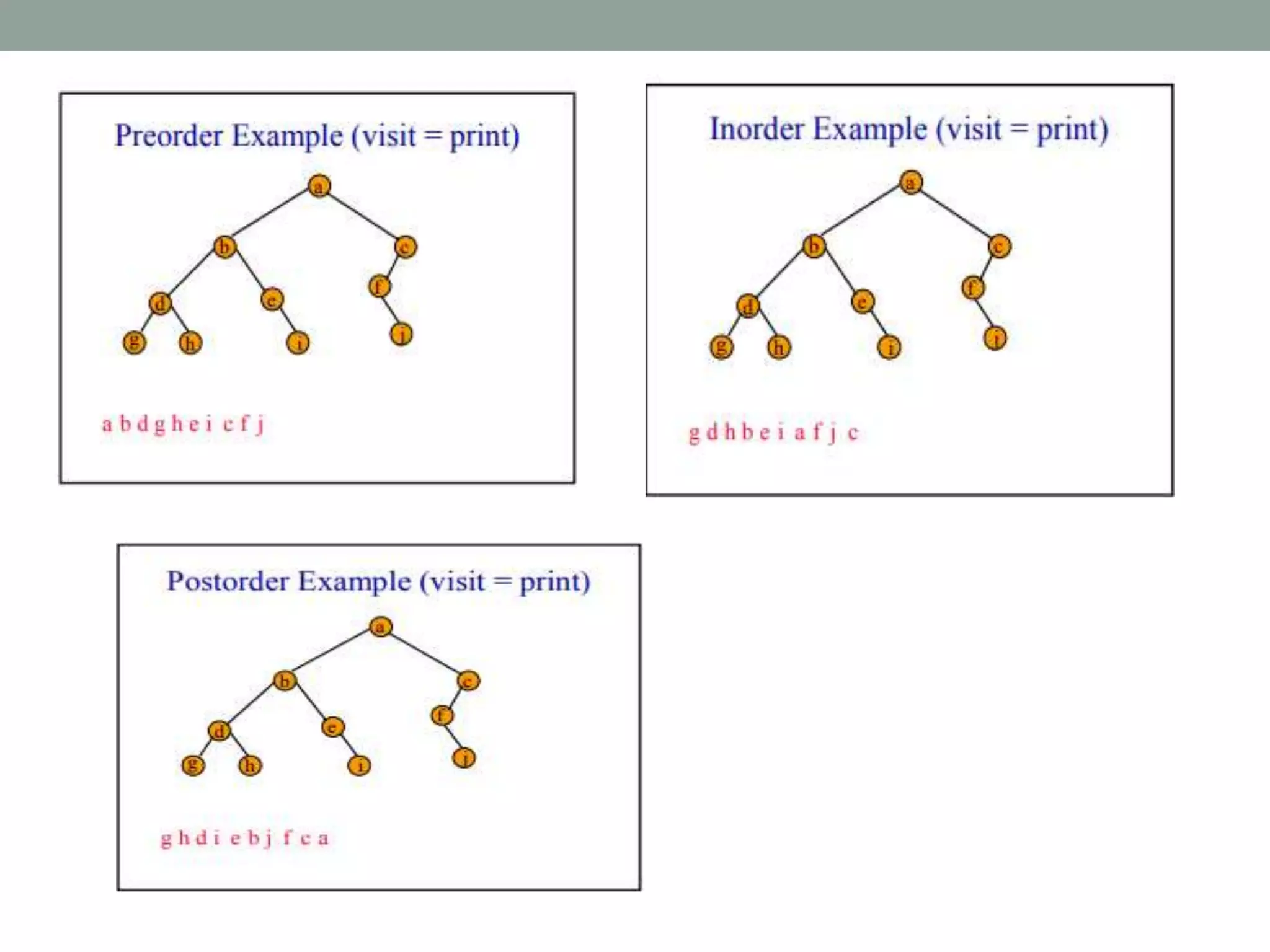
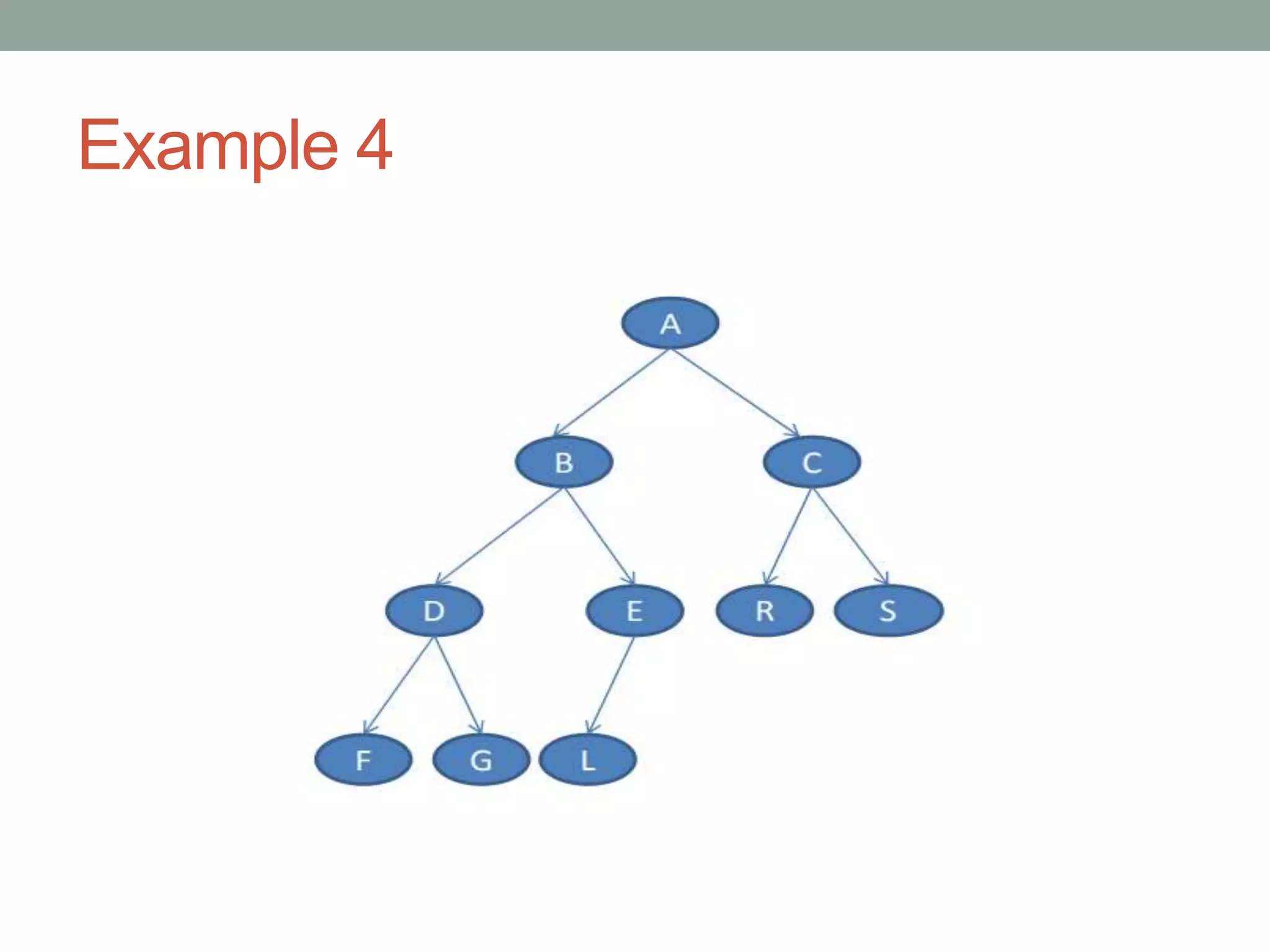
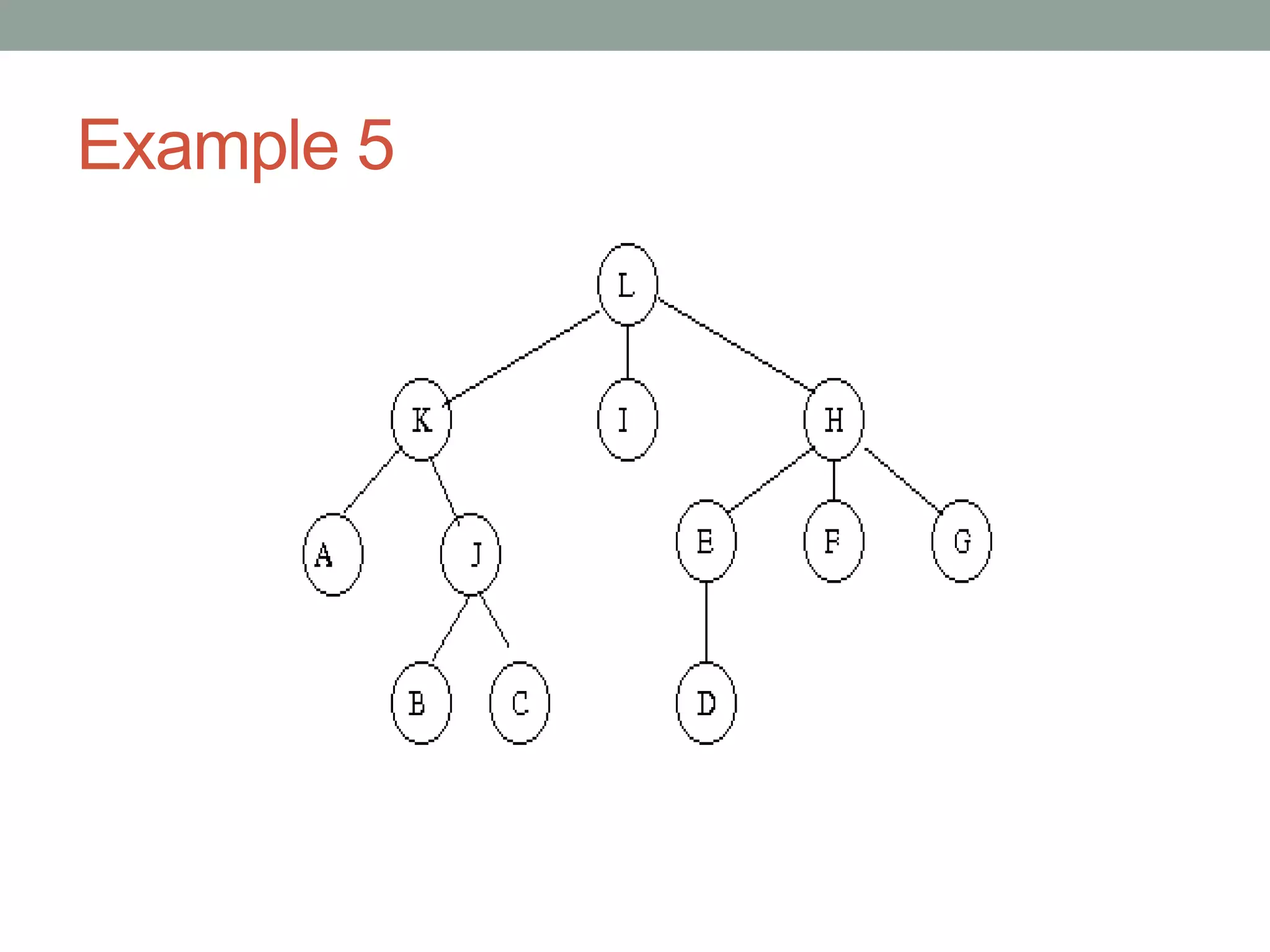
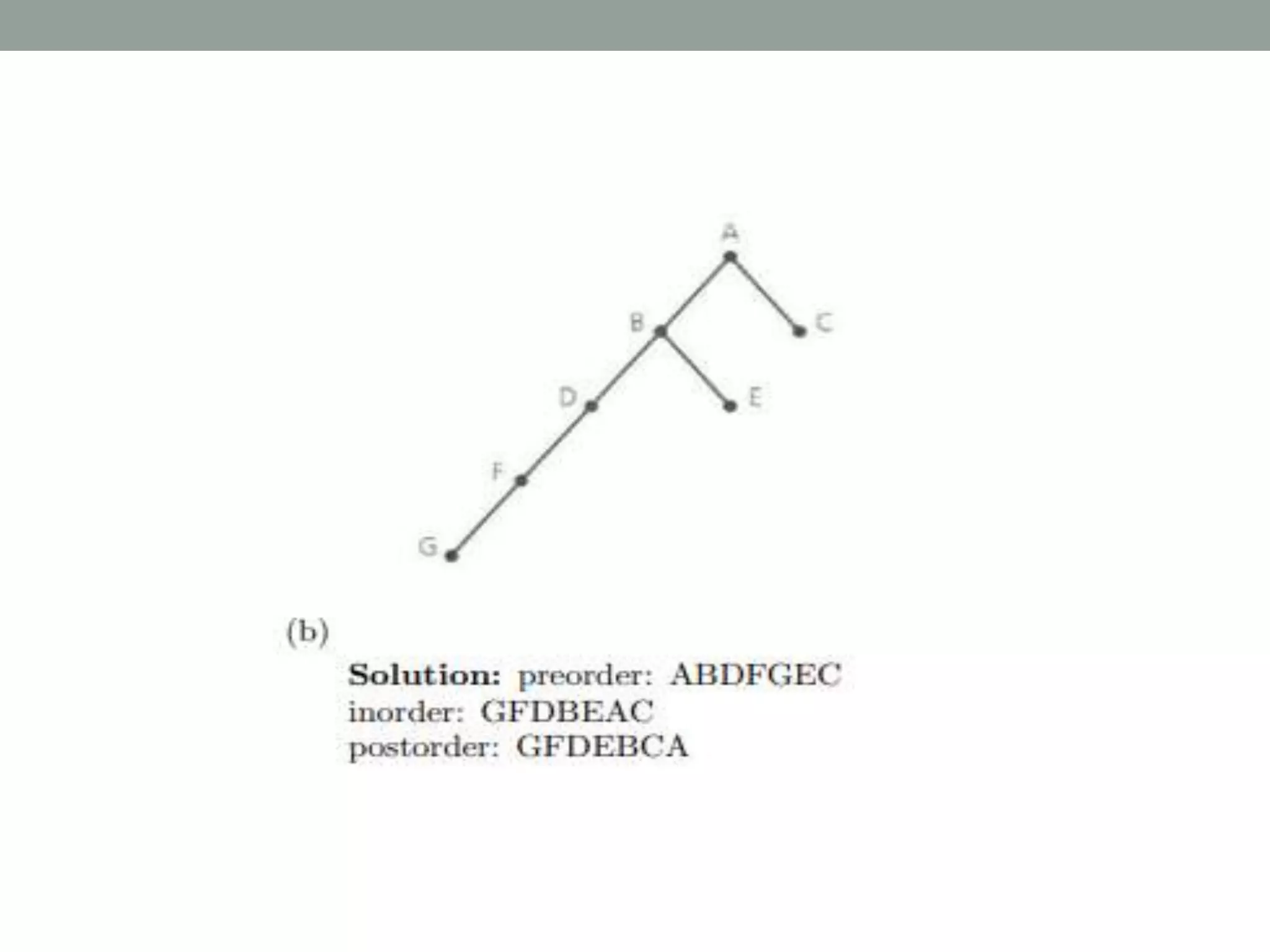
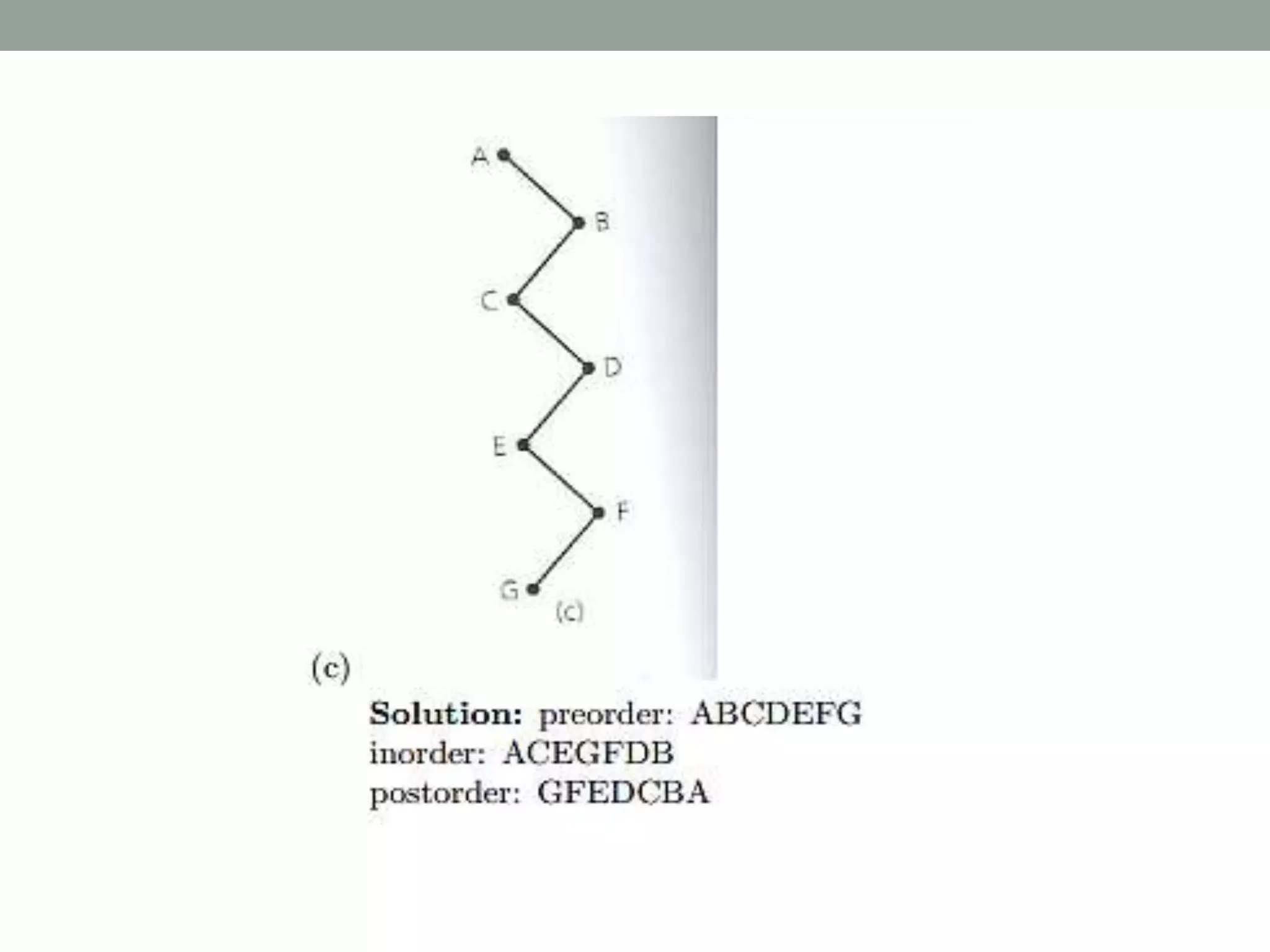
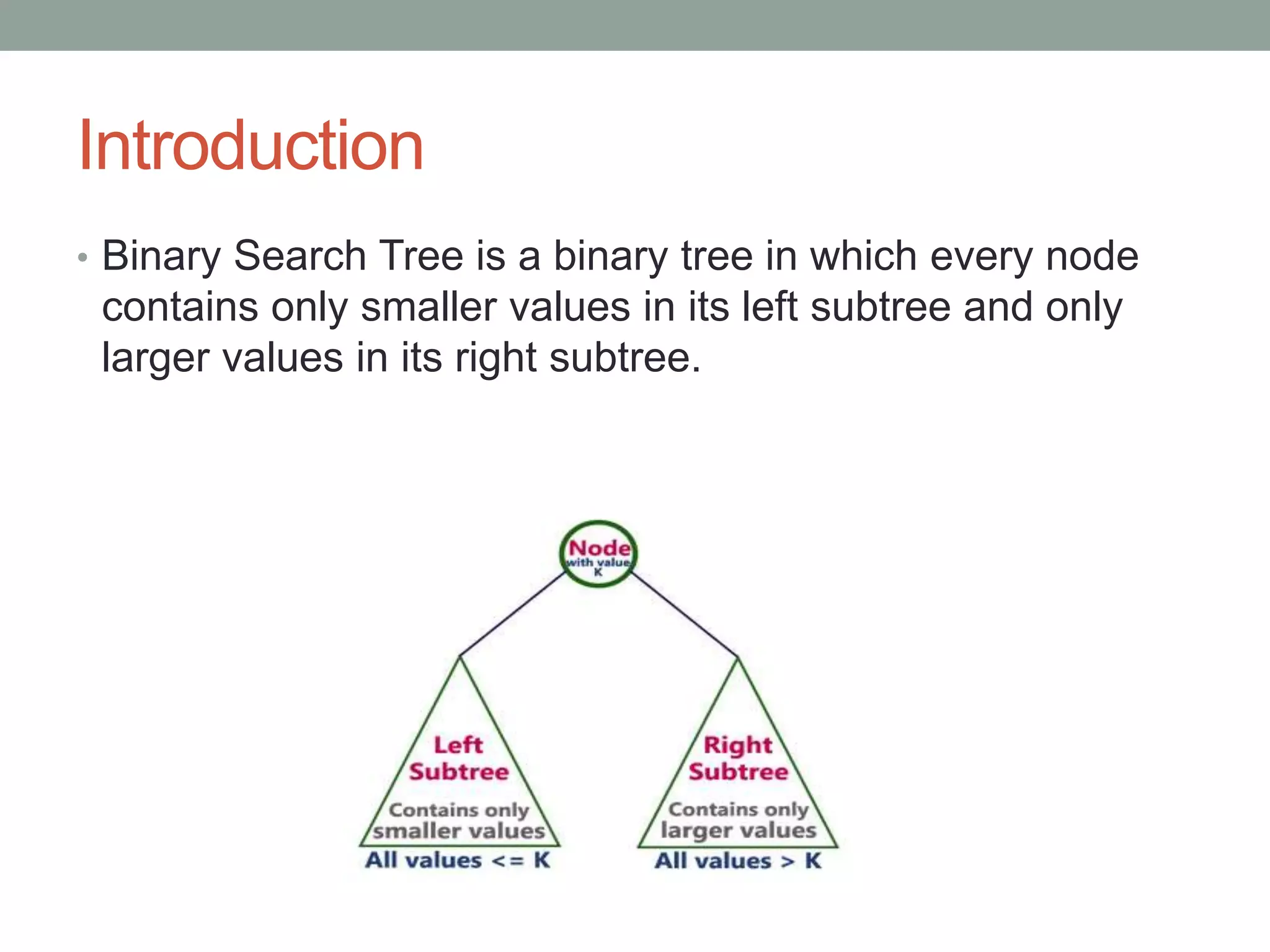
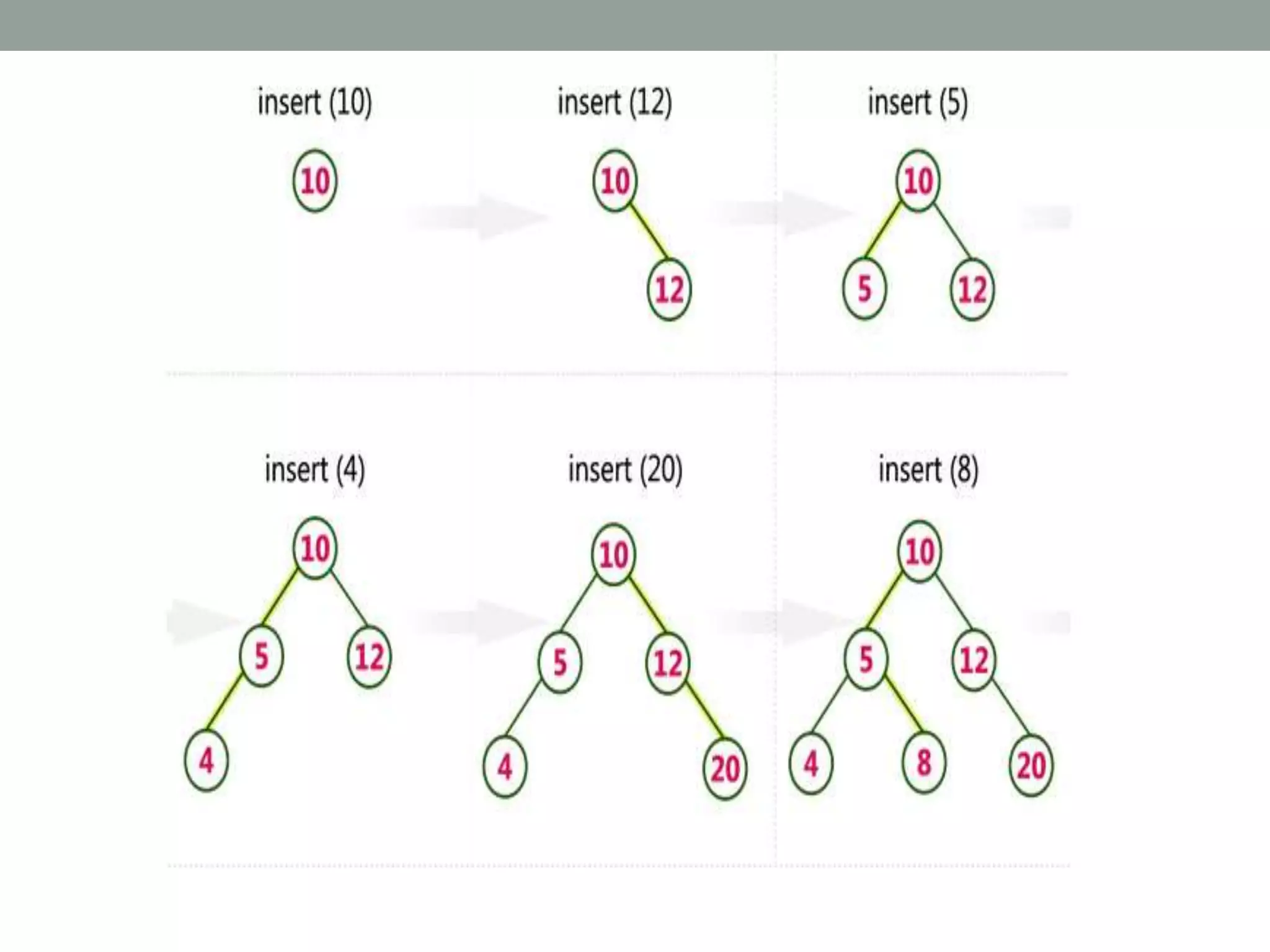
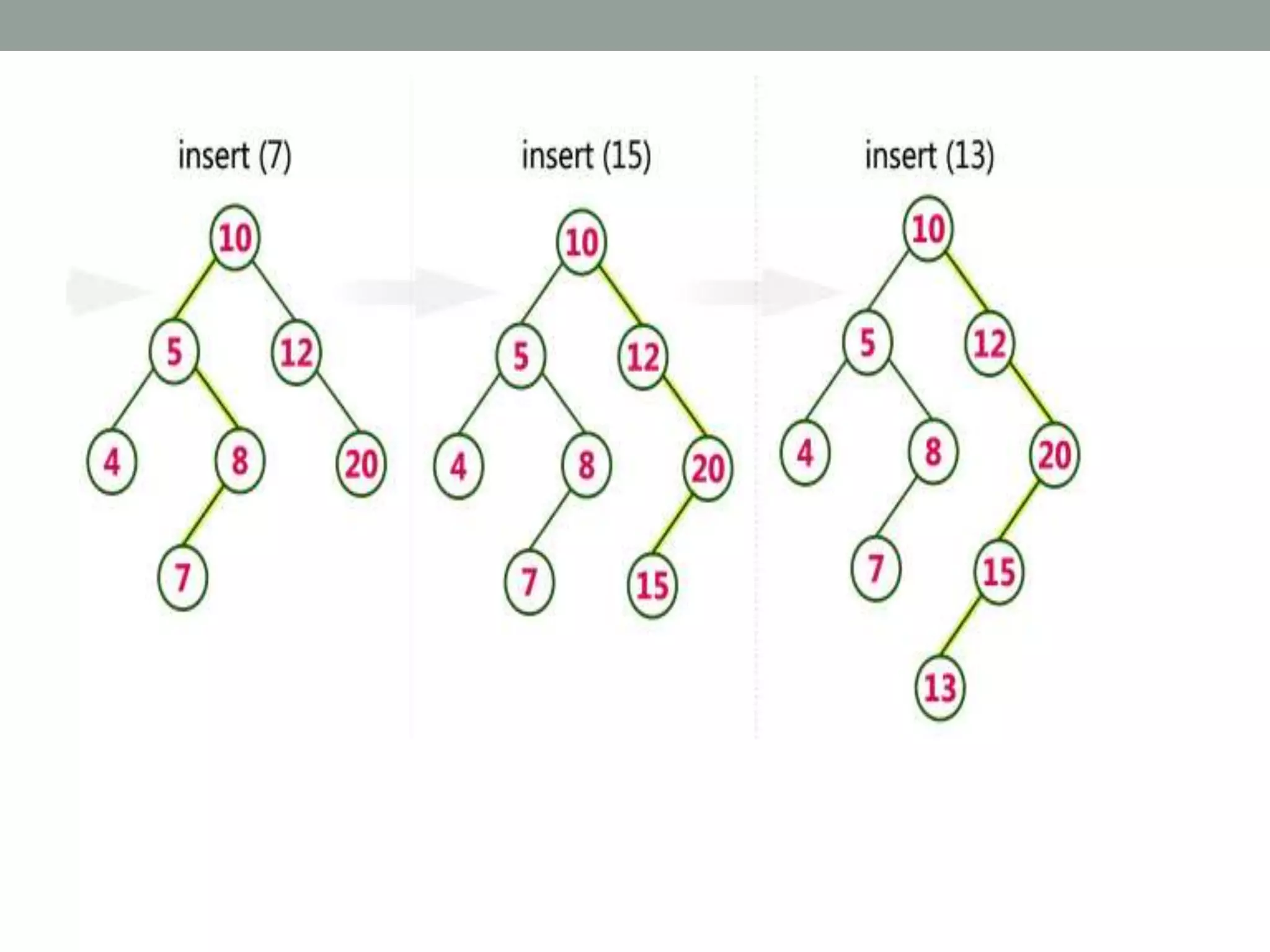
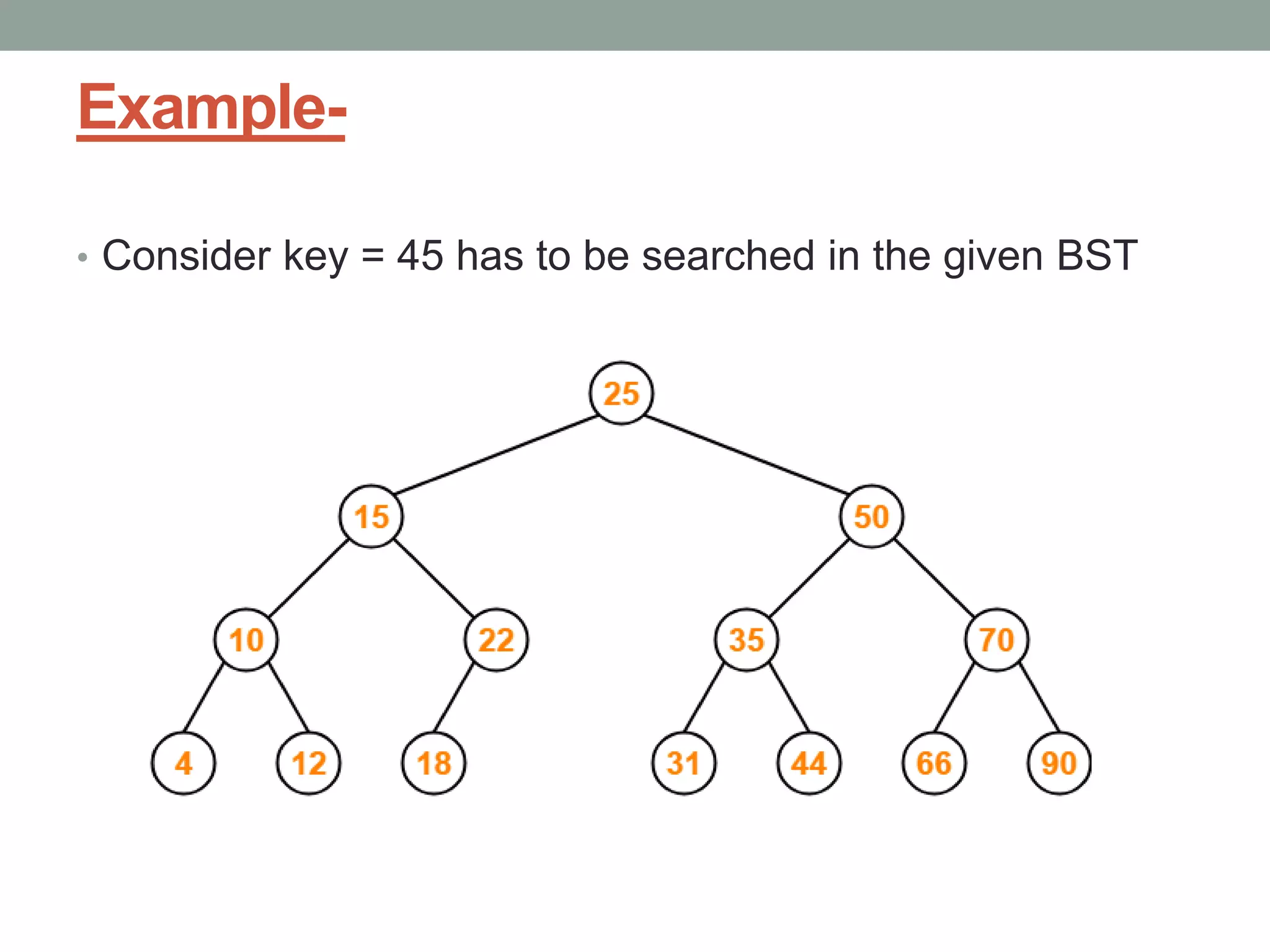
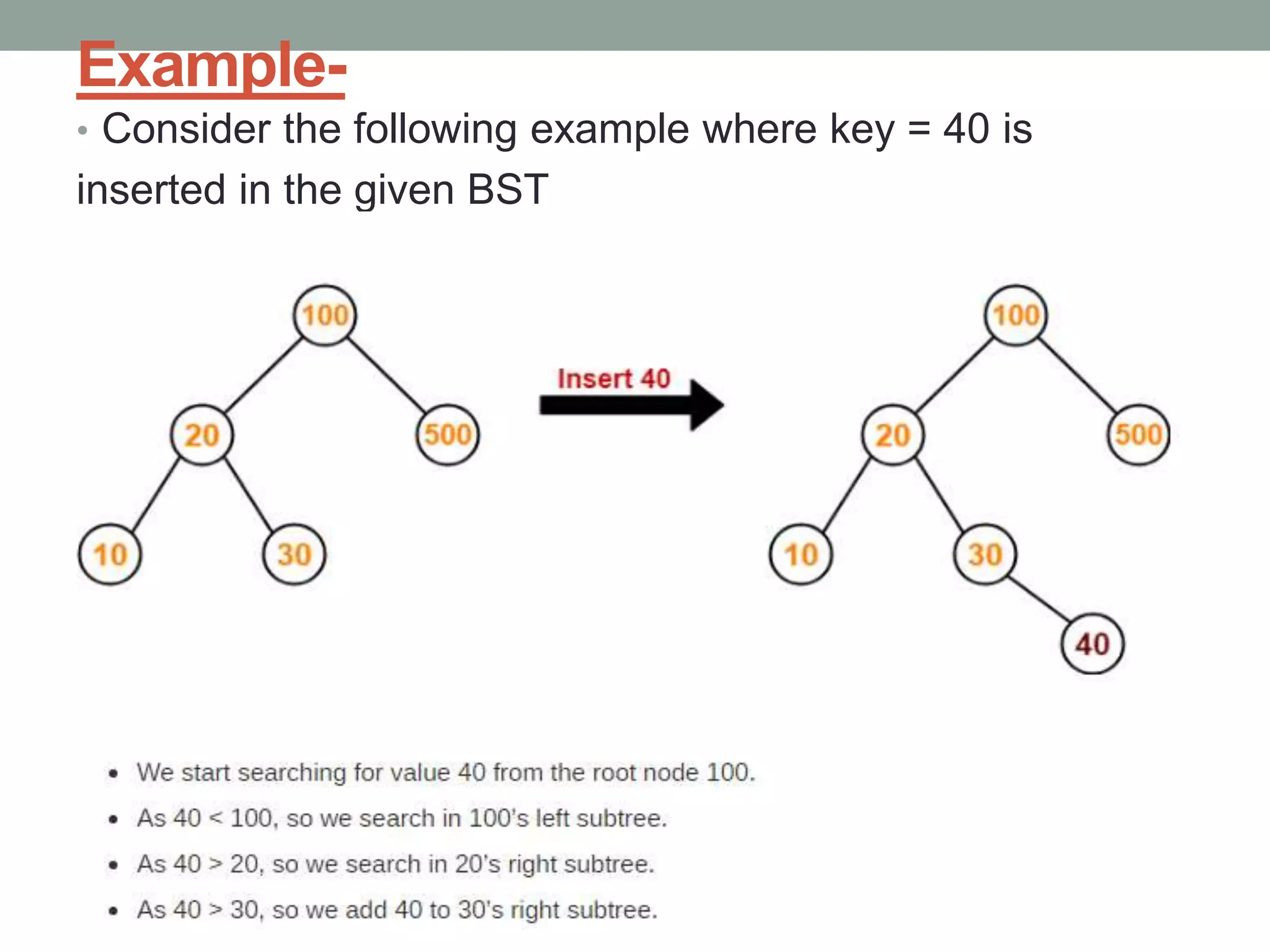
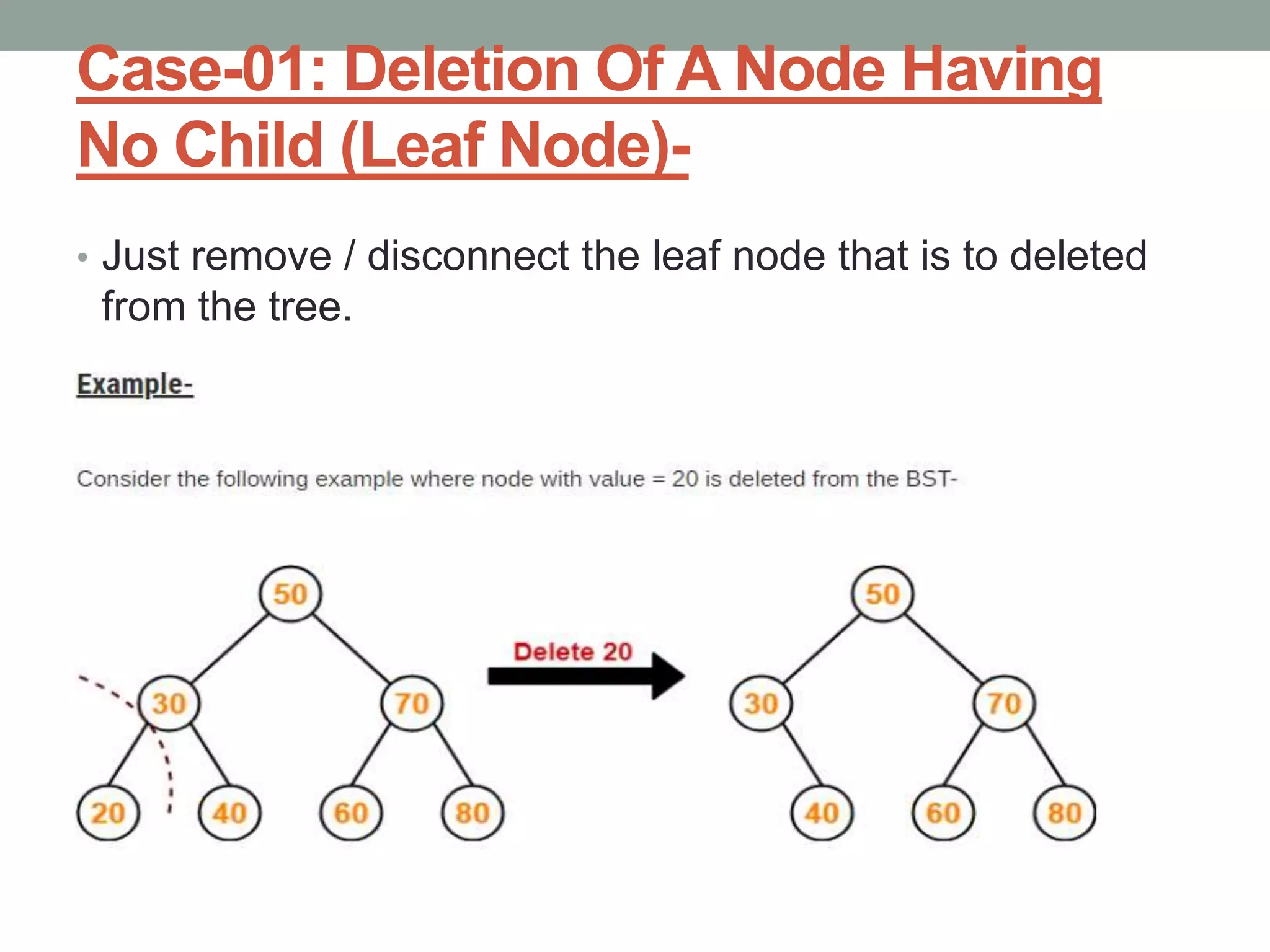
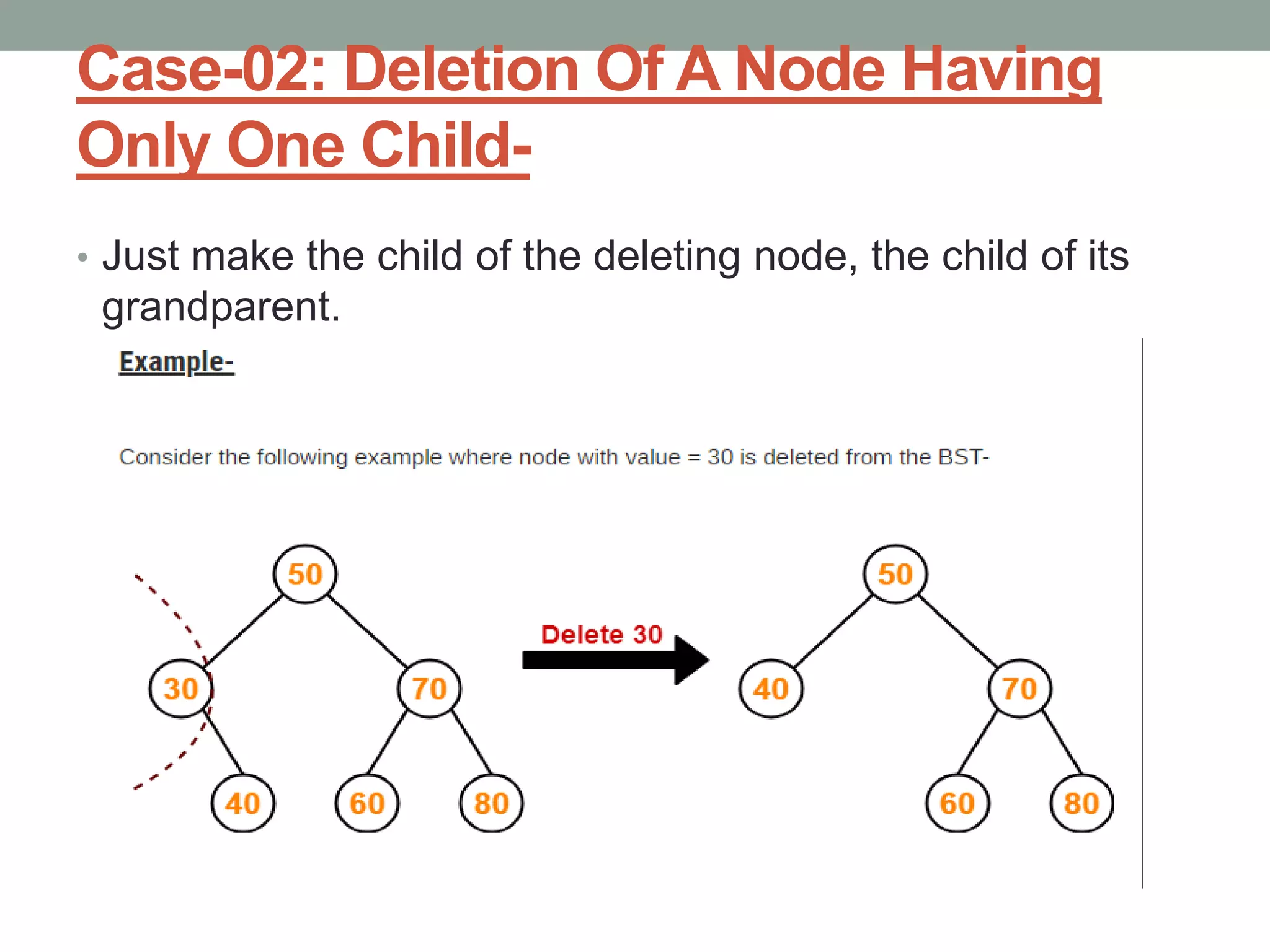
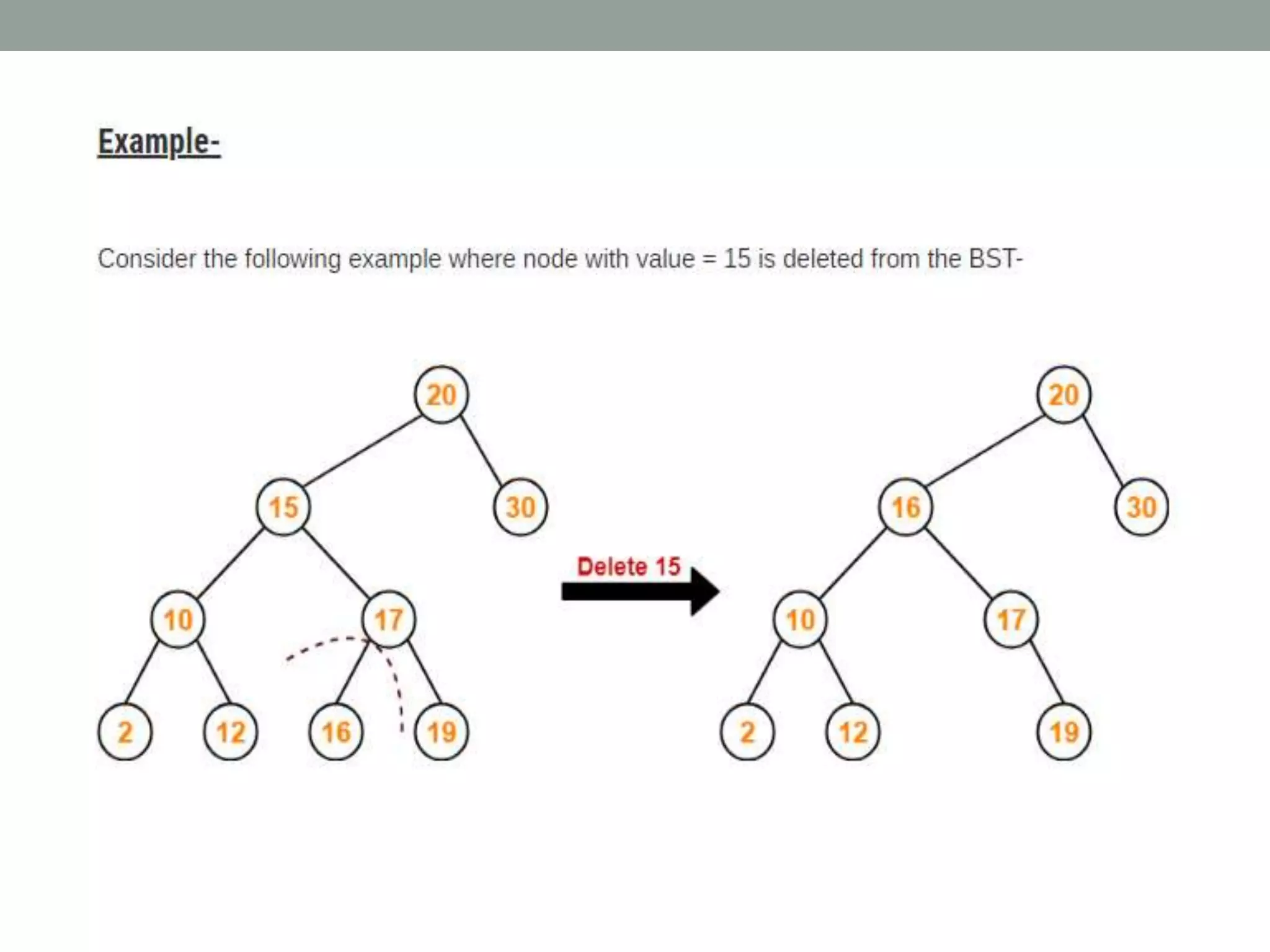
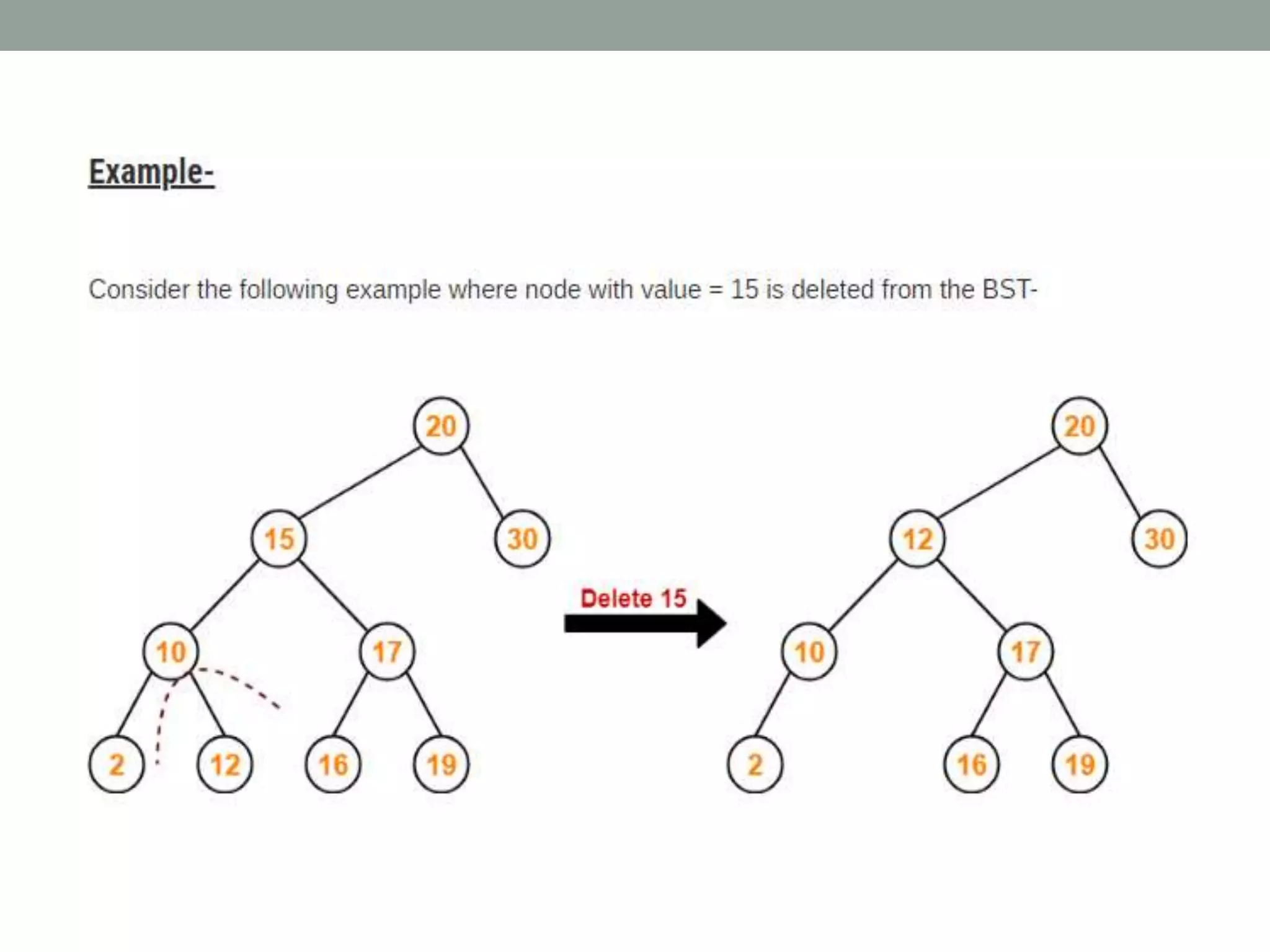
Tree representations can be list-based or use left child and right sibling pointers. Binary search trees store values such that all left descendants are less than the node value and all right descendants are greater. Common operations on binary search trees are search, insertion, and deletion through comparing node values, replacing nodes, or restructuring subtrees.

1. TREE
REPRESENTATION

2. Tree Representation
• It can be represented in two methods
• List Representation
• Left Child - Right Sibling Representation

3. List Representation
• In this representation, two types of nodes are used
• Representing the node with data called 'data node' and
• Representing only references called 'reference node'.
• Start with a 'data node' from the root node in the tree.
• Then it is linked to an internal node through a 'reference node'
which is further linked to any other node directly.
• This process repeats for all the nodes in the tree.

4. Example of list representation

5. Left Child - Right Sibling Representation
• In this representation, a list with one type of node which
consists of three fields namely
• Data field,
• Left child reference field and
• Right sibling reference field.
• Data field stores the actual value of a node.
• Left reference field stores the address of the left child
otherwise NULL and
• Right reference field stores the address of the right sibling
node otherwise NULL.

6. Graphical representation of that node is
as follows...

7. Binary Tree Data structure
• A tree in which every node can have a maximum of
two children is called Binary Tree.
• In a binary tree, every node can have either 0 children or
1 child or 2 children but not more than 2 children.

8. Types of Binary Trees
• Strictly binary tree
• Complete binary tree
• Extended binary tree.

9. Strictly Binary Tree
• In a binary tree, every node can have a maximum of two
children.
• But in strictly binary tree, every node should have exactly
two children or none (i.e) every internal node must have
exactly two children. A strictly Binary Tree can be defined
as follows...
• Strictly binary tree is also called as Full Binary Tree or
Proper Binary Tree or 2-Tree

10. Example

11. Complete Binary Tree
• In a binary tree, every node can have a maximum of two
children.
• But in strictly binary tree, every node should have exactly two
children or none and
• In complete binary tree all the nodes must have exactly two
children and at every level of complete binary tree there must
be 2level number of nodes.
• For example at level 2 there must be 22 = 4 nodes and at level
3 there must be 23 = 8 nodes.
• A binary tree in which every internal node has exactly two
children and all leaf nodes are at same level is called
Complete Binary Tree.
• Complete binary tree is also called as Perfect Binary Tree.

12. Example

13. Extended Binary Tree
• The full binary tree obtained by adding dummy nodes to a
binary tree is called as Extended Binary Tree.

14. Binary Tree Representations
• A binary tree data structure is represented using two
methods. Those methods are as follows...
• Array Representation
• Linked List Representation

15. Array Representation of Binary Tree
• In array representation of a binary tree, we use one-
dimensional array (1-D Array) to represent a binary tree.
• To represent a binary tree of depth 'n' using array
representation, need one dimensional array with a
maximum size of 2n + 1.

16. Linked List Representation of Binary
Tree
• Use a doubly linked list to represent a binary tree.
• In a doubly linked list, every node consists of three fields.
• First field for storing left child address
• Second for storing actual data and
• Third for storing right child address.

18. Binary Tree Traversals
• To display a binary tree, need to follow some order in
which all the nodes of that binary tree must be displayed.
• In any binary tree, displaying order of nodes depends on
the traversal method.
• Displaying (or) visiting order of nodes in a binary tree
is called as Binary Tree Traversal.

19. Types of binary tree traversals
• There are three types of binary tree traversals.
• In - Order Traversal
• Pre - Order Traversal
• Post - Order Traversal

20. In - Order Traversal ( left Child - root –
right Child )
• In-Order traversal, the root node is
visited between the left child and right
child.
• In this traversal, the left child node is
visited first, then the root node is
visited and later visiting the right child
node.
• This in-order traversal is applicable
for every root node of all sub-trees in
the tree.
• This is performed recursively for all
nodes in the tree.
I - D - J - B - F - A - G - K - C - H

22. Pre - Order Traversal ( root – left Child
– right Child )
• Pre-Order traversal, the root
node is visited before the left
child and right child nodes.
• In this traversal, the root node is
visited first, then its left child and
later its right child.
• This pre-order traversal is
applicable for every root node of
all sub-trees in the tree.
A - B - D - I - J - F - C - G - K - H

24. Post - Order Traversal ( left Child –
right Child - root )
• In Post-Order traversal, the root
node is visited after left child and
right child. In this traversal, left
child node is visited first, then its
right child and then its root node.
• This is recursively performed until
the right most node is visited.
I - J - D - F - B - K - G - H - C - A

26. Example 1

27. Answers
• (a) Inorder (Left, Root, Right) : 4 2 5 1 3
(b) Preorder (Root, Left, Right) : 1 2 4 5 3
(c) Postorder (Left, Right, Root) : 4 5 2 3 1

28. Example 2

29. • Preorder = A B D C E G F H I.
• Inorder = B D A G E C H F I.
• Postorder = D B G E H I F C A.

30. Example 3

32. Example 4

33. Answer

34. Example 5

39. BINARY SEARCH TREE

40. Introduction
• Binary Search Tree is a binary tree in which every node
contains only smaller values in its left subtree and only
larger values in its right subtree.

41. Example
• Construct a Binary Search Tree by inserting the following
sequence of numbers...
10,12,5,4,20,8,7,15 and 13

44. Binary Search Tree
• Binary Search tree is a binary Tree with following
properties:
• Left sub tree of a node always contains lesser key
• Right sub tree of a node always contains greater key
• Equal valued keys are not allowed

45. Binary Search Tree Operations
• Commonly performed operations on binary search tree
are-

46. Search Operation-
• Search Operation is performed to search a particular
element in the Binary Search Tree.
• Rules-
• For searching a given key in the BST,
• Compare the key with the value of root node.
• If the key is present at the root node, then return the root
node.
• If the key is greater than the root node value, then recur
for the root node’s right subtree.
• If the key is smaller than the root node value, then recur
for the root node’s left subtree.

47. Example-
• Consider key = 45 has to be searched in the given BST

48. • We start our search from the root node 25.
• As 45 > 25, so we search in 25’s right subtree.
• As 45 < 50, so we search in 50’s left subtree.
• As 45 > 35, so we search in 35’s right subtree.
• As 45 > 44, so we search in 44’s right subtree but 44 has
no subtrees.
• So, we conclude that 45 is not present in the above BST.

49. Insertion Operation-
• Insertion Operation is performed to insert an element in
the Binary Search Tree.
• Rules-
• The insertion of a new key always takes place as the child
of some leaf node.
• For finding out the suitable leaf node,
• Search the key to be inserted from the root node till some
leaf node is reached.
• Once a leaf node is reached, insert the key as child of that
leaf node.

50. Example-
• Consider the following example where key = 40 is
inserted in the given BST

51. Deletion Operation
• Deletion Operation is performed to delete a particular
element from the Binary Search Tree.
• When it comes to deleting a node from the binary search
tree, following three cases are possible
• Case-01: Deletion Of A Node Having No Child (Leaf
Node)-
• Case-02: Deletion Of A Node Having Only One Child-
• Case-03: Deletion Of A Node Having Two Children-

52. Case-01: Deletion Of A Node Having
No Child (Leaf Node)-
• Just remove / disconnect the leaf node that is to deleted
from the tree.

53. Case-02: Deletion Of A Node Having
Only One Child-
• Just make the child of the deleting node, the child of its
grandparent.

54. Case-02: Deletion Of A Node Having
Two Children-
• A node with two children may be deleted from the BST in
the following two ways-
• Method-01:
• Visit to the right sub tree of the deleting node.
• Pluck the least value element called as in-order
successor.
• Replace the deleting element with its in-order successor.

56. • Method-02:
• Visit to the left sub-tree of the deleting node.
• Pluck the greatest value element called as in-order
predecessor.
• Replace the deleting element with its in-order
predecessor.