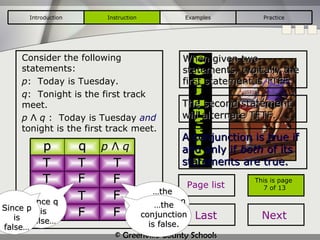
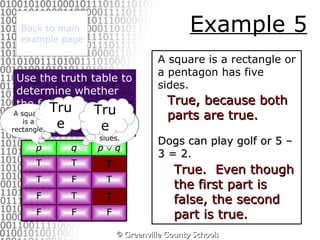
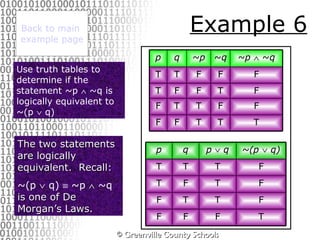
This document provides an introduction to symbolic logic, including simple and compound statements, logical connectives such as NOT, AND and OR, and truth tables. It defines statements, connectives, negation, conjunction, disjunction and uses truth tables to evaluate logical statements. Examples are provided to illustrate logical concepts like negation, conjunction, disjunction and logically equivalent statements using truth tables.

1. Introduction to Logic Simple and Compound Statements Connectives NOT, AND, OR Resources: HRW Geometry, Lesson 12.2

2. How can you tell when a complicated statement is true or false? In the nineteenth century, George Boole symbolic logic . He believed logical ideas could be calculated symbolically. His methods allow us to perform calculations to decide if statements are true or false and whether logical arguments are valid. Introduction Instruction Examples Practice

3. Please go back or choose a topic from above. Introduction Instruction Examples Practice

6. Identify which of the following sentences are “statements” as defined in logic. YES NO YES NO YES YES NO Kimberly lives in Cebu City. Drop that puppy right now! My pencil is broken. Do we have an assignment for today? The Philippines has more than 8 000 islands. The complement of 50° is 40°. Please hand me my bag. Is this a logical “statement”?

7. A Compound Statement A simple statement contains a single idea. A Simple Statement “ The 1998 Yankees were the best team in the history of baseball.” A compound statement contains several ideas combined together. If you break your lease, then you forfeit your deposit. Introduction to Symbolic Logic Introduction Instruction Examples Practice This is page 2 of 13 Page list Last Next

8. Words used to join the ideas of a compound statement are called connectives. Three of the connectives are not , and , and or . This is page 3 of 13 The Symbols Page list Last Next Introduction Instruction Examples Practice NOT ~ AND OR Negation NOT Conjunction AND Disjunction OR

9. A negation is a statement expressing the idea that something is not true. We represent negation by the symbol ~ and use the word “ not ” . If p represents “The blue whale is the largest living creature,” then ~p represents “The blue whale is not the largest living creature.” The Connectives - Negation Introduction Instruction Examples Practice This is page 4 of 13 Page list Last Next

10. Consider the following statements: p : The sun is a star. ~ p : The sun is not a star. When the first statement, p , is true, the second statement, ~p, is false, and vice versa. We can represent this in a truth table . Graphic Page list Negation This is where the symbol that represents your first statement will go. This is where the symbol that represents your second statement will go. Since the first entry is true, the second entry is false. Since we are looking at the negation of the statement, here we need the opposite of the previous column p T F ~p F T By convention this first entry is usually TRUE. Introduction Instruction Examples Practice This is page 5 of 13 Last Next

11. Give the truth value of the given statements, its negation and the negation’s truth value. Statement Truth Value Negation The penguin is classified as a bird. T The penguin is not classified as a bird. F Truth Value The Philippine flag has five colors. F The Philippine flag does not have five colors. T The difference of 38 and 13 is not equal to 25. F The difference of 38 and 13 is equal to 25. T Mars is not the hottest planet in the solar system. T Mars is the hottest planet in the solar system. F Two points are always collinear. T Two points are not always collinear. F Two planes does not intersect at a point. T Two planes intersect at a point. F

12. A conjunction expresses the idea of and . We use the symbol Λ to represent a conjunction. p : d : p Λ d : ~p Λ ~d : Now write the conjunction of the negations of each statement: NOT p and NOT d Now write the conjunction of the two statements: p and d Jovie is not a good dancer and Noel is not a superb artist. Jovie is a good dancer and Noel is a superb artist. This will be your second statement. This will be your first statement. Noel is a superb artist. Jovie is a good dancer. Next The Connectives - Conjunction Introduction Instruction Examples Practice This is page 6 of 13 Page list Last

13. Consider the following statements: p : Today is Tuesday. q : Tonight is the first track meet. p Λ q : Today is Tuesday and tonight is the first track meet. Conjunction T T T T T F F F F F F F p q p Λ q When given two statements, typically the first statement is TTFF. The second statement will alternate TFTF. A conjunction is true if and only if both of its statements are true. Introduction Instruction Examples Practice This is page 7 of 13 Page list Last Next Since q is false… … the conjunction is false. Since p is false… … the conjunction is false.

15. A disjunction conveys the notion of or . We use the symbol V to represent a disjunction. The Connectives u : Human population will increase. c : Raw resources will be depleted. u V c : Human population will increase or raw resources will be depleted. ~u V c : Human population will not increase or raw resources will be depleted. Introduction Instruction Examples Practice This is page 8 of 13 Page list Last Next

16. In everyday life, “or” means one or the other but not both. This is called the exclusive or. In logic, “or” means one or the other or both, called the inclusive or. Disjunction A disjunction is false if and only if both of its statements are false. This statement is false only if John does neither. T T T F He goes swimming…. … so the disjunction is true. He goes bowling…. … so the disjunction is true. He does BOTH so the disjunction is TRUE. He does NEITHER so the disjunction is FALSE. Introduction Instruction Examples Practice This is page 9 of 13 Page list Last Next p q p  q T T T F F T F F

18. This is page 10 of 13 Page list Last Next Negation “NOT” ~ Truth value is the opposite of the original statement Conjunction “AND” Λ Truth value of a conjunction is true ONLY if both statements are true Disjunction “OR” V Truth value of a disjunction is false ONLY if both statements are false Introduction Instruction Examples Practice

22. Complete the following truth table to negate a conjunction. Truth Tables – The Negation of a Conjunction A conjunction is only true if both statements are true A negation yields the opposite of the previous statement. Click to see the solution. Introduction Instruction Examples Practice This is page 11 of 13 Page list Last Next p q p  q ~(p  q) T T T F F T F F p q p  q ~(p  q) T T T F T F F T F T F T F F F T

23. This is page 12 of 13 Page list Last Next Complete the following truth table for the disjunctions of two negations. Truth Tables – The Disjunction of Two Negations Click for the solution. Introduction Instruction Examples Practice p q ~p ~q ~p V ~ q T T F F F T F F T T F T T F T F F T T T p q ~p ~q ~p V ~ q T T T F F T F F

24. Compare the last columns of the two truth tables. Truth Tables – Logically Equivalent Statements and DeMorgan’s Law When two statements have the same truth values they are said to be logically equivalent (  ) . Therefore, ~(p  q)  ~p  ~ q This is one of DeMorgan’s Laws. Introduction Instruction Examples Practice This is page 13 of 13 Page list Last Next p q ~p ~q ~p  ~ q T T F F F T F F T T F T T F T F F T T T p q p  q ~(p  q) T T T F T F F T F T F T F F F T

25. You have now completed the instructional portion of this lesson. You may proceed to more examples or the practice assignment. Introduction Instruction Examples Practice

27. Please go back or choose a topic from above. Introduction Instruction Examples Practice

28. Practice How complicated can truth tables be? Practice Logic Tables Click on address below to practice truth tables Introduction Instruction Examples Practice

29. Please go back or choose a topic from above. Introduction Instruction Examples Practice

30. Example 1 The Braves won last night. Back to main example page Identify each sentence as simple or compound. SIMPLE Phil played the guitar and sang. COMPOUND Sherri talked on the phone or played bridge all evening. COMPOUND Dan is not mad at me. COMPOUND Only one idea Two ideas… conjunction Two ideas… disjunction Negation

31. q    r Example 2 p Back to main example page Express each of the symbolic statements in words. p = “You like to paint,” q = “You are an artist,” r = “You draw landscapes.” You like to paint ~r You don’t like to draw landscapes ~p You don’t like to paint   q and you are not an artist.  p or you like to paint. or you are an artist and you don’t draw landscapes.

32. Example 3 I am not angry at you! Back to main example page Write the negation of each statement. I am angry at you! My best friend is coming over tonight. My best friend is not coming over tonight. The polygon is a not a regular polygon. The polygon is a regular polygon. not

33. Example 4 George Washington was the first president of the U.S. and John Adams was the second. Back to main example page Use the truth table to determine whether the following conjunctions are true or false. True, because both parts are true. The sum of the measures of the angles of a pentagon is 720° and red is a color. False. Even though the second part is true, the first part is false. George Washington was the first president. John Adams was the second president. True The sum of pentagon’s angles is 720 o . True T False Red is a color. True F p q p Λ q T T T T F F F T F F F F

34. Use the truth table to determine whether the following disjunctions are true or false. False True 5 - 3 = 2 Dogs can play golf. Example 5 A square is a rectangle or a pentagon has five sides. Back to main example page True, because both parts are true. Dogs can play golf or 5 – 3 = 2. True. Even though the first part is false, the second part is true. A square is a rectangle. A pentagon has five sides. True True T T p q p  q T T T T F T F T T F F F

35. Example 6 Back to main example page Use truth tables to determine if the statement ~p  ~q is logically equivalent to ~(p  q) The two statements are logically equivalent. Recall: ~(p  q)  ~p  ~q is one of De Morgan’s Laws. p q p  q ~(p  q) T T T F T F T F F T T F F F F T p q ~p ~q ~p  ~ q T T F F F T F F T F F T T F F F F T T T