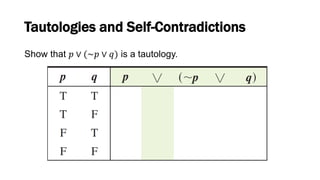
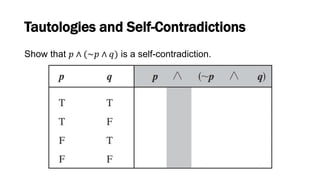
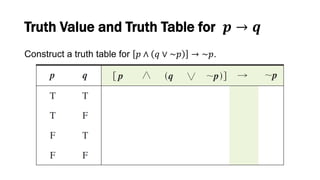
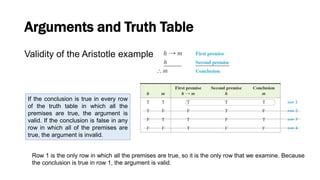
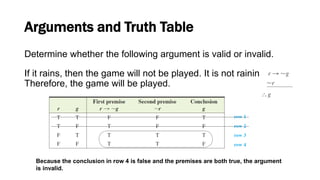
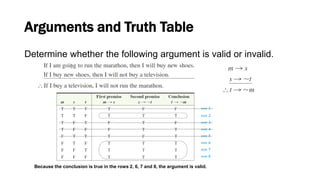
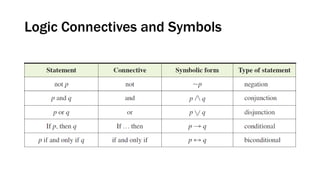
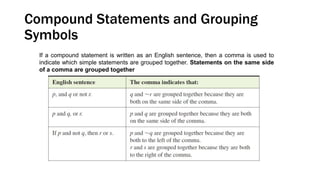
This document discusses elementary logic concepts such as statements, truth tables, and logical connectives. It begins by defining a statement as a declarative sentence that is either true or false. Examples of different types of sentences like questions and commands are provided. The rest of the document explores logical concepts like simple and compound statements, truth tables, logical connectives like conjunction and negation, conditional and biconditional statements, and identifying tautologies and contradictions. Practice problems are included throughout for the reader.













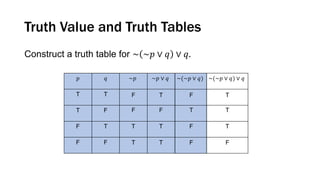
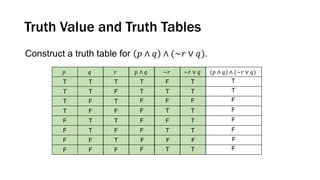
![Truth Tables (via Order of Precedence)
Construct a truth table for 𝑝 ∨ [~ 𝑝 ∧ ~𝑞 ].](https://image.slidesharecdn.com/1-220917072338-0c496726/85/1-Logic-pptx-18-320.jpg)