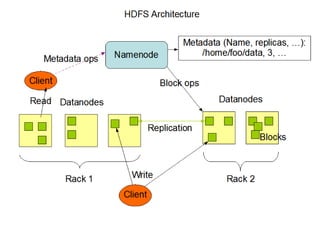
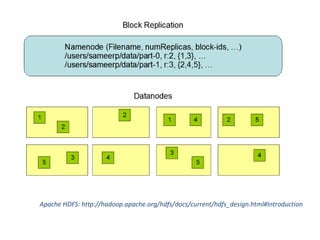
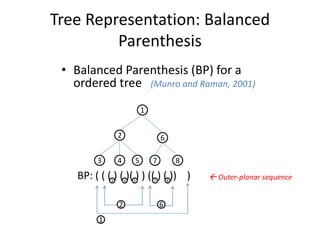
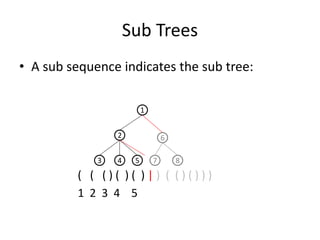
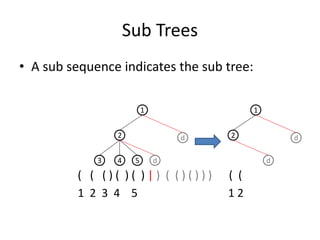
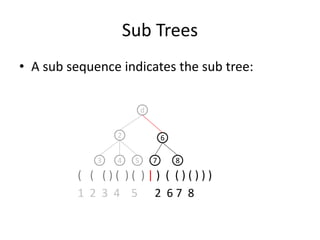
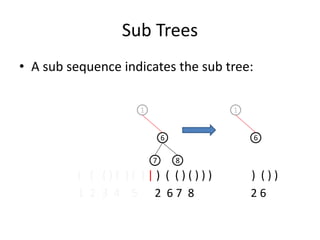
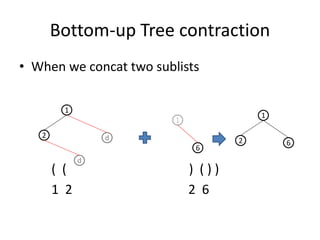
The document discusses the representation of tree structures within the MapReduce framework using a balanced parenthesis (bp) scheme. It outlines how files are divided, metadata management in a distributed file system, and methods for tree contraction and subtree representation. Additionally, it touches on practical applications such as XML transformation and hierarchical clustering algorithms within MapReduce.

1. Tree Representation in
MapReduce World
IPL weekly-seminar
Yu Liu@NII
2011-11-22

2. Distributed File System of MapReduce
• A GFS/HDFS cluster consists of a single master
(namenode) and multiple chunkservers (datanodes)
and is accessed by multiple clients.
• The master maintains all filesystem metadata.
• Clients interact with the master for metadata
operations, but all data-bearing communication goes
directly to the datanodes

4. Distributed File System of MapReduce
• Architecture of GFS/HDFS
– Files are divided into fixed-size chunks
– Each chunk is identified by an immutable and
globally unique 64 bit integer (chunk handle)
– Each chunk is replicated on multiple chunkservers
– Chunks of a file are placed as balance as possable
in the cluster.
(The Google File System, SOSP03)

5. Apache HDFS: http://hadoop.apache.org/hdfs/docs/current/hdfs_design.html#Introduction

6. Inputs and Outputs of MapReduce
• The MapReduce framework operates exclusively on
<key, value> pairs.
• Each pair is called a record.
• Applications specify the input/output locations and
supply map and reduce functions and other job
parameters, comprise the job configuration. The job
client then submits the job to framework.

7. Tree Data Structure inside MapReduce
• Currently, GFS/HDFS prefers flat data
structures/ files, files such as xml is not
supported.
• We already know how to represent a file
which contains a large list in HDFS (EuroPar
2011)
• Tree representation is still a problem.

8. How to Represent a Tree in
MapReduce
• If we can represent the tree by an list , and if :
When this list is split into arbitrary continues sublists,
each split of the list represents a sub tree
After any tree contracting operations on each sub tree,
concated sublists can still get a tree
Then such a list is what we want.

9. Tree Representation: Balanced
Parenthesis
• Balanced Parenthesis (BP) for a
ordered tree (Munro and Raman, 2001)
BP: ( ( ( ) ( )( ) ) (( ) ( )) )
1
2 6
73 4 5 8
1
2 6
3 4 5 7 8
 Outer-planar sequence

10. BP Can Be A Solution
• A tree node can be represented by a pair of
parentheses :
• node= ( ‘(’ , ‘)’ )
• We want to represent a list of nodes, the nodes
should be sort-able
• data HalfNode = HalfNode{lr::Char, id::Int, index::Int}
– E.g.: left1 : HalfNode {lr=‘L’, id=1 , index=0} ,
right1 : HalfNode {lr=‘R’, id=1 , index=16}
• data Node = Node { left::HalfNode, right::HalfNode}
– E.g. : the root ① : Node {left =left1, right =right1 }

11. Parenthesis / HalfNode
• For simple we define
data HalfNode = (Bool,Int,Int)
leftPar: (False, _,_)
rightPar: (True, _,_)
so that a node can be expressed by two HalfNodes,
E.g.: the root ① : { (False, 1 , 0) , (True, 1, 15) }
the node ②: {(False, 2 , 1) , (True, 2, 7) }
the node ⑦: {(False, 7 , 10) , (True, 7, 11) }

12. Comparable HalfNode
• A set of HalfNode can be sorted by index to get a BP
sequence
– data HalfNode = (Bool,Int,Int)
– We know each bracket is left or right
• { (False, 1 , 0) , (False, 2 , 1) , (False, 3, 2)
(True, 3 , 3) , (False, 4 , 4) , (True, 4 , 5)
(False, 5 , 6) , (True, 5 , 7) , (True, 2 , 8)
(False, 6 , 9) , (False, 7 , 10) , (True, 7 , 11)
(False, 8 , 12), (True, 8 , 13) , (True, 6 , 14)
(True, 1 , 15)}

13. Sub Trees
• A sub sequence indicates the sub tree:
( ( ( ) ( ) ( ) | ) ( ( ) ( ) ) )
1 2 3 4 5
1
2 6
73 4 5 8

14. Sub Trees
• A sub sequence indicates the sub tree:
( ( ( ) ( ) ( ) | ) ( ( ) ( ) ) ) ( (
1 2 3 4 5 1 2
1
2 d
d3 4 5
1
2 d
d

15. Sub Trees
• A sub sequence indicates the sub tree:
( ( ( ) ( ) ( ) | ) ( ( ) ( ) ) )
1 2 3 4 5 2 6 7 8
d
2 6
73 4 5 8

16. Sub Trees
• A sub sequence indicates the sub tree:
( ( ( ) ( ) ( ) | ) ( ( ) ( ) ) ) ) ( ) )
1 2 3 4 5 2 6 7 8 2 6
1
6
7 8
1
6

17. Bottom-up Tree contraction
• When we concat two sublists
( ( ) ( ) )
1 2 2 6
1
2 d
d
1
6
1
2 6

18. Sub Trees
• { (False, 1 , 0) , (False, 2 , 1) , (False, 3, 2)
(True, 3 , 3) , (False, 4 , 4) , (True, 4 , 5)
(False, 5 , 6) , (True, 5 , 7) , (True, 2 , 8)
(False, 6 , 9) , (False, 7 , 10) , (True, 7 , 11)
(False, 8 , 12), (True, 8 , 13) , (True, 6 , 14)
(True, 1 , 15)}

19. Splitting and Grouping
• We can split a list and group the elements of
each sub-list in MapReduce.
– We extend data HalfNode = (Bool,Int, (Int, Int) )
• Here (Int, Int) is the index /d and index
• For the BP-MR sequence, that means we can
split a tree by number of brackets

20. Practical Data
• Real data are associated to left-half-node
– data HalfNode = ((Int, Int), Bool, Int, Map)
– For right-half-nodes, let Map be always
empty/null

21. Bottom-up Build a Tree
• A list a items as input
• Make a sparse list of “leaf”:
E.g.: [ ((0,100),False, 100, data1), ((0,101), True, 100,
null) , ( (0, 200), False, 200, data2), ( (0, 201), True, 200,
data2) .. ]
( 100) (200) (300) (400) ….
• Insert parents
( ( 100) (200) ) ( (300) (400) )….
50 250

22. Examples
• XML
– XML file is just a BP representation
An example of a xml file:
<?xml version="1.0"?>
<note>
<to>Tove</to>
<from>Jani</from>
<heading>Reminder</heading>
<body>Don't forget </body>
</note>

23. Examples
• XML file can be easily transformed to BP-MR
– Operation:
• query
– by xpath
– By id / index
• Parallel parsing ?

24. Hieratical Clustering
• This work is not finished
• Usually, clustering algorithms are related to
two categories: hierarchical and partitioning
• The more popular hierarchical agglomerative
clustering (HAC) algorithms use a bottom-up
approach to merge items into a hierarchy of
clusters.

25. Hieratical Clustering

26. Hieratical Clustering
• The Average-link is one of the most popular
algorithms for hieratical clustering
• Average link: The distance between any two
clusters is the average distance between each
pair of points such that each pair has a point
in both clusters

27. GTA Algorithm for Hieratical Clustering
Currently only for the first merge step
• Initial data are a set of items
• map makeNode items
where makeNode item= ((0,0), False, 1, item ) , ((0,0), True, 1,
item )
• Input are a BP-MR sequence but only left-half
• Generate: all possible bags
• Test: only keep pairs
• Aggregate : the minimum distance pair
• Post-process : new HalfNode pair which is parent
of aggregate’s results

28. Problems
• Hard to do insertion
– Appending to the tail is easy but insertion into
other place is difficult
• Parallel generate BP-MR sequences
– Ideas: first generate skeletons of a tree

29. Skeletons of a Tree
• For example
a = 1000, b = 2000, c= 3000 …
Index_a = 1000, index_b=2000, index_c = 3000 …
Index_a’ = 8000, index_b’ = 4000, index_c’ = 6000 …
1
a e
fb c d g

30. End
• Thanks