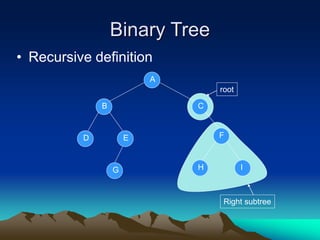
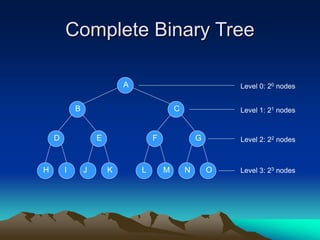
The document discusses various tree data structures, including binary trees and binary search trees. It provides definitions and examples of binary trees, their terminology like root, left/right subtrees, and tree traversal methods including preorder, inorder and postorder. It also discusses applications of binary search trees for searching, as well as operations on trees like inserting, deleting and traversing nodes.